Giải Toán 10 (Chân trời sáng tạo): Bài tập cuối chương 1

Giải bài tập Toán 10 Bài tập cuối chương 1

Video giải bài tập Toán 10 Bài tập cuối chương 1

Bài tập

Giải Toán 10 trang 27 Tập 1

Bài 1 trang 27 Toán lớp 10 Tập 1: Xác định tính đúng sai của mỗi mệnh đề sau:

a) {a} ∈ {a; b; c; d};

b) ∅ = {0};

c) {a; b; c; d} = {b; a; d; c};

d) {a; b; c} $\not\subset$ {a; b; c}.

Lời giải:

a) Mệnh đề (a) sai vì,{a} là tập hợp và là tập con của tập hợp {a; b; c; d} nên ta viết {a} $\subset$ {a; b; c; d}.

b) Mệnh đề (b) sai vì, tập rỗng là tập không có phần tử nào nên $\varnothing$ ≠ {0};

c) Mệnh đề (c) đúng vì, tập {a; b; c; d} $\subset$ {b; a; d; c} và {b; a; d; c} $\subset${a; b; c; d} nên {a; b; c; d} = {b; a; d; c};

d) Mệnh đề (d) sai vì, các phần tử của tập {a; b; c} đều thuộc tập {a; b; c} nên {a; b; c}$\subset${a; b; c}

Bài 2 trang 27 Toán lớp 10 Tập 1: Xét tính đúng sai của mỗi mệnh đề sau:

a) Nếu 2a – 1 > 0 thì a > 0 (a là số thực cho trước);

b) a – 2 > b nếu và chỉ nếu a > b + 2 (a, b là hai số thực cho trước).

Lời giải:

a) Mệnh đề (a) đúng vì nếu 2a > 1 thì a > $\frac{1}{2}$ nên a > 0.

b) Mệnh đề (b) đúng vì, a – 2 > b $\iff$ a > b + 2 (theo tính chất của bất phương trình)

Bài 3 trang 27 Toán lớp 10 Tập 1: Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ”, phát biểu lại các định lí sau:

a) Nếu B ⊂ A thì A ∪ B = A (A, B là hai tập hợp);

b) Nếu hình bình hành ABCD có hai đường chéo vuông góc với nhau thì nó là hình thoi.

Lời giải:

a) Sử dụng thuật ngữ “điều kiện cần”:

“Để B $\subset$ A thì điều kiện cần là A$\cup$B = A (A, B là hai tập hợp)”

Sử dụng thuật ngữ “điều kiện đủ”:

“Để A$\cup$B = A thì điều kiện đủ là B $\subset$ A(A, B là hai tập hợp)”

b) sử dụng thuật ngữ “điều kiện cần”.

“Để hình bình hành ABCD có hai đường chéo vuông góc với nhau thì điều kiện cần là hinh bình hành ABCD là hình thoi”.

Sử dụng thuật ngữ “điều kiện đủ”

“Để hình bình hành ABCD là hình thoi thì điều kiện đủ là hình bình hành ABCD có hai đường chéo vuông góc với nhau”.

Bài 4 trang 27 Toán lớp 10 Tập 1: Cho định lí “∀x ∈ ℝ, x ∈ ℤ nếu và chỉ nếu x + 1 ∈ ℤ”. Phát biểu lại định lí này, sử dụng thuật ngữ “điều kiện cần và đủ”.

Lời giải:

Định lí trên được phát biểu như sau: “Với $\forall x\in ℝ$ để $x\in \mathbb{Z}$ thì điều kiện cần và đủ là x + 1 $\in$ ℤ”

Bài 5 trang 27 Toán lớp 10 Tập 1: Xét tính đúng sai của các mệnh đề sau:

a) ∀x ∈ ℕ , x³ > x;

b) ∀x ∈ ℤ, x ∉ ℕ;

c) ∀x ∈ ℝ, nếu x ∈ ℤ thì x ∈ $\mathbb{Q}$ .

Lời giải:

a) Mệnh đề “$\forall x\in \mathbb{N}$, x³ > x” là mệnh đề sai vì, tồn tại x = 0 $\in \mathbb{N}$để 0³ = 0.

b) Mệnh đề $\exists x\in \mathbb{Z},x\notin \mathbb{N}$ là mệnh đề đúng vì, tồn tại x = - 2 $\in \mathbb{Z}$ nhưng x = - 2 $\notin \mathbb{N}$.

c) Mệnh đề $\forall x\in ℝ$ nếu $x\in \mathbb{Z}$ thì $x\in \mathbb{Q}$ là mệnh đề đúng vì, tập ℤ$\subset$ℚ nên với $\forall x\in \mathbb{Z}$ thì $x\in \mathbb{Q}$.

Bài 6 trang 27 Toán lớp 10 Tập 1: Xét các quan hệ bao hàm giữa các tập hợp dưới đây. Vẽ biểu đồ Ven để thể hiện các quan hệ bao hàm đó.

A là tập hợp các hình tứ giác;

B là tập hợp các hình bình hành;

C là tập hợp các hình chữ nhật;

D là tập hợp các hình vuông;

E là tập hợp các hình thoi

Lời giải:

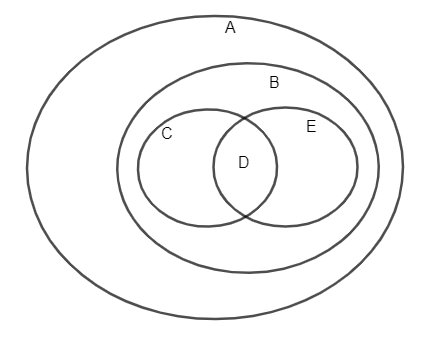
Hình vuông là hình thoi và cũng là hình chữ nhật nên D là giao của tập C và tập E.

Hình thoi và hình chữ nhật là hình bình hành (vì có các cặp cạnh đối song song) nên tập C và E là tập con của tập B.

Hình bình hành là tứ giác (vì có 4 cạnh) nên tập B là tập con của tập A.

Ta có biểu đồ ven thể hiện các mối quan hệ bao hàm như sau:

Bài 7 trang 27 Toán lớp 10 Tập 1: a) Hãy viết tất cả các tập con của tập hợp A = {a; b; c}.

b) Tìm tất cả các tập hợp B thỏa mãn điều kiện {a; b} ⊂ B ⊂ {a; b; c; d}.

Lời giải:

a) Các tập con của tập hợp A là: {a}; {b}; {c}; {a;b}; {a; c}; {b; c}; {a; b; c}; $\varnothing$.

Vậy các tập con của tập A là {a}; {b}; {c}; {a;b}; {a; c}; {b; c}; {a; b; c}; $\varnothing$.

b) Các tập hợp B thỏa mãn điều kiện {a; b} $\subset$ B $\subset${a; b; c; d} là:

B = {a; b} hoặc B = {a; b; c} hoặc B = {a; b; d} hoặc B = {a; b; c; d}.

Vậy tất cả các tập hợp B thỏa mãn điều kiện đã cho là: B = {a; b}, B = {a; b; c}, B = {a; b; d}, B = {a; b; c; d}.

Bài 8 trang 27 Toán lớp 10 Tập 1: Cho A = {x ∈ ℝ |x² – 5x – 6 = 0}, B = {x ∈ ℝ |x² = 1}. Tìm A∩B, A∪B, A\B, B\A.

Lời giải:

Phương trình x² – 5x – 6 = 0 có hai nghiệm x = -1 và x = 6 đều là các số thực.

⇒ A = {- 1; 6}.

Phương trình x² = 1 có hai nghiệm x = 1 và x = -1 đều là các số thực.

⇒ B = {- 1; 1}.

Khi đó, các tập hợp được xác định như sau:

A$\cap$B = {- 1};

A$\cup$B = {- 1; 1; 6};

A\B = {6};

B\A = {1}.

Bài 9 trang 27 Toán lớp 10 Tập 1: Cho A = {x ∈ ℝ|1 – 2x ≤ 0}, B = {x ∈ ℝ |x – 2 < 0}. Tìm A∩B, A∪B.

Lời giải:

Ta có: A = {x $\in$ℝ | 1 – 2x ≤ 0} = {x $\in$ℝ | x ≥ $\frac{1}{2}$} = $\left[\frac{1}{2};+\infty \right)$.

Ta lại có B = {x $\in$ℝ | x – 2 < 0} = {x $\in$ℝ | x < 2} = (- ∞; 2).

Ta có sơ đồ sau:

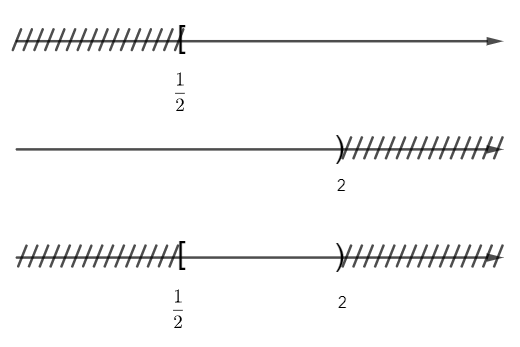
Suy ra A$\cap$B = $\text{[}\frac{1}{2};2)$

Suy ra A$\cup$B = (- ∞; + ∞)

Vậy A$\cap$B = $\text{[}\frac{1}{2};2)$ và A$\cup$B = (- ∞; + ∞).

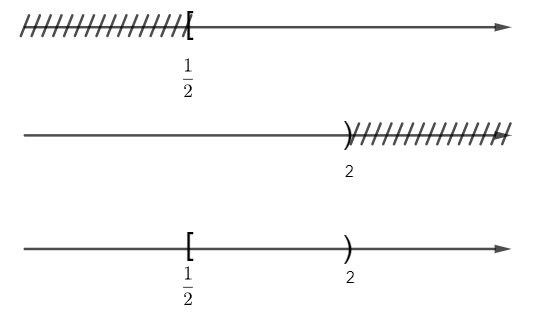
Bài 10 trang 27 Toán lớp 10 Tập 1: Lớp 10C có 45 học sinh, trong đó có 18 học sinh tham gia cuộc thi thiết kế đồ họa trên máy tính, 24 học sinh tham gia cuộc thi tin học văn phòng cấp trường và 9 học sinh không tham gia hai cuộc thi này. Hỏi có bao nhiêu học sinh của lớp 10C tham gia đồng thời hai cuộc thi.

Lời giải:

Ta có sơ đồ ven như sau:

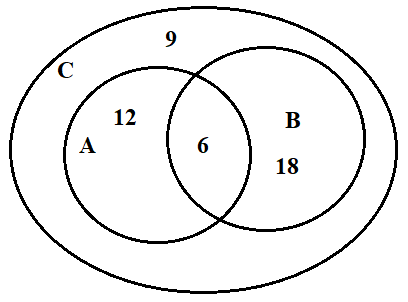
Ta có số học sinh tham gia ít nhất một trong hai cuộc thi là: 45 – 9 = 36 (học sinh).

Gọi A là tập hợp số học sinh tham gia cuộc thi vẽ đồ họa trên máy tính.

Gọi B là tập hợp số học sinh tham gia cuộc thi tin học văn phòng.

Khi đó n(A) = 18, n(B) = 24 và n(A∪B) = 36.

Số học sinh tham gia đồng thời cả hai cuộc thi là: n(A) + n(B) – n(A∪B) = 18 + 24 -36 = 6.

Vậy có 6 học sinh của lớp 10C tham gia đồng thời cả hai cuộc thi.

Lý thuyết Toán 10 Bài tập cuối chương 1 - Chân trời sáng tạo

1. Mệnh đề

- Những khẳng định có tính hoặc đúng hoặc sai được gọi là mệnh đề logic (hay mệnh đề).

- Mệnh đề là một khẳng định đúng hoặc sai.

- Một khẳng định đúng gọi là mệnh đề đúng.

- Một khẳng định sai gọi là mệnh đề sai.

- Một mệnh đề không thể vừa đúng vừa sai.

Chú ý:

+ Người ta thường sử dùng các chữ cái in hoa P, Q, R, … để kí hiệu các mệnh đề.

+ Những mệnh đề liên quan đến toán học được gọi là mệnh đề toán học.

2. Mệnh đề chứa biến

- Mệnh đề chứa biến là mệnh đề chưa khẳng định được tính đúng sai, cần có giá trị cụ thể của biến mới có thể khẳng định tính đúng sai của mệnh đề đó.

- Ta thường kí hiệu mệnh đề chứa biến n là P (n).

- Một mệnh đề chứa biến có thể chứa một biến hoặc nhiều biến.

3. Mệnh đề phủ định

- Mỗi mệnh đề P có mệnh đề phủ định, kí hiệu là .

- Mệnh đề P và mệnh đề phủ định của nó có tính đúng sai trái ngược nhau. Nghĩa là khi P đúng thì sai, khi P sai thì đúng.

Nhận xét:

+ Thông thường để phủ định một mệnh đề, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề đó.

4. Mệnh đề kéo theo

- Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, kí hiệu là P ⇒ Q.

- Mệnh đề P ⇒ Q chỉ sai khi P đúng và Q sai.

Nhận xét:

+ Mệnh đề P ⇒ Q còn được phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.

+ Để xét tính đúng sai của mệnh đề P ⇒ Q, ta chỉ cần xét trường hợp P đúng. Khi đó, nếu Q đúng thì mệnh đề đúng, nếu Q sai thì mệnh đề sai. Ta đã quen với điều này khi chứng minh nhiều định lí ở Trung học cơ sở.

5. Mệnh đề đảo. Hai mệnh đề tương đương

- Mệnh đề Q ⇒ P được gọi là mệnh đề đảo của mệnh đề P ⇒ Q.

Chú ý: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.

- Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng thì ta nói P và Q là hai mệnh đề tương đương, kí hiệu là P ⇔ Q (đọc là “P tương đương Q” hoặc “P khi và chỉ khi Q”).

- Khi đó ta cũng nói P là điều kiện cần và đủ để có Q (hay Q là điều kiện cần và đủ để có P).

Nhận xét: Hai mệnh đề P và Q tương đương khi chúng cùng đúng hoặc cùng sai.

6. Mệnh đề chứa kí hiệu ∀ và ∃

- Kí hiệu ∀ đọc là “với mọi”.

- Kí hiệu ∃ đọc là “tồn tại”.

- Mệnh đề “∀x ∈ M, P(x)” đúng nếu với mọi x₀ ∈ M, P(x₀) là mệnh đề đúng.

- Mệnh đề “∃x ∈ M, P(x)” đúng nếu có x₀ ∈ M sao cho P(x₀) là mệnh đề đúng.

7. Nhắc lại về tập hợp

- Trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.

- Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa A, B, C, … và kí hiệu phần tử của tập hợp bằng các chữ cái in thường a, b, c, ….

Chú ý: Đôi khi, để ngắn gọn, người ta dùng từ “tập” thay cho “tập hợp”.

- Để chỉ a là một phần tử của tập hợp A, ta viết a ∈ A (đọc là “a thuộc A”). Để chỉ a không là phần tử của tập hợp A, ta viết a ∉ A (đọc là “a không thuộc A”).

- Một tập hợp có thể không chứa phần tử nào. Tập hợp như vậy gọi là tập rỗng, kí hiệu ∅.

- Người ta thường kí hiệu các tập hợp số như sau: ℕ là tập hợp các số tự nhiên, ℤ là tập hợp các số nguyên, ℚ là tập hợp các số hữu tỉ, ℝ là tập hợp các số thực.

*Cách xác định tập hợp

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

Chú ý: Khi liệt kê các phần tử của tập hợp, ta có một số chú ý sau đây:

+ Các phần tử có thể được viết theo thứ tự tùy ý.

+ Mỗi phần tử chỉ được liệt kê một lần.

+ Nếu quy tắc xác định các phần tử đủ rõ thì người ta dùng “…” mà không nhất thiết viết ra tất cả các phần tử của tập hợp.

- Có những tập hợp ta có thể đếm hết các phần tử của chúng. Những tập hợp như vậy được gọi là tập hợp hữu hạn.

8. Tập con và hai tập hợp bằng nhau

- Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A ⊂ B (đọc là A chứa trong B), hoặc B ⊃ A (đọc là B chứa A).

Nhận xét:

+ A ⊂ A và ∅ ⊂ A với mọi tập hợp A.

+ Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B (đọc là A không chứa trong B hoặc B không chứa A).

+ Nếu A ⊂ B hoặc B ⊂ A thì ta nói A và B có quan hệ bao hàm.

- Trong toán học, người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường cong kín, gọi là biểu đồ Ven.

Chú ý: Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu tỉ, tập số thực), ta có quan hệ bao hàm: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.

9. Một số tập con của tập hợp số thực

- Ta thường sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a < b):

- Trong các kí hiệu trên, kí hiệu - ∞ đọc là âm vô cực

10. Hợp và giao của các tập hợp

- Cho hai tập hợp A và B.

Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A ∪ B.

A ∪ B = {x| x ∈ A hoặc x ∈ B}.

Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A ∩ B.

A ∩ B = {x | x ∈ A và x ∈ B}.

Nhận xét:

+ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

+ Đặc biệt, nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).

11. Hiệu của hai tập hợp, phần bù của tập con

- Cho hai tập hợp A và B.

Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\B.

A\B = {x | x ∈ A và x ∉ B}.

Nếu A là tập con của E thì hiệu E\A gọi là phần bù của A trong E, kí hiệu C_EA.

Chú ý: Trong các chương sau, để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 1

Trắc nghiệm Ôn tập chương 1