Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 10

Giải bài tập Toán 10 Bài tập cuối chương 10

Giải Toán 10 trang 86 Tập 2

Bài tập 1 trang 86 Toán lớp 10 Tập 2: Chọn ngẫu nhiên một số nguyên dương có ba chữ số:

a) Hãy mô tả không gian mẫu.

b) Tính xác suất biến cố “Số được chọn là lập phương của một số nguyên”.

c) Tính xác suất của biến cố “Số được chọn chia hết cho 5”.

Lời giải:

a) Chọn ngẫu nhiên một số nguyên dương có ba chữ số tức là chọn ngẫu nhiên một số trong các số 100; 101; 102; 103; ...; 997; 998; 999.

Khi đó, các kết quả có thể của phép thử là: {100; 101; 102; 103; ...; 997; 998; 999}.

Do đó, ta có không gian mẫu của phép thử là: Ω = {100; 101; 102; 103; ...; 997; 998; 999}.

Vậy Ω = {100; 101; 102; 103; ...; 997; 998; 999}.

b) Ta có, số phần tử của không gian mẫu là: n(Ω) = 999 – 100 + 1 = 900.

Gọi B là biến cố “Số được chọn là lập phương của một số nguyên”.

Ta có: 1³ = 1; 2³ = 8; 3³ = 27; 4³ = 64; 5³ = 125;

6³ = 216; 7³ = 343; 8³ = 512; 9³ = 729; 10³ = 10000.

Suy ra, các kết quả thuận lợi cho biến cố B là: 125; 216; 343; 512; 729.

⇒ B = {125; 216; 343; 512; 729}

⇒ n(B) = 5

⇒ Xác suất của B là: P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}$ = $\frac{5}{900}$ = $\frac{1}{180}$ .

Vậy xác suất biến cố “Số được chọn là lập phương của một số nguyên” là $\frac{1}{180}$ .

c) Gọi C là biến cố “Số được chọn là số chia hết cho 5”.

⇒ Các kết quả thuận lợi cho C là: 100; 105; 110; 115; ...; 990; 995.

⇒ C = {100; 105; 110; 115; ...; 990; 995}

⇒ n(C) = $\frac{995-100}{5}+1$ = 180.

⇒ Xác suất của C là: P(C) = $\frac{n\left(C\right)}{n\left(\Omega \right)}$ = $\frac{180}{900}$ = $\frac{1}{5}$ .

Vậy xác suất của biến cố “Số được chọn chia hết cho 5” là $\frac{1}{5}$ .

Bài tập 2 trang 86 Toán lớp 10 Tập 2: Gieo bốn đồng xu cân đối và đồng chất. Xác định biến cố đối của mỗi biến cố sau và tính xác suất của nó.

a) “Xuất hiện ít nhất ba mặt sấp”;

b) “Xuất hiện ít nhất một mặt ngửa”.

Lời giải:

a) Khi gieo một đồng xu cân đối, đồng chất thì có hai kết quả có thể là đồng xu xuất hiện mặt sấp (S) hoặc đồng xu xuất hiện mặt ngửa (N).

Khi đó, gieo bốn đồng xu cân đối và đồng chất thì có 2.2.2.2 = 2⁴ = 16 kết quả có thể.

⇒ n(Ω) = 2⁴ = 16.

Gọi A là biến cố “Xuất hiện ít nhất ba mặt sấp”.

Khi đó A không xảy ra khi xuất hiện nhiều nhất hai mặt sấp, tức là xuất hiện ít nhất hai mặt ngửa.

Do đó biến cố đối của biến cố A là $\overline{A}$ : “Xuất hiện ít nhất hai mặt ngửa”.

Ta có các kết quả thuận lợi cho biến cố A là: NSSS; SNSS; SSNS; SSSN; SSSS

⇒ A = {NSSS; SNSS; SSNS; SSSN; SSSS}

⇒ n(A) = 5

⇒ P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{5}{16}$ .

Vậy xác suất của biến cố “Xuất hiện ít nhất ba mặt sấp” là $\frac{5}{16}$ .

b) Gọi B là biến cố “Xuất hiện ít nhất một mặt ngửa”.

Khi đó B không xảy ra khi không xuất hiện mặt ngửa nào.

⇒ Biến cố đối của biến cố B là $\overline{B}$ “Không xuất hiện mặt ngửa nào”.

⇒ $\overline{B}$ = {SSSS} ⇒ n( $\overline{B}$) = 1.

⇒ P( $\overline{B}$) = $\frac{1}{16}$ .

⇒ P(B) = 1 – P( $\overline{B}$) = 1 – $\frac{1}{16}$ = $\frac{15}{16}$ .

Vậy tính xác suất của biến cố “Xuất hiện ít nhất một mặt ngửa” là $\frac{15}{16}$ .

Bài tập 3 trang 86 Toán lớp 10 Tập 2: Gieo ba con xúc xắc cân đối và đồng chất. Tính xác suất của mỗi biến cố sau:

a) “Tổng số chấm xuất hiện nhỏ hơn 5”;

b) “Tích số chấm xuất hiện chia hết cho 5”.

Lời giải:

Gieo một con xúc xắc thì có 6 kết quả có thể.

Khi gieo ba con xúc xắc thì sẽ có 6.6.6 = 6³ = 216 kết quả có thể.

⇒ n(Ω) = 6³ = 216.

a) Gọi A là biến cố “Tổng số chấm xuất hiện nhỏ hơn 5”.

Vì số chấm nhỏ nhất trên mỗi xúc xắc là 1, nên tổng số chấm xuất hiện sau khi thực hiện phép thử luôn lớn hơn hoặc bằng 3.

Ta có: 3 = 1 + 1 + 1

4 = 1 + 1 + 2 = 1 + 2 + 1 = 2 + 1 + 1

⇒ A = {(1; 1; 1), (1; 1; 2), (1; 2; 1), (2; 1; 1)}

⇒ n(A) = 4

⇒ Xác suất của biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{4}{216}$ = $\frac{1}{54}$ .

Vậy xác suất của biến cố “Tổng số chấm xuất hiện nhỏ hơn 5” là $\frac{1}{54}$ .

b) Gọi B là biến cố “Tích số chấm xuất hiện chia hết cho 5”.

⇒ Biến cố đối của biến cố B là $\overline{B}$ : “Tích số chấm xuất hiện không chia hết cho 5”.

Để tích số chấm không chia hết cho 5 thì kết quả của phép thử không được xuất hiện mặt 5 chấm.

Tức là mỗi con xúc xắc xuất hiện một trong các mặt {1; 2; 3; 4; 6}.

Khi đó, số kết quả thuận lợi cho $\overline{B}$ là : 5. 5. 5 =5³ = 125.

⇒ n( $\overline{B}$) = 5³ = 125.

⇒ P( $\overline{B}$) = $\frac{125}{216}$.

⇒ Xác suất của biến cố B là P(B) = 1 – P( $\overline{B}$) = 1 – $\frac{125}{216}$ = $\frac{91}{216}$ .

Vậy xác suất “Tích số chấm xuất hiện chia hết cho 5” là $\frac{91}{216}$ .

Bài tập 4 trang 86 Toán lớp 10 Tập 2: Hộp thứ nhất chứa 4 viên bi xanh, 3 viên bi đỏ. Hộp thứ hai chứa 5 viên bi xanh, 2 viên bi đỏ. Các viên có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên từ mỗi hộp 2 viên bi. Tính xác suất của mỗi biến cố sau:

a) “Bốn viên bi lấy ra có cùng màu”;

b) “Trong 4 viên bi lấy ra có đúng 1 viên bi xanh”;

c) “Trong 4 viên bi lấy ra có đủ cả bi xanh và bi đỏ”.

Lời giải:

Hộp thứ nhất chứa 4 viên bi xanh, 3 viên bi đỏ nên có tổng số viên bi là: 4 + 3 = 7.

Hộp thứ hai chứa 5 viên bi xanh, 2 viên bi đỏ nên có tổng số viên bi là: 5 + 2 = 7.

Lấy ra ngẫu nhiên từ hộp thứ nhất 2 viên bi, ta có: $C_7^2$ cách chọn.

Lấy ra ngẫu nhiên từ hộp thứ hai 2 viên bi, ta có: $C_7^2$ cách chọn.

Theo quy tắc nhân, số cách để lấy ra ngẫu nhiên từ mỗi hộp 2 viên bi là $C_7^2$ .$C_7^2$ = 441.

⇒ Số kết quả có thể xảy ra của phép thử trên là: n(Ω) = $C_7^2$ . $C_7^2$ = 441.

a) Gọi A là biến cố “Bốn viên bi lấy ra có cùng màu”.

Khi đó hoặc là 4 viên bi lấy ra đều là màu xanh, hoặc 4 viên bi lấy ra đều là màu đỏ.

- Nếu 4 viên bi lấy ra đều là màu xanh thì:

+ Lấy được 2 bi xanh trong 4 bi xanh của hộp thứ nhất, có $C_4^2$ cách;

+ Lấy được 2 bi xanh trong 5 bi xanh của hộp thứ 2, có $C_5^2$ cách.

Theo quy tắc nhân ta có số cách để lấy ra 2 bi xanh trong hộp thứ nhất và 2 bi xanh trong hộp thứ hai là: $C_4^2$ . $C_5^2$ cách.

- Nếu 4 viên bi lấy ra đều là màu đỏ thì:

+ Lấy được 2 bi đỏ trong 3 bi đỏ của hộp thứ nhất, có $C_3^2$ cách;

+ Lấy được 2 bi đỏ trong 2 bi đỏ của hộp thứ 2, có $C_2^2$ cách.

Theo quy tắc nhân ta có số cách để lấy ra 2 bi đỏ trong hộp thứ nhất và 2 bi đỏ trong hộp thứ hai là: $C_3^2$ $C_2^2$ cách.

Khi đó, theo quy tắc cộng, số cách để lấy ra 4 viên bi cùng màu là:

⇒ Số các kết quả thuận lợi cho A là 63.

⇒ n(A) = 63.

Xác suất của biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{63}{441}$ = $\frac{1}{7}$ .

Vậy xác suất của biến cố “Bốn viên bi lấy ra có cùng màu” là: $\frac{1}{7}$ .

b) Gọi B là biến cố “Trong 4 viên bi lấy ra có đúng 1 viên bi xanh”.

Ta có các trường hợp sau :

* Trường hợp 1 : 1 viên bi xanh được lấy ra từ hộp 1, còn 3 viên bi còn lại đều màu đỏ.

- Trong hộp thứ nhất:

+ Lấy được 1 viên bi xanh trong 4 bi xanh có $C_4^1$ cách.

+ Lấy được 1 viên bi đỏ trong 3 viên bi đỏ ta có: $C_3^1$ cách.

- Hộp thứ hai 2 viên bi lấy ra đều là bi đỏ, ta có $C_2^2$ cách.

Theo quy tắc nhân ta có $C_4^1$ . $C_3^1$. $C_2^2$ cách lấy ra 4 viên bi, trong đó có 1 viên bi xanh trong hộp thứ nhất còn lại là 3 viên bi đỏ.

* Trường hợp 2 : 1 viên bi xanh được lấy ra từ hộp 2, còn 3 viên bi còn lại đều màu đỏ.

- Trong hộp thứ nhất: 2 viên bi lấy ra đều là bi đỏ, ta có $C_3^2$ cách.

- Trong hộp thứ hai:

+ Lấy được 1 viên bi xanh trong 5 bi xanh có $C_5^1$ cách.

+ Lấy được 1 viên bi đỏ trong 2 viên bi đỏ ta có: cách.

Theo quy tắc nhân ta có $C_3^2$ . $C_5^1$. $C_2^1$ cách lấy ra 4 viên bi, trong đó có 1 viên bi xanh trong hộp thứ hai còn lại là 3 viên bi đỏ.

Khi đó, theo quy tắc cộng ta có 42 cách để lấy ra 4 viên bi có đúng 1 viên bi màu xanh.

⇒ Số các kết quả thuận lợi cho B là: n(B) = 42

Xác suất của biến cố B là: P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}$ = $\frac{42}{441}$ = $\frac{2}{21}$ .

Vậy xác suất của biến cố “Trong 4 viên bi lấy ra có đúng 1 viên bi xanh” là: $\frac{2}{21}$ .

c) Gọi C là biến cố “Trong bốn viên lấy ra có đủ cả bi xanh và bi đỏ”.

⇒ Biến cố đối của biến cố C là $\overline{C}$ : “Bốn viên bi lấy ra có cùng màu”.

Theo phần a, ta tính được P( $\overline{C}$) = $\frac{1}{7}$ .

⇒ Xác suất của biến cố C là: P(C) = 1 – P( $\overline{C}$) = 1 – $\frac{1}{7}$ = $\frac{6}{7}$ .

Vậy xác suất của biến cố “Trong bốn viên lấy ra có đủ cả bi xanh và bi đỏ” là $\frac{6}{7}$ .

Bài tập 5 trang 86 Toán lớp 10 Tập 2: Một nhóm học sinh được chia vào 4 tổ, mỗi tổ có 3 học sinh. Chọn ra ngẫu nhiên từ nhóm đó 4 học sinh. Tính xác suất của mỗi biến cố sau:

a) “Bốn bạn thuộc 4 tổ khác nhau”;

b) “Bốn bạn thuộc 2 tổ khác nhau”.

Lời giải:

Có 4 tổ và mỗi tổ có 3 học sinh nên ta có tổng số học sinh là: 4.3 = 12 học sinh.

Chọn ngẫu nhiên 4 học sinh trong 12 học sinh nên ta có $C_{12}^4$ cách chọn.

⇒ Số phần tử của không gian mẫu là: n(Ω) = $C_{12}^4$ = 495

a) Gọi A là biến cố “Bốn bạn thuộc 4 tổ khác nhau”.

Khi đó, mỗi tổ ta chọn 1 học sinh trong 3 học sinh được chia vào tổ đó, ta có $C_3^1$ cách chọn.

Do có 4 tổ nên theo quy tắc nhân ta có $C_3^1{C}_3^1{C}_3^1{C}_3^1$ cách chọn bốn bạn thuộc 4 tổ khác nhau.

⇒ n(A) = $C_3^1{C}_3^1{C}_3^1{C}_3^1$ = 81.

Xác suất của biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{81}{495}$ = $\frac{9}{55}$ .

Vậy xác suất của mỗi biến cố “Bốn bạn thuộc 4 tổ khác nhau” là $\frac{9}{55}$ .

b) Gọi B là biến cố “Bốn bạn thuộc hai tổ khác nhau”.

Ta có, chọn 2 tổ trong 4 tổ có $C_4^2$ cách chọn.

+ Trường hợp 1: Chọn mỗi tổ 2 người, có $C_3^2{C}_3^2$ cách.

+ Trường hợp 2: Chọn một tổ 3 người, một tổ 1 người, ta có 2. $C_3^1$ . $C_3^3$ cách.

Theo quy tắc nhân và cộng ta có: 90 cách chọn ra 2 tổ sau đó chọn ra 4 bạn trong 2 tổ đó.

⇒ Số kết quả thuận lợi cho biến cố B là: n(B) = 90.

Xác suất của biến cố B là: P(B) = $\frac{90}{495}$ = $\frac{2}{11}$ .

Vậy xác suất của biến cố “Bốn bạn thuộc hai tổ khác nhau” là $\frac{2}{11}$ .

Bài tập 6 trang 86 Toán lớp 10 Tập 2: Một cơ thể có kiểu gen là AaBbDdEe, các cặp alen nằm trên các cặp nhiễm sắc thể tương đồng khác nhau. Chọn ngẫu nhiên một giao tử của cơ thể sau khi giảm phân. Giả sử tất cả các giao tử sinh ra có sức sống như nhau. Tính xác suất để giao tử được chọn mang đầy đủ các alen trội.

Lời giải:

Cơ thể có kiểu gen AaBbDdEe giảm phân bình thường cho ta 2⁴ = 16 giao tử như sau:

ABDE; ABDe; ABde; Abde; AbDE; ABdE; AbDe; AbdE; aBDE; aBDe; aBde; abde; abDE; aBdE; abDe; abdE.

Khi đó, ta có không gian mẫu là :

Ω = {ABDE; ABDe; ABde; Abde; AbDE; ABdE; AbDe; AbdE; aBDE; aBDe; aBde; abde; abDE; aBdE; abDe; abdE}.

⇒ n(Ω) = 16.

Gọi A là biến cố “Giao tử được chọn mang đầy đủ các alen trội”.

Khi đó kết quả thuận lợi cho A là ABDE, tức là A = {ABDE}.

⇒ n(A) = 1.

⇒ P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{1}{16}$ .

Vậy xác suất để giao tử được chọn mang đầy đủ các alen trội là $\frac{1}{16}$ .

Bài tập 7 trang 86 Toán lớp 10 Tập 2: Sắp xếp 5 tấm thẻ cùng loại được đánh số từ 1 đến 5 một cách ngẫu nhiên để tạo thành một số tự nhiên a có 5 chữ số. Tính xác suất của mỗi biến cố sau:

a) “a là số chẵn”;

b) “a chia hết cho 5”;

c) “a ≥ 32 000”;

d) “Trong các chữ số của a không có 2 chữ số lẻ nào đứng cạnh nhau”.

Lời giải:

Sắp xếp 5 tấm thẻ cùng loại được đánh số từ 1 đến 5 một cách ngẫu nhiên để tạo thành một số tự nhiên a có 5 chữ số ta có 5! = 120 cách xếp.

⇒ Số phần tử của không gian mẫu là: n(Ω) = 5! = 120.

a) Gọi A là biến cố “a là số chẵn”.

Vì a là số chẵn nên có hai cách chọn ra chữ số hàng đơn vị là 2 hoặc 4, ta có $C_2^1$ cách chọn; xếp 4 chỗ còn lại có 4! cách.

Theo quy tắc nhân ta có 2.4! cách chọn để a là số chẵn.

⇒ Số phần tử thuận lợi cho biến cố A: “a là số chẵn” là: n (A) = 2.4! = 48

⇒ Xác suất của biến cố A : “a là số chẵn” là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{48}{120}$ = $\frac{2}{5}$.

Vậy xác suất của biến cố “a là số chẵn” là $\frac{2}{5}$ .

b) Gọi B là biến cố “a chia hết cho 5”.

Do a chia hết cho 5 nên chữ số hàng đơn vị nhận giá trị 5 nên chỉ có 1 cách xếp hàng đơn vị. 4 chỗ còn lại có 4! cách.

Theo quy tắc nhân ta có 1.4! cách chọn để a chia hết cho 5.

⇒ Số phần tử thuận lợi cho biến cố B: “a là số chia hết cho 5” là: n(B) = 1.4! = 24.

⇒ Xác suất của biến cố B: “a là số chia hết cho 5” là: P(B) = $\frac{24}{120}$ = $\frac{1}{5}$ .

Vậy xác suất của biến cố “a là số chia hết cho 5” là $\frac{1}{5}$ .

c) Gọi C là biến cố “a ≥ 32 000”.

Để a ≥ 32 000 ta có các trường hợp sau :

Trường hợp 1: Chọn chữ số hàng chục nghìn là 4 hoặc 5 có 2 cách chọn, còn 4 vị trí còn lại có 4! cách chọn,

Theo quy tắc nhân, ta có 2. 4! = 48 (cách chọn).

Trường hợp 2: Chọn chữ số hàng chục nghìn là 3 có 1 cách chọn, thì chữ số hàng nghìn có 3 cách chọn {2, 4, 5}, 3 số còn lại có 3! cách xếp .

Theo quy tắc nhân, Có 1.3.3! = 18 cách xếp.

Khi đó, theo quy tắc cộng ta có: 48 + 18 = 66 cách xếp để a ≥ 32 000.

⇒ Số phần tử thuận lợi cho biến cố C: “a ≥ 32 000” là: n(C) = 66.

⇒ Xác suất của biến cố C: “a ≥ 32 000” là: P(C) = $\frac{66}{120}$ = $\frac{11}{20}$ .

Vậy xác suất của biến cố “a ≥ 32 000” là $\frac{11}{20}$ .

d) Gọi D là biến cố: “Trong các chữ số của a không có 2 chữ số lẻ nào đứng cạnh nhau”.

Số a không có hai chữ số lẻ nào đứng cạnh nhau có dạng: x2x4x hoặc x4x2x

Khi đó ta thấy chữ số 2 và 4 có 2 cách xếp, còn 3 vị trí còn lại có 3! cách xếp.

Theo quy tắc nhân, ta có 2.3! cách xếp để trong các chữ số của a không có 2 chữ số lẻ nào đứng cạnh nhau”.

⇒ Số phần tử thuận lợi cho biến cố D: “Trong các chữ số của a không có 2 chữ số lẻ nào đứng cạnh nhau” là: n(D)= 2.3! = 12.

⇒ Xác suất của biến cố trên là: P(D) = $\frac{12}{120}$ = $\frac{1}{10}$ .

Vậy xác suất của biến cố “Trong các chữ số của a không có 2 chữ số lẻ nào đứng cạnh nhau” là $\frac{1}{10}$ .

Bài tập 8 trang 86 Toán lớp 10 Tập 2: Lớp 10A có 20 bạn nữ, 25 bạn nam. Lớp 10B có 24 bạn nữ, 21 bạn nam. Chọn ngẫu nhiên từ mỗi lớp ra hai bạn đi tập văn nghệ. Tính xác suất của mỗi biến cố sau:

a) “Trong 4 bạn được chọn có ít nhất 1 bạn nam”;

b) “Trong 4 bạn được chọn có đủ cả nam và nữ”.

Lời giải:

Lớp 10A có 20 bạn nữ, 25 bạn nam nên có tổng số học sinh là 20 + 25 = 45 bạn.

Lớp 10B có 24 bạn nữ, 21 bạn nam nên có tổng số học sinh là 24 + 21 = 45 bạn.

Chọn ngẫu nhiên từ mỗi lớp ra hai bạn đi tập văn nghệ nên ta chọn:

+ 2 bạn trong 45 bạn của lớp 10A, ta có $C_{45}^2$ cách chọn.

+ 2 bạn trong 45 bạn của lớp 10B, ta có $C_{45}^2$ cách chọn.

Theo quy tắc nhân, ta có . cách chọn từ mỗi lớp ra hai bạn đi tập văn nghệ.

⇒ Số kết quả có thể xảy ra của phép thử là: n(Ω) = $C_{45}^2{C}_{45}^2$ = 980 100.

a) Gọi A là biến cố “Trong bốn bạn được chọn có ít nhất 1 bạn nam”

⇒ Biến cố đối của biến cố A là $\overline{A}$ : “Không bạn nam nào được chọn”.

Khi đó ta chọn mỗi lớp 2 bạn nữ.

- Lớp 10A chọn 2 trong 20 bạn nữ, có $C_{20}^2$ cách chọn.

- Lớp 10B chọn 2 trong 24 bạn nữ, có $C_{24}^2$ cách chọn.

Theo quy tắc nhân, ta có $C_{20}^2$ . $C_{24}^2$ cách mà không có bạn nam nào được chọn.

⇒ Số kết quả thuận lợi cho biến cố $\overline{A}$ là: n( $\overline{A}$) = 52 440.

⇒ P( $\overline{A}$) = $\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}$ = $\frac{52440}{980100}$ .

Xác suất của biến cố A là: P(A) = 1 – P( $\overline{A}$) = 1 – $\frac{52440}{980100}$ = $\frac{927660}{980100}$ ≈ 0,946.

Vậy xác suất của biến cố “Trong 4 bạn được chọn có ít nhất 1 bạn nam” khoảng 0,946.

b) Gọi B là biến cố “Trong 4 bạn được chọn có đủ cả nam và nữ”

⇒ Biến cố đối của biến cố B là $\overline{B}$ : “4 bạn chọn ra đều là nam hoặc đều là nữ”

- Trường hợp 1: 4 bạn được chọn ra đều là nam.

+ Lớp 10A chọn 2 bạn nam trong 25 bạn nam, ta có: $C_{25}^2$ cách chọn.

+ Lớp 10B chọn 2 bạn nam trong 21 bạn nam, ta có: $C_{21}^2$ cách chọn.

Theo quy tắc nhân ta có : $C_{25}^2$ . $C_{21}^2$ cách chọn 4 bạn đều là nam.

- Trường hợp 2 : 4 bạn được chọn ra đều là nữ.

- Lớp 10A chọn 2 trong 20 bạn nữ, có $C_{20}^2$ cách chọn.

- Lớp 10B chọn 2 trong 24 bạn nữ, có $C_{24}^2$ cách chọn.

Theo quy tắc nhân, ta có $C_{20}^2$ . $C_{24}^2$ cách chọn 4 bạn đều là nữ.

Theo quy tắc cộng ta có $C_{25}^2$ . $C_{21}^2$ + có $C_{20}^2$ . $C_{24}^2$ cách chọn 4 bạn chọn ra đều là nam hoặc đều là nữ.

⇒ Số kết quả thuận lợi cho biến cố $\overline{B}$ là: n( $\overline{B}$) = 115 440.

⇒ P( $\overline{B}$) =$\frac{115440}{980100}$.

⇒ Xác suất của biến cố B là: P(B) = 1 – $\frac{115440}{980100}$ = $\frac{864660}{980100}$ ≈ 0,882.

Vậy xác suất của biến cố “Trong 4 bạn được chọn có đủ cả nam và nữ” khoảng 0,882.

Bài tập 9 trang 86 Toán lớp 10 Tập 2: Trong hộp có 5 bóng xanh, 6 bóng đỏ và 2 bóng vàng. Các bóng có kích thước và khối lượng như nhau. Lấy 2 bóng từ hộp, xem màu, trả lại hộp rồi lại lấy tiếp 1 bóng nữa từ hộp. Tính xác suất của mỗi biến cố sau:

a) “Ba bóng lấy ra cùng màu”;

b) “Bóng lấy ra lần 2 là bóng xanh”;

c) “Ba bóng lấy ra có 3 màu khác nhau”.

Lời giải:

Trong hộp có 5 bóng xanh, 6 bóng đỏ và 2 bóng vàng nên tổng số bóng là: 5 + 6 + 2 = 13 quả bóng.

- Lấy 2 bóng từ hộp có $C_{13}^2$ cách;

- Sau đó xem màu, trả lại hộp rồi lại lấy tiếp 1 bóng nữa từ hộp có $C_{13}^1$ cách.

Theo quy tắc nhân, ta có $C_{13}^2$ . $C_{13}^1$ = 1 014 cách lấy 2 bóng từ hộp, xem màu, trả lại hộp rồi lại lấy tiếp 1 bóng nữa từ hộp.

⇒ Số kết quả có thể xảy ra của phép thử là: n(Ω) = 1 014.

a) Gọi A là biến cố “Ba bóng lấy ra cùng màu”.

- Trường hợp 1: Lấy được 2 quả bóng màu xanh trong 5 quả bóng xanh, sau khi bỏ vào lại lấy được 1 quả bóng xanh trong 5 quả bóng xanh, ta có 50 cách.

- Trường hợp 2: Lấy được 2 quả bóng màu đỏ trong 6 quả bóng đỏ, sau khi bỏ vào lại lấy được 1 quả bóng đỏ trong 6 quả bóng đỏ, ta có 90 cách.

- Trường hợp 3: Lấy được 2 quả bóng màu vàng trong 2 quả bóng vàng, sau khi bỏ vào lại lấy được 1 quả bóng vàng trong 2 quả bóng vàng, ta có 2 cách.

Theo quy tắc cộng, ta có: 50 + 90 + 2 = 142 cách lấy sao cho ba bóng lấy ra cùng màu.

⇒ Số kết quả thuận lợi cho biến cố A là: n(A) = 142.

⇒ Xác suất của biến cố A là: P(A) = $\frac{142}{1014}$ = $\frac{71}{507}$ .

Vậy xác suất của biến cố “Ba bóng lấy ra cùng màu” là $\frac{71}{507}$ .

b) Gọi B là biến cố “Bóng lấy ra lần 2 là bóng xanh”.

Khi đó 2 quả bóng lấy ra lần 1 là tùy ý nên có $C_{13}^2$ cách lấy, lần 2 là bóng xanh nên ta có $C_5^1$ cách lấy.

Theo quy tắc nhân ta có $C_{13}^2$ . $C_5^1$ cách lấy sao cho bóng lấy ra lần 2 là bóng xanh.

⇒ Số kết quả thuận lợi cho biến cố B là: n(B) = $C_{13}^2$ . $C_5^1$ = 390.

Xác suất của biến cố B là: P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}$ = $\frac{5}{13}$ .

Vậy xác suất của biến cố “Bóng lấy ra lần 2 là bóng xanh” là $\frac{5}{13}$ .

c) Gọi C là biến cố “Ba bóng lấy ra có 3 màu khác nhau”.

Khi đó ta lấy được 1 bóng màu xanh, 1 bóng màu đỏ và 1 bóng màu vàng.

- Trường hợp 1:

+ 2 quả bóng lấy ra ở lần 1 là màu xanh và đỏ, ta có $C_5^1$ . $C_6^1$ cách lấy

+ Bóng lấy ra lần 2 là màu vàng, ta có $C_2^1$ cách lấy.

Khi đó, ta có $C_5^1$ . $C_6^1$. $C_2^1$ cách lấy 2 quả bóng lấy ra ở lần 1 là màu xanh và đỏ còn bóng lấy ra lần 2 là màu vàng.

- Trường hợp 2:

+ 2 quả bóng lấy ra ở lần 1 là màu xanh và vàng, ta có $C_5^1$ . $C_2^1$ cách lấy

+ Bóng lấy ra lần 2 là màu đỏ, ta có $C_6^1$ cách lấy.

Khi đó, ta có $C_5^1$ . $C_2^1$. $C_6^1$ cách lấy 2 quả bóng lấy ra ở lần 1 là màu xanh và vàng còn bóng lấy ra lần 2 là màu đỏ.

- Trường hợp 3:

+ 2 quả bóng lấy ra ở lần 1 là màu đỏ và vàng, ta có $C_6^1$ . $C_2^1$ cách lấy

+ Bóng lấy ra lần 2 là màu xanh, ta có $C_5^1$ cách lấy.

Khi đó, ta có $C_6^1$ . $C_2^1$. $C_5^1$ cách lấy 2 quả bóng lấy ra ở lần 1 là màu đỏ và vàng còn bóng lấy ra lần 2 là màu xanh.

Áp dụng quy tắc cộng ta có:

⇒ Số kết quả thuận lợi cho biến cố C là: n(C) = 180.

Xác suất của biến cố C là: P(C) = $\frac{n\left(C\right)}{n\left(\Omega \right)}$ = $\frac{30}{169}$ .

Vậy xác suất của biến cố “Ba bóng lấy ra có 3 màu khác nhau” là $\frac{30}{169}$ .

Lý thuyết Toán 10 Bài tập cuối chương 10 - Chân trời sáng tạo

1. Phép thử ngẫu nhiên và không gian mẫu

– Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó.

– Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu, kí hiệu là Ω.

– Chú ý: Trong chương này ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn phần tử.

Ví dụ: Xúc xắc có 6 mặt đánh số chấm từ 1 chấm đến 6 chấm. Không gian mẫu của 1 lần tung xúc xắc là Ω = {1; 2; 3; 4; 5; 6}.

Phép thử: Tung xúc xắc 2 lần sẽ có không gian mẫu gồm 6.6 = 36 cách xuất hiện mặt của xúc xắc.

2. Biến cố

– Mỗi tập con của không gian mẫu được gọi là một biến cố, kí hiệu là A, B, C, …

– Một kết quả thuộc A được gọi là kết quả làm cho A xảy ra, hoặc kết quả thuận lợi cho A.

– Biến cố chắc chắn là biến cố luôn xảy ra, kí hiệu là Ω.

– Biến cố không thể là biến cố không bao giờ xảy ra, kí hiệu là ∅.

– Đôi khi ta cần dùng các quy tắc đếm và công thức tổ hợp để xác định số phần tử của không gian mẫu và số kết quả thuận lợi cho mỗi biến cố.

Ví dụ: Một nhóm có 3 bạn nam và 2 bạn nữ. Chọn ngẫu nhiên cùng lúc 2 bạn đi làm vệ sinh lớp.

a) Xác định số phần tử của không gian mẫu.

b) Xác định số kết quả thuận lợi cho biến cố “Chọn được 1 bạn nam và 1 bạn nữ”.

Hướng dẫn giải

a) Do ta chọn 2 bạn khác nhau từ 5 bạn trong nhóm và không tính thứ tự nên số phần tử của không gian mẫu là $C_5^2$ = 10.

b) Chọn 1 bạn nữ từ 2 bạn nữ có $C_2^1$ = 2 cách chọn;

Chọn 1 bạn nam từ 3 bạn nam có $C_3^1$ = 3 cách chọn.

Theo quy tắc nhân có tất cả 2.3 = 6 cách chọn ra 1 bạn nam và 1 bạn nữ từ nhóm bạn.

Do đó số kết quả thuận lợi cho biến cố “Chọn được 1 bạn nam và 1 bạn nữ” là 6.

3. Xác suất của biến cố

– Giả sử một phép thử có không gian mẫu Ω gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố.

Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$

Trong đó n(A) và n($\Omega$) lần lượt là kí hiệu số phần tử của tập A và $\Omega$ .

Chú ý:

+ Định nghĩa trên được gọi là định nghĩa cổ điển của xác suất.

+ Với mọi biến cố A, 0 ≤ P(A) ≤ 1.

+ P($\Omega$) = 1, P(∅) = 0.

+ Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng gần 1.

Ví dụ: Trong hộp có 3 viên bi xanh và 5 viên bi đỏ. Lấy ngẫu nhiên trong hộp 3 viên bi. Tính xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ”.

Hướng dẫn giải

– Tính số phần tử của không gian mẫu:

Lấy 3 viên bi ngẫu nhiên trong 8 viên bi có $C_8^3$ cách.

Do đó số phần tử của không gian mẫu là n($\Omega$) = $C_8^3$ = 56.

– Tính số kết quả thuận lợi cho biến cố A:

Lấy được 3 viên bi màu đỏ trong số 5 viên bi màu đỏ có $C_5^3$ cách.

Do đó, số kết quả thuận lợi cho biến cố A là n(A) = $C_5^3$ = 10.

Xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ” là:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ =$\frac{10}{56}=\frac{5}{28}$

Vậy xác suất của biến cố A là P(A) = $\frac{5}{28}$ .

4. Tính xác suất bằng sơ đồ hình cây

– Trong chương VIII, chúng ta đã được làm quen với phương pháp sử dụng sơ đồ hình cây để liệt kê các kết quả của một thí nghiệm. Ta cũng có thể sử dụng sơ đồ hình cây để tính xác suất

Ví dụ: Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Tính xác suất của biến cố A: “Trong 3 lần tung có ít nhất 1 lần xuất hiện mặt ngửa”.

Hướng dẫn giải

Kí hiệu S nếu tung được mặt sấp, N nếu tung được mặt ngửa.

Các kết quả có thể xảy ra trong 3 lần tung được thể hiện trong sơ đồ hình cây dưới đây:

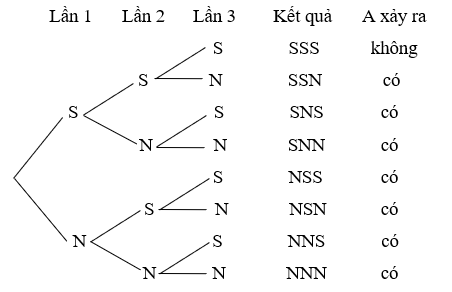
Có tất cả 8 kết quả xảy ra, trong đó có 7 kết quả thuận lợi cho biến cố A.

Do đó:

P(A) = $\frac{7}{8}$ .

5. Biến cố đối

– Cho A là một biến cố. Khi đó biến cố “Không xảy ra A”, kí hiệu là $\left(\overline{A}\right)$ , được gọi là biến cố đối của A.

$\overline{A}=\Omega \backslash A$; P$\left(\overline{A}\right)$ + P(A) = 1.

Ví dụ: Trong giỏ có 3 quả cam, 4 quả táo và 2 quả đào. Lấy ngẫu nhiên từ trong giỏ ra 4 quả. Tính xác suất để trong 4 quả lấy ra có ít nhất 1 quả táo.

Hướng dẫn giải

Gọi A là biến cố “Trong 4 quả lấy ra có ít nhất 1 quả táo”.

Thì biến cố đối của A là $\overline{A}$ : “Trong 4 quả lấy ra không có quả táo nào”.

Ta sẽ tính xác suất của biến cố $\overline{A}$ :

Lấy 4 quả trong tổng số 3 + 4 + 2 = 9 quả có cách.

Do đó, số phần tử của không gian mẫu là n$\left(\Omega \right)$= $C_9^4$ = 126.

Lấy 4 quả trong số 5 quả cam và đào thì có $C_5^4$cách.

Do đó, số kết quả thuận lợi cho biến cố $\overline{A}$ là: n($\overline{A}$) = $C_5^4$ = 5.

Xác suất của biến cố $\overline{A}$ là: P$\left(\overline{A}\right)$ =$\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{5}{126}$

Suy ra xác suất của biến cố A là:

P(A) = 1 – P$\left(\overline{A}\right)$ =$\frac{121}{126}$.

6. Nguyên lí xác suất bé

Trong thực tế, các biến cố có xác suất xảy ra gần bằng 1 thì gần như là luôn xảy ra trong một phép thử. Ngược lại, các biến cố mà xác suất xảy ra gần bằng 0 thi gần như không xảy ra trong một phép thử.

Trong Lí thuyết Xác suất, Nguyên lí xác suất bé được phát biểu như sau:

Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.

Ví dụ: Khi một con tàu lưu thông trên biển, xác suất nó bị đắm là số dương. Tuy nhiên, nếu tuân thủ các quy tắc an toàn thi xác suất xảy ra biển cố này là rất nhỏ, con tàu có thể yên tâm hoạt động.

Nếu một nhà sản xuất tuyên bố tỉ lệ gây sốc phản vệ nặng khi tiêm một loại vắc xin là rất nhỏ, chỉ khoảng 0,001, thì có thể tiêm vắc xin đó cho mọi người được không? Câu trả lời là không, vì sức khoẻ và tính mạng con người là vô giá, nếu tiêm loại vắc xin đó cho hàng tỉ người thì khả năng có nhiều người bị sốc phản vệ nặng là rất cao.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra

Bài 2: Vẽ ba đường conic bằng phần mềm Geogebra