Giải Toán 10 Bài 2 (Chân trời sáng tạo): Tập hợp

Giải bài tập Toán 10 Bài 2: Tập hợp

Video giải bài tập Toán 10 Bài 2: Tập hợp

Giải Toán 10 trang 16 Tập 1

Hoạt động khởi động trang 16 Toán lớp 10 Tập 1: Giả sử bạn có một giá sách và các quyển sách như hình dưới đây. Bạn sẽ xếp các quyển sách của mình lên giá như thế nào? Hãy giải thích.

Lời giải:

Chúng ta sẽ sắp xếp các cuốn sách thành các nhóm sau:

Ngăn thứ nhất của giá sách sẽ xếp các cuốn sách liên quan đến Toán học: Lịch sử toán học, Toán học vui.

Ngăn thứ hai của giá sách sẽ xếp các cuốn sách liên quan đến Văn học: Tuyển tập Nam Cao, Dế mèn phiêu lưu kí, Truyện ngắn chọn lọc, Hoàng Lê nhất thống trí.

Ngăn thứ ba của giá sách sẽ xếp các cuốn sách liên quan đến Lịch sử: Việt Nam sử lược, Lịch sử thế giới, Lịch sử Việt Nam.

Ngăn thứ tư của giá sách sẽ xếp các cuốn sách liên quan đến Khoa học: Khoa học vui, Vật lí thưởng thức.

Thực hành 1 trang 16 Toán lớp 10 Tập 1: a) Lấy ba ví dụ về tập hợp và chỉ ra một số phần tử của chúng.

b) Với mỗi tập hợp ℕ, ℤ, $\mathbb{Q}$, ℝ hãy sử dụng kí hiệu ∈ và ∉ để chỉ ra hai phần tử thuộc, hai phần tử không thuộc tập hợp đó.

Lời giải:

a) Cho tập A là tập các số tự nhiên nhỏ hơn 10, khi đó 1 $\in$ A, 3 $\in$ A, 5 $\in$ A, 9 $\in$ A.

Cho tập B các số tự nhiên là ước của 6, khi đó 1 $\in$ B, 2$\in$ B, 3$\in$ B, 6$\in$ B.

Cho tập C là tập các số tự nhiên lẻ nhỏ hơn 20, khi đó 1 $\in$ C, 3 $\in$ C, 5$\in$ C, 11$\in$ C

b) Xét tập hợp ℕ, khi đó 1 $\in$ ℕ, 4 $\in$ ℕ, - 4 $\notin$ ℕ, $\frac{3}{5}\notin \mathbb{N}$.

Xét tập hợp ℤ, khi đó - 2 $\in$ ℤ, 3 $\in$ ℤ, $\frac{2}{3}\notin \mathbb{Z}$, $\sqrt{10}\notin \mathbb{Z}$.

Xét tập hợp ℚ, khi đó $\frac{2}{3}\in \mathbb{Q}$, $\frac{1}{2}\in \mathbb{Q}$, $\sqrt{2}\notin \mathbb{Q}$, $\sqrt{5}\notin \mathbb{Q}$.

Xét tâp hợp ℝ, khi đó $\sqrt{2}\in ℝ$, 5 $\in$ ℝ. Ta có các tập hợp ℕ, ℤ, ℚ đều là tập hợp con của tập hợp ℝ nên tất cá các phần tử đều thuộc ℝ.

Giải Toán 10 trang 18 Tập 1

Thực hành 2 trang 18 Toán lớp 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử và tìm số phần tử của mỗi tập hợp đó:

a) Tập hợp A các ước của 24;

b) Tập hợp B gồm các chữ số trong số 1 113 305;

c) C = {n ∈ ℕ | n là bội của 5 và n ≤ 30};

d) D = {x ∈ ℝ | x² – 2x + 3 = 0}.

Lời giải:

a) Tập A là tập gồm các ước của 24 nên A = {- 24; - 12; - 8; - 6; - 4; - 3; - 2; - 1; 1; 2; 3; 4; 6; 8; 12; 24}.

Tập A có 16 phần tử

b) Tập B gồm các chữ số trong số 1 113 305 nên B = {0; 1; 3; 5}.

Tập B có 4 phần tử

c) Tập hợp C là tập gồm các số tự nhiên nhỏ hơn hoặc bằng 30 là bội của 5 nên C = {0; 5; 10; 15; 20; 25; 30}.

Tập C có 7 phần tử

d) Xét phương trình x² – 2x + 3 = 0 có ∆ = - 8 < 0. Do đó phương trình vô nghiệm hay không có giá trị x nào thỏa mãn phương trình nên D = $\varnothing$.

Tập D có 0 phần tử

Thực hành 3 trang 18 Toán lớp 10 Tập 1: Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a) A = {1; 3; 5; …; 15};

b) B = {0; 5; 10; 15; 20; …};

c) Tập hợp C các nghiệm của bất phương trình 2x + 5 > 0.

Lời giải:

a) Theo cách chỉ ra tính chất đặc trưng, ta viết:

A = {x | x $\in$ ℕ, x lẻ và x ≤ 15};

b) Theo cách chỉ ra tính chất đặc trưng, ta viết:

B = {x | x $\in$ ℕ, x chia hết cho 5};

c) Theo cách chỉ ra tính chất đặc trưng, ta viết:

C = {x | x $\in$ ℝ, x > $-\frac{5}{2}$}.

Hoạt động khám phá trang 18 Toán lớp 10 Tập 1: Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.

a) A = {-1; 1} và B = {-1; 0; 1; 2};

b) A = ℕ và B = ℤ;

c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này;

d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.

Lời giải:

a) Phần tử của tập hợp A thuộc tập hợp B, vì:

Các phần tử -1 và 1 của tập A đều thuộc tập B.

b) Phần tử của tập hợp A thuộc tập hợp B, vì: tập hợp ℤ là tập gồm các số tự nhiên và các số đối của nó. Vậy tất cả các phần tử của tập số tự nhiên đều thuộc ℤ.

c) Phần tử của tập hợp A thuộc tập hợp B, vì: mỗi học sinh nữ của lớp 10E là một phần tử của tập các học sinh lớp 10E.

d) Phần tử của tập hợp A thuộc tập hợp B, vì: Động vật có xương sống bao gồm cá, động vật lưỡng cư, bò sát, chim và động vật có vú. Vậy tất cả các động vật có vú đều là động vật có xương sống.

Giải Toán 10 trang 19 Tập 1

Thực hành 4 trang 19 Toán lớp 10 Tập 1: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?

a) A = $\left\{\sqrt{3};-\sqrt{3}\right\}$ và B = {x ∈ ℝ | x² – 3 = 0};

b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;

c) E = {x ∈ ℕ | x là ước của 12} và F = {x ∈ ℕ | x là ước của 24}.

Lời giải:

a) Ta có x² – 3 = 0 $\iff \left[\begin{array}{l}x=-\sqrt{3}\\ x=\sqrt{3}\end{array}\right.$

Suy ra $B=\text{{}-\sqrt{3};\sqrt{3}\text{}}$

Tập hợp A là con của tập hợp B, vì các phần tử của tập hợp A đều thuộc tập hợp B; Tập hợp B là con của tập hợp A vì các phần tử của tập hợp B đều thuộc tập hợp A.

Hai tập hợp A và B có bằng nhau vì tập hợp A là tập con của tập hợp B và tập hợp B là tập con của tập hợp A.

b) Tập hợp C là tập con của tập hợp D vì tam giác đều là tam giác cân và có một góc bằng 60⁰ vậy tất cả các tam giác đều thì đều là tam giác cân nên tập hợp C là tập con của tập hợp D.

Hai tập hợp C và D không bằng nhau vì, tam giác đều là tam giác cân nhưng tam giác cân thì chưa chắc là tam giác đều, nên tập hợp C là tập con của tập hợp D nhưng tập hợp D không là tập con của tập hợp C. Vậy hai tập hợp C và D không bằng nhau.

c) Ta có E = {1; 2; 3; 4; 6; 12}; F = {1; 2; 3; 4; 6; 8; 12; 24}

Tập hợp E là con của tập hợp F vì, các phần tử của tập hợp E đều thuộc tập hợp F

Hai tập hợp E và F không bằng nhau vì, tập hợp E là con của tập hợp F nhưng tập hợp F không là con của tập hợp E nên hai tập hợp E và F không bằng nhau.

Thực hành 5 trang 19 Toán lớp 10 Tập 1: Viết tất cả các tập con của tập A = {a; b}.

Lời giải:

Các tập con của tập A gồm: {a}; {b}; {a; b}; $\varnothing$.

Giải Toán 10 trang 20 Tập 1

Vận dụng trang 20 Toán lớp 10 Tập 1: Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu A ⊂ B và B ⊂ C thì A ⊂ C. Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ ven.

Lời giải:

Khẳng định của bạn An là đúng.

Thật vậy, ta có sơ đồ ven sau:

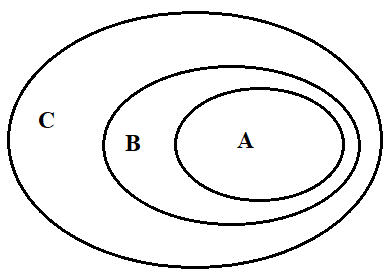
Ta có tập hợp $A\subset B$nên các phần tử của tập hợp A đều thuộc tập hợp B, tập hợp $B\subset C$ nên các phần tử của tập hợp B đều thuộc tâp hợp C. Vậy các phần tử của tập hợp A đều thuộc tập hợp C nên tập hợp $A\subset C$.

Thực hành 6 trang 20 Toán lớp 10 Tập 1: Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:

a) $\left\{x\in ℝ|-2<x<3\right\};$

b) $\left\{x\in ℝ|1\le x\le 10\right\};$

c) $\left\{x\in ℝ|-5<x\le \sqrt{3}\right\};$

d) $\left\{x\in ℝ|\pi \le x<4\right\};$

e) $\left\{x\in ℝ|x<\frac{1}{4}\right\};$

g) $\left\{x\in ℝ|x\ge \frac{\pi }{2}\right\}.$

Lời giải:

a) Xét {x $\in$ ℝ | - 2 < x < 3}$\Rightarrow x\in (-2;3)$.

Vậy {x $\in$ ℝ | - 2 < x < 3} = (-2; 3).

b) Xét {x $\in$ ℝ | 1≤ x ≤ 10}$\Rightarrow x\in \text{[}1;10]$.

Vậy {x $\in$ ℝ | 1≤ x ≤ 10} = [1; 10].

c) Xét {x $\in$ ℝ | - 5 < x ≤ $\sqrt{3}$}$\Rightarrow x\in (-5;\sqrt{3}]$.

Vậy {x $\in$ ℝ | - 5 < x ≤ $\sqrt{3}$}$=(-5;\sqrt{3}]$.

d) Xét {x $\in$ ℝ | π ≤ x < 4}$\Rightarrow x\in \text{[}\pi ;4)$.

Vậy {x $\in$ ℝ | π ≤ x < 4} = [π; 4).

e) Xét {x $\in$ ℝ | x < $\frac{1}{4}$} $\Rightarrow x\in \left(-\infty ;\frac{1}{4}\right)$.

Vậy {x $\in$ ℝ | x < $\frac{1}{4}$} $=\left(-\infty ;\frac{1}{4}\right)$.

g) Xét {x $\in$ ℝ | x ≥ $\frac{\pi }{2}$} $\Rightarrow x\in \left[\frac{\pi }{2};\left.+\infty \right)\right.$.

Vậy {x $\in$ℝ |x ≥ $\frac{\pi }{2}$} $=\left[\frac{\pi }{2};\left.+\infty \right)\right..$

Bài tập

Bài 1 trang 20 Toán lớp 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {x $\in$ ℤ | $\left|x\right|$ < 5};

b) B = {x $\in$ ℝ | 2x² – x – 1 = 0};

c) C = {x $\in$ ℕ | x có hai chữ số}.

Lời giải:

a) Ta có $\left|x\right|$ < 5 ⇔ $\left[\begin{array}{l}x<5\\ x>-5\end{array}\right.$⇔ -5 < x < 5.

Mà x $\in$ ℤ nên x $\in${- 4; - 3; - 2; - 1; 0; 1; 2; 3; 4}.

Vậy A = {- 4; - 3; - 2; - 1; 0; 1; 2; 3; 4}.

b) Ta có: 2x² – x – 1 = 0 ⇔ $\left[\begin{array}{l}x=1\\ x=-\frac{1}{2}\end{array}\right.$

Mà 1; $-\frac{1}{2}$ đều là các số thực.

Vậy B = {1; $-\frac{1}{2}$}.

c) Các số tự nhiên có hai chữ số là 10; 11; 12; …; 99.

Vậy C = {10; 11; 12; …; 99}.

Giải Toán 10 trang 21 Tập 1

Bài 2 trang 21 Toán lớp 10 Tập 1: Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a) Tập hợp A = {1; 2; 3; 6; 9; 18};

b) Tập hợp B các nghiệm của bất phương trình 2x + 1 > 0;

c) Tập hợp C các nghiệm của phương trình 2x – y = 6.

Lời giải:

a) Tập hợp A = {1; 2; 3; 6; 9; 18};

Theo cách chỉ ra tính chất đặc trưng, ta viết:

A = {x ∈ ℕ| x là ước của 18}

b) Tập hợp B các nghiệm của bất phương trình 2x + 1 > 0;

Theo cách chỉ ra tính chất đặc trưng, ta viết

B = {x $\in$ ℝ | x > $-\frac{1}{2}$}.

c) Tập hợp C các nghiệm của phương trình 2x – y = 6.

Theo cách chỉ ra tính chất đặc trưng, ta viết:

C = {(x; y)| x, y $\in$ ℝ, 2x – y = 6}.

Bài 3 trang 21 Toán lớp 10 Tập 1: Trong mỗi cặp tập hợp sau đây, tập hợp nào là con của tập hợp còn lại? Chúng có bằng nhau không?

a) A = {x $\in$ ℕ | x < 2} và B = {x $\in$ ℝ | x² – x = 0};

b) C là tập hợp các hình thoi và D là tập hợp các hình vuông;

c) E = (- 1; 1] và F = (- ∞; 2].

Lời giải:

a) A = {x $\in$ ℕ | x < 2} $\Rightarrow$ A = {0; 1};

B = {x $\in$ ℝ | x² – x = 0} $\Rightarrow$ B = {0; 1};

Vậy tập hợp A là tập con của tập hợp B vì các phần tử của tập hợp A đều thuộc tập hợp B và tập hợp B là tập con của tập hợp A vì các phần tử của tập hợp B đều thuộc tập hợp A.

Hai tập hợp A và B có bằng nhau vì tập hợp A là tập con của tập hợp B và tập hợp B là tập con của tập hợp A.

b) Tập hợp D là con của tập hợp C vì, tất cả các hình vuông đều là hình thoi.

Hai tập hợp C và D không bằng nhau vì tập hợp D là tập con của tập hợp C nhưng tập hợp C không là tập con của tập hợp D (hình thoi chưa chắc là hình vuông)

c) Tâp E là tập con của tập F vì, nửa khoảng từ (- 1; 1] nằm trong nửa khoảng (- ∞; 2].

Hai tập E và F không bằng nhau vì, tập E là tập con của tập F nhưng tập F không là tập con của tập E.

Bài 4 trang 21 Toán lớp 10 Tập 1: Hãy viết tất cả các tập con của tập hợp B = {0; 1; 2}.

Lời giải:

Các tập con của tập B gồm: {0}; {1}; {2}; {0;1}; {0; 2}; {1; 2}; {0; 1; 2}; $\varnothing$.

Bài 5 trang 21 Toán lớp 10 Tập 1: Dùng các kí hiệu đoạn, khoảng, nửa khoảng, viết các tập hợp sau đây:

a) {x $\in$ ℝ | - 2π ≤ x ≤ 2π};

b) {x $\in$ ℝ | $\left|x\right|$ ≤ 3};

c) {x $\in$ ℝ | x < 0};

d {x $\in$ ℝ | 1 – 3x ≤ 0}.

Lời giải:

a) {x $\in$ ℝ | - 2π ≤ x ≤ 2π} $\Rightarrow$ x $\in$ [- 2π; 2π];

Vậy {x $\in$ ℝ | - 2π ≤ x ≤ 2π} = [- 2π; 2π].

b) {x $\in$ ℝ | $\left|x\right|$ ≤ 3} $\Rightarrow$ x $\in$ [- 3; 3];

Vậy {x $\in$ ℝ | $\left|x\right|$ ≤ 3} = [- 3; 3].

c) {x $\in$ ℝ | x < 0} $\Rightarrow$ x $\in$ (- ∞; 0)

Vậy {x $\in$ ℝ | x < 0} = (- ∞; 0).

d) {x $\in$ ℝ | 1 – 3x ≤ 0} = {x $\in$ ℝ | x ≥ $\frac{1}{3}$} $\Rightarrow$ x $\in$ [$\frac{1}{3}$; + ∞}.

Vậy {x $\in$ ℝ | 1 – 3x ≤ 0} = [$\frac{1}{3}$; + ∞}.

Lý thuyết Toán 10 Bài 2: Tập hợp - Chân trời sáng tạo

1. Nhắc lại về tập hợp

- Trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.

- Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa A, B, C, … và kí hiệu phần tử của tập hợp bằng các chữ cái in thường a, b, c, ….

Chú ý: Đôi khi, để ngắn gọn, người ta dùng từ “tập” thay cho “tập hợp”.

- Để chỉ a là một phần tử của tập hợp A, ta viết a ∈ A (đọc là “a thuộc A”). Để chỉ a không là phần tử của tập hợp A, ta viết a ∉ A (đọc là “a không thuộc A”).

Ví dụ 1.

+ Để chỉ 5 là phần tử của tập số tự nhiên ℕ, ta viết 5 ∈ ℕ.

+ Để chỉ - 1 không là phần tử của tập số tự nhiên ℕ, ta viết -1 ∉ ℕ.

- Một tập hợp có thể không chứa phần tử nào. Tập hợp như vậy gọi là tập rỗng, kí hiệu ∅.

- Người ta thường kí hiệu các tập hợp số như sau: ℕ là tập hợp các số tự nhiên, ℤ là tập hợp các số nguyên, ℚ là tập hợp các số hữu tỉ, ℝ là tập hợp các số thực.

Ví dụ 2. Muốn kí hiệu phần tử 5 thuộc tập số tự nhiên, ta kí hiệu: 5 ∈ ℕ.

*Cách xác định tập hợp

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

Chú ý: Khi liệt kê các phần tử của tập hợp, ta có một số chú ý sau đây:

+ Các phần tử có thể được viết theo thứ tự tùy ý.

+ Mỗi phần tử chỉ được liệt kê một lần.

+ Nếu quy tắc xác định các phần tử đủ rõ thì người ta dùng “…” mà không nhất thiết viết ra tất cả các phần tử của tập hợp.

- Có những tập hợp ta có thể đếm hết các phần tử của chúng. Những tập hợp như vậy được gọi là tập hợp hữu hạn.

Ví dụ 3. Cho tập hợp D các số tự nhiên chia hết cho 3 và lớn hơn 3 nhưng nhỏ hơn 10. Mô tả tập hợp D theo hai cách:

Cách 1: Liệt kê phẩn tử tập hợp: D = {6; 9}.

Cách 2: Chỉ ra tính chất đặc trưng của các phẩn tử: D = {n ∈ ℕ | n ⋮ 3, 3 < n < 10}.

2. Tập con và hai tập hợp bằng nhau

- Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A ⊂ B (đọc là A chứa trong B), hoặc B ⊃ A (đọc là B chứa A).

Nhận xét:

+ A ⊂ A và ∅ ⊂ A với mọi tập hợp A.

+ Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B (đọc là A không chứa trong B hoặc B không chứa A).

+ Nếu A ⊂ B hoặc B ⊂ A thì ta nói A và B có quan hệ bao hàm.

- Trong toán học, người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường cong kín, gọi là biểu đồ Ven.

Chú ý: Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu tỉ, tập số thực), ta có quan hệ bao hàm: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.

Ví dụ 4. Cho tập hợp T = {2; 3; 5}; S = {2; 3; 5; 7; 9}; M = {2; 3; 4; 5}.

+ Tập hợp T là tập con của tập hợp S vì tất cả phần tử của T đều có trong phần tử của S.

+ Tập hợp M không là tập hợp con của tập hợp S vì tập M có phần tử 4 không thuộc S.

- Hai tập hợp A và B được gọi là bằng nhau, kí hiệu A = B, nếu A ⊂ B và B ⊂ A.

Ví dụ 5. Cho 2 tập hợp: T = {n ∈ ℕ | n ⋮ 9, 7 < n < 14} và S = {n ∈ ℕ | n ⋮ 3, 8 < n < 10}.

Tìm các phần tử của T và S ta có T = {9} và S = {9} nên T = S.

3. Một số tập con của tập hợp số thực

- Ta thường sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a < b):

Tên gọi và kí hiệu	Tập hợp	Biểu diễn trên trục số
Tập số thực (-∞; +∞)	ℝ
Đoạn [a; b]	{x ∈ ℝ | a ≤ x ≤ b}
Khoảng (a; b)	{x ∈ ℝ | a < x < b}
Nửa khoảng [a; b)	{x ∈ ℝ | a ≤ x < b}
Nửa khoảng (a; b]	{x ∈ ℝ | a < x ≤ b}
Nửa khoảng (-∞; a]	{x ∈ ℝ | x ≤ a}
Nửa khoảng [a; +∞)	{x ∈ ℝ | x ≥ a}
Khoảng (-∞; a)	{x ∈ ℝ | x < a}
Khoảng (a; +∞)	{x ∈ ℝ | x > a}

- Trong các kí hiệu trên, kí hiệu - ∞ đọc là âm vô cực (âm vô cùng), kí hiệu + ∞ đọc là dương vô cực (dương vô cùng).

Ví dụ 6.

Cho x thỏa mãn 2 < x ≤ 6 thì ta kí hiệu x ∈ (2; 6].

Cho x thỏa mãn x ≥ 7 thì ta kí hiệu x ∈ [7; +∞).

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Tập hợp

Trắc nghiệm Bài 2: Tập hợp