Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 67 Tập 1 Chân trời sáng tạo

    Với giải bài tập Toán lớp 10 trang 67 Tập 1 trong Bài 2: Định lí côsin và định lí sin sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 67 Tập 1.

    1 352 21/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 67 Tập 1

    Thực hành 1 trang 67 Toán lớp 10 Tập 1: Tính các cạnh và các góc chưa biết của tam giác ABC trong Hình 4.

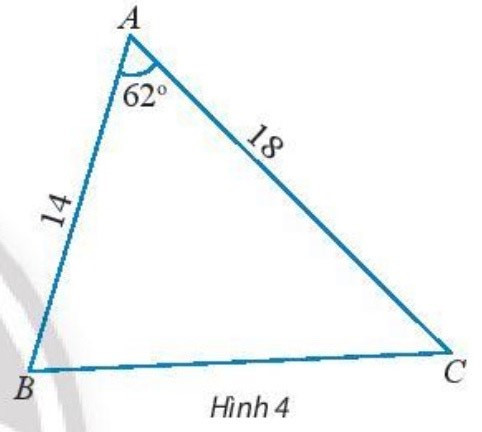
    Giải Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo (ảnh 1)

    Lời giải:

    Theo định lí côsin ta có: BC2=AB2+AC2−2AB.AC.cosA

    =142+182−2.14.18.cos620≈ 283,39

    ⇒BC≈283,39≈16,83

    Theo hệ quả của định lí côsin ta có:

    cosB=AB2+BC2−AC22.AB.BC=142+16,832−1822.14.16,83≈0,3294

    ⇒B^≈70°46'

    ⇒C^≈1800−(A^+B^)≈47015'

    Vận dụng 1 trang 67 Toán lớp 10 Tập 1: Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70° (Hình 5).

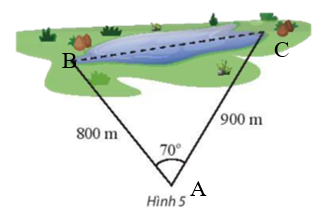
    Giải Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo (ảnh 1)

    Lời giải:

    Gọi A, B, C lần lượt là các điểm tại vị trí người quan sát và hai điểm ở hai đầu hồ nước.

    Áp dụng định lí côsin ta có:

    BC2=AB2+AC2−2AB.AC.cosA

    =8002+9002−2.800.900.cos70° ≈ 957 490,99.

    ⇒ BC ≈ 957 490,99 ≈ 978,5 m

    Vậy khoảng cách giữa hai điểm của một hồ nước là 978,5 m.

    2. Định lí sin trong tam giác

    Hoạt động khám phá 2 trang 67 Toán lớp 10 Tập 1:

    a) Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b; AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD.

    i) Tính sinBDC^  theo a và R.

    ii) Tìm mối liên hệ giữa hai góc BAC^  và BDC^. Từ đó chứng minh rằng 2R = asinA.

    Giải Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo (ảnh 1)

    b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R = asinA.

    Lời giải:

    a)

    i) Vì BD là đường kính nên BCD^=90°.

    Xét tam giác BCD vuông tại C, có:

    sinBDC^=BCBD=a2R        (1)

    ii)

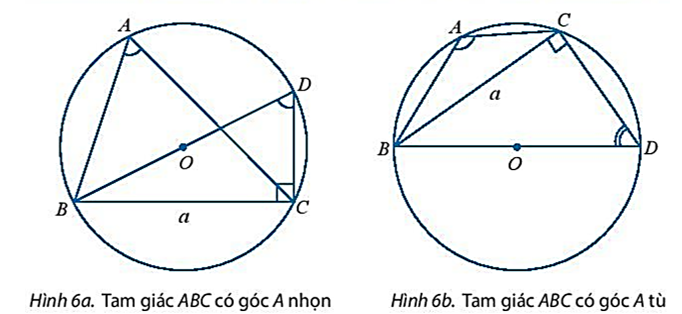
    TH1. Nếu góc A nhọn (Hình 6a) thì:

    Ta có hai góc nội tiếp BAC^ và BDC^cùng chắn cung BC nên BAC^ = BDC^      (2)

    Từ (1) và (2) ta suy ra: sinA=a2R⇒2R=asinA.

    TH2. Nếu góc A tù (Hình 6b) thì:

    Ta có BAC^+BDC^=180°⇒BAC^=180°−BDC^ 

    ⇒ sinBAC^ = sin180°−BDC^=sinBDC^      (3)

    Từ (1) và (3) ta suy ra: sinA=a2R⇒2R=asinA.

    b)

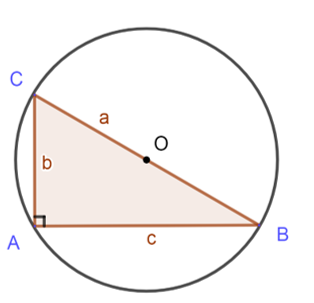
    Giải Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo (ảnh 1)

    Vì tam giác ABC vuông tại A nên tâm của đường tròn ngoại tiếp tam giác ABC là trung điểm của BC nên BC = a = 2R.

    sinA = sin900=1 

    Hay 2R=asinA

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải Toán 10 trang 65 Tập 1

    Giải Toán 10 trang 66 Tập 1

    Giải Toán 10 trang 67 Tập 1

    Giải Toán 10 trang 69 Tập 1

    Giải Toán 10 trang 70 Tập 1

    Giải Toán 10 trang 71 Tập 1

    Giải Toán 10 trang 72 Tập 1

    Giải Toán 10 trang 73 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 3: Giải tam giác và ứng dụng thực tế

    Bài tập cuối chương 4

    Bài 1: Khái niệm vectơ

    Bài 2: Tổng và hiệu của hai vectơ

    Bài 3: Tích của một số với một vectơ

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 352 21/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: