Các dạng bài tập Toán lớp 11 Giữa học kì 1

Các dạng bài tập Toán lớp 11 Giữa học kì 1

A. ĐẠI SỐ VÀ GIẢI TÍCH

Các dạng bài tập Hàm số lượng giác. Phương trình lượng giác

50 bài tập về Tìm tập xác định, tập giá trị của hàm số lượng giác (có đáp án 2022) – Toán 11

50 bài tập về Xét tính chẵn, lẻ, chu kì tuần hoàn của hàm số lượng giác (có đáp án 2022) – Toán 11

50 bài tập về Cách tính GTNN - GTLN của hàm số lượng giác (có đáp án 2022) – Toán 11

50 bài tập về Cách giải phương trình lượng giác cơ bản (có đáp án 2022) – Toán 11

50 bài tập về Phương trình bậc nhất đối với hàm số lượng giác (có đáp án 2022) – Toán 11

50 bài tập về Phương trình bậc hai đối với hàm số lượng giác (có đáp án 2022) – Toán lớp 11

50 bài tập về Phương trình bậc nhất đối với sinx, cosx (có đáp án 2022) – Toán 11

Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết

Công thức giải phương trình lượng giác cơ bản

Công thức, cách biến đổi biểu thức a sinx + b cosx

Công thức, cách gộp nghiệm phương trình lượng giác

Các dạng bài tập Tổ hợp - Xác suất

50 bài tập về Quy tắc đếm (có đáp án 2022) – Toán 11

50 bài tập về Hoán vị, Chỉnh hợp, Tổ hợp (có đáp án 2022) – Toán 11

50 bài tập về Nhị thức Niu-tơn (có đáp án 2022) – Toán 11

50 bài tập về Cách giải phương trình, bất phương trình tổ hợp (có đáp án 2022) – Toán 11

50 bài tập về Xác định biến cố và tính xác suất của biến cố (có đáp án 2022) – Toán 11

Trọn bộ công thức tính xác suất đầy đủ, chi tiết nhất

Công thức hoán vị

Công thức chỉnh hợp

Công thức tổ hợp

Công thức khai triển nhị thức Niu-tơn

Công thức tính tổng các hệ số trong khai triển nhị thức Niu-tơn

Công thức tìm hệ số trong khai triển nhị thức Niu-tơn

Công thức tìm số hạng trong khai triển nhị thức Niu-tơn

Công thức tính xác suất

B. HÌNH HỌC

Các dạng bài tập Phép dời hình và phép đồng dạng trong mặt phẳng

50 bài tập về Phép tịnh tiến (có đáp án 2022) – Toán 11

50 bài tập về Phép đối xứng tâm (có đáp án 2022) – Toán 11

50 bài tập về Phép đối xứng trục (có đáp án 2022) – Toán 11

50 bài tập về Phép quay (có đáp án 2022) – Toán 11

50 bài tập về Phép vị tự (có đáp án 2022) – Toán 11

50 bài tập về Phép đồng dạng (có đáp án 2022) – Toán 11

Công thức phép tịnh tiến

Công thức phép đối xứng tâm

Công thức phép đối xứng trục

Công thức phép quay

Công thức phép vị tự

Công thức phép đồng dạng

Tìm tập xác định, tập giá trị của hàm số lượng giác và cách giải - Toán lớp 11

1. Lý thuyết

a. Hàm số y = sinx

- Tập xác định: D =R

- Tập giá trị: [-1;1]

b. Hàm số y = cosx

- Tập xác định: D =R

- Tập giá trị: [-1;1]

c. Hàm số y = tanx

- Tập xác định: $D=R\backslash \left\{\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right\}$

- Tập giá trị: R

d. Hàm số y = cotx

- Tập xác định: $D=R\backslash \left\{k\pi ,k\in \mathbb{Z}\right\}$

- Tập giá trị: R

2. Các dạng bài tập

Dạng 1. Tìm tập xác định của hàm số lượng giác

- Phương pháp giải:

$y=\frac{f\left(x\right)}{g\left(x\right)}$ xác định khi $g\left(x\right)\ne 0$

$y=\sqrt{f\left(x\right)}$ xác định khi $f\left(x\right)\ge 0$

$y=\frac{f\left(x\right)}{\sqrt{g\left(x\right)}}$ xác định khi g(x) > 0

y = tan[u(x)] xác định khi $u\left(x\right)\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$

y = cot[u(x)] xác định khi $u\left(x\right)\ne k\pi ,k\in \mathbb{Z}$

$\sin x\ne 0$ khi $x\ne k\pi \left(k\in \mathbb{Z}\right)$

$\cos x\ne 0$ khi $x\ne \frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

- Ví dụ minh họa:

Ví dụ 1. Tìm tập xác định của hàm số sau

a) $y=\tan \left(3x+\frac{\pi }{3}\right)$

b) $y=\sqrt{2-\sin x}$

Lời giải

a) $y=\tan \left(3x+\frac{\pi }{3}\right)=\frac{\sin \left(3x+\frac{\pi }{3}\right)}{\cos \left(3x+\frac{\pi }{3}\right)}$

Điều kiện xác định: $\cos \left(3x+\frac{\pi }{3}\right)\ne 0$

$\begin{array}{l}\iff 3x+\frac{\pi }{3}\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\\ \iff 3x\ne \frac{\pi }{6}+k\pi ,k\in \mathbb{Z}\\ \iff x\ne \frac{\pi }{18}+k\frac{\pi }{3},k\in \mathbb{Z}\end{array}$

Vậy tập xác định của hàm số là $D=ℝ\backslash \left\{\frac{\pi }{18}+k\frac{\pi }{3},k\in \mathbb{Z}\right\}$

b) Điều kiện xác định: $2-\sin x\ge 0$

$\iff \sin x\le 2$ (đúng $\forall x\in ℝ$) vì $-1\le \sin x\le 1\forall x\in ℝ$ 

Vậy tập xác định của hàm số là D = R.

Ví dụ 2. Tìm tập xác định của hàm số sau

a) $y=\frac{2}{\sin x-\cos x}$

b) $y=\frac{\tan 3x}{2\sin x+1}+\cot \left(x-1\right)$

Lời giải

a) Điều kiện xác định: $\sin x-\cos x\ne 0\iff \sin x\ne \cos x$ (*)

+ Trường hợp 1: cosx = 0. Ta có sin²x + cos²x = 1

$\iff {\sin }^{2}x=1\iff \sin x=\pm 1$ .

Hiển nhiên $\sin x\ne \cos x$.

+ Trường hợp 2: $\cos x\ne 0$. Chia cả hai vế cho cosx

(*) $\iff \frac{\sin x}{\cos x}\ne 1$$\iff \tan x\ne 1$$\iff x\ne \frac{\pi }{4}+k\pi ;k\in \mathbb{Z}$.

Vậy tập xác định của hàm số là $D=ℝ\backslash \left\{\frac{\pi }{4}+k\pi ;k\in \mathbb{Z}\right\}$

b) Vì $\tan 3x=\frac{\sin 3x}{\cos 3x}$ và $\cot \left(x-1\right)=\frac{\cos \left(x-1\right)}{\sin \left(x-1\right)}$

Điều kiện xác định: $\left\{\begin{array}{l}\cos 3x\ne 0\\ \sin x\ne \frac{-1}{2}\\ \sin \left(x-1\right)\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}3x\ne \frac{\pi }{2}+k\pi \\ x\ne -\frac{\pi }{6}+k2\pi \\ x\ne \frac{7\pi }{6}+k2\pi \\ x-1\ne k\pi \end{array}\right.$$\iff \left\{\begin{array}{l}x\ne \frac{\pi }{6}+\frac{k\pi }{3}\\ x\ne -\frac{\pi }{6}+k2\pi \\ x\ne \frac{7\pi }{6}+k2\pi \\ x\ne 1+k\pi \end{array}\right.$

$\iff \left\{\begin{array}{l}x\ne \frac{\pi }{6}+\frac{k\pi }{3}\\ x\ne 1+k\pi \end{array}\right.(k\in \mathbb{Z})$

Vậy tập xác định của hàm số là $D=ℝ\backslash \left\{\frac{\pi }{6}+\frac{k\pi }{3};1+k\pi ;k\in \mathbb{Z}\right\}$.

Dạng 2. Tìm tập giá trị của hàm số lượng giác

- Phương pháp giải:

Sử dụng tính bị chặn của hàm số lượng giác

$-1\le \sin \left[u\left(x\right)\right]\le 1; 0\le {\sin }^2\left[u\left(x\right)\right]\le 1;$$0\le \left|\sin \left[u\left(x\right)\right]\right|\le 1$

$-1\le \cos \left[u\left(x\right)\right]\le 1;0\le {\cos }^2\left[u\left(x\right)\right]\le 1;$ $0\le \left|\cos \left[u\left(x\right)\right]\right|\le 1$

- Ví dụ minh họa:

Ví dụ 1. Tìm tập giá trị của các hàm số sau:

a) y = 2sin3x – 5

b) $y=2{\sin }^2\left(x^2-\frac{\pi }{12}\right)+5$

c) y = |cos(3x-2)| + 4

Lời giải

a) Ta có: $-1\le \sin 3x\le 1\forall x\in ℝ$

$\begin{array}{l}\iff -2\le 2\sin 3x\le 2\forall x\in ℝ\\ \iff -7\le 2\sin 3x-5\le -3\forall x\in ℝ\end{array}$

Vậy tập giá trị: T = [-7;-3].

b) Ta có: $0\le {\sin }^2\left(x^2-\frac{\pi }{12}\right)\le 1\forall x\in ℝ$

$$$\begin{array}{l}\iff 0\le 2{\sin }^2\left(x^2-\frac{\pi }{12}\right)\le 2\forall x\in ℝ\\ \iff 5\le 2{\sin }^2\left(x^2-\frac{\pi }{12}\right)+5\le 7\forall x\in ℝ\end{array}$

Vậy tập giá trị: T = [5;7].

c) Ta có: $0\le \left|cos\left(3x-2\right)\right|\le 1\forall x\in ℝ$

$\iff 4\le \left|cos\left(3x-2\right)\right|+4\le 5\forall x\in ℝ$

Vậy tập giá trị: T = [4;5].

Ví dụ 2. Tìm tập giác trị của các hàm số sau:

a) $y=\sqrt{\sin x+1}-2$

b) y = cos2x + 4sinx +1

Lời giải

a) Điều kiện xác định: $\sin x+1\ge 0\iff \sin x\ge -1\forall x\in ℝ$.

Tập xác định D = R.

Ta có: $-1\le \sin x\le 1\forall x\in ℝ$

$\begin{array}{l}\iff 0\le \sin x+1\le 2\forall x\in ℝ\\ \iff 0\le \sqrt{\sin x+1}\le \sqrt{2}\forall x\in ℝ\\ \iff -2\le \sqrt{\sin x+1}-2\le \sqrt{2}-2\forall x\in ℝ\end{array}$

Vậy tập giá trị: $T=\left[-2;\sqrt{2}-2\right]$.

b) y = cos2x + 4sinx +1 = 1 - 2sin²x + 4sinx +1 = -2sin²x + 4sinx + 2 = -2(sinx – 1)² + 4.

Ta có: $-1\le \sin x\le 1\forall x\in ℝ$

$\begin{array}{l}\iff -2\le \sin x-1\le 0\forall x\in ℝ\\ \iff 0\le {\left(\sin x-1\right)}^2\le 4\forall x\in ℝ\\ \iff -8\le -2{\left(\sin x-1\right)}^2\le 0\forall x\in ℝ\\ \iff -4\le -2{\left(\sin x-1\right)}^2+4\le 4\forall x\in ℝ\end{array}$

Vậy tập giá trị: T = [-4;4].

Dạng 3. Tìm m để hàm số lượng giác có tập xác định là R

- Phương pháp giải:

$\begin{array}{l}m\ge f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m\ge \underset{x\in \left[a;b\right]}{\max }f\left(x\right)\\ m>f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m>\underset{x\in \left[a;b\right]}{\max }f\left(x\right)\\ m\le f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m\le \underset{x\in \left[a;b\right]}{\min }f\left(x\right)\\ m<f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m<\underset{x\in \left[a;b\right]}{\min }f\left(x\right)\end{array}$

- Ví dụ minh họa:

Ví dụ 1. Tìm m để hàm số $y=\sqrt{\sin x+m}$ xác định trên R.

Lời giải

Để hàm số xác định trên R thì $\sin x+m\ge 0\forall x\in ℝ\iff m\ge -\sin x\forall x\in ℝ$.

Mà ta có $-1\le \sin x\le 1\forall x\in ℝ$

$\iff -1\le -\sin x\le 1\forall x\in ℝ$

Nên $m\ge 1$.

Ví dụ 2. Tìm m để hàm số $y=\sqrt{{\sin }^{2}x-2\sin x+m}$ xác định trên R.

Lời giải

Ta có:$y=\sqrt{{\sin }^{2}x-2\sin x+m}$$=\sqrt{{\left(\sin x-1\right)}^2+m-1}$

Hàm số xác định trên R khi ${\left(\sin x-1\right)}^2+m-1\ge 0\forall x\in ℝ$

$\iff m\ge 1-{\left(\sin x-1\right)}^2\forall x\in ℝ$

Ta có: $-1\le \sin x\le 1\forall x\in ℝ$

$\begin{array}{l}\iff -2\le \sin x-1\le 0\forall x\in ℝ\\ \iff 0\le {\left(\sin x-1\right)}^2\le 4\forall x\in ℝ\\ \iff -4\le -{\left(\sin x-1\right)}^2\le 0\forall x\in ℝ\\ \iff -3\le 1-{\left(\sin x-1\right)}^2\le 1\forall x\in ℝ\end{array}$

Vậy $m\ge 1$.

3. Bài tập tự luyện

Câu 1. Tập xác định của hàm số $y=\cot \left(2x-\frac{\pi }{3}\right)$ là

A. $D=ℝ\backslash \left\{\frac{\pi }{6}+\frac{k\pi }{2};k\in \mathbb{Z}\right\}$

B. $D=ℝ\backslash \left\{\frac{5\pi }{12}+k\pi ;k\in \mathbb{Z}\right\}$

C. $D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$

D. $D=ℝ\backslash \left\{\frac{5\pi }{12}+\frac{k\pi }{2};k\in \mathbb{Z}\right\}$

Câu 2. Tập xác định của hàm số $y=\tan x+\cot x$ là

A. R

B. $ℝ\backslash \left\{k\pi ;k\in \mathbb{Z}\right\}$

C. $ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$

D. $ℝ\backslash \left\{\frac{k\pi }{2};k\in \mathbb{Z}\right\}$

Câu 3. Tập xác định của hàm số $y=\sqrt{\sin x+1}$ là:

A. $D=\left[-1;+\infty \right)$

B. D = R

C. $D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$

D. $D=\left(-\infty ;-1\right]$

Câu 4. Tập xác định của hàm số $y=\frac{3\sin x}{2\cos x-\sqrt{3}}$ là:

A. $D=ℝ\backslash \left\{\frac{\pi }{6}+k2\pi ;k\in \mathbb{Z}\right\}$

B. $D=ℝ\backslash \left\{\frac{\pi }{3}+k2\pi ;k\in \mathbb{Z}\right\}$

C. $D=ℝ\backslash \left\{\pm \frac{\pi }{6}+k2\pi ;k\in \mathbb{Z}\right\}$

D. $D=ℝ\backslash \left\{\frac{\pi }{3}+k2\pi ;\frac{2\pi }{3}+k2\pi ;k\in \mathbb{Z}\right\}$

Câu 5. Tập xác định của hàm số $y=\frac{2021}{1-\tan x}+{\sin }^{2}x$ là

A. $D=ℝ\backslash \left\{\frac{\pi }{4}+k\pi ;\frac{\pi }{2}+k2\pi ;k\in \mathbb{Z}\right\}$

B. $D=ℝ\backslash \left\{\frac{\pi }{4}+k\pi ;\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$

C. $D=ℝ\backslash \left\{\frac{\pi }{4}+k\pi ;k\in \mathbb{Z}\right\}$

D. $D=ℝ\backslash \left\{-\frac{\pi }{4}+k\pi ;-\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$

Câu 6. Tập xác định của hàm số $y=\frac{2x-1}{{\sin }^{2}x-{\cos }^{2}x}$ là

A. $D=ℝ\backslash \left\{\frac{\pi }{4}+k\pi ;k\in \mathbb{Z}\right\}$.

B. $D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$.

C. $D=ℝ\backslash \left\{\frac{\pi }{4}+k\frac{\pi }{2};k\in \mathbb{Z}\right\}$.

D. $D=ℝ\backslash \left\{\frac{3\pi }{4}+k2\pi ;k\in \mathbb{Z}\right\}$.

Câu 7. Tập xác định của hàm số $y=\sqrt{\frac{1-\cos 3x}{1+\sin 4x}}$ là

A. $D=ℝ\backslash \left\{-\frac{\pi }{8}+k\frac{\pi }{2},k\in \mathbb{Z}\right\}$

B. $D=ℝ\backslash \left\{-\frac{3\pi }{8}+k\frac{\pi }{2},k\in \mathbb{Z}\right\}$

C. $D=ℝ\backslash \left\{-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}\right\}$

D. $D=ℝ\backslash \left\{-\frac{\pi }{6}+k\frac{\pi }{2},k\in \mathbb{Z}\right\}$

Câu 8. Hàm số nào dưới đây có tập xác định là R?

A. y = sinx + cot5x

B. $y=\frac{\tan 3x}{{\sin }^{2}x+1}$

C. $y=2\cos \sqrt{x}$

D. $y=\sqrt{1-\sin 2x}$

Câu 9. Tập giá trị của hàm số y = 1 – 2|sin2x| là

A. [1;3] 

B. [-1;1]

C. [-1;3] 

D. [-1;0]

Câu 10. Tập giá trị của hàm số  là

A. [2;3] 

B. [1;2]

C. [2;4]

D. [3;4]

Câu 11. Tập giá trị của hàm số y = 2 + sinxcosx có dạng T = [m,M]. Giá trị của m là:

A. $\frac{5}{2}$

B. $\frac{3}{2}$

C. $\frac{2}{3}$

D. 1

Câu 12. Tập giá trị của hàm số y = 2sin3x +1 là

A. [-1;1]

B. [-5;7]

C. [0;2]

D. [-1;3]

Câu 13. Tìm m để hàm số $y=\frac{2}{\sin x-m}$ xác định trên R.

A. $m\in \left(-\infty ;-1\right)\cup \left(1;+\infty \right)$

B. $m\in \left(-\infty ;-1\right]\cup \left[1;+\infty \right)$

C. $m\ne 1$

D. $m\in \left[-1;1\right]$

Câu 14. Hàm số $y=\frac{2-\sin 2x}{\sqrt{2\cos x+m-1}}$ có tập xác định R khi và chỉ khi:

A. m > 3

B. m < -1

C. $m\ge 3$

D. $m\le -1$

Câu 15. Tìm tất cả các giá trị của tham số m để hàm số $y=\sqrt{{\sin }^{2}x-4\cos x+2m-1}$ có tập xác định là R.

A. $m\ge -\frac{3}{2}$

B. $m\ge \frac{5}{2}$

C. Không có m thỏa mãn

D. $m\ge 5$

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
A	D	B	C	B	C	A	D	B	D	B	D	A	A	B

 

Phép tịnh tiến và cách giải các dạng bài tập - Toán lớp 11

I. Lý thuyết ngắn gọn

1.Trong mặt phẳng cho vectơ $\overrightarrow{v}$. Phép biến hình biến mỗi điểm M thành điểm M′ sao cho $\overrightarrow{MM\text{'}}=\overrightarrow{v}$ được gọi là phép tịnh tiến theo vectơ $\overrightarrow{v}$, ký hiệu $T_{\overrightarrow{v}}$

$T_{\overrightarrow{v}}\left(M\right)=M\text{'}\iff \overrightarrow{MM\text{'}}=\overrightarrow{v}$

2.Trong mặt phẳng tọa độ Oxy, cho điểm M (x; y) và $\overrightarrow{v}=(a;b)$. Khi đó: 

$$\begin{gathered} M\text{'}(x\text{'};y\text{'})=T_{\overrightarrow{v}}\left(M\right)\iff \overrightarrow{MM\text{'}}=\overrightarrow{v} \\ \iff \left\{\begin{array}{l}x\text{'}-x=a\\ y\text{'}-y=b\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=x+a\\ y\text{'}=y+b\end{array}\right. \end{gathered}$$

3.Các tính chất của phép tịnh tiến:

-Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ

-Phép tịnh tiến biến đường thẳng thành đường thằng song song hoặc trùng với nó, biến đoạn thằng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính

II. Các dạng toán phép tịnh tiến

Dạng 1: Xác định ảnh của một hình qua phép tịnh tiến

Phương pháp giải: Sử dụng định nghĩa và các tính chất hoặc biểu thức tọa độ của phép tịnh tiến

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{v}=(3;4)$. Hãy tìm ảnh của điểm A (1; -1) qua phép tịnh tiến theo vectơ $\overrightarrow{v}$

Lời giải

Gọi A′ (x′; y′) là ảnh của điểm A qua phép tịnh tiến theo vectơ $\overrightarrow{v}$

Áp dụng biểu thức tọa độ của phép tịnh tiến: $\left\{\begin{array}{l}x\text{'}=x+a\\ y\text{'}=y+b\end{array}\right.$

Ta có $A\text{'}(x\text{'};y\text{'})=T_{\overrightarrow{v}}\left(A\right)$

$$\begin{gathered} \Rightarrow \left\{\begin{array}{l}x\text{'}=1+3\\ y\text{'}=-1+4\end{array}\right. \\ \iff \left\{\begin{array}{l}x\text{'}=4\\ y\text{'}=3\end{array}\right.\Rightarrow A\text{'}(4;3) \end{gathered}$$

Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{v}=(2;-4)$ và đường thẳng d có phương trình 2x - 3y + 5 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến $T_{\overrightarrow{v}}$

Lời giải

Lấy điểm M (x; y) tùy ý thuộc d, ta có: 2x – 3y + 5 = 0      (1)

Gọi $M\text{'}(x\text{'};y\text{'})=T_{\overrightarrow{v}}\left(M\right)$

$\Rightarrow \left\{\begin{array}{l}x\text{'}=x+2\\ y\text{'}=y-4\end{array}\right.\iff \left\{\begin{array}{l}x=x\text{'}-2\\ y=y\text{'}+4\end{array}\right.$

Thay vào (1) ta được phương trình:

$$\begin{gathered} 2(x\text{'}-2)-3(y\text{'}+4)+5=0 \\ \Rightarrow 2x\text{'}-3y\text{'}-11=0 \end{gathered}$$

Vậy ảnh của d là đường thẳng d’: 2x - 3y – 11 = 0

Dạng 2: Xác định phép tịnh tiến khi biết ảnh và tạo ảnh

Phương pháp giải: Xác định phép tịnh tiến tức là tìm tọa độ của $\overrightarrow{v}$. Để tìm tọa độ của $\overrightarrow{v}$, ta có thể giả sử v = (a; b), sử dụng các dữ kiện trong giả thiết của bài toán để thiết lập hệ phương trình hai ẩn a,b và giải hệ tìm a,b

Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x + y – 9 = 0. Tìm phép tịnh tiến theo vectơ $\overrightarrow{v}$ có giá song song với Oy biến d thành d′ đi qua điểm A (2; 4)

Lời giải

Vì $\overrightarrow{v}$ có giá song song với Oy nên $\overrightarrow{v}=(0;k) k\ne 0$

Lấy $M(x;y)\in \text{d}\Rightarrow \text{3x+y-9=0 }$(1)

Gọi $M\text{'}(x\text{'};y\text{'})=T_{\overrightarrow{v}}\left(M\right)\Rightarrow \left\{\begin{array}{l}x\text{'}=x\\ y\text{'}=y+k\end{array}\right.$

Thay vào (1) ta được: 3x’ + y’ – k – 9 = 0

Do đó $T_{\overrightarrow{v}}\left(d\right)=d\text{'}:3x+y-k-9=0$

Mà A (2; 4) thuộc d, suy ra k=1

Vậy $\overrightarrow{v}=(0;1)$

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d: 2x –3y + 3 = 0 và d′: 2x – 3y – 5 = 0. Tìm tọa độ $\overrightarrow{v}$ có phương vuông góc với d để $T_{\overrightarrow{v}}\left(d\right)=d\text{'}$

Lời giải

Gọi $\overrightarrow{v}=(a;b)$

Lấy điểm M (x; y) tùy ý thuộc d, ta có: d: 2x – 3y + 3 = 0   (1)

Gọi $M\text{'}(x\text{'};y\text{'})=T_{\overrightarrow{v}}\left(M\right)$

Ta có: $\left\{\begin{array}{l}x\text{'}=x+a\\ y\text{'}=y+b\end{array}\right.\iff \left\{\begin{array}{l}x=x\text{'}-a\\ y=y\text{'}-b\end{array}\right.$

Thay vào (1) được: 2x’ - 3y’ - 2a + 3b + 3 = 0

Suy ra: $-2a+3b+3=-5\iff 2a-3b=8$. Chuyển vế sai

Vectơ pháp tuyến của đường thẳng d là $\overrightarrow{n}=(2;-3)$ suy ra vectơ chỉ phương của d là $\overrightarrow{u}=(3;2)$

Suy ra: $\stackrel{\rightharpoonup }{v}.\stackrel{\rightharpoonup }{u}=3a+2b=0$

Có hệ phương trình: $\left\{\begin{array}{l}2a-3b=8\\ 3a+2b=0\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{16}{13}\\ b=\frac{-24}{13}\end{array}\right.$

Vậy $\overrightarrow{v}=\left(\frac{16}{13};\frac{-24}{13}\right)$

Dạng 3: Dùng phép tịnh tiến để giải các bài toán dựng hình

Phương pháp giải:

- Để dựng một điểm M ta tìm cách xem nó là ảnh của một điểm đã biết qua một phép tịnh tiến, hoặc xem M là giao điểm của hai đường trong đó một đường cố định còn một đường là ảnh của một đường đã biết qua phép tịnh tiến

- Sử dụng kết quả: Nếu $T_{\stackrel{\rightharpoonup }{v}}\left(N\right)=M$ và $N\in H$ thì $N\in \left(H\text{'}\right)$, trong đó $(H\text{'})=T_{\overrightarrow{v}}\left(H\right)$ và kết hợp với M thuộc hình (K) để suy ra $M\in \left(H\text{'}\right)\cap \left(K\right)$

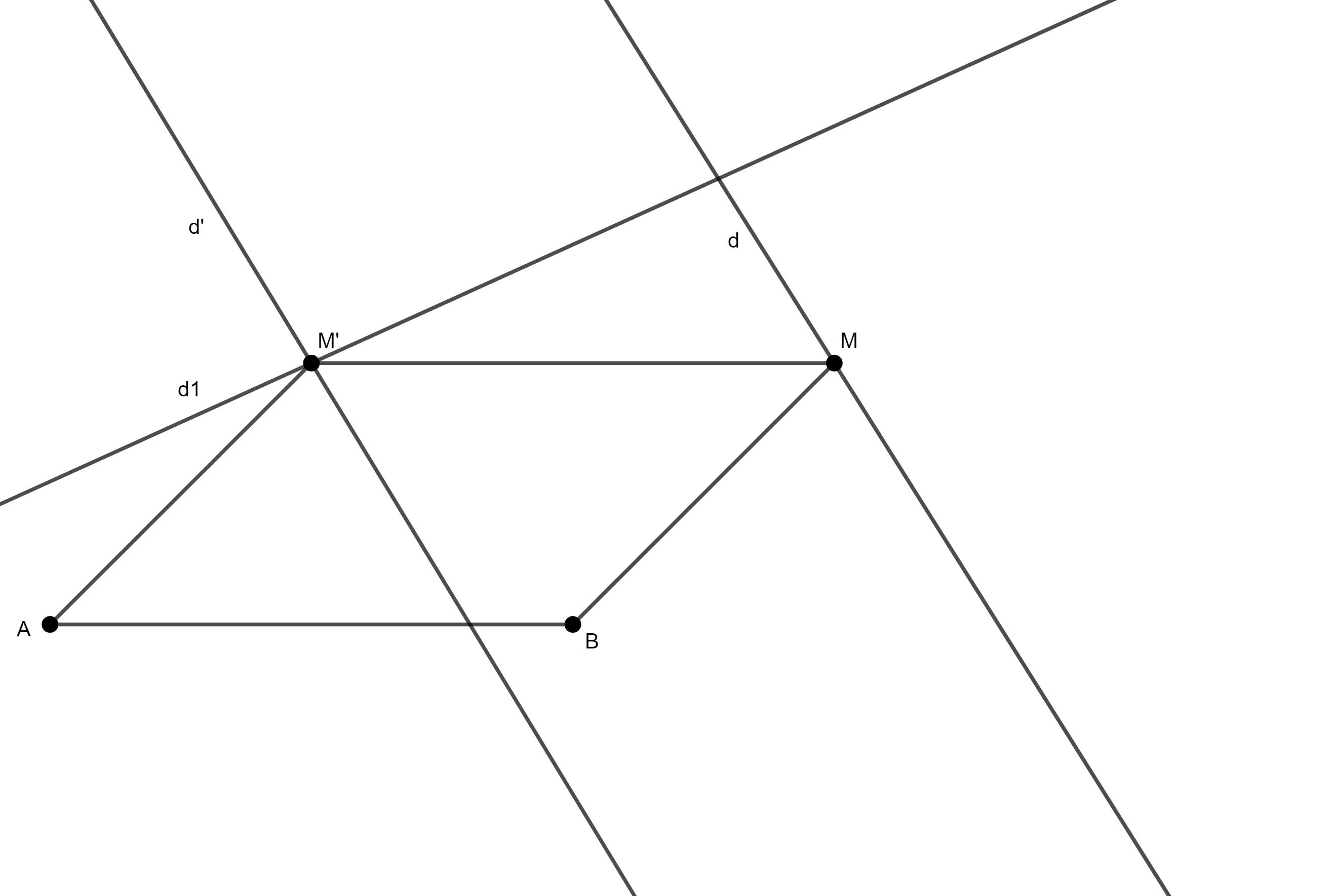
Ví dụ 5:  Trong mặt phẳng cho hai đường thẳng d và d1 cắt nhau và hai điểm A, B không thuộc hai đường thẳng đó sao cho đường thẳng AB không song song hoặc trùng với d (hay d1). Hãy tìm điểm M trên d và điểm M’ trên d1 để tứ giác ABMM’ là hình bình hành

Lời giải:

Điểm M’ là ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{BA}$. Khi đó điểm M’ vừa thuộc d1 vừa thuộc d’ là ảnh của d qua phép tịnh tiến theo vectơ $\overrightarrow{BA}$

Từ đó có thể suy ra cách dựng:

-Dựng d’ là ảnh của d qua phép tịnh tiến theo vectơ $\overrightarrow{BA}$

-M’ là giao điểm của d’ và d1

-Dựng điểm M là ảnh của điểm M’ qua phép tịnh tiến theo vectơ $\overrightarrow{BA}$

Suy ra tứ giác ABMM’ chính là hình bình hành thoả mãn yêu cầu của đầu bài

 

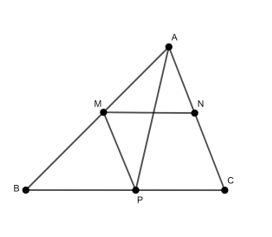
Ví dụ 6: Cho tam giác ABC. Dựng đường thẳng d song song với BC, cắt hai cạnh AB, AC lần lượt tại M, N sao cho AM = CN

Lời giải

Cách dựng:

-Dựng phân giác trong AP của góc A

-Dựng đường thẳng đi qua P song song với AC cắt AB tại M

-Dựng ảnh $N=T_{\overrightarrow{PM}}\left(C\right)$

Đường thẳng MN chính là đường thẳng thỏa yêu cầu bài toán

Dạng 4: Sử dụng phép tịnh tiến để giải bài toán tìm tập hợp điểm

Phương pháp giải: Nếu $T_{\overrightarrow{v}}\left(M\right)=M\text{'}$ và điểm M di động trên hình (H) thì điểm M’ thuộc hình (H’), trong đó (H’) là ảnh của hình (H) qua $T_{\overrightarrow{v}}$

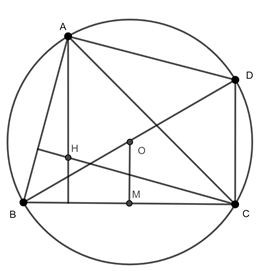
Ví dụ 7: Cho hai điểm phân biệt B và C cố định trên đường tròn (O) tâm O, điểm A di động trên đường tròn (O). Chứng minh rằng khi A di động trên đường tròn (O) thì trực tâm của tam giác ABC di động trên một đường tròn

Lời giải

Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Tia BO cắt đường tròn ngoại tiếp tam giác ABC tại D

$\widehat{BCD}=90°$ nên DC // AH

Tương tự AD // CH

Suy ra: ADCH là hình bình hành

$\overrightarrow{AH}=\overrightarrow{DC}=2\overrightarrow{OM}$

OM không đổi nên H là ảnh của A qua phép tịnh tiến theo vectơ $2\overrightarrow{OM}$. Do đó khi điểm A di động trên đường tròn (O) thì H di động trên đường tròn (O‘) là ảnh của (O) qua phép tịnh tiến theo vectơ $2\overrightarrow{OM}$

Ví dụ 8: Cho tam giác ABC có đỉnh A cố định, $\widehat{BAC}=\alpha$ và $\overrightarrow{BC}=\overrightarrow{v}$ không đổi. Tìm tập hợp các điểm B, C

Lời giải

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó theo định lí sin ta có $\frac{BC}{\sin \alpha }=2R$ không đổi

Vậy $\frac{BC}{2\sin \alpha }=OA=R$ không đổi nên O di động trên đường tròn tâm A bán kính $\frac{BC}{2\sin \alpha }=AO$

Ta có OB = OC = R không đổi và $\widehat{BOC}=2\alpha$ không đổi suy ra $\widehat{OBC}=\widehat{OCB}=\frac{180°-2\alpha }{2}$ không đổi

Mặt khác $\overrightarrow{BC}$ có phương không đổi nên $\overrightarrow{OB},\overrightarrow{OC}$ cũng có phương không đổi

Đặt $\overrightarrow{OB}=\overrightarrow{v_1},\overrightarrow{OC}=\overrightarrow{v_2}$ không đổi thì $T_{\overrightarrow{v_1}}\left(O\right)=B,T_{\overrightarrow{v_2}}\left(O\right)=C$

Vậy tập hợp điểm B là đường tròn $\left(A_1;\frac{BC}{2\sin \alpha }\right)$ ảnh của $\left(A;\frac{BC}{2\sin \alpha }\right)$ qua $T_{\overrightarrow{v_1}}$ và tập hợp điểm C là đường tròn $\left(A_2;\frac{BC}{2\sin \alpha }\right)$ ảnh của $\left(A;\frac{BC}{2\sin \alpha }\right)$ qua $T_{\overrightarrow{v_2}}$

III. Bài tập áp dụng

Bài 1: Cho hai điểm phân biệt B, C cố định trên đường tròn (O) tâm O. Điểm A di động trên (O). Chứng minh khi A di động trên (O) thì trực tâm của tam giác ABC di động trên một đường tròn

Bài 2: Trong mặt phẳng Oxỵ cho đường thẳng d có phương trình 3x – y – 9 = 0. Tìm phép tịnh tiến theo vectơ có phương song song với trục Ox biến d thành đường thẳng d’ đi qua gốc toạ độ và viết phương trình đường thẳng d’

Bài 3: Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C), rồi dựng hình bình hành ABMM’. Tìm tập hợp các điểm M’ khi M di động trên (C)

Bài 4: Trong mặt phẳng toạ độ Oxy cho ba điểm A (-1; -1), B (3; 1), C (2; 3). Xác định toạ độ điểm D sao cho tứ giác ABCD là hình bình hành

Bài 5: Trong mặt phẳng toạ độ Oxy cho đường tròn (C) có phương trình: $x^2+y^2-2x+4y-4=0$. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(-2;3)$

Bài 6: Cho hình bình hành ABCD. Dựng ảnh của tam giác ABC qua phép tịnh tiến theo vectơ $\overrightarrow{AD}$

Bài 7: Cho đường (O) với đường kính AB cố định, một đường kính MN thay đổi. Các đường thẳng AM, AN cắt tiếp tuyến tại B tại P và Q. Tìm quỹ tích trực tâm các tam giác MPQ và NPQ

Bài 8: Tam giác ABC cố định trực tâm H. Vẽ hình thoi BCDE. Từ D và E vẽ các đường vuông góc với AB và AC, các đường thẳng này cắt nhau tại M. Tìm tập hợp điểm M

Bài 9: Trong mặt phẳng với hệ tọa độ Oxy, cho hai parabol $\left(P\right):y=x^2$ và $\left(Q\right):y=x^2+2x+2$.Tìm phép tịnh tiến T biến (Q) thành (P)

Bài 10: Trong mặt phẳng tọa độ Oxy, cho parabol $\left(P\right):y=-x^2+2x+1$. Viết phương trình (P’) sao cho qua phép tịnh tiến theo $\overrightarrow{v}=(1;1)$ thì (P) là ảnh của (P’)

Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:

Hệ thống kiến thức Toán lớp 11 Giữa học kì 1

TOP 30 Đề thi Học kì 1 Toán lớp 11 năm 2022 - 2023 có đáp án

Đề cương Học kì 1 Toán lớp 11 năm 2022 - 2023 chi tiết nhất

Bài tập Toán lớp 11 Học kì 1 có đáp án

Các dạng bài tập Toán lớp 11 Học kì 1