Hệ thống kiến thức Toán lớp 11 Học kì 2

Hệ thống kiến thức Toán lớp 11 Học kì 2

Đề thi Toán lớp 11 học kì 2 năm 2022 - 2023 có đáp án 

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng học kì 2

Năm học 2022 - 2023

Môn: Toán 11

Thời gian làm bài: 45 phút

Đề thi Toán lớp 11 học kì 2 năm 2022 - 2023 có đáp án Đề số 1

I. PHẦN TRẮC NGHIỆM ( 6 điểm)

Câu 1: Cho hàm số $y=\frac{-x^2+2x-3}{x-2}.$ Đạo hàm y’ của hàm số là biểu thức nào sau đây?

A. $-1-\frac{3}{{(x-2)}^2}$

B. $1+\frac{3}{{(x-2)}^2}$

C. $-1+\frac{3}{{(x-2)}^2}$

D. $1-\frac{3}{{(x-2)}^2}$

Câu 2. Cho dãy số (u_n) xác định bởi $u_n=\frac{2^n.\sin n}{9^n}$. Tính lim u_n

A. 0

B. $\frac{2}{9}$

C. $+\infty$

D. $\frac{9}{2}$

Câu 3. Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và $SA\perp \left(ABCD\right)$. Biết Tính góc giữa SC và mp (ABCD).

A. 30^o

B. 45^o

C. 60^o

D. 75^o

Câu 4. Cho hình lập phương ABCD.A’B’C’D’. Hệ thức nào sau đây đúng?

A. $\overrightarrow{AC\text{'}}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AA\text{'}}$

B. $\overrightarrow{AC\text{'}}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{AA\text{'}}$

C. $\overrightarrow{AC\text{'}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA\text{'}}$

D. $\overrightarrow{AC\text{'}}=\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{AA\text{'}}$

Câu 5. Viết phương trình tiếp tuyến kẻ từ điểm A(2; 3) tới đồ thị hàm số $y=\frac{3x+\text{}4}{x-1}$ là

A. y = - 28x + 59; y = x+ 1

B. y = -24x + 51; y = x+ 1.

C. y = -28x+ 59

D. y= -28x + 59; y = -24x + 51.

Câu 6. Cho hàm số $f\left(x\right)=x^3-3x+2018$. Tập nghiệm của bất phương trình $f\text{'}\left(x\right)>0$ là:

A. (-1; 1)

B. [-1; 1]

C. $\left(-\infty -1\right)\cup \left(1;+\infty \right)$

D. $\left(-\infty ;-1\right]\cup \left[1;+\infty \right)$

Câu 7: Tìm m để các hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2+mx+2m+1}{x+1}\text{ khi }x\ge 0\\ \frac{2x+3m-1}{\sqrt{1-x}+2}\text{ khi }x<0\end{array}\right.$có giới hạn khi $x\to 0$

A. $m=\frac{1}{3}$

B. $m=-\frac{1}{3}$

C. $m=-\frac{2}{3}$

D. $m=-\frac{4}{3}$

Câu 8: Giới hạn $\underset{x\to 2}{\lim }\frac{\sqrt{x+2}-\sqrt{8-2x}}{x-2}$ bằng:

A. $+\infty$

B. $-\infty$

C. 0

D. $\frac{3}{4}$

Câu 9. Tìm a, b để hàm số $f\left(x\right)=\left\{\begin{array}{l}{x}^2+1khix\ge 0\\ 2x^2+ax+bkhix<0\end{array}\right.$có đạo hàm tại x= 0?

A. a = 10,  b= 11

B. a = 0, b = -1

C. a = 0, b = 1

D. a= 20, b = 1

Câu 10: Cho hình chóp S.ABC có SA= SB = SC và $\widehat{ASB}=\widehat{BSC}=\widehat{CSA}$. Hãy xác định góc giữa cặp vectơ $\overrightarrow{SB}$ và $\overrightarrow{AC}$?

A. 60^o

B. 120^o

C. 45^o

D. 90^o

Câu 11. Cho hình chóp S.ABCD có $SA\perp \left(ABCD\right)$ và $\Delta ABC$ vuông ở B, AH là đường cao của $\Delta ABC$. Khẳng định nào sau đây sai?

A. $SA\perp BC$

B. $AH\perp BC$

C. $AH\perp AC$

D. $AH\perp SC$

Câu 12: Giới hạn $\underset{x\to -\infty }{\lim }\left(-x^2-10x^5-10x\right)$ bằng:

A. $+\infty$

B. $-\infty$

C. 1

D. -4

Câu 13: Đạo hàm của hàm số $f\left(x\right)={\left(\frac{2x+1}{x+1}\right)}^{2018}$ là:

A. $f\text{'}\left(x\right)=2018{\left(\frac{2x+1}{x+1}\right)}^{2017}\left(\frac{-1}{x+1}\right)$

B. $f\text{'}\left(x\right)=2018\frac{{\left(2x+1\right)}^{2017}}{{\left(x+1\right)}^{2019}}$

C. $f\text{'}\left(x\right)=2018{\left(\frac{2x+1}{x+1}\right)}^{2017}$

D. $f\text{'}\left(x\right)={\left(\frac{2x+1}{x+1}\right)}^{2017}{\left(\frac{1}{x+1}\right)}^2$

Câu 14: Cho hàm số $y=k{x}^3+\text{}\sqrt{x^2+x-2}$. Với giá trị nào của k thì $y\text{'}\left(2\right)=\frac{53}{4}$?

A. k = -1

B. k = 1

C. k = -2

D. k = 3

Câu 15. Cho chuyển động thẳng xác định bởi phương trình $s=t^3-3t^2-9t+2$ (t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng?

A. Vận tốc của chuyển động bằng  khi t = 0 hoặc t=2.

B. Vận tốc của chuyển động tại thời điểm t = 2  là v = 18m/s.

C. Gia tốc của chuyển động tại thời điểm t = 3 là a= 12m/s2.

D. Gia tốc của chuyển động bằng 0 khi t = 0.

Câu 16: Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:

A. 60^o

B. 90^o

C. 45^o

D. 30^o

Câu 17. Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$, M là trung điểm của BB’. Đặt $\overrightarrow{CA}=\overrightarrow{a}, \overrightarrow{CB}=\overrightarrow{b}, \overrightarrow{A{A}^{\text{'}}}=\overrightarrow{c}$. Khẳng định nào sau đây đúng?

A. $\overrightarrow{AM}=\overrightarrow{b}+\overrightarrow{c}-\frac{1}{2}\overrightarrow{a}$

B. $\overrightarrow{AM}=\overrightarrow{a}-\overrightarrow{c}+\frac{1}{2}\overrightarrow{b}$

C. $\overrightarrow{AM}=\overrightarrow{a}+\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}$

D. $\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c}$

Câu 18: Giá trị của $C=\lim \frac{{\left(2n^2+1\right)}^4{\left(n+2\right)}^9}{n^{17}+1}$ bằng:

A. $+\infty$

B. $-\infty$

C. 16

D. 1

Câu 19: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Tan của góc giữa mặt bên và mặt đáy bằng:

A. $\sqrt{2}$

B. $\frac{\sqrt{2}}{2}$

C. $\frac{\sqrt{3}}{2}$

D. $\sqrt{3}$

Câu 20. Cho hàm số $y=\frac{ax+b}{x-2}$, có đồ thị là (C). Tìm a, b biết tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox có phương trình là $y=\frac{-1}{2}x+2$?

A. a= -1, b= 1

B. a= -1, b = 2

C. a= -1, b = 3

D. a= -1, b = 4

II. PHẦN TỰ LUẬN (4 điểm)

Câu 1: Tìm các giới hạn sau:

a) $\underset{x\to 1}{\lim }\frac{3{\text{x}}^2-2\text{x}-1}{x^3-1}$

b) $\underset{x\to 1}{\lim }\frac{3{\text{x}}^2-2\text{x}-1}{x^3-1}$

c) $\underset{x\to 1}{\lim }\frac{3{\text{x}}^2-2\text{x}-1}{x^3-1}$

Câu 2: Xét tính liên tục của hàm số sau tại điểm x₀ = 2?

$f\left(x\right)=\left\{\begin{array}{l}\frac{2{\text{x}}^2-3\text{x}-2}{2\text{x}-4}khix\ne 2\\ \frac{3}{2}khix=2\end{array}\right.$

Câu 3. Cho hàm số $y=f\left(x\right)=-x^3-3{\text{x}}^2+9\text{x}+2011$ có đồ thị (C).

a) Giải bất phương trình: $f{}^{\text{'}}\left(x\right)\le 0$

b) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 1.

Câu 4: Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a  và khoảng cách từ điểm D đến đường thẳng BC là a. Gọi H là trung điểm BC, I là trung điểm AH.

a) Chứng minh rằng đường thẳng BC vuông góc với mặt phẳng (ADH) và DH = a.

b) Chứng minh rằng đường thẳng DI vuông góc với mặt phẳng (ABC).

c) Tính khoảng cách giữa AD và BC

Đáp án và lời giải Đề số 1 

1. C	2. A	3. A	4. C	5. C	6. C	7. D	8. D	9. C	10. D
11. C	12. A	13. D	14. B	15. C	16. B	17. D	18. C	19. A	20. D

I. PHẦN TRẮC NGHIỆM

Câu 1: Đáp án C

Cách 1: Ta có

$$\begin{gathered} y^{\text{'}}=\frac{{\left(-x^2+2x-3\right)}^{\text{'}}\left(x-2\right)-\left(-x^2+2x-3\right){\left(x-2\right)}^{\text{'}}}{{\left(x-2\right)}^2} \\ =\frac{\left(-2x+2\right)\left(x-2\right)-\left(-x^2+2x-3\right).1}{{\left(x-2\right)}^2}=\frac{-x^2+4x-1}{{\left(x-2\right)}^2}=-1+\frac{3}{{\left(x-2\right)}^2} \end{gathered}$$

Cách 2: Ta có:

$y=\frac{-x^2+2x-3}{x-2}=-x-\frac{3}{x-2}$ $\Rightarrow y\text{'}=-1+\text{}\frac{3}{{(x-2)}^2}$

Câu 2: Đáp án A

Theo công thức giới hạn đặc biệt, ta có:

$\left|\frac{2^n.\sin n}{9^n}\right|\le \frac{2^n}{9^n}={\left(\frac{2}{9}\right)}^n$

Mà $lim{\left(\frac{2}{9}\right)}^n=0$ nên lim u_n = 0.

Câu 3: Đáp án A.

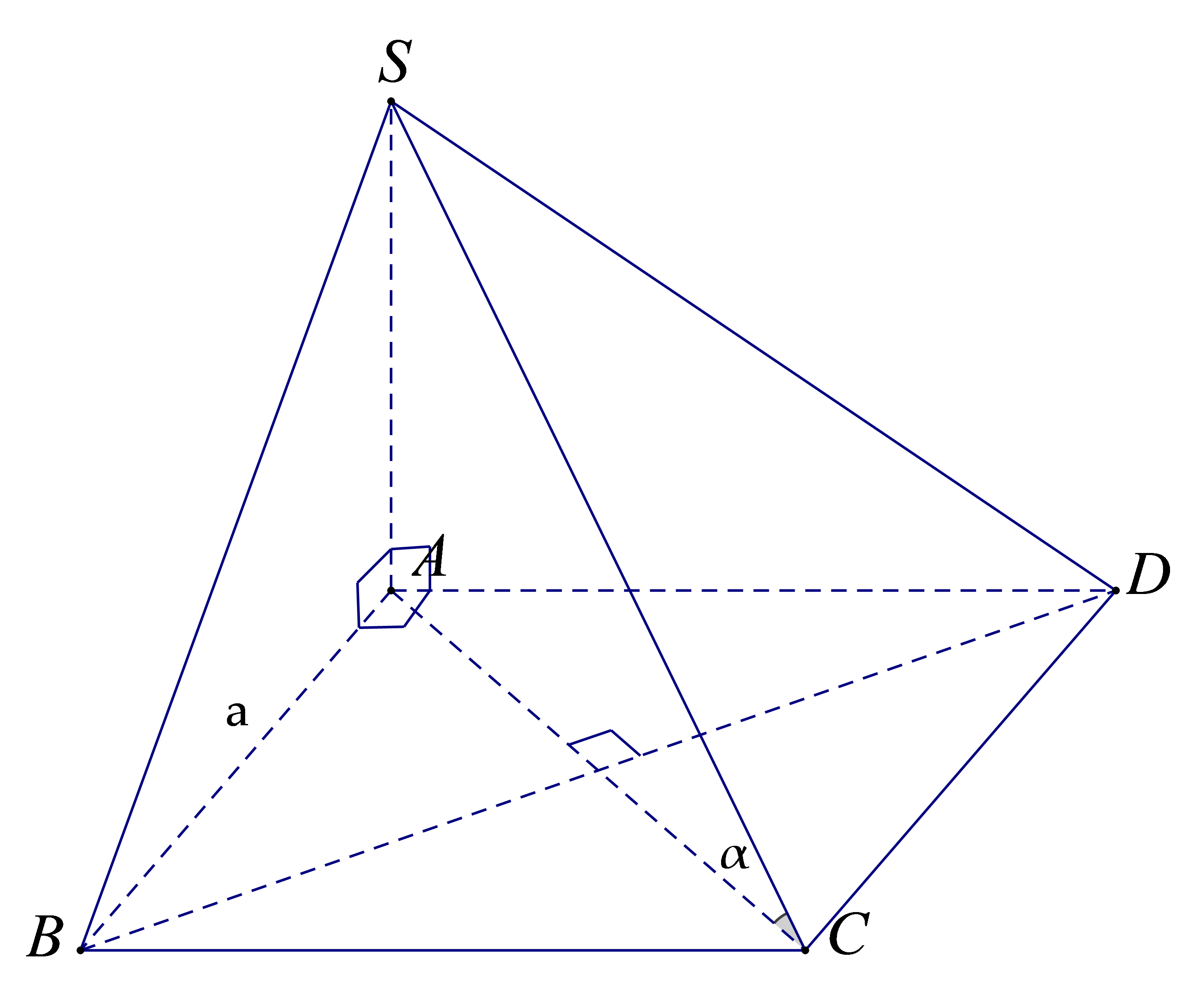
Ta có: $SA\perp \left(ABCD\right)\Rightarrow SA\perp AC$

$\Rightarrow \widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{SCA}=\alpha$

Vì ABCD là hình vuông cạnh a

$\Rightarrow AC=a\sqrt{2},SA=\frac{a\sqrt{6}}{3}$

$\Rightarrow \tan \alpha =\frac{SA}{AC}=\frac{\sqrt{3}}{3}\Rightarrow \alpha =30°$.

Câu 4: Đáp án C.

Phương pháp:

Sử dụng công thức ba điểm và các vectơ bằng nhau.

Cách giải:

Ta có: $\overrightarrow{AC\text{'}}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC\text{'}}.$

Mà $\overrightarrow{BC}=\overrightarrow{AD},\overrightarrow{CC\text{'}}=\overrightarrow{AA\text{'}}\Rightarrow \overrightarrow{AC\text{'}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA\text{'}}.$

Câu 5: Đáp án C.

$y=\frac{3x+\text{}4}{x-1}\widehat{\text{}}\Rightarrow y\text{'}=\frac{-7}{{(x-1)}^2}$

Phương trình tiếp tuyến của đồ thị (C) $y=\frac{3x+\text{}4}{x-1}$ tại điểm $M(x_0;y_0)\in \left(C\right)\text{}$ với $x_0\ne 2$ là:

$y=y\text{'}\left(x_0\right)(x-x_0)+y_0\iff y=\frac{-7}{{(x_0-1)}^2}(x-x_0)+\frac{3x_0+4}{x_0-1}$ (*)

Vì tiếp tuyến đi qua điểm A(2; 3) nên ta có:

$$\begin{gathered} 3=\frac{-7}{{(x_0-1)}^2}(x-x_0)+\frac{3x_0+4}{x_0-1} \\ \begin{array}{l}\Rightarrow 3=-7(2-x_0)+\text{}(3x_0+4)(x_0-1)\\ \iff 3x_0^2-6x_0+\text{}3=-14+\text{}7x_0+\text{}3x_0^2-3x_0+4x_0-4\\ \iff -14x_0=-21\iff x_0=\frac{3}{2}\Rightarrow y_0=17\end{array} \end{gathered}$$

Và $y\text{'}\left(x_0\right)=-28$

Vậy có một tiếp tuyến thỏa đề bài là: $y=-28\left(x-\frac{3}{2}\right)+\text{}17$ hay y = -28x + 59.

Câu 6: Đáp án C.

Phương pháp:

+) Tính $f\text{'}\left(x\right).$

+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.

Cách giải:

Ta có: $f\text{'}\left(x\right)=3x^2-3>0\iff x^2-1>0\iff \left[\begin{array}{l}x>1\\ x<-1\end{array}\right.$

Vậy tập nghiệm của bất phương trình là $\left(-\infty -1\right)\cup \left(1;+\infty \right).$

Câu 7: Đáp án D.

Ta có:  $$\begin{gathered} \underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\frac{x^2+mx+2m+1}{x+1}=2m+1 \\ \underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\frac{2x+3m-1}{\sqrt{1-x}+2}=\frac{3m-1}{3} \end{gathered}$$

Hàm số có giới hạn khi $x\to 0$ khi và chỉ khi $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)$

Câu 8: Đáp án D.

Phương pháp:

Nhân cả tử và mẫu với biểu thức liên hợp của tử.

Cách giải:

Ta có:

 $$\begin{gathered} \underset{x\to 2}{\lim }\frac{\sqrt{x+2}-\sqrt{8-2x}}{x-2}=\underset{x\to 2}{\lim }\frac{x+2-8+2x}{\left(x-2\right)\left(\sqrt{x+2}+\sqrt{8-2x}\right)} \\ =\underset{x\to 2}{\lim }\frac{3\left(x-2\right)}{\left(x-2\right)\left(\sqrt{x+2}+\sqrt{8-2x}\right)}=\underset{x\to 2}{\lim }\frac{3}{\sqrt{x+2}+\sqrt{8-2x}} \\ =\frac{3}{\sqrt{2+2}+\sqrt{8-2.2}}=\frac{3}{2+2}=\frac{3}{4} \end{gathered}$$

Chú ý: HS có thể sử dụng chức năng CALC trên MTCT để tìm giới hạn của hàm số.

Câu 9: Đáp án C.

Để hàm số đã cho có đạo hàm tại x = 0 khi và chỉ khi:

+ Hàm số liên tục tại x= 0

+Đạo hàm bên trái và đạo hàm bên phải tại điểm x = 0 bằng nhau.

+) Ta có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }(\text{}{x}^2+1)=1;\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }(2x^2+\text{}ax+b)=b$

Do đó, để hàm số liên tục tại x = 0 khi b = 1 .

+)  Ta có:  f(0) = 1

$\begin{array}{l}f\text{'}\left(0^{+}\right)=\underset{x\to 0^{+}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=\underset{x\to 0^{+}}{\lim }\frac{x^2+\text{}1-1}{x}=\underset{x\to 0^{+}}{\lim }x=0;\\ f\text{'}\left(0^{-}\right)=\underset{x\to 0^{-}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=\underset{x\to 0^{-}}{\lim }\frac{2x^2+\text{}ax+1-1}{x}=\underset{x\to 0^{-}}{\lim }(2x+a)=a\end{array}$

$\Rightarrow f\text{'}\left(0^{+}\right)=f\text{'}\left(0^{-}\right)\iff a=0$

Vậy a= 0,  b =1 là những giá trị cần tìm.

Câu 10: Đáp án D

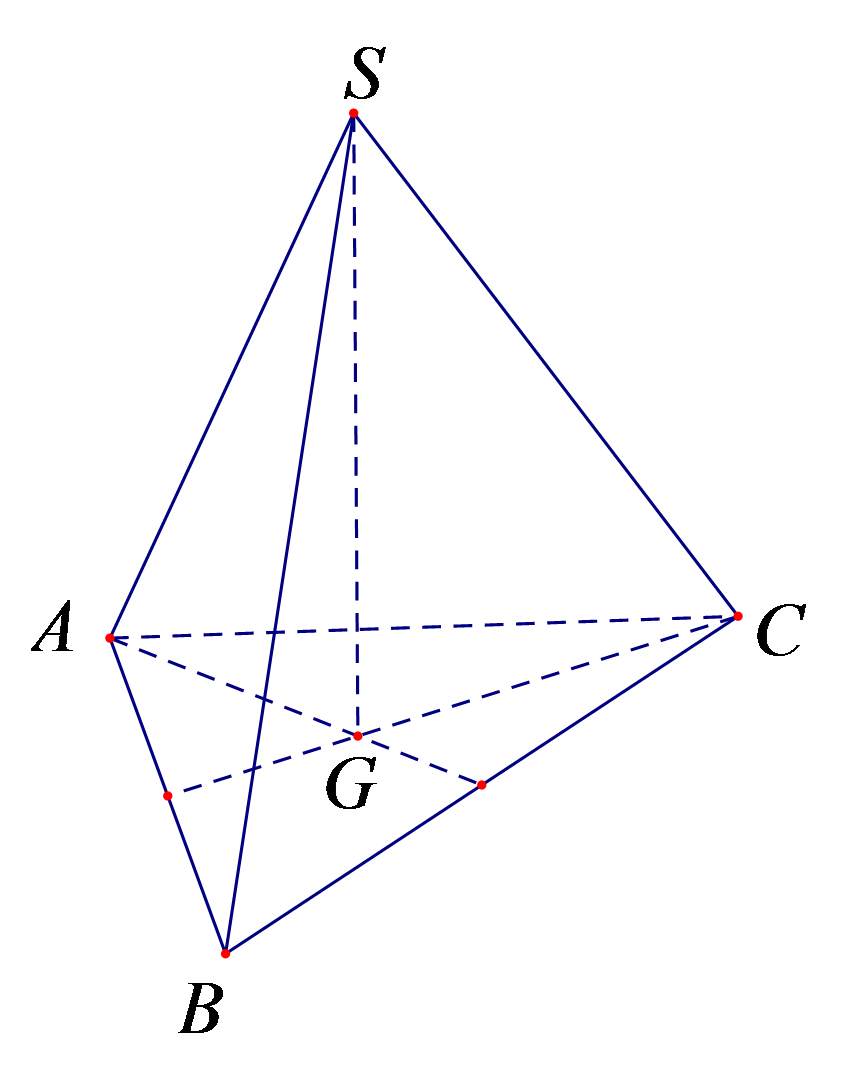
 Ta có SA= SB = SC nên $\Delta SAB=\Delta SBC=\Delta SCA\left(c-g-c\right)$

Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.

Vì hình chóp S.ABC có SA=  SB = SC nên hình chiếu của S trùng với G.

Hay $SG\perp \left(ABC\right)$

Ta có: $\left\{\begin{array}{l}AC\perp BG\\ AC\perp SG\end{array}\right.\Rightarrow AC\perp \left(SBG\right)$

Suy ra $AC\perp SB$

Vậy góc giữa cặp vectơ $\overrightarrow{SB}$ và $\overrightarrow{AC}$ bằng 90⁰.

Cách 2:

SB  và AC

Ta có: $\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.\left(\overrightarrow{SC}-\overrightarrow{SA}\right)=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}$

$=SB.SC\cos \widehat{BSC}-SB.SA.\cos \widehat{ASC}=0$

Vì SA= SB = SC và $\widehat{BSC}=\widehat{ASC}$

Do đó: $\left(\overrightarrow{SB},\overrightarrow{AC}\right)={90}^0$

Câu 11: Đáp án C.

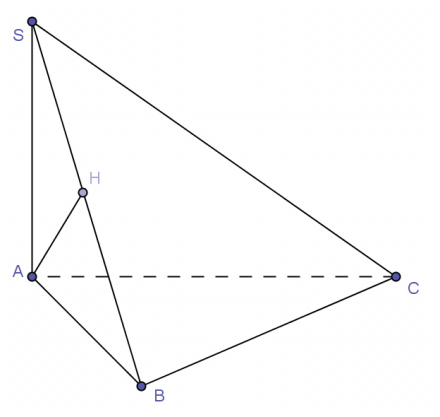
+) Do $SA\perp \left(ABCD\right)\Rightarrow SA\perp BC$ nên câu A đúng.

+) Tam giác ABC vuông ở B nên $AB\perp BC$

Lại có: $SA\perp BC$ ( vì $SA\perp \left(ABCD\right)$)

Do đó: $BC\perp \left(SAB\right)\Rightarrow AH\perp BC$

nên câu B.

+) Theo trên ta có: $\left\{\begin{array}{c}AH\perp BC\\ AH\perp SB\end{array}\right.\Rightarrow AH\perp \left(SBC\right)\Rightarrow AH\perp SC$

=> D đúng.

Vậy câu C sai.

Câu 12: Đáp án A.

Ta có:

$\begin{array}{l}\underset{x\to -\infty }{\lim }\left(-x^2-10x^5-10x\right)=\underset{x\to -\infty }{\lim }{x}^5\left(\frac{-1}{x^3}-10-\frac{10}{x^4}\right)=+\infty \\ \underset{x\to \infty }{\lim }{x}^5=-\infty ;\underset{x\to -\infty }{\lim }\left(\frac{-1}{x^3}-10-\frac{10}{x^4}\right)=-10<0\end{array}$

Câu 13: Đáp án D.

Phương pháp:

Sử dụng công thức tính đạo hàm của hàm hợp $\left(u^n\right)\text{'}=n.u^{n-1}.u\text{'}$ và công thức tính nhanh $\left(\frac{ax+b}{cx+d}\right)\text{'}=\frac{ad-bc}{{\left(cx+d\right)}^2}.$

Cách giải:

Ta có: $f\text{'}\left(x\right)=2018{\left(\frac{2x+1}{x+1}\right)}^{2017}.\left(\frac{2x+1}{x+1}\right)\text{'}=2018{\left(\frac{2x+1}{x+1}\right)}^{2017}.\frac{1}{{\left(x+1\right)}^2}=2018\frac{{\left(2x+1\right)}^{2017}}{{\left(x+1\right)}^{2019}}$

Câu 14: Đáp án B

Ta có:

$\begin{array}{l}y\text{'}=(k{x}^3+\text{}\sqrt{x^2+x-2})\text{'}\\ =3k{x}^2+\text{}\frac{(x^2+x-2)\text{'}}{2\sqrt{x^2+x-2}}=3k{x}^2+\frac{2x+1}{2\sqrt{x^2+x-2}}\\ \Rightarrow y\text{'}\left(2\right)=12k+\frac{5}{4}\end{array}$

Để $y\text{'}\left(2\right)=\frac{53}{4}$ thì $y\text{'}\left(2\right)=12k+\frac{5}{4}=\frac{53}{4}$

$\iff 12k=12\iff k=1$

Câu 15: Đáp án C.

Phương trình vận tốc của chuyển động là:

$\begin{array}{l}v\left(t\right)=s\text{'}\left(t\right)=3t^2-6t-9\\ \Rightarrow v\left(t\right)=0\iff t=3\end{array}$

Phương trình  gia tốc của chuyển động là:

$a\left(t\right)=s"\left(t\right)=6t-6,(m/s^2)$

$\Rightarrow a\left(3\right)=12$ và a(t) = 0 khi  t = 1 .

Câu 16: Đáp án B.

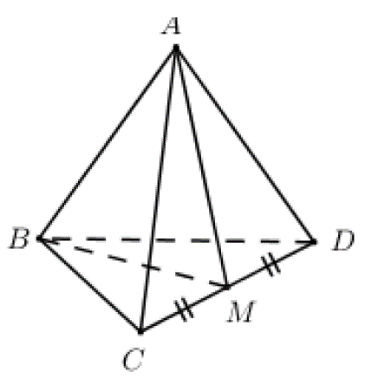
Phương pháp:

Tứ diện đều có các cặp cạnh đối vuông góc.

Cách giải:

Gọi M là trung điểm của CD ta có:

$\Delta BCD$ đều $\Rightarrow BM\perp CD$, $\Delta ACD$ đều $\Rightarrow AM\perp CD.$

Ta có: $\left\{\begin{array}{l}CD\perp AM\\ CD\perp BM\end{array}\right.\Rightarrow CD\perp \left(ABM\right)\supset AC\Rightarrow CD\perp AB\Rightarrow \angle \left(AB;CD\right)={90}^0$

Câu 17: Đáp án D.

Ta phân tích như sau:

$$\begin{gathered} \overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{CB}-\overrightarrow{CA}+\frac{1}{2}\overrightarrow{B{B}^{\text{'}}} \\ =\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c} \end{gathered}$$

Câu 18: Đáp án C.

Ta có: $C=\lim \frac{n^8{(2+\frac{1}{n^2})}^4.n^9{(1+\frac{2}{n})}^9}{n^{17}(1+\frac{1}{n^{17}})}=\lim \frac{{(2+\frac{1}{n^2})}^4.{(1+\frac{2}{n})}^9}{1+\frac{1}{n^{17}}}=16$

Câu 19: Đáp án A.

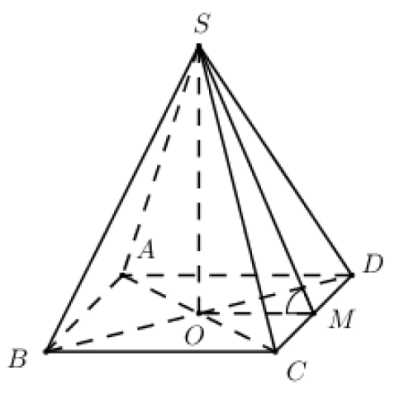
Phương pháp:

+) Xác định góc giữa mặt bên và đáy là góc giữa hai đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng đó.

+) Tính tan của góc xác định được.

Cách giải:

Gọi $O=AC\cap BD.$ Do S.ABC là chóp đều $\Rightarrow SO\perp \left(ABCD\right).$

Gọi M là trung điểm của CD ta có: OM là đường trung bình của tam giác $BCD\Rightarrow OM//BC.$

$\Rightarrow OM\perp CD.$

Ta có: $\left\{\begin{array}{l}CD\perp OM\\ CD\perp SO\left(SO\perp \left(ABCD\right)\right)\end{array}\right.\Rightarrow CD\perp \left(SOM\right)\Rightarrow CD\perp SM.$

$\left\{\begin{array}{l}\left(SCD\right)\cap \left(ABCD\right)=CD\\ \left(SCD\right)\supset SM\perp CD\\ \left(ABCD\right)\supset OM\perp CD\end{array}\right.\Rightarrow \angle \left(\left(SCD\right);\left(ABCD\right)\right)=\angle \left(SM;OM\right)=\angle SMO.$

Ta có $OM=\frac{a}{2}.\Delta SCD$ đều cạnh $a\Rightarrow SM=\frac{a\sqrt{3}}{2}.$

Áp dụng định lý Pytago trong tam giác vuông $SOM$ ta có:

$$\begin{gathered} SO=\sqrt{S{M}^2-O{M}^2}=\sqrt{\frac{3a^2}{4}-\frac{a^2}{4}}=\frac{a\sqrt{2}}{2}. \\ \Rightarrow \tan \angle SMO=\frac{SO}{OM}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a}{2}}=\sqrt{2}. \end{gathered}$$

Câu 20: Đáp án D.

Ta có: $y\text{'}=\frac{-2a-b}{{(x-2)}^2}$

+) Giao điểm của tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox là $A\left(\frac{-b}{a};0\right)$.

+) Tiếp tuyến tại A có phương trình: $y=-\frac{1}{2}x+2$

$A\in d\Rightarrow 0=\frac{-1}{2}.\frac{-b}{a}+2\iff \frac{b}{2a}=-2\iff b=-4a$ hay $\frac{b}{a}=-4$(1)

+) Tiếp tuyến  tại A có hệ số góc $k=\frac{-1}{2}\Rightarrow y\text{'}\left(\frac{-b}{a}\right)=\frac{-1}{2}$

$\begin{array}{l}\Rightarrow \frac{-2a-b}{{(\frac{-b}{a}-2)}^2}=\frac{-1}{2}\iff 2(-2a-b)=-{\left(\frac{-b}{a}-2\right)}^2\\ \iff -4a-2b=-\left(\frac{b^2}{a^2}+\text{}4\frac{b}{a}+\text{}4\right);\left(2\right)\end{array}$

Giải hệ phương trình (1)  và (2)  ta được:  a=  -1, b = 4

II. PHẦN TỰ LUẬN (5 điểm)

Câu 1:

a) $\underset{x\to 1}{\lim }\frac{3{\text{x}}^2-2\text{x}-1}{x^3-1}=\underset{x\to 1}{\lim }\frac{(x-1)(3x+1)}{(x-1)(x^2+x+1)}$ $=\underset{x\to 1}{\lim }\frac{3x+1}{x^2+x+1}=\frac{4}{3}$

b) Ta có: $\left\{\begin{array}{l}\underset{x\to 3^{-}}{\lim }(x-3)=0\\ x\to 3^{-}\iff x-3<0\\ \underset{x\to 3^{-}}{\lim }(x+3)=6>0\end{array}\right.$

Do đó, $\underset{x\to 3^{-}}{\lim }\frac{x+3}{x-3}=-\infty$

c) Ta có: 

$$\begin{gathered} \underset{x\to 1}{\lim }\frac{x-\sqrt{2x-1}}{x^2-12x+11}=\underset{x\to 1}{\lim }\frac{(x-\sqrt{2x-1})\left(x+\sqrt{2x-1}\right)}{(x-1)(x-11)\left(x+\sqrt{2x-1}\right)} \\ =\underset{x\to 1}{\lim }\frac{x^2-2x+1}{(x-1)(x-11)\left(x+\sqrt{2x-1}\right)}=\underset{x\to 1}{\lim }\frac{(x-1)}{(x-11)\left(x+\sqrt{2x-1}\right)}=0 \end{gathered}$$

Câu 2:

$f\left(x\right)=\left\{\begin{array}{l}\frac{2{\text{x}}^2-3\text{x}-2}{2\text{x}-4}khix\ne 2\\ \frac{3}{2}khix=2\end{array}\right.$

Tập xác định D = R.

Ta có: $f\left(2\right)=\frac{3}{2}$

$\underset{x\to 2}{\lim }f\left(x\right)=\underset{x\to 2}{\lim }\frac{2x^2-3x-2}{2x-4}=\underset{x\to 2}{\lim }\frac{(x-2)(2x+1)}{2(x-2)}=\underset{x\to 2}{\lim }\frac{2x+1}{2}=\frac{5}{2}$

Vì $\underset{x\to 2}{\lim }f\left(x\right)\ne f\left(2\right)$ nên hàm số không liên tục tại x = 2.

Câu 3.

a) Ta có $y=f\left(x\right)=-x^3-3{\text{x}}^2+9\text{x}+2011$

$f{}^{\text{'}}\left(x\right)=-3{\text{x}}^2-6\text{x}+9$

Để $f{}^{\text{'}}\left(x\right)\le 0\iff -3x^2-6x+9\le 0$

$\iff \left[\begin{array}{l}x\le -3\\ x\ge 1\end{array}\right.$

b) Với x₀ = 1 thì y₀= 2016 và f’(1) = 0

Do đó, phương trình tiếp tuyến tại điểm có hoành độ x= 1 là
y = 0(x- 1) + 2016  hay y = 2016.

Câu 4.

 

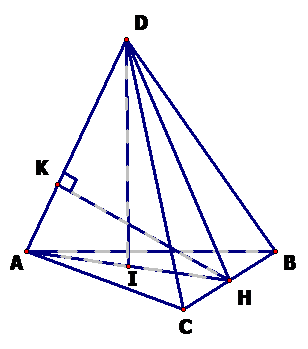
1) CMR: $BC\perp \left(ADH\right)$ và DH = a

ABC đều, H là trung điểm BC nên AH$\perp$BC, AD $\perp$BC

$\Rightarrow$ BC$\perp$(ADH) $\Rightarrow$BC$\perp$DH

$\Rightarrow$DH = d(D, BC) = a

2) CMR: DI$\perp$(ABC).

AD = a, DH = a, $△$DAH cân tại D.

 Mặt khác I là trung điểm  của AH nên DI $\perp$AH

BC$\perp$(ADH)$\Rightarrow$BC $\perp$DI

$\Rightarrow$DI $\perp$(ABC)

3) Tính khoảng cách giữa AD và BC

Trong $△$ADH vẽ đường cao HK tức là HK$\perp$AD (1)

Mặt khác BC$\perp$(ADH) nên BC$\perp$HK                 (2)

Từ (1) và (2) ta suy ra d(AD, BC) = HK

Xét $△$DIA vuông tại I ta có:

$DI=\sqrt{A{D}^2-A{I}^2}=\sqrt{a^2-{\left(\frac{a\sqrt{3}}{2}\right)}^2}=\sqrt{\frac{a^2}{4}}=\frac{a}{2}$

Xét $△$DAH ta có:

S=$\frac{1}{2}AH.DI$=$\frac{1}{2}AD.HK$

$\Rightarrow$ $d(AD,BC)=HK=\frac{AH.DI}{AD}=\frac{\frac{a\sqrt{3}}{2}.\frac{a}{2}}{a}=\frac{a\sqrt{3}}{4}$

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng học kì 2

Năm học 2022 - 2023

Môn: Toán 11

Thời gian làm bài: 45 phút

Đề thi Toán lớp 11 học kì 2 năm 2022 - 2023 có đáp án Đề số 2

Câu 1. Cho hàm số f(x)liên tục trên đoạn $\left[a; b\right]$ và $f\left(a\right)=b, f\left(b\right)=a$ với 0<a< b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).

A. f(x) + x² =0.

B. f(x) + a= 0.

C. f(x) – x = 0

D. f(x) + x =0.

Câu 2. Kết quả $L=\lim \left(5n-7n^5\right)$ là

A. $+\infty$

B. $-\infty$

C. 5

D. -7

Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc $\widehat{ABC}=60°$. Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

A. 60^o

B. 30^o

C. 45^o

D. 90^o

Câu 4. Một cấp số cộng gồm 8 số hạng với số hạng đầu bằng - 15 và số hạng cuối là 69. Tìm công sai của cấp số cộng.

A. -12

B. 10

C. 12

D. 10,5

Câu 5. Cho hình chóp S.ABCD có $SA\perp \left(ABC\right)$ và tam giác ABC vuông ở B. Gọi AH là đường cao của tam giác SAB. Khẳng định nào sau đây sai?

A. $SA\perp BC$

B. $AH\perp AC$

C. $AH\perp \text{S}C$

D. $AH\perp BC$

Câu 6. Tìm khẳng định đúng trong các khẳng định sau:

A. $\underset{x\to 0}{\lim }\frac{2x+3}{x^2-x+1}=0$

B. $\underset{x\to +\infty }{\lim }\frac{x^2+1}{2x^2-x+1}=\frac{1}{2}$

C. $\underset{x\to -\infty }{\lim }\frac{x^2+1}{2x^2-x+1}=-\frac{1}{2}$

D. $\underset{x\to 0}{\lim }\frac{1+x+x^2}{-x+1}=-1$

Câu 7. Biết $\underset{x\to -1}{\lim }\frac{x^2+ax+b}{x^2+x}=6$. Tìm tích của a.b.

A. ab = 20

B. ab = 15

C. ab = 10

D. ab= 5

Câu 8. Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2-x-2}{x-2};x\ne 2\\ m;x=2\end{array}\right.$. Với giá trị nào của tham số m thì hàm số đã cho liên tục tại điểm x m= 2?

A. m = 3

B. m = -3

C. m = -1

D. m = 1

Câu 9. Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P là trung điểm của các cạnh AD, DC, A’D’. Tính khoảng cách giữa CC’ và mặt phẳng (MNP) ?

A. $\frac{a\sqrt{2}}{4}$

B. $\frac{a\sqrt{3}}{3}$

C. $a\sqrt{2}$

D. $\frac{a}{\sqrt{2}}$

Câu 10. Một người muốn thuê khoan một giếng sâu 20m lấy nước tưới cho vườn cây của gia đình. Tìm hiểu tiền công khoan giếng ở một cơ sở nọ, họ tính theo cách sau đây: giá của mét khoan đầu tiên là 10.000 đồng và kể từ mét khoan thứ hai trở đi, giá của mỗi mét sau tăng lên 7% giá của mét khoan ngay trước nó. Hỏi người ấy cần phải trả số tiền bao nhiêu cho cơ sở khoan giếng?

A. 373790 đồng.

B. 455950 đồng.

C. 409955 đồng.

D. 448652 đồng.

Câu 11.Cho hình chóp S.ABCD có $SA\perp \left(ABCD\right)$, tứ giác ABCD là hình thang cân có đáy lớn AD gấp đôi đáy nhỏ BC và cạnh bên AB = BC. Mặt phẳng (P) đi qua A, vuông góc với SD và cắt SB, SC, SD lần lượt tại M, N, P. Khi đó ta có thể kết luận gì về tứ giác AMNP?

A. AMNP là một tứ giác nội tiếp (không có cặp cạnh đối nào song song).

B. AMNP là một hình thang vuông.

C. AMNP là một hình thang.             

D. AMNP là một hình chữ nhật.

Câu 12. Cho cấp số cộng (u_n) có tổng của n số hạng đầu tiên được tính bởi công thức S_n =  4n – n². Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:

A. M = -1

B. M= 1

C. M= 4

D. M=7

Câu 13. Trong các giới hạn sau, giới hạn nào không tồn tại.

A. $\underset{x\to 0}{\lim }\frac{\sqrt{3x^4}}{5x}$

B. $\underset{x\to -2}{\lim }\frac{x\left|x+2\right|}{x^2+3x+2}$

C. $\underset{x\to +\infty }{\lim }\frac{2x^2-10}{9-3x^3}$

D. $\underset{x\to -2}{\lim }\frac{x^3+8}{x+2}$

Câu 14. Gọi S là tập các số nguyên của a sao cho $\lim \left(\sqrt{4n^2+2017n-2018}-an\right)$ có giá trị hữu hạn. Tính tổng các phần tử của S.

A. S =  4

B. S= 0

C. S= 2

D. S=1

Câu 15. Cho hàm số $y=\left\{\begin{array}{ccc}-2x-1& khi& x<-1\\ 1+2x-x^2& khi& -1\le x\le 2\\ 1& khi& x>2\end{array}\right.$. Tìm khẳng định sai trong các khẳng định sau

A. Hàm số liên tục trên khoảng $\left(-\infty ;-1\right)$

B. Hàm số liên tục trên khoảng $\left(-1;+\infty \right)$

C. Hàm số liên tục tại điểm x_o = 2.      

D. Hàm số liên tục tại điểm x_o = -1.

Câu 16. Cho chuyển động thẳng xác định bởi phương trình s= t³ – 3t² – 9t + 2  ( t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng?

A. Vận tốc của chuyển động tại thời điểm t = 4 là v = 15 m/ s

B. Vận tốc của chuyển động tại thời điểm t = 5 là v= 18 m/ s

C. Vận tốc của chuyển động tại thời điểm t = 3 là v = 12 m/s.

D. Vận tốc của chuyển động bằng 0 khi t = 0 hoặc t = 2.

Câu 17. Cho dãy số (u_n) có $u_n=\frac{2n+5}{n^2+1}$. Số hạng bằng $\frac{1}{5}$ là số hạng thứ mấy?

A. 10

B. 6

C. 12

D. 11

Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $SA\perp \left(ABCD\right),SA=x.$ Tìm x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 60^o

A. x = 2a

B. x = $\frac{3a}{2}$

C. x = $\frac{a}{2}$

D. x = a

Câu 19.Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm x_o?

A. $\underset{x\to 0}{\lim }\frac{f\left(x+\Delta x\right)-f\left(x_0\right)}{\Delta x}$

B. $\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

C. $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

D. $\underset{x\to 0}{\lim }\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}$

Câu 21. Cho cấp số cộng (u_n) có số hạng đầu là u₁= 1 và công sai d= 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.

A. n = 79

B. n = 78

C. n= 77

D. n = 80

Câu 22. Tìm khẳng định đúng trong các khẳng định sau đây.

A. Hàm số có giới hạn tại điểm x = a thì có đạo hàm tại điểm x = a.

B. Hàm số có đạo hàm tại điểm x = a thì liên tục tại điểm x = a.       

C. Hàm số có giới hạn trái tại điểm x = a thì có đạo hàm tại điểm x = a.

D. Hàm số có liên tục tại điểm x = a thì có đạo hàm tại điểm x = a.

Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:

Hệ thống kiến thức Toán lớp 11 Giữa học kì 2

TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án

Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất

Bài tập Toán lớp 11 Học kì 2 có đáp án

Các dạng bài tập Toán lớp 11 Học kì 2