Hệ thống kiến thức Toán lớp 11 Giữa học kì 2
Hệ thống kiến thức Toán lớp 11 Giữa học kì 2 chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 11 Giữa học kì 2. Mời các bạn cùng đón xem:
Hệ thống kiến thức Toán lớp 11 Giữa học kì 2
Đề thi Toán lớp 11 Giữa học kì 2 năm 2022 - 2023 có đáp án
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi Toán lớp 11 Giữa học kì 2 năm 2022 - 2023 có đáp án Đề số 1
I. Trắc nghiệm (7,5 điểm )
Câu 1. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A.
B.
C.
D.
Lời giải
Dựa vào một số giới hạn đặc biệt ta có:
; ta có khẳng định D là đúng.
Chọn D.
Câu 2. Cho dãy số (un) xác định bởi . Tính lim un
A. 0
B.
C.
D.
Lời giải
Theo công thức giới hạn đặc biệt, ta có:
Mà nên lim un=0
Chọn A
Câu 3. Giá trị của bằng:
A.
B.
C.
D. 1
Lời giải
Chia cả tử và mẫu cho n2 - mũ cao nhất của phân thức ta được:
Chọn C.
Câu 4. Giá trị của bằng:
A.
B.
C. 16
D. 1
Lời giải
Ta có:
Suy ra
Chọn C.
Câu 5. Tính
A. 0
B.
C.
D. 2
Lời giải
Chọn A.
Câu 6. Viết số thập phân … (chu kỳ 03) dưới dạng số hữu tỉ
A.
B.
C.
D.
Lời giải
Trong đó lập thành cấp số nhân lùi vô hạn với số hạn đầu
Chọn B
Câu 7. Cho cấp số nhân lùi vô hạn, biết tổng S= 6 và tổng hai số hạng đầu . Tìm công bội của cấp số nhân đó?
A.
B.
C.
D. Đáp án khác
Lời giải
Theo đầu bài ta có:
Thay (1) vào (2) ta được:
Câu 8. Giá trị của bằng:
A.
B.
C.
D. 1
Lời giải
Ta có:
Chọn C
Câu 9. Tính giới hạn:
A. 0
B.
C.
D. 1
Lời giải
Ta có: 1+ 3+ 5 + ... + (2n +1) là tổng n số hạng của 1 cấp số cộng với số hạng đầu u1 =1 và công sai d= 2
Do đó, S = 1+ 3+ 5+ ...+(2n+ 1)
Suy ra
Chọn B
Câu 10. Giá trị của bằng:
A.
B.
C.
D. 1
Lời giải
Ta có:
Câu 11. bằng:
A.
B. 1
C. 0
D.
Lời giải
Ta có:
Nhưng ,
và
Nên
Chọn A
Câu 12. Tính
A. - 2
B.
C.
D. 2
Lời giải
![]()
Chọn A
Câu 13. Tìm a để hàm số có giới hạn tại
A.
B.
C.
D. 1
Lời giải
Ta có:
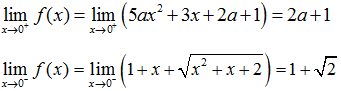
Vậy để hàm số có giới hạn khi
Chọn C.
Câu 14. Tính
A.
B. 0
C.
D.
Lời giải
![]()
Chọn B
Câu 15. Tìm giới hạn:
A.
B.
C.
D. 0
Lời giải
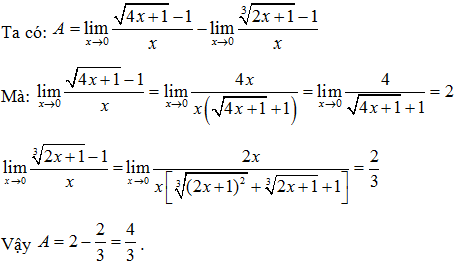
Chọn C.
Câu 16. Giá trị đúng của
A. -1
B. 1
C. 7
D.
Lời giải
Chia cả tử và mẫu của phân thức cho x4 lũy thừa bậc cao nhất của x ta được:
Chọn B.
Câu 17. Tìm giới hạn
A.
B.
C.
D. 0
Lời giải
Ta có:
Chọn B
Câu 18. Chọn kết quả đúng trong các kết quả sau của là:
A.
B. 0
C. 4
D.
Lời giải
Vì
Chọn A.
Câu 19. bằng:
A.
B. - 1
C. 1
D.
Lời giải
= vì
Chọn D
Câu 20. Tìm giới hạn
A.
B.
C. 1
D. 0
Ta có 1- cos2x = 2sin2x nên:
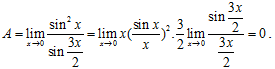
Chọn D.
Câu 21. Cho hàm số Tìm k để f(x) gián đoạn tại x= 1.
A.
B.
C.
D.
Lời giải
TXĐ: D = R.
Với x= 1 ta có f(1) = k2
Với x ≠ 1 ta có
Vậy để hàm số gián đoạn tại x = 1 khi
Chọn A
Câu 22. Tìm m để hàm số liên tục tại x= 2.
A. m = 1
B. m = 2
C. m = - 1
D. m = - 2
Lời giải
Hàm đã cho xác định trên R.
Ta có: và
Để hàm số liên tục tại x=2 thì
Chọn B.
Câu 23. Tính biết khi
A.
B.
C.
D. Không tồn tại
Lời giải
Ta có:
Vậy
Chọn A.
Câu 24. Cho hình lăng trụ . M là trung điểm của BB'. Đặt , , . Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Hướng dẫn giải:
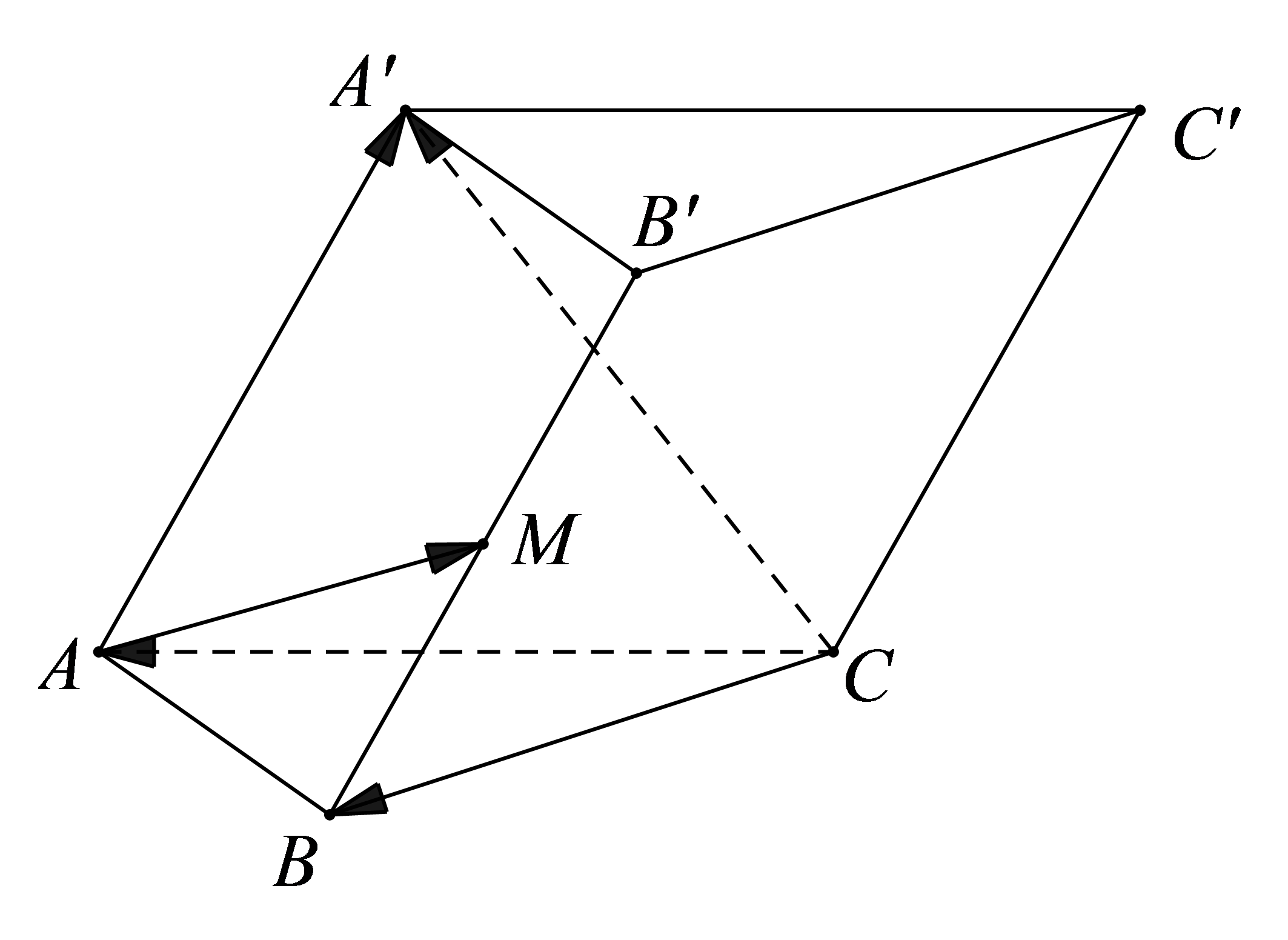
Ta phân tích như sau:
Chọn D.
Câu 25. Cho hình lập phương có cạnh bằng a. Ta có bằng?
A.
B.
C.
D.
Hướng dẫn giải:
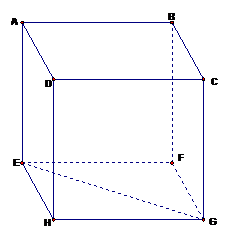
(Vì
Chọn B.
Câu 26. Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M, N sao cho AM = 3MD, BN = 3NC. Gọi P, Q lần lượt là trung điểm của AD và BC. Trong các khẳng định sau, khẳng định nào sai?
A. Các vectơ đồng phẳng
B. Các vectơ đồng phẳng
C. Các vectơ đồng phẳng
D. Các vectơ đồng phẳng
Lời giải
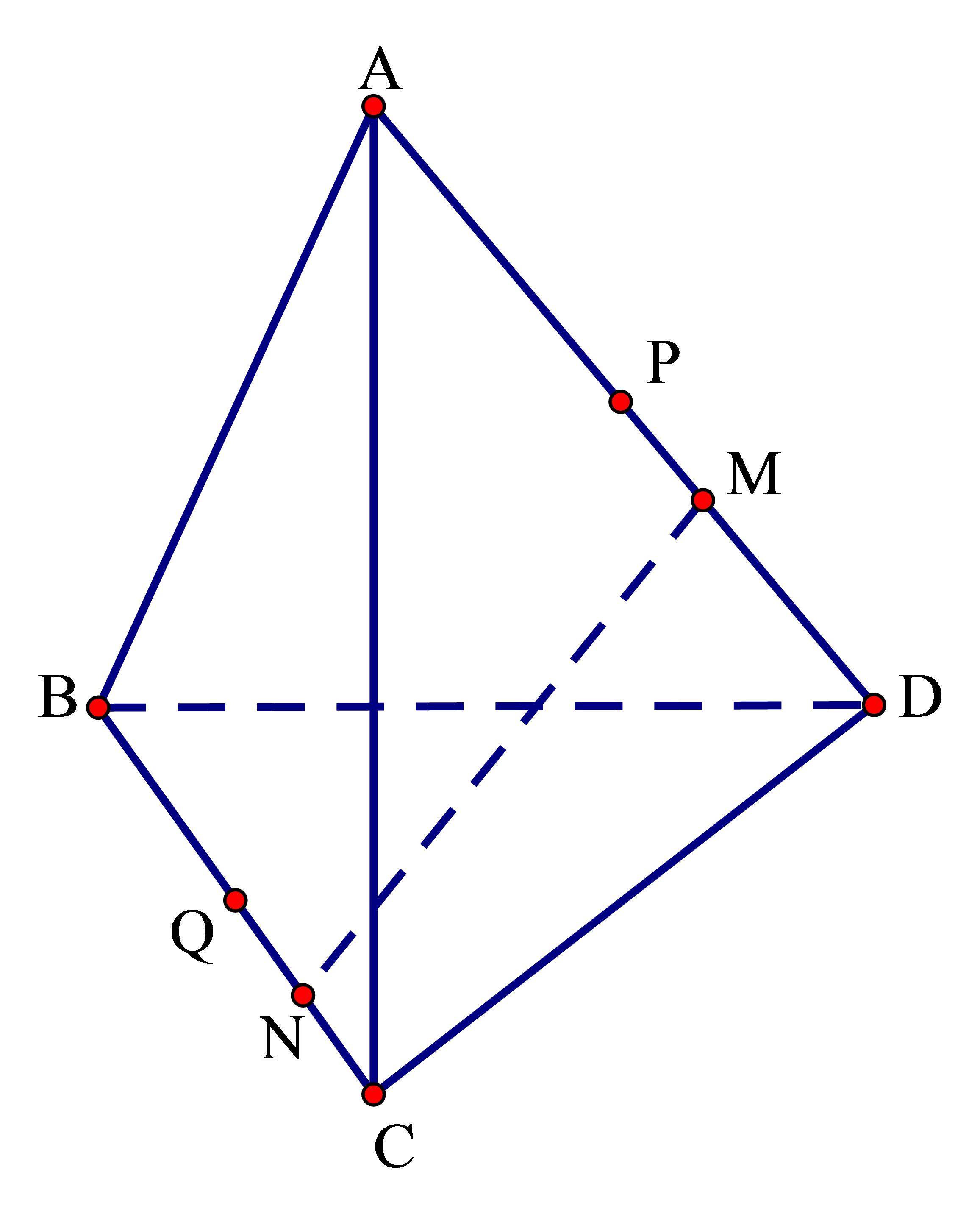
A. Sai vì
không đồng phẳng.
B. Đúng vì đồng phẳng.
C. Đúng. Bằng cách biểu diễn tương tự như trên ta có
D. Đúng. Biểu diễn giống đáp án A ta có .
Chọn A.
Câu 27. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc bằng
A. 30o
B. 45o
C. 60o
D. 90o
Hướng dẫn giải:
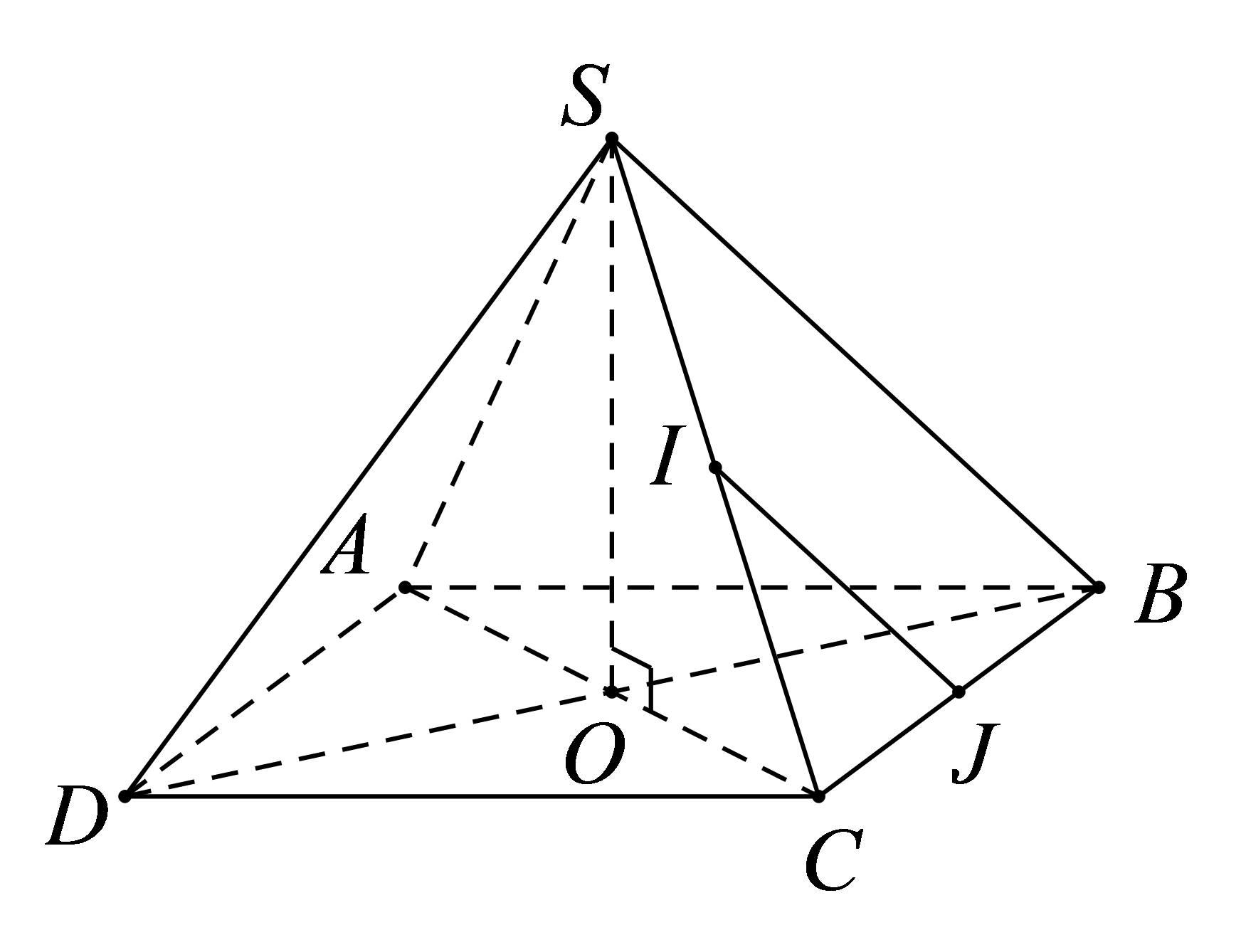
Gọi O là tâm của hình vuông ABCD
=> O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1).
Ta có: SA = SB = SC = SD = a nên S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2)
Từ giả thiết ta có: (do IJ là đường trung bình của ).
Mặt khác, ta lại có đều, do đó:
Chọn C.
Câu 28. Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc giữa bằng:
A. 30o
B. 45o
C. 60o
D. 90o
Hướng dẫn giải
Xét tam giác ABC có IJ là đường trung bình nên: (1)
Xét tam giác ABD có EF là đường trung bình của tam giác nên: (2)
Từ (1); (2) suy ra: IJ // EF và IJ = EF
Từ đó suy ra tứ giác IJEF là hình bình hành.
Mặt khác: là hình thoi (tính chất hai đường chéo của hình thoi)
Chọn D.
Câu 29. Cho hình chóp S.ABC có và . Hãy xác định góc giữa cặp vectơ và ?
A. 60o
B. 120o
C. 45o
D. 90o
Hướng dẫn giải:
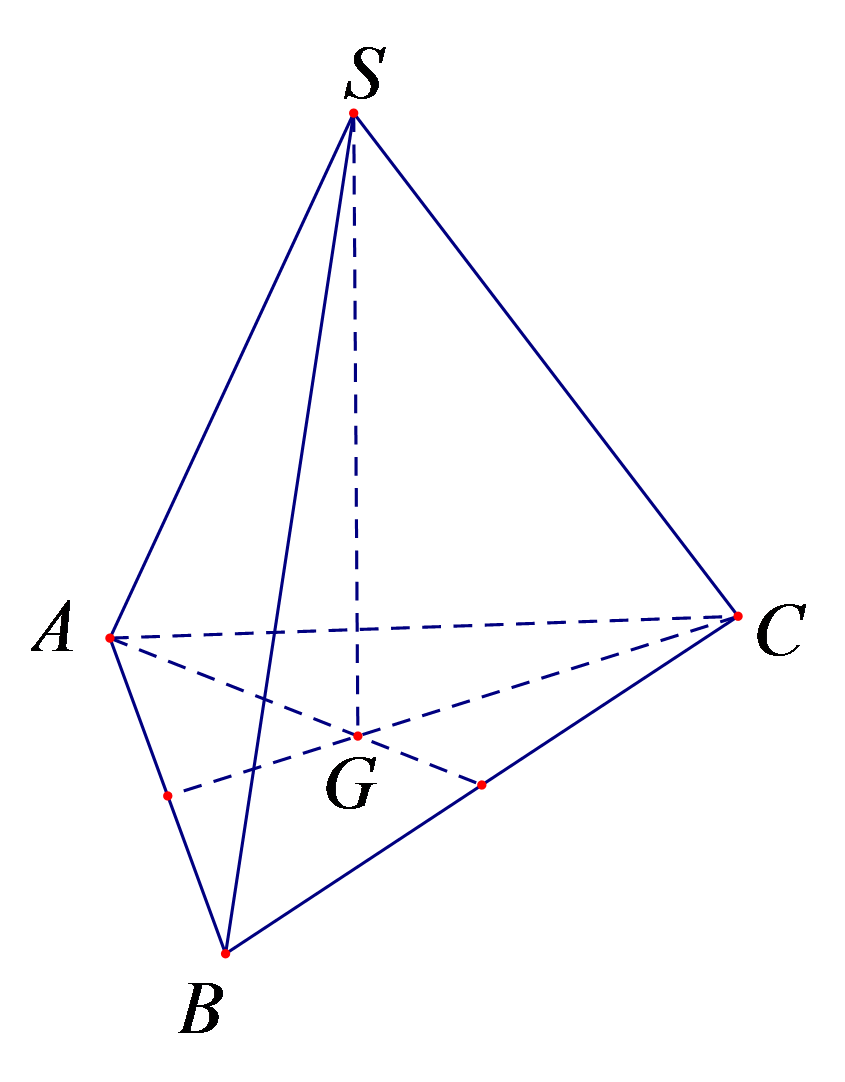
Ta có: .
Do đó, tam giác ABC đều.
Gọi G là trọng tâm của tam giác ABC.
Vì hình chóp S.ABC có SA= SB = SC nên hình chiếu của S lên mp(ABC) trùng với G.
Hay
Ta có:
Suy ra .
Vậy góc giữa cặp vectơ và bằng 90o.
Chọn D.
Câu 30. Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?
A. 120o
B. 60o
C. 90o
D. 30o
Hướng dẫn giải
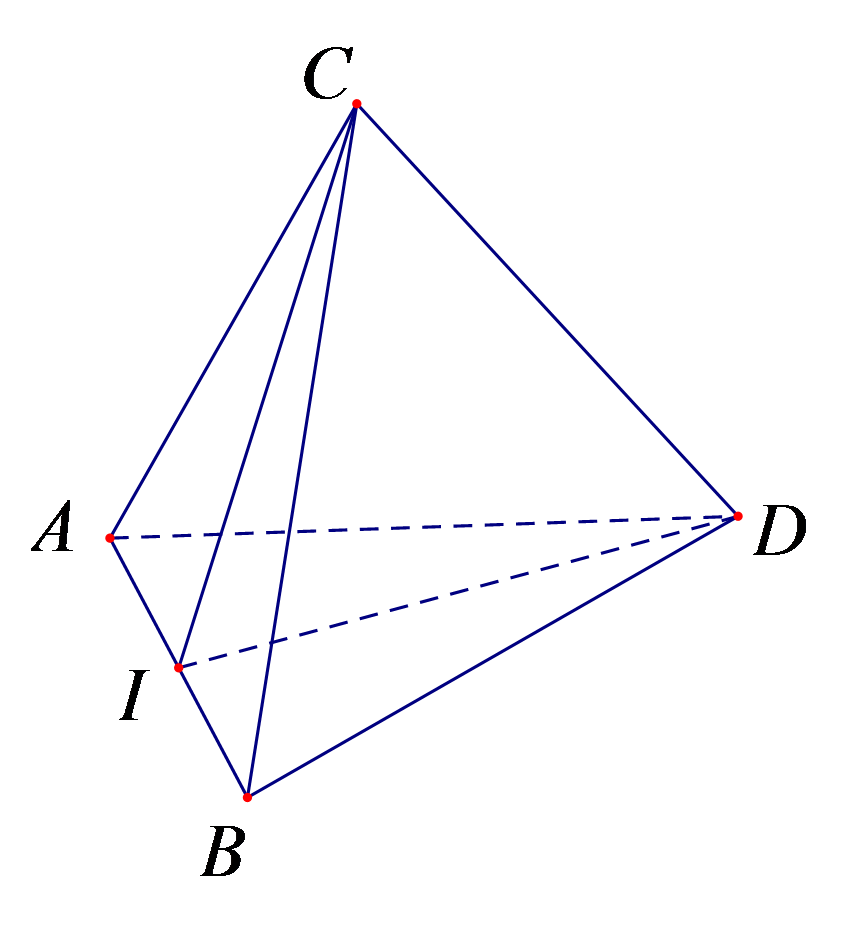
Gọi I là trung điểm của AB
Vì ABC và ABD là các tam giác đều
Nên
Suy ra
Do đó, góc giữa AB và CD là 90o
Chọn C.
II. Tự luận ( 2,5 điểm)
Bài 1( 0,5 điểm). Tính giới hạn:
Lời giải
Đặt
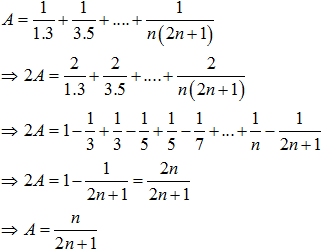
Nên
Bài 2 (1,5 điểm). Cho hàm số:
a) Tìm a để liên tục tại trái điểm x = 1
b) Tìm a để liên tục tại phải điểm x = 1
c) Tìm a để liên tục trên R
Lời giải
Ta có:
a) Để liên tục trái tại điểm x = 1
và
Vậy điều kiện là a = -1
b) Để liên tục phải tại điểm x = -1
tồn tại và
Ta có: và
Vậy điều kiện là
c) Hàm số liên tục trên R trước hết hàm số liên tục tại x=1
(mâu thuẫn)
Vậy không tồn tại a để hàm số liên tục trên R.
Bài 3 (0,5 điểm). Chứng minh rằng phương trình có nghiệm duy nhất x0 thỏa mãn
Lời giải
Xét hàm số , ta có và nên
Mặt khác: là hàm đa thức nên liên tục trên với mọi thuộc R.
Suy ra đồng biến trên R nên phương trình có nghiệm duy nhất .
Theo bất đẳng thức Côsi:
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi Toán lớp 11 Giữa học kì 2 năm 2022 - 2023 có đáp án Đề số 2
I. Trắc nghiệm
Câu 1. bằng
A. 0
B. 1
C.
D.
Lời giải
Ta có:
Vì và nên
Chọn D.
Câu 2. Tính lim un với
A. 0
B. 5
C. 3
D. -7
Lời giải
Ta có: .
Chọn B
Câu 3. Giới hạn của dãy số (un) với bằng
A. 1
B. 0
C.
D.
Lời giải
Chia cả tử và mẫu của phân thức cho n4 ( n4 là bậc cao nhất của n trong phân thức), ta được
()
Chọn B
Câu 4. bằng
A. 0
B. 1
C.
D. 2
Lời giải
Ta có mà nên
Chọn A.
Câu 5. bằng:
A. -1
B. 3
C.
D.
Lời giải
Ta có
Vì và nên
Chọn C
Câu 6. bằng
A.
B. 3
C.
D.
Lời giải
Ta có
Vì và nên
Chọn C
Câu 7. bằng :
A. 0
B.
C. 36
D.
Lời giải
Chọn A
Câu 8. Cho số thập phân vô hạn tuần hoàn (chu kỳ 15), a được biểu diễn dưới dạng phân số tối giản trong đó m, n là các số nguyên dương. Tìm tổng m+ n.
A. 104
B. 312
C. 86
D. 78
Lời giải
Ta có
Vì là tổng của cấp số nhân lùi vô hạn với số hạng đầu ,công bội nên
Vậy m = 71, n= 33 nên m + n = 104.
Chọn A
Câu 9. bằng:
A. -2
B. 3
C.
D.
Lời giải
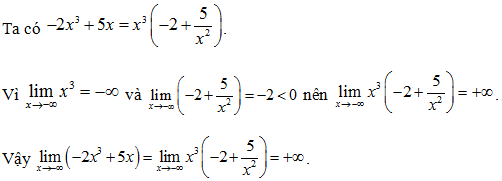
Chọn C.
Câu 10. bằng:
A.
B.
C.
D. 0
Lời giải
Vì
(Vì )
Do đó = 0
Chọn D
Câu 11. Giới hạn bên phải của hàm số khi là
A.
B.
C. 3
D.
Lời giải
Hàm số xác định trên R\{2}.
Ta có với mọi x > 2 và
Do đó
Chọn B
Câu 12. Cho hàm số f(x) có đồ thị như hình dưới đây:
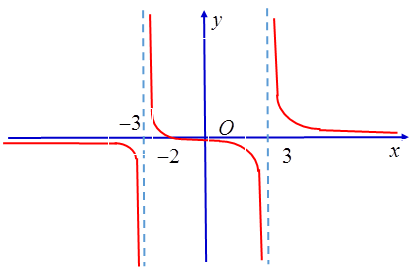
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là ?
A.
B.
C.
D.
Lời giải
Khi , đồ thị hàm số là một đường cong đi lên từ phải qua trái.
Do đó
Tương tự như vậy ta có = = 0;
Chọn C.
Câu 13. Tính
A. 1
B. 4
C. -2
D. -4
Lời giải
Ta có
Chọn B.
Câu 14. Giới hạn của hàm số bằng
A.
B.
C.
D.
Lời giải
Chọn A.
Câu 15. Giả sử = L. Hệ số a bằng bao nhiêu để L = 3 ?
A. -6
B. 6
C. -12
D. 12
Lời giải
Ta có
Vậy L =
Do đó để L = 3
Chọn D.
Câu 16. Cho a và b là các số thực khác 0. Khi đó bằng?
A. a
B. b
C.
D.
Lời giải
Ta có
.
Chọn C.
Câu 17. Giới hạn bằng :
A.
B.
C.
D.
Lời giải
Ta đưa x2 ra ngoài căn rồi chia cả tử và mẫu cho x. Cụ thể như sau:
Chọn B
Câu 18. Giới hạn bằng :
A. 0
B. -1
C. 1
D.
Lời giải
Ta có :
Chọn B
Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:
TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án
Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất
Bài tập Toán lớp 11 Học kì 2 có đáp án
