Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất
Đề cương Học kì 2 Toán lớp 11 chi tiết nhất giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 11 học kì 2. Mời các bạn cùng đón xem:
Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất
A. NỘI DUNG ÔN TẬP
I. ĐẠI SỐ VÀ GIẢI TÍCH
1. DÃY SỐ – CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN:
+ Phương pháp chứng minh quy nạp.
+ Xác định một dãy số: Tìm các số hạng của một dãy số cho trước, tìm các số hạng của cấp số nhân, cấp số cộng.
+ Xét tính tăng giảm và tính bị chặn của một dãy số.
+ Xét một dãy số có là một cấp số cộng hoặc cấp số nhân hay không. Xét xem một số cho trước có là một số hạng của cấp số cộng hoặc cấp số nhân không.
+ Tìm các số hạng đầu và công sai của cấp số cộng, tìm số hạng đầu và công bội của cấp số nhân.
+ Giải các bài toán sử dụng tính chất của cấp số cộng và cấp số nhân.
+ Giải các bài toán thực tế áp dụng của cấp số cộng, cấp số nhân.
2. GIỚI HẠN – HÀM SỐ LIÊN TỤC:
+ Tìm giới hạn của dãy số.
+ Tìm giới hạn của hàm số.
+ Giải quyết các bài toán áp dụng giới hạn.
+ Xét tính liên tục của hàm số tại một điểm, xét tính liên tục của hàm số trên một khoảng.
+ Tìm điều kiện để hàm số liên tục tại một điểm hoặc liên tục trên một khoảng.
+ Áp dụng định lý về hàm số liên tục để xét số nghiệm của phương trình.
+ Các bài toán áp dụng.
3. ĐẠO HÀM:
+ Tìm đạo hàm tại một điểm của hàm số.
+ Tìm đạo hàm trên một khoảng của hàm số.
+ Tìm điều kiện để hàm số có đạo hàm.
+ Tìm đạo hàm cấp cao của một hàm số.
+ Bài toán tiếp tuyến của đạo hàm.
+ Bài toán ứng dụng thực tế của đạo hàm.
+ Một số bài toán khác về đạo hàm của hàm số.
II. HÌNH HỌC
4. VÉC TƠ TRONG KHÔNG GIAN – QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
+ Các bài toán về véc tơ trong không gian.
+ Chứng minh hai đường thẳng vuông góc.
+ Chứng minh đường thẳng vuông góc với mặt phẳng.
+ Chứng minh hai mặt phẳng vuông góc.
+ Bài toán về góc: Góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng; góc giữa hai mặt phẳng.
+ Bài toán về khoảng cách: Khoảng cách từ một điểm đến 1 đường thẳng; khoảng cách từ một điểm đến một mặt phẳng; khoảng cách từ một đường thẳng đến một mặt phẳng; khoảng cách giữa hai mặt phẳng; khoảng cách giữa hai đường thẳng chéo nhau.
+ Bài toán về giao điểm của một đường thẳng và một mặt phẳng; bài toán về giao tuyến của hai mặt phẳng; bài toán về thiết diện.
+ Một số bài toán áp dụng quan hệ vuông góc trong không gian.
B. BÀI TẬP














Xem thêm:
Đề thi học kì 2 Toán lớp 11 năm 2022 - 2023 có ma trận
Ma trận đề
|
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ nhận thức |
Tổng |
% tổng điểm
|
|
|||||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
|||||||||||
|
Số CH |
Thời gian
|
|
||||||||||||
|
Số CH |
Thời gian
|
Số CH |
Thời gian
|
Số CH |
Thời gian
|
Số CH |
Thời gian
|
TN |
TL |
|
||||
|
Giới hạn |
Giới hạn của dãy số |
5 |
5 |
2 |
4 |
1 |
8 |
1 |
12 |
23 |
3 |
63 |
66 |
|
|
Giới hạn của hàm số |
||||||||||||||
|
Hàm số liên tục |
||||||||||||||
|
Đạo hàm |
Định nghĩa và ý nghĩa của đạo hàm |
1 |
1 |
1 |
2 |
1 |
12 |
|
||||||
|
Quy tắc tính đạo hàm |
6 |
6 |
2 |
4 |
|
|
|
|||||||
|
Đạo hàm của hàm số lượng giác |
3 |
3 |
3 |
6 |
|
|
|
|||||||
|
Đạo hàm cấp hai |
|
|
2 |
4 |
|
|
|
|
2 |
|
4 |
4 |
|
|
|
Vectơ trong không gian. Quan hệ vuông góc trong không gian. |
Vectơ trong không gian |
1 |
1 |
|
|
1 |
8 |
|
|
10 |
1 |
23 |
30 |
|
|
Hai đường thẳng vuông góc |
1 |
1 |
1 |
2 |
|
|
||||||||
|
Đường thẳng vuông góc với mặt phẳng |
1 |
1 |
2 |
4 |
|
|
||||||||
|
Hai mặt phẳng vuông góc |
1 |
1 |
1 |
2 |
|
|
||||||||
|
Khoảng cách |
1 |
1 |
1 |
2 |
|
|
||||||||
|
Tổng |
20 |
|
15 |
|
2 |
|
2 |
|
35 |
4 |
90 |
100 |
||
|
Tỉ lệ (%) |
40 |
30 |
20 |
10 |
|
|
|
|
||||||
|
Tỉ lệ chung (%) |
70 |
30 |
|
|
|
|||||||||
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi học kì 2 Toán lớp 11 năm 2022 - 2023 có ma trận Đề số 1
I. Trắc nghiệm (6 điểm)
Câu 1: Hàm số nào sau đây không liên tục trên R?
A.
B.
C.
D.
Câu 2: Tính bằng
A. 1
B.
C. -1
D.
Câu 3: Tính bằng
A.
B.
C.
D.
Câu 4: Chứng minh rằng phương trình có ít nhất một nghiệm.
Một bạn học sinh trình bày lời giải như sau:
Bước 1: Xét hàm số liên tục trên
Bước 2: Ta có f(0) = 3và f(-2) = -3.
Bước 3: Suy ra f(0).f(-2) > 0.
Bước 4: Vậy phương trình đã cho có ít nhất 1 nghiệm.
Hãy tìm bước giải sai của bạn học sinh trên ?
A. Bước 1.
B. Bước 2.
C. Bước 3.
D. Bước 4 .
Câu 5: Đạo hàm của hàm số tại là
A.
B.
C.
D.
Câu 6: Khẳng định nào sau đây sai?
A.
B.
C.
D.
Câu 7: Cho . Hãy chọn khẳng định sai?
A.
B.
C.
D.
Câu 8: Tính đạo hàm của hàm số sau .
A.
B.
C.
D.
Câu 9: Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 10: Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 11: Đạo hàm cấp hai của hàm số là
A.
B.
C.
D.
Câu 12: Cho hình hộp ABCD.A’B’C’D’. Đẳng thức nào sau đây là sai?
A.
B.
C.
D.
Câu 13: Cho hình lập phương ABCD.A’B’C’D’. Tìm góc giữa hai vectơ và .
A. 45o
B. 30o
C. 60o
D. 120o
Câu 14: Trong không gian, phát biểu nào sau đây là sai ?
A. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
B. Nếu hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
C. Cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
D. Hai đường thẳng vuông góc với nhau thì chúng có thể cắt nhau hoặc chéo nhau.
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, và AH là đường cao của . Khẳng định nào sau đây sai ?
A.
B.
C.
D.
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và . Chọn khẳng định sai ?
A.
B.
C.
D.
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và . Khi đó, mặt phẳng (SDC) vuông góc với mặt phẳng
A. (SBC)
B. (SAC)
C. (SAD)
D. (ABCD)
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = x. Tìm x để góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60o là
A.
B.
C.
D.
Câu 19: Một vật được thả rơi tự do ở độ cao 147m có phương trình chuyển động , trong đó và t tính bằng giây (s). Tính vận tốc của vật tại thời điểm vật tiếp đất.
A. 30 m/s
B. m/s
C. m/s
D. m/s
Câu 20: Cho a và b là hai đường thẳng chéo nhau, biết và . Khẳng định nào sau đây là sai?
A. Khoảng cách giữa hai đường thẳng a và b bằng khoảng cách từ đường thẳng a đến mặt phẳng (Q).
B. Khoảng cách giữa hai đường thẳng a và b bằng khoảng cách từ một điểm A tùy ý thuộc đường thẳng a đến mặt phẳng (Q).
C. Khoảng cách giữa hai đường thẳng a và b không bằng khoảng cách giữa hai mặt phẳng (P) và (Q).
D. Khoảng cách giữa hai đường thẳng a và b bằng độ dài đoạn thẳng vuông góc chung của chúng.
II. Phần tự luận (4,0 điểm):
Bài 1( 0,5 điểm): Viết phương trình tiếp tuyến của đồ thị hàm số , biết tiếp tuyến song song với đường thẳng .
Bài 2 ( 1,5 điểm): Tính đạo hàm của các hàm số sau:
a)
b)
c)
Bài 3 ( 2,0 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, và . Gọi M , N lần lượt là trung điểm của BC và CD.
a) Chứng minh:
b) Tính góc giữa SM và (ABCD).
c) Tính khoảng cách từ điểm C đến mặt phẳng (SMN).
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi học kì 2 Toán lớp 11 năm 2022 - 2023 có ma trận Đề số 2
I. PHẦN TRẮC NGHIỆM (7 điểm)
Câu 1: Cho hai dãy và thỏa mãn và Giá trị của bằng
A. 5
B. 6
C. -1
D. 1
Câu 2:bằng
A. 0
B.
C. 1
D.
Câu 3: bằng
A. 0
B.
C. 1
D.
Câu 4: bằng
A. 3
B. -1
C. 1
D.
Câu 5: bằng
A.
B. 2
C. 3
D.
Câu 6: Cho hàm số có đồ thị (C) và đạo hàm Hệ số góc của tiếp tuyến của (C) tại điểm bằng
A. 6
B. 3
C. 2
D. 12
Câu 7: Đạo hàm của hàm số y = x2 tại điểm x = 3 bằng
A. 6
B. 12
C. 3
D. 9
Câu 8: Đạo hàm của hàm số y = x2 + x là
A. 2x + 1
B. 2x
C. 2x2 + 1
D. 2x2 + x
Câu 9: Đạo hàm của hàm số y = x3 – 2x là
A. 3x2 - 2
B. 3x2
C. 3x3 - 2
D. 2x2 - 2
Câu 10: Cho hai hàm số f(x) và g(x) có f’(1) = 2 và g’(1) = 3. Đạo hàm của hàm số f(x) + g(x) tại điểm x = 1 bằng
A. 5
B. 6
C. 1
D. -1
Câu 11: Cho hai hàm số f(x) và g(x) có f’(1) = 3 và g’(1) = 1. Đạo hàm của hàm số f(x) – g(x) tại điểm x = 1 bằng
A. 2
B. 3
C. 4
D. -2
Câu 12: Cho hàm số f(x) có đạo hàm f’(x) = 2x + 4 với mọi Hàm số 2f(x) có đạo hàm là
A. 4x + 8
B. 4x + 4
C. x + 2
D. 2x + 6
Câu 13: Đạo hàm của hàm số y = cosx là
A. –sin x
B. sin x
C. –cos x
D. cos x
Câu 14: bằng
A. 1
B. -1
C. 0
D.
Câu 15: Đạo hàm của hàm số y = x + sin x là
A. 1 + cos x
B. 1 – cos x
C. cos x
D. -cos x
Câu 16: Trong không gian, cho hình bình hành ABCD Vectơ bằng
A.
B.
C.
D.
Câu 17: Trong không gian, với là ba vectơ bất kỳ, mệnh đề nào dưới đây đúng ?
A.
B.
C.
D.
Câu 18: Trong không gian cho điểm A và mặt phẳng (P). Mệnh đề nào dưới đây đúng ?
A. Có đúng một đường thẳng đi qua A và vuông góc với (P).
B. Có đúng hai đường thẳng đi qua A và vuông góc với (P).
C. Có vô số đường thẳng đi qua A và vuông góc với (P).
D. Không tồn tại đường thẳng đi qua A và vuông góc với (P).
Câu 19: Hình lăng trụ đứng tam giác có bao nhiêu mặt là hình chữ nhật?
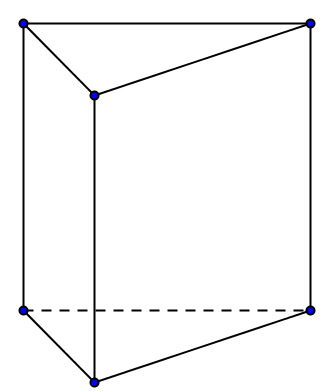
A. 3
B. 5
C. 1
D. 2
Câu 20: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ A' đến mặt phẳng (ABCD) bằng
A. 2a
B. a
C. 3a
D.
Câu 21: Cho (un) là cấp số nhân với u1= 3 và công bội Gọi Sn là tổng của n số hạng đầu tiên của cấp số nhân đã cho. Ta có lim Sn bằng
A. 6
B.
C. 3
D.
Câu 22: Giá trị thực của tham số m để hàm số liên tục tại x = 2 bằng
A. 5
B. 3
C. 2
D. 1
Câu 23: Tiếp tuyến của đồ thị hàm số tại điểm M(1; -1) có hệ số góc bằng
A. -1
B. 1
C. 7
D. 5
Câu 24: Đạo hàm của hàm số y = (2x + 1)2 là
A. y' = 8x + 4
B. y' = 2x + 1
C. y' = 4x + 2
D. y' = 4x + 1
Câu 25: Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 26: Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 27: Đạo hàm của hàm số y = xsin x là
A.
B.
C.
D.
Câu 28: Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 29: Đạo hàm cấp hai của hàm số là
A. 6x
B. 6x + 2
C. 3x
D. 3x + 2
Câu 30: Cho hàm số Giá trị của bằng
A. 12
B. 6
C. 24
D. 4
Câu 31: Trong không gian cho hai vectơ tạo với nhau một góc 60o, và Tích vô hướng bằng
A. 3
B. 6
C. 2
D.
Câu 32: Cho hình chóp S.ABCD có ABCD là hình chữ nhật và Mệnh đề nào dưới đây đúng ?
A.
B.
C.
D.
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = a. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng
A. 45o
B. 90o
C. 30o
D. 60o
Câu 34: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy. Mặt phẳng (ABCD) vuông góc với mặt phẳng nào dưới đây ?
A. (SAC)
B. (SBD)
C. (SCD)
D. (SBC)
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a và Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng
A. a
B. a
C. 2a
D. a
II. PHẦN TỰ LUẬN (3 điểm)
Câu 1: Cho hàm số với Hãy xác định các số a, b, c biết rằng và đồ thị của hàm số đi qua các điểm (-1; -3) và (1; -1).
Câu 2: Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60o. Tính độ dài đường cao của hình chóp đã cho.
Câu 3:
a) Giả sử hai hàm số và đều liên tục trên đoạn [0; 2] và Chứng minh phương trình luôn có nghiệm thuộc đoạn [0; 1].
b) Cho hàm số có đồ thị (C). Tìm điểm M thuộc (C) sao cho tiếp tuyến của (C) tại M tạo với hai trục tọa độ một tam giác vuông cân.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi học kì 2 Toán lớp 11 năm 2022 - 2023 có ma trận Đề số 3
I) TRẮC NGHIỆM: (7,0 điểm)
Câu 1: Cho hình hộp ABCD.A’B’C’D’ (hình vẽ minh hoạ).
Mệnh đề nào sau đây đúng ?
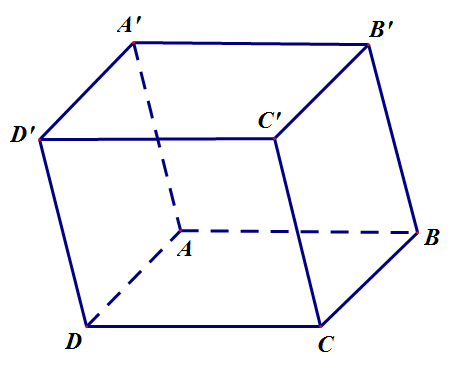
A.
B.
C.
D.
Câu 2: Tìm đạo hàm của hàm số với
A.
B.
C.
D.
Câu 3. Trong không gian, hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng
A. 0o
B. 45o
C. 90o
D. 60o
Câu 4. Cho hàm số có đạo hàm tại điểm x0. Chọn khẳng định ĐÚNG?
A.
B.
C.
D.
Câu 5: Tính ta được kết quả là
A. 3
B.
C. 0
D.
Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:
Hệ thống kiến thức Toán lớp 11 Giữa học kì 2
TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án
Bài tập Toán lớp 11 Học kì 2 có đáp án
