Các dạng bài tập Toán lớp 11 giữa học kì 2

Các dạng bài tập Toán lớp 11 Giữa học kì 2

A. ĐẠI SỐ VÀ GIẢI TÍCH

Các dạng bài tập Giới hạn

50 bài tập về Giới hạn của dãy số (có đáp án 2022) – Toán 11

50 bài tập về Giới hạn của hàm số (có đáp án 2022) – Toán 11

50 bài tập về Hàm số liên tục (có đáp án 2022) – Toán 11

Các dạng bài tập Đạo hàm

50 bài tập về Cách tính đạo hàm bằng định nghĩa hay (có đáp án 2022)– Toán 11

50 bài tập về Quy tắc tính đạo hàm (có đáp án 2022) – Toán 11

50 bài tập về Đạo hàm của hàm số lượng giác (có đáp án 2022) – Toán 11

50 bài tập về Ứng dụng Đạo hàm để giải phương trình, bất phương trình (có đáp án 2022) – Toán 11

50 bài tập về Các bài toán về vi phân, đạo hàm cấp cao và ý nghĩa của đạo hàm (có đáp án 2022) – Toán 11

50 bài tập về Các dạng bài tập về tiếp tuyến lớp 11 (có đáp án 2022) – Toán 11

B. HÌNH HỌC

Các dạng bài tập Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

50 bài tập về Đại cương về đường thẳng (có đáp án 2022) – Toán 11

50 bài tập về Hai đường thẳng song song trong không gian (có đáp án 2022) – Toán 11

50 bài tập về Đường thẳng và mặt phẳng song song (có đáp án 2022) – Toán 11

50 bài tập về Hai mặt phẳng song song (có đáp án 2022) – Toán 11

Công thức Giao tuyến của ba mặt phẳng và hệ quả

Công thức Chứng minh hai đường thẳng song song trong không gian

Công thức Chứng minh đường thẳng song song với mặt phẳng

Công thức Chứng minh hai mặt phẳng song song

50 bài tập về Định lý Ta-lét trong không gian đầy đủ (có đáp án 2022) - Toán 11

Giới hạn của dãy số và cách giải bài tập - Toán lớp 11

1. Lý thuyết

a) Dãy số có giới hạn 0

Ta nói rằng dãy số (u_n) có giới hạn là 0 khi n dần tới dương vô cực, nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số kể từ một số hạng nào đó trở đi, |u_n| nhỏ hơn số dương đó.

Kí hiệu: $\underset{n\to \infty }{\lim }{u}_n=0$ hay lim u_n = 0 hay $u_n\to 0$ khi $n\to +\infty$.

b) Dãy số có giới hạn hữu hạn

Ta nói rằng dãy số (u_n) có giới hạn là số thực L nếu lim (u_n – L) = 0

Kí hiệu: $\underset{n\to \infty }{\lim }{u}_n=L$ hay lim u_n = L hay $u_n\to L$ khi $n\to +\infty$.

c) Dãy số có giới hạn vô cực

Dãy số (u_n) có giới hạn là $+\infty$ khi $n\to +\infty$, nếu u_n có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

Ký hiệu: $\lim u_n=+\infty$ hoặc $u_n\to +\infty khin\to +\infty$

Dãy số (u_n) có giới hạn là $-\infty$ khi $n\to +\infty$, nếu $\lim \left(-u_n\right)=+\infty$

Ký hiệu: $\lim u_n=-\infty$ hoặc $u_n\to -\infty khin\to +\infty$

d) Một vài giới hạn đặc biệt

$\lim u_n=0\iff \lim \left|u_n\right|=0$

$\lim \frac{1}{n}=0; \lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right)$

$\lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right)$

$\lim q^n=\left\{\begin{array}{l}0khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.$

e) Định lý về giới hạn hữu hạn

* Nếu lim u_n = a và lim v_n = b và c là hằng số. Khi đó ta có :

lim(u_n + v_n) = a + b

lim(u_n - v_n) = a - b

lim(u_n v_n) = a.b

$\lim \frac{u_n}{v_n}=\frac{a}{b},\left(b\ne 0\right)$

lim(cu_n ) = c.a

lim|u_n | = |a|

$\lim \sqrt[3]{u_n}=\sqrt[3]{a}$

Nếu $u_n\ge 0$ với mọi n thì $a\ge 0$ và $\lim \sqrt{u_n}=\sqrt{a}$.

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n):

Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a.

Hệ quả: Cho hai dãy số (u_n) và (v_n):

Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

f) Một vài quy tắc tìm giới hạn vô cực

* Quy tắc tìm giới hạn tích lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

* Quy tắc tìm giới hạn thương

g) Tổng cấp số nhân lùi vô hạn

Xét cấp số nhân vô hạn u₁; u₁q; u₁q²; … u₁qⁿ; … có công bội |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn là: $S=u_1+u_{1}q+u_1{q}^2+\mathrm{....}=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

2. Các dạng toán

Dạng 1. Tính giới hạn sử dụng một vài giới hạn đặc biệt

Phương pháp giải:

Sử dụng các giới hạn đặc biệt:

$\lim u_n=0\iff \lim \left|u_n\right|=0$

$$\begin{gathered} \lim \frac{1}{n}=0;\lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right) \\ \lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right) \end{gathered}$$

$\lim q^n=\left\{\begin{array}{l}0khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.$

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \frac{1}{n^2}$

b) $\lim \frac{1}{n^2+n+3}$

c) $\lim \frac{1}{n\sqrt{n}}$

Lời giải

Áp dụng công thức tính giới hạn đặc biệt, ta có:

a) $\lim \frac{1}{n^2}=0$

b) $\lim \frac{1}{n^2+n+3}=0$

c) $\lim \frac{1}{n\sqrt{n}}=0$

Ví dụ 2: Tính các giới hạn sau:

a) $\lim {\left(\frac{1}{2}\right)}^n$

b) $\lim {\left(\frac{5}{4}\right)}^{n+1}$

c) lim (-0,999)ⁿ

Lời giải

a) $\lim {\left(\frac{1}{2}\right)}^n=0$ vì $\left|\frac{1}{2}\right|<1$

b) $\lim {\left(\frac{5}{4}\right)}^{n+1}=+\infty$ vì $\frac{5}{4}>1$

c) lim (-0,999)ⁿ = 0 vì |-0,999| < 1.

Dạng 2. Tính giới hạn hữu hạn của phân thức

Phương pháp giải:

Trường hợp lũy thừa của n: Chia cả tử và và mẫu cho n^k (với n^k là lũy thừa với số mũ lớn nhất).

Trường hợp lũy thừa mũ n: Chia cả tử và mẫu cho lũy thừa có cơ số lớn nhất.

Sử dụng một vài giới hạn đặc biệt:

$\begin{array}{l}\lim u_n=0\iff \lim \left|u_n\right|=0\\ \lim \frac{1}{n}=0;\lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right)\\ \lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right)\\ \lim q^n=\left\{\begin{array}{l}0khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.\end{array}$

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau

a) $\lim \frac{-2n^3+3n^2+4}{n^4+4n^3+n}$

b) $\lim \frac{{\left(-5\right)}^n+4^n}{{\left(-7\right)}^{n+1}+4^{n+1}}$

c) $\lim \frac{2n\sqrt{n}+1}{n^2+2\sqrt{n}-3}$

Lời giải

a) $\lim \frac{-2n^3+3n^2+4}{n^4+4n^3+n}=\lim \frac{\frac{-2n^3+3n^2+4}{n^4}}{\frac{n^4+4n^3+n}{n^4}}$

$=\lim \frac{-\frac{2}{n}+\frac{3}{n^2}+\frac{4}{n^4}}{1+\frac{4}{n}+\frac{1}{n^3}}=\frac{-0+0+4}{1+0+0}=0$

Vì $\lim \frac{2}{n}=0, \lim \frac{3}{n^2}=0,$$\lim \frac{4}{n^4}=0, \lim \frac{4}{n}=0$ và $\lim \frac{1}{n^3}=0$.

b) $\lim \frac{{\left(-5\right)}^n+4^n}{{\left(-7\right)}^{n+1}+4^{n+1}}=\lim \frac{\frac{{\left(-5\right)}^n}{{\left(-7\right)}^{n+1}}+\frac{4^n}{{\left(-7\right)}^{n+1}}}{\frac{{\left(-7\right)}^{n+1}}{{\left(-7\right)}^{n+1}}+\frac{4^{n+1}}{{\left(-7\right)}^{n+1}}}$

$=\lim \frac{\frac{1}{-7}.{\left(\frac{-5}{-7}\right)}^n+\frac{1}{-7}.{\left(\frac{4}{-7}\right)}^n}{1+{\left(\frac{4}{-7}\right)}^{n+1}}=\frac{\frac{1}{-7}.0+\frac{1}{-7}.0}{1+0}=0$

Vì  $\lim {\left(\frac{-5}{-7}\right)}^n=\lim {\left(\frac{4}{-7}\right)}^n=0$

c) $\lim \frac{2n\sqrt{n}+1}{n^2+2\sqrt{n}-3}=\lim \frac{\frac{2n\sqrt{n}+1}{n^2}}{\frac{n^2+2\sqrt{n}-3}{n^2}}$

$=\lim \frac{\frac{2}{\sqrt{n}}+\frac{1}{n^2}}{1+\frac{2}{n\sqrt{n}}-\frac{3}{n^2}}=\frac{0+0}{1+0-0}=0$

Vì $\lim \frac{2}{\sqrt{n}}=0,\lim \frac{1}{n^2}=0,$$\lim \frac{2}{n\sqrt{n}}=0,\lim \frac{3}{n^2}=0$

Ví dụ 2: Tính các giới hạn sau:

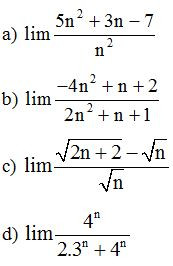
Lời giải

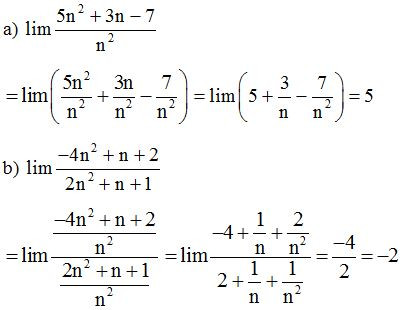
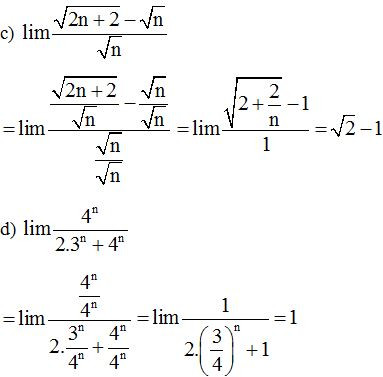
Dạng 3: Tính giới hạn hữu hạn sử dụng phương pháp liên hợp

Phương pháp giải: Sử dụng các công thức liên hợp (thường sử dụng trong các bài toán chứa căn)

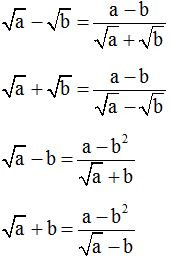
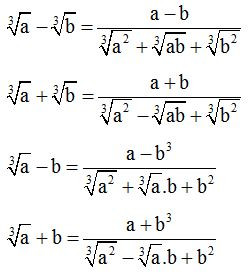
Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

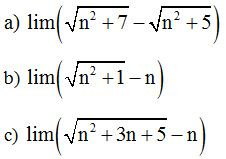
Lời giải

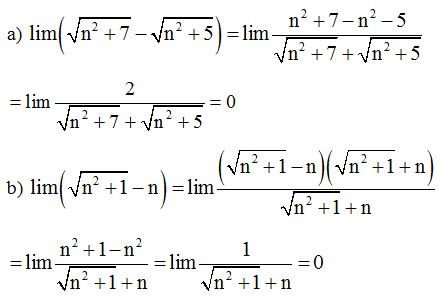
Ví dụ 2: Tính giới hạn sau: $\lim \left(\sqrt[3]{n^3+3n^2}-n\right)$

Lời giải

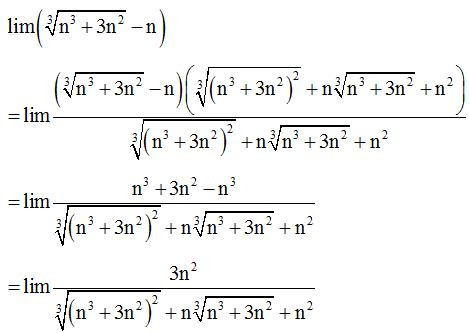
Dạng 4: Tính giới hạn ra vô cực dạng chứa đa thức hoặc căn thức

Phương pháp giải:

Rút bậc lớn nhất của đa thức làm nhân tử chung.

Sử dụng quy tắc giới hạn tới vô cực lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

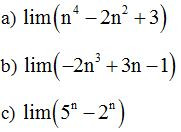
Lời giải

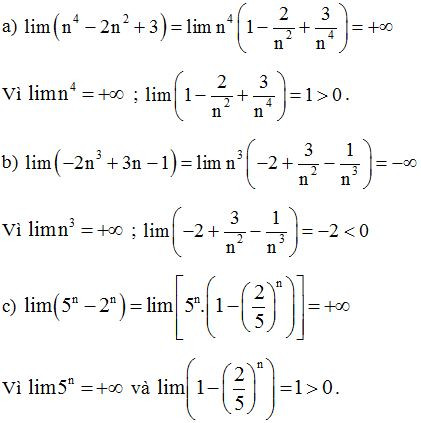
Ví dụ 2: Tính các giới hạn sau

a) $\lim \left(2n-\sqrt{n^3+2n-2}\right)$

b) $\lim \left(n^2-n\sqrt{4n+1}\right)$

Lời giải

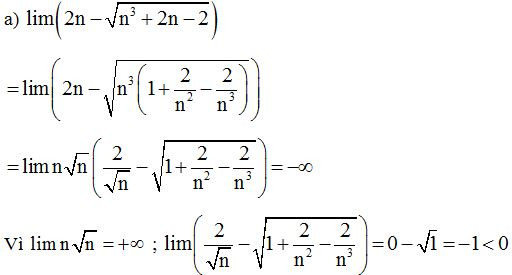
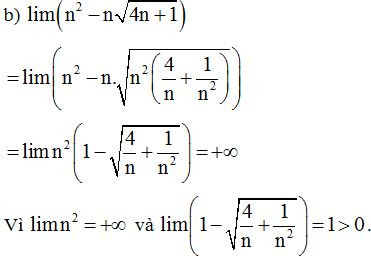
Dạng 5: Tính giới hạn ra vô cực dạng phân thức

Phương pháp giải:

Rút bậc lớn nhất của tử và mẫu ra làm nhân tử chung.

Sử dụng quy tắc giới hạn tới vô cực lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \frac{2n^4-3n^3+2}{n^3+2}$

b) $\lim \frac{\left(2n-1\right){\left(3n^2+2\right)}^3}{-2n^5+4n^3-1}$

Lời giải

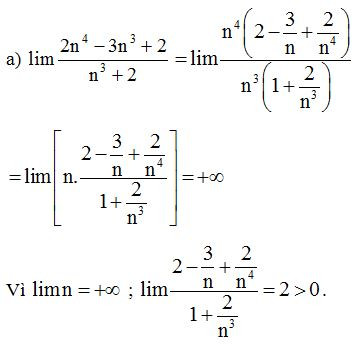
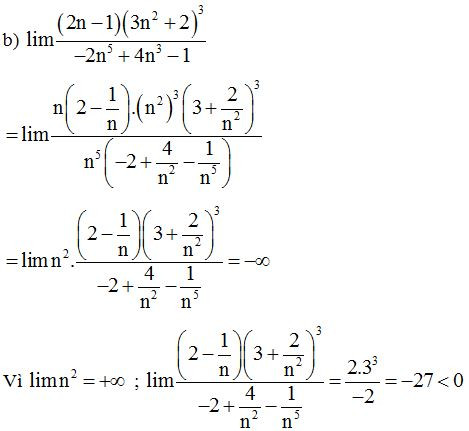
Ví dụ 2: Tính giới hạn sau $\lim \frac{3n^2-\sqrt{2n^4+3n-2}}{4n-\sqrt{3n^2+2}}$.

Lời giải

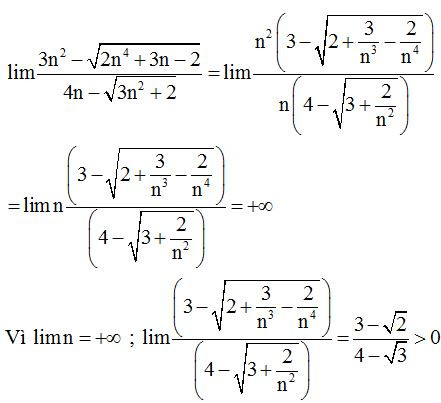
Dạng 6: Tính giới hạn sử dụng định lý kẹp

Phương pháp giải:

Sử dụng định lý kẹp và hệ quả của định lý kẹp

Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a

Hệ quả: Cho hai dãy số (u_n) và (v_n): Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \frac{{\left(-1\right)}^n}{n+4}$

b) $\lim \left(\frac{{\left(-1\right)}^n}{2^{n+1}}-\frac{1}{3^{n+1}}\right)$

Lời giải

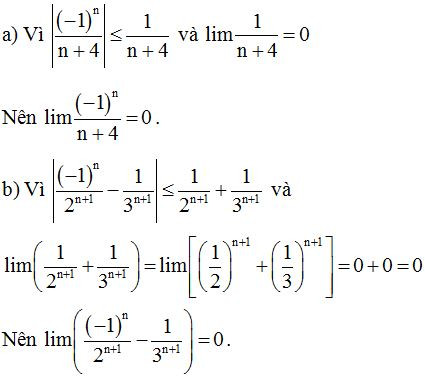
Ví dụ 2: Tính các giới hạn sau :

a) $\lim \frac{{\sin }^{2}n}{n+2}$

b) $\lim \frac{1+\cos n^3}{2n+3}$

Lời giải

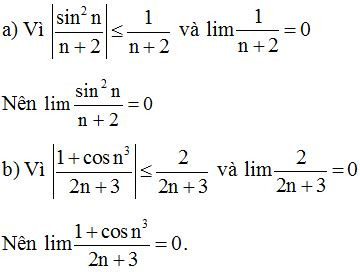
Dạng 7: Giới hạn dãy số có công thức truy hồi

Phương pháp giải:

Cho dãy số (u_n) ở dạng công thức truy hồi, biết (u_n) có giới hạn hữu hạn

Giả sử lim u_n = a (a là số thực) thì lim u_n+1 = a.

Thay a vào công thức truy hồi. Giải phương trình tìm a.

Ta được giới hạn của (u_n) là lim u_n = a.

Ví dụ minh họa:

Ví dụ 1: Tìm lim u_n biết (u_n) có giới hạn hữu hạn và $\left(u_n\right):\left\{\begin{array}{l}{u}_1=1\\ u_{n+1}=\frac{2u_n+3}{u_n+2},n\in {\mathbb{N}}^{*}\end{array}\right.$

Lời giải

Giả sử lim u_n = a, khi đó lim u_n+1 = a

Suy ra $a=\frac{2\text{a}+3}{a+2}\Rightarrow a^2+2a=2a+3$$\iff a^2=3\iff a=\pm \sqrt{3}$

Do $u_1=1>0,u_{n+1}=\frac{2u_n+3}{u_n+2}>0\forall n\in {\mathbb{N}}^{*}$ nên $a>0\Rightarrow a=\sqrt{3}$

Vậy $\lim u_n=\sqrt{3}$.

Ví dụ 2: Tìm lim u_n biết (u_n) có giới hạn hữu hạn và $\left(u_n\right):\left\{\begin{array}{l}{u}_1=\sqrt{2}\\ u_{n+1}=\sqrt{2+u_n},n\in {\mathbb{N}}^{*}\end{array}\right.$.

Lời giải

Vì $u_1=\sqrt{2}>0;u_{n+1}=\sqrt{2+u_n}>0$

Giả sử lim u_n = a (a > 0), khi đó lim u_n+1 = a

Suy ra $a=\sqrt{2+a}\iff a^2=a+2$

$$\begin{gathered} \iff a^2-a-2=0 \\ \iff \left[\begin{array}{l}a=-1\left(Loại\right)\\ a=2\end{array}\right. \end{gathered}$$

Vậy lim u_n = 2.

Dạng 8: Giới hạn của tổng vô hạn hoặc tích vô hạn

Phương pháp giải:

* Rút gọn (u_n) (sử dụng tổng cấp số cộng, cấp số nhân hoặc phương pháp làm trội)

* Rồi tìm lim u_n theo định lí hoặc dùng nguyên lí định lí kẹp.

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n): Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a

Hệ quả: Cho hai dãy số (u_n) và (v_n): Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) $\lim \left(\frac{1}{1.3}+\frac{1}{3.5}+\mathrm{...}+\frac{1}{\left(2n-1\right)\left(2n+1\right)}\right)$

b) $\lim \frac{1+2+3+4+\mathrm{...}+n}{\left(1+3+3^2+3^3+\mathrm{...}+3^n\right).\left(n+1\right)}$

Lời giải

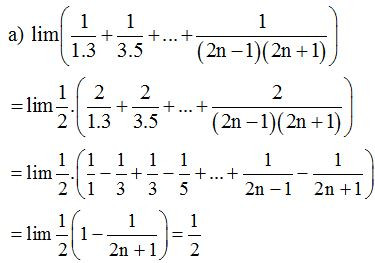
b) $L=\lim \frac{1+2+3+4+\mathrm{...}+n}{\left(1+3+3^2+3^3+\mathrm{...}+3^n\right).\left(n+1\right)}$

Xét tử số: Ta thấy 1; 2; 3; 4; … ; n là một dãy số thuộc cấp số cộng có n số hạng với u₁ = 1 và d = 1.

Tổng n số hạng của cấp số cộng: $S_n=\frac{\left(u_1+u_n\right)n}{2}=\frac{\left(1+n\right)n}{2}.$

Xét mẫu số: Ta thấy 1; 3 ; 3² ; 3³ ; … ; 3ⁿ là một dãy số thuộc cấp số nhân có (n+1) số hạng với u₁ = 1 và q = 3.

Tổng (n + 1) số hạng của cấp số nhân: $S_{n+1}=u_1.\frac{1-q^{n+1}}{1-q}=\frac{1-3^{n+1}}{1-3}=\frac{3^{n+1}-1}{2}.$

 Khi đó: $L=\lim \frac{\frac{\left(1+n\right)n}{2}}{\frac{3^{n+1}-1}{2}.(n+1)}=\lim \frac{n}{3^{n+1}-1}$

Vì $\left|\frac{n}{3^{n+1}-1}\right|=\left|\frac{n}{{3.3}^n-1}\right|<\frac{n}{3^n}<\frac{2^n}{3^n}={\left(\frac{2}{3}\right)}^n$ và $\lim {\left(\frac{2}{3}\right)}^n=0$

Nên $L=\lim \frac{n}{3^{n+1}-1}=0$

(Bằng quy nạp ta luôn có $n<2^n,\forall n\in {\mathbb{N}}^{*}$ và $3^n>1,\forall n\in {\mathbb{N}}^{*}$$\Rightarrow 3^{n+1}-3^n={2.3}^n>2>1$$\Rightarrow 3^{n+1}-1>3^n$).

Ví dụ 2: Tính giới hạn sau: $\lim \left(\frac{1}{2}\cdot \frac{3}{4}\cdot \frac{5}{6}\cdot \cdot \cdot \frac{2n-1}{2n}\right)$

Lời giải

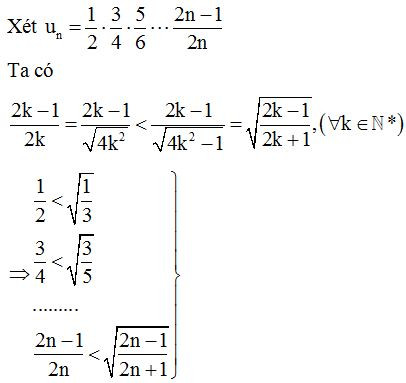
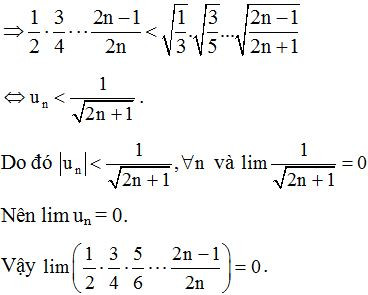
Dạng 9: Tổng cấp số nhân lùi vô hạn

Phương pháp giải:

Tổng của cấp số nhân lùi vô hạn là: $S=u_1+u_{1}q+u_1{q}^2+\mathrm{....}=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

Ví dụ minh họa:

Ví dụ 1: Tính tổng

a) $S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots$

b) $S=1+0,9+{\left(0,9\right)}^2+{\left(0,9\right)}^3+\dots$

Lời giải

a) $S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots$ là tổng cấp số nhân lùi vô hạn với u₁ = 1 và $q=\frac{1}{2}$.

Nên $S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots =\frac{1}{1-\frac{1}{2}}=2$.

b) $S=1+0,9+{\left(0,9\right)}^2+{\left(0,9\right)}^3+\dots$ là cấp số nhân lùi vô hạn với u₁ = 1 và q = 0,9.

Nên $S=1+0,9+{\left(0,9\right)}^2+{\left(0,9\right)}^3+\dots$$=\frac{1}{1-0,9}=10$.

Ví dụ 2: Biểu diễn các số thập phân vô hạn tuần hoàn ra phân số:

a) a = 0,32111...

b) b = 2,151515...

Lời giải

a) Ta có $a=0,\mathrm{32111...}=\frac{32}{100}+\frac{1}{{10}^3}+\frac{1}{{10}^4}+\frac{1}{{10}^5}+\mathrm{...}$

Vì $\frac{1}{{10}^3}+\frac{1}{{10}^4}+\frac{1}{{10}^5}+\mathrm{...}$ là tổng của cấp số nhân lùi vô hạn với $u_1=\frac{1}{{10}^3}$ và $q=\frac{1}{10}$

Nên $b=\frac{32}{100}+\frac{\frac{1}{{10}^3}}{1-\frac{1}{10}}=\frac{289}{900}$.

b) Ta có $b=2,\mathrm{151515...}=2+\frac{15}{100}+\frac{15}{{100}^2}+\frac{15}{{100}^3}+\mathrm{...}$

Vì $\frac{15}{100}+\frac{15}{{100}^2}+\frac{15}{{100}^3}+\mathrm{...}$ là tổng của cấp số nhân lùi vô hạn với $u_1=\frac{15}{100}$ và $q=\frac{1}{100}$

Nên $b=2+\frac{\frac{15}{100}}{1-\frac{1}{100}}=\frac{71}{33}$.

3. Bài tập tự luyện

Câu 1. Trong các mệnh đề sau, mệnh đề nào là mệnh đề Sai?

A. $\lim \frac{1}{\sqrt[3]{n}}=0$ .

B. $\lim \frac{{\left(-1\right)}^n}{n^2}=0$ .

C. $\lim \frac{1}{n^3}=-1$ .

D. $\lim \frac{1}{\sqrt{n}}=0$ .

Câu 2. Dãy số nào sau đây có giới hạn bằng 0?

A. ${\left(\frac{4}{3}\right)}^n$ .

B. ${\left(-\frac{4}{3}\right)}^n$ .

C. ${\left(-\frac{5}{3}\right)}^n$ .

D. ${\left(\frac{1}{3}\right)}^n$ .

Câu 3. Dãy số nào sau đây có giới hạn bằng 0?

A. $\lim \frac{n^2-2n}{5n+5n^2}$ .

B. $\lim \frac{1-2n}{5n+5}$ .

C. $\lim \frac{1-2n^2}{5n+5}$ .

D. $\lim \frac{1-2n}{5n+5n^2}$ .

Câu 4. Tính giới hạn $\lim \frac{\sin \left(n!\right)}{n^2+1}$ bằng

A. 0.

B. 1.

C. $+\infty$.

D. 2.

Câu 5. Cho dãy số (u_n) với $u_n=\frac{1+3+5+\mathrm{...}+\left(2n-1\right)}{3n^2+4}$. Khi đó lim u_n bằng

A. $\frac{1}{3}$.

B. 0.

C. $\frac{2}{3}$ .

D. 1.      

Câu 6. Cho dãy số (u_n) với $u_n=\frac{1}{1.2}+\frac{1}{2.3}+\mathrm{....}+\frac{1}{n\left(n+1\right)}$. Khi đó lim u_n bằng

A. 2

B. 1.

C. $\frac{3}{2}$.

D. Không có giới hạn.

Câu 7. Tính $\lim \left(n-\sqrt[3]{8n^3+3n+2}\right)$ bằng:

A. $+\infty$.

B. $-\infty$.

C. -1.

D. 0.

Câu 8. Tính $\lim \left(n+\sqrt[3]{4n^2-n^3}\right)$ bằng:

A. $-\frac{4}{3}$.

B. $+\infty$.

C. $\frac{4}{3}$.

D. -4.

Câu 9. Tính $\lim \frac{3^n-{2.5}^n}{7+{3.5}^n}$ bằng:

A. $\frac{2}{3}$.

B. $-\frac{1}{6}$ .

C. $\frac{1}{7}$.

D. $-\frac{2}{3}$.

Câu 10. Trong bốn giới hạn sau đây, giới hạn nào là 0?

A. $\lim \frac{2^n+3}{1-2^n}$ .

B. $\lim \frac{\left(2n+1\right){\left(n-3\right)}^2}{n-2n^3}$ .

C. $\lim \frac{1-2n^2}{n^2+2n}$ .

D. $\lim \frac{2^n+1}{{3.2}^n-3^n}$ .

Câu 11. Cho dãy số (u_n) được xác định bởi $u_1=1,u_{n+1}=\frac{2\left(2u_n+1\right)}{u_n+3}$ với mọi $n\ge 1$. Biết dãy số (u_n) có giới hạn hữu hạn, lim u_n bằng:

A. -1.

B. 2.

C. 4.

D. $\frac{2}{3}$.

Câu 12. Giới hạn dãy số (u_n) với $u_n=\frac{3n-n^4}{4n-5}$ là.

A. $-\infty$ .

B. $+\infty$ .

C. $\frac{3}{4}$ .

D. 0.

Câu 13. Chọn kết quả đúng của $\lim \frac{\sqrt{n^3-2n+5}}{3+5n}$.

A. 5.

B. $\frac{2}{5}$.

C. $-\infty$.

D. $+\infty$.

Câu 14. Tổng $S=\frac{1}{2}+\left(-\frac{1}{4}\right)+\frac{1}{8}\text{+}\mathrm{...}\text{+ }\frac{{\left(-1\right)}^{n+1}}{2^n}+\mathrm{...}$ bằng:

A. 1.

B. $\frac{1}{3}$.

C. $\frac{3}{4}$.

D. $\frac{2}{3}$.

Câu 15. Biểu diễn số thập phân 1,24545454545… như một phân số:

A. $\frac{249}{200}$

B. $\frac{137}{110}$

C. $\frac{27}{22}$

D. $\frac{69}{55}$

Bảng đáp án

Hai đường thẳng song song trong không gian và cách giải bài tập - Toán lớp 11

I. Lý thuyết ngắn gọn

1. Vị trí tương đối giữa hai đường thẳng trong không gian

- Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng

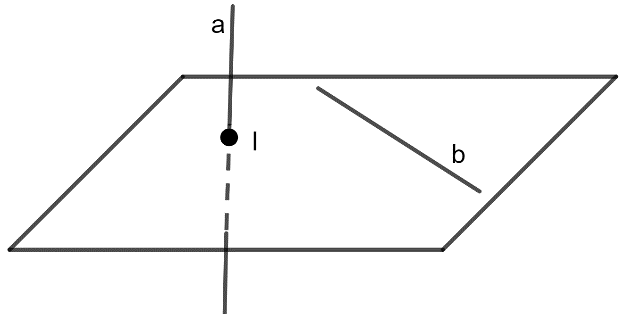
- Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng. Hai đường thẳng chéo nhau thì không có điểm chung.

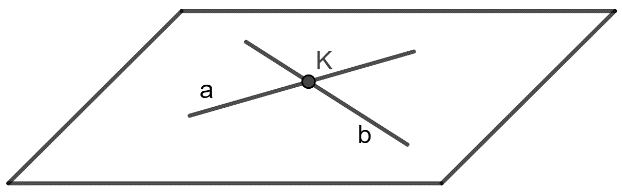
- Hai đường thẳng gọi là cắt nhau nếu chúng đồng phẳng và có một điểm chung.

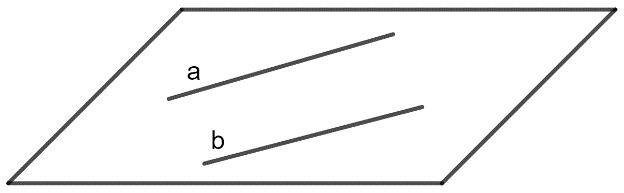
- Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.

- Như vậy, trong không gian, có 4 vị trí tương đối của hai đường thẳng, đó là: song song, trùng nhau, cắt nhau và chéo nhau.

- Khi nhắc đến hai đường thẳng phân biệt, thì ta hiểu là có 3 vị trí tương đối của hai đường thẳng đó (bỏ đi trường hợp trùng nhau).

2. Hai đường thẳng song song

a. Tính chất của hai đường thẳng song song

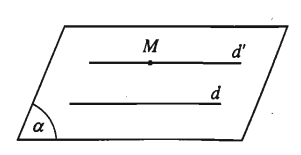
Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.

Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

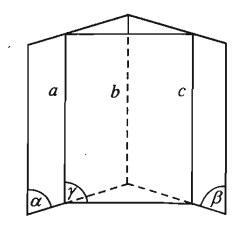
b. Định lý (về giao tuyến của ba mặt phẳng)

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Giả sử (P), (Q), (R) là ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó: $a=\left(P\right)\cap \left(R\right),$ $b=\left(Q\right)\cap \left(R\right),$ $c=\left(P\right)\cap \left(Q\right)$. Khi đó:

TH1: a, b, c đồng quy

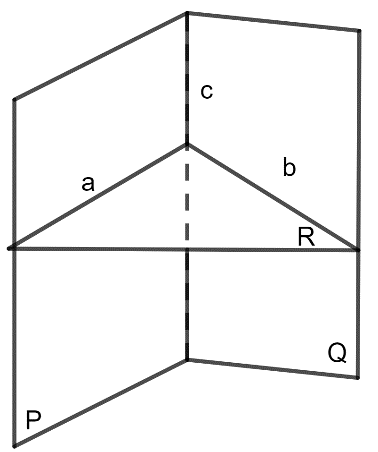
TH2: a // b // c

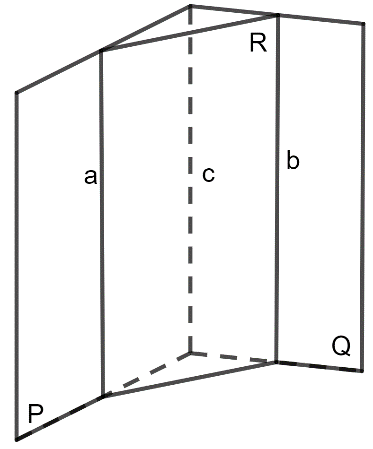
c. Hệ quả (Định lý về giao tuyến của ba mặt phẳng)

Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến (nếu có) của hai mặt phẳng nói trên sẽ song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

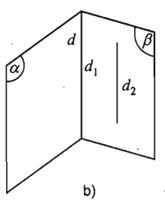
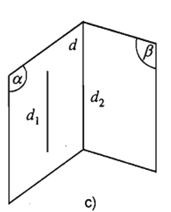
II. Các dạng bài tập về hai đường thẳng song song trong không gian

Dạng 1: Chứng minh hai đường thẳng song song

Phương pháp giải: Sử dụng một trong các cách sau

- Chứng minh hai đường thẳng đó đồng phẳng rồi áp dụng phương pháp chứng minh song song trong hình học phẳng.

- Chứng minh hai đường thẳng đó cùng song song với một đường thẳng thứ ba.

- Áp dụng định lí về giao tuyến song song.

- Áp dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABCD với đáy ABCD là hình thang với đáy AD và BC. Biết AD = a, BC = b. Gọi I, J lần lượt là trọng tâm tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q. Chứng minh MN // PQ.

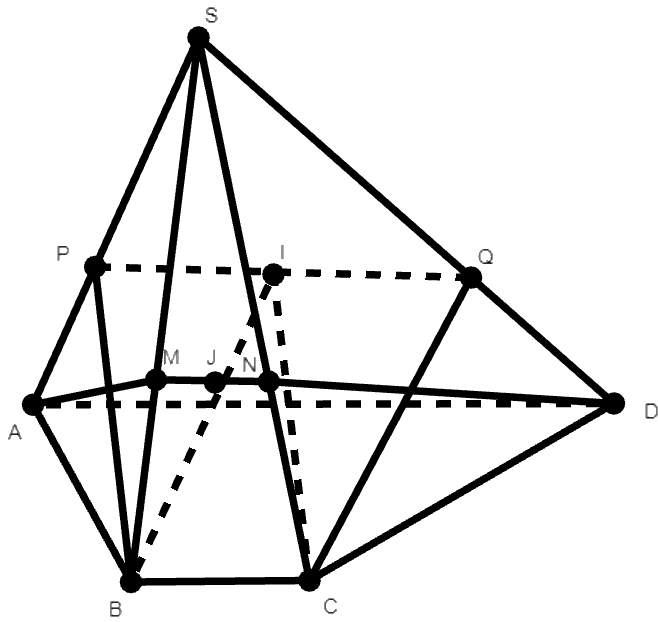
Lời giải:

Ta có: $I\in \left(SA\text{D}\right)\Rightarrow I\in \left(SA\text{D}\right)\cap \left(IBC\right)$

Lại có $\left\{\begin{array}{l}AD\subset \left(SA\text{D}\right)\\ BC\subset \left(IBC\right)\\ AD//BC\end{array}\right.$

Do đó giao tuyến của hai mặt phẳng (SAD) và (IBC) là đường thẳng qua I và song song với AD, BC.

Khi đó trong (SAD), qua I kẻ đường thẳng song song với AD, cắt SA tại P và cắt SD tại Q.

$\Rightarrow \left(SAD\right)\cap \left(IBC\right)=PQ$

$\Rightarrow PQ//AD//BC$ (1)

Chứng minh tương tự:

$$\begin{gathered} J\in \left(SBC\right)\Rightarrow J\in \left(SBC\right)\cap \left(ADJ\right) \\ \left\{\begin{array}{l}AD\subset \left(ADJ\right)\\ BC\subset \left(SBC\right)\\ AD//BC\\ \left(SBC\right)\cap \left(A\text{D}J\right)=MN\end{array}\right. \end{gathered}$$

$\Rightarrow MN//AD//BC$(2)

Do đó, từ (1) và (2) suy ra: MN // PQ.

Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N là trung điểm SA và SB.

a. Chứng minh MN // CD.

b. Gọi P là giao điểm của SC và (ADN), I là giao điểm của AN và DP. Chứng minh SI // CD.

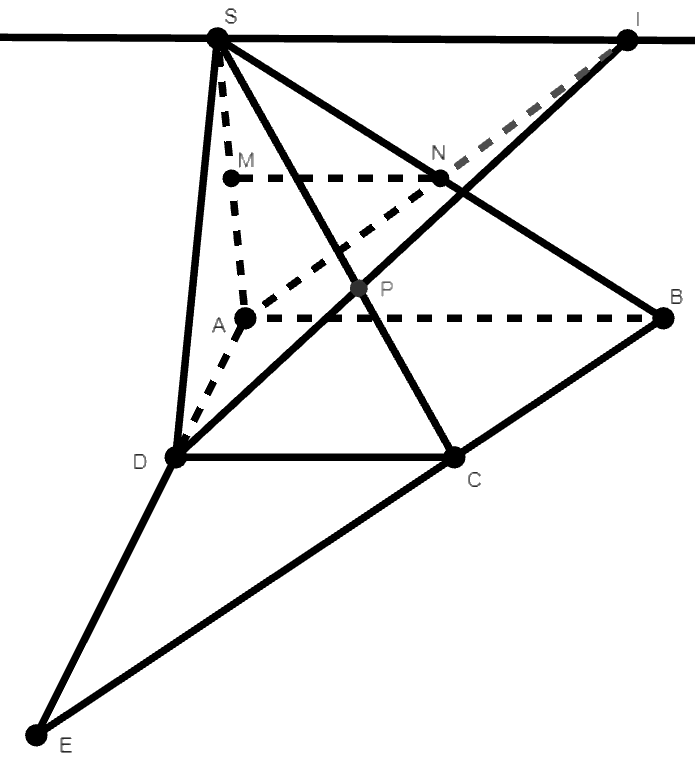
Lời giải:

a. Ta có MN là đường trung bình của tam giác SAB nên MN // AB

Lại có ABCD là hình thang nên AB // CD

Do đó: MN // CD.

b. Trong mặt phẳng (ABCD), gọi E là giao điểm của AD và BC

Trong mặt phẳng (SCD), gọi P là giao điểm của SC và DI

Ta có: $E\in AD\subset \left(A\text{D}N\right)$

$\begin{array}{l}\Rightarrow EN\subset \left(ADN\right)\\ \Rightarrow P\in \left(ADN\right)\end{array}$

Vậy $P=SC\cap \left(A\text{D}N\right)$

Do $I=AN\cap DP$

$\begin{array}{l}\Rightarrow \left\{\begin{array}{l}I\in AN\\ I\in DP\end{array}\right.\Rightarrow \left\{\begin{array}{l}I\in \left(SAB\right)\\ I\in \left(SCD\right)\end{array}\right.\\ \Rightarrow SI=\left(SAB\right)\cap \left(SC\text{D}\right)\end{array}$

Ta có:

$\begin{array}{l}\left\{\begin{array}{l}AB\subset \left(SAB\right)\\ CD\subset \left(SC\text{D}\right)\\ AB//CD\\ \left(SAB\right)\cap \left(SCD\right)=SI\end{array}\right.\\ \Rightarrow SI//CD\end{array}$

Dạng 2: Chứng minh bốn điểm đồng phẳng, ba đường thẳng đồng quy trong không gian

a. Chứng minh bốn điểm đồng phẳng

Phương pháp giải:

Chứng minh bốn điểm A, B, C, D đồng phẳng ta tìm hai đường thẳng a, b lần lượt đi qua hai trong bốn điểm trên và chứng minh a, b song song hoặc cắt nhau. Khi đó A, B, C, D thuộc mặt phẳng (a, b).

b. Chứng minh ba đường thẳng đồng quy

Phương pháp giải:

- Cách 1: Chứng minh đường thẳng thứ nhất đi qua giao điểm của hai đường thẳng còn lại.

- Cách 2: Chứng minh ba đường thẳng đôi một cắt nhau và chúng đôi một nằm trong ba mặt phẳng phân biệt

Bước 1: Xác định $\left\{\begin{array}{l}{d}_1,d_2\subset \left(P\right),d_1\cap d_2=I_1\\ d_2,d_3\subset \left(Q\right),d_2\cap d_3=I_2\\ d_3,d_1\subset \left(R\right),d_3\cap d_1=I_3\end{array}\right.$ với (P), (Q), (R) phân biệt

Bước 2: Kết luận $d_1,d_2,d_3$ đồng quy tại $I\equiv I_1\equiv I_2\equiv I_3$

Ví dụ minh họa

Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD. Gọi J là giao điểm của AC và BD.

a. Chứng minh ME, NF, SJ đồng quy.

b. Chứng minh M, N, E, F đồng phẳng.

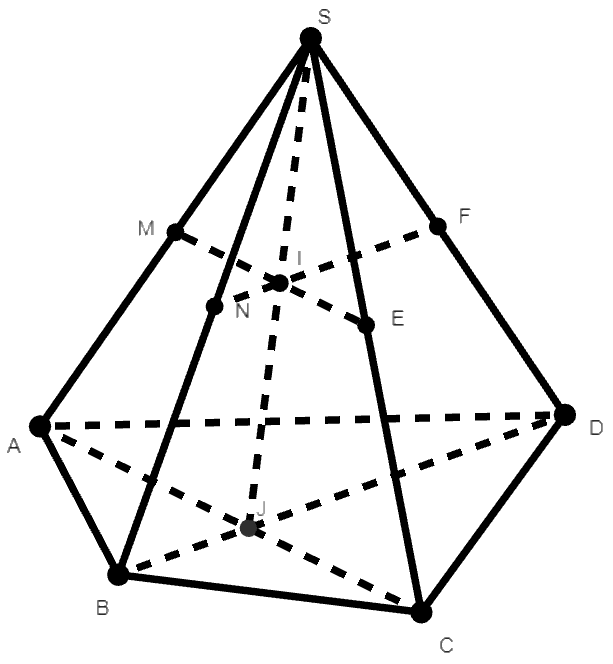
Lời giải:

a.Trong (SAC) gọi I là giao điểm của ME và SJ.

Ta có: ME là đường trung bình của tam giác SAC nên ME // AC

Suy ra MI // AC, mà M là trung điểm của SA

Nên I là trung điểm của SJ.

Suy ra: FI là đường trung bình của tam giác SJD

Suy ra FI // JD

Tương tự có: NI // JB nên N, I, F thẳng hàng

Vậy ME, NF, SJ đồng quy tại I.

b. Do I là giao điểm của ME và NF nên ME và NF xác định một mặt phẳng

Suy ra: M, N, E, F đồng phẳng.

Ví dụ 4: Cho chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi M, N, E, F lần lượt là trọng tâm các tam giác SAB, SBC, SCD, SDA. Chứng minh:

a. Bốn điểm M, N, E, F đồng phẳng.

b. ME, NF, SO đồng quy với O là tâm hình chữ nhật ABCD.

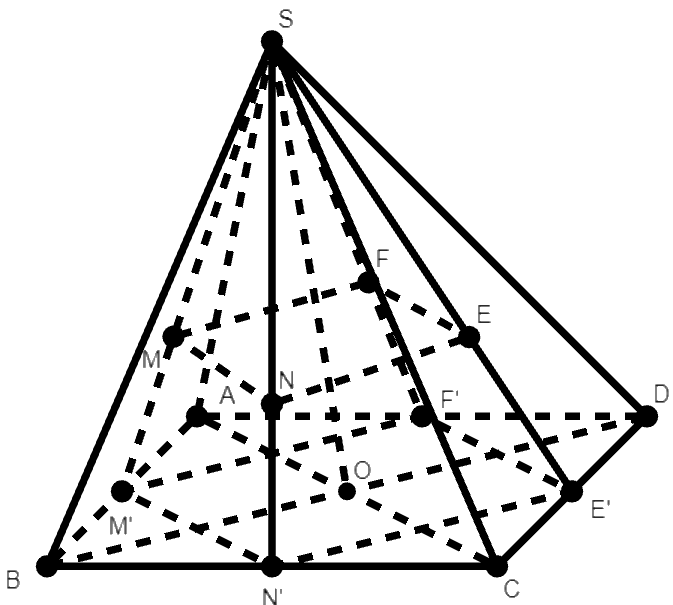
Lời giải:

a. Gọi M’, N’, E’, F’ lần lượt là trung điểm của AB, BC, CD, DA

Ta có:

$\frac{SM}{SM\text{'}}=\frac{2}{3};\frac{SN}{SN\text{'}}\text{}=\frac{2}{3}\text{}$ (tính chất trọng tâm tam giác)

$\Rightarrow \frac{SM}{SM\text{'}}=\frac{SN}{SN\text{'}}\text{}$

$\Rightarrow MN//M\text{'}N\text{'}\text{}$ (Định lý Ta – lét)

 Tương tự: $\frac{SE}{SE\text{'}}=\frac{SF}{SF\text{'}}$

$\Rightarrow EF//E\text{'}F\text{'}$(Định lý Ta – lét)

 Lại có: $\left\{\begin{array}{l}M\text{'}N\text{'}//AC\\ E\text{'}F\text{'}//AC\end{array}\right.$ (tính chất đường trung bình)

$\Rightarrow M\text{'}N\text{'}//E\text{'}F\text{'}$

Do đó: MN // EF.

Vậy bốn điểm M, N, E, F đồng phẳng.

b. Gọi I là giao điểm của ME và NF

 Dễ thấy M’N’E’F’ là hình bình hành và O là giao điểm của M’E’ và N’F’

Xét ba mặt phẳng (M’SE’), (N’SF’), (MNEF) có

$\begin{array}{l}(M\text{'}SE\text{'})\cap (N\text{'}SF\text{'})=SO\\ (M\text{'}SE\text{'})\cap \left(MNEF\right)=ME\\ (N\text{'}SF\text{'})\cap \left(MNEF\right)=NF\\ ME\cap NF=I\end{array}$

Do đó theo định lý về giao tuyến của ba mặt phẳng thì ba đường thẳng ME, NF, SO đồng quy tại I.

III. Bài tập áp dụng

1. Tự luận

Bài 1: Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AC, BD, AB, AD, BC, CD. Chứng minh P, Q, R, S đồng phẳng.

Bài 2: Cho hình chóp S.ABC. Gọi E, F lần lượt là trọng tâm các tam giác SBC và SAB. Chứng minh EF // AC.

2. Trắc nghiệm

Bài 1: Cho tứ diện ABCD. G là trọng tâm tam giác ABD, N là trung điểm của AD, M là trung điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?

A. MG // CN

B. MG và CN cắt nhau

C. MG // AB

D. MG và CN chéo nhau

Bài 2: Giả sử có ba đường thẳng a, b, c trong đó b // a và c // a. Những phát biểu nào sau đây là sai?

(1) Nếu mặt phẳng (a, b) không trùng với mặt phẳng (a, c) thì b và c chéo nhau

(2) Nếu mặt phẳng (a, b) trùng với mặt phẳng (a, c) thì ba đường thẳng a, b, c song song với nhau từng đôi một

(3) Dù cho hai mặt phẳng (a, b) và (a, c) có trùng nhau hay không, ta vẫn có b // c

A. Chỉ có (1) sai.

B. Chỉ có (2) sai

C. Chỉ có (3) sai

D. (1), (2) và (3) đều sai

Bài 3: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, AD, CD, BC. Mệnh đề nào sau đây sai?

A. MN // BD và 2MN = BD

B. MN // PQ và MN = PQ

C. MNPQ là hình bình hành

D. MP và NQ chéo nhau

Bài 4: Cho hình chóp S.ABCD. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Đường thẳng nào không song song với A’B’?

A. AB

B. CD

C. SC

D. C’D’

Bài 5: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thẳng chéo nhau khi chúng không có điểm chung

B. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau

C. Hai đường thẳng song song nhau khi chúng ở trên cùng một mặt phẳng

D. Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau

Bài 6: Cho tứ diện ABCD. Gọi I, J theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) là đường thẳng:

A. Qua I và song song với AB

B. Qua J và song song với BD

C. Qua G và song song với CD

D. Qua G và song song với BC

Bài 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang với các cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến hai mặt phẳng (SAB) và (IJG):

A. Là đường thẳng song song với AB

B. Là đường thẳng song song với CD

C. Là đường thẳng song song với đường trung bình của hình thang ABCD

D. Cả A, B, C đều đúng

Bài 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD):

A. Là đường thẳng đi qua S song song với AB, CD

B. Là đường thẳng đi qua S

C. Là điểm S

D. Là mặt phẳng (SAD)

Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:

Hệ thống kiến thức Toán lớp 11 Giữa học kì 2

TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án

Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất

Bài tập Toán lớp 11 Học kì 2 có đáp án

Các dạng bài tập Toán lớp 11 Học kì 2