Hệ thống kiến thức Toán lớp 11 Học kì 1

Hệ thống kiến thức Toán lớp 11 Học kì 1

A. ĐẠI SỐ VÀ GIẢI TÍCH

2022

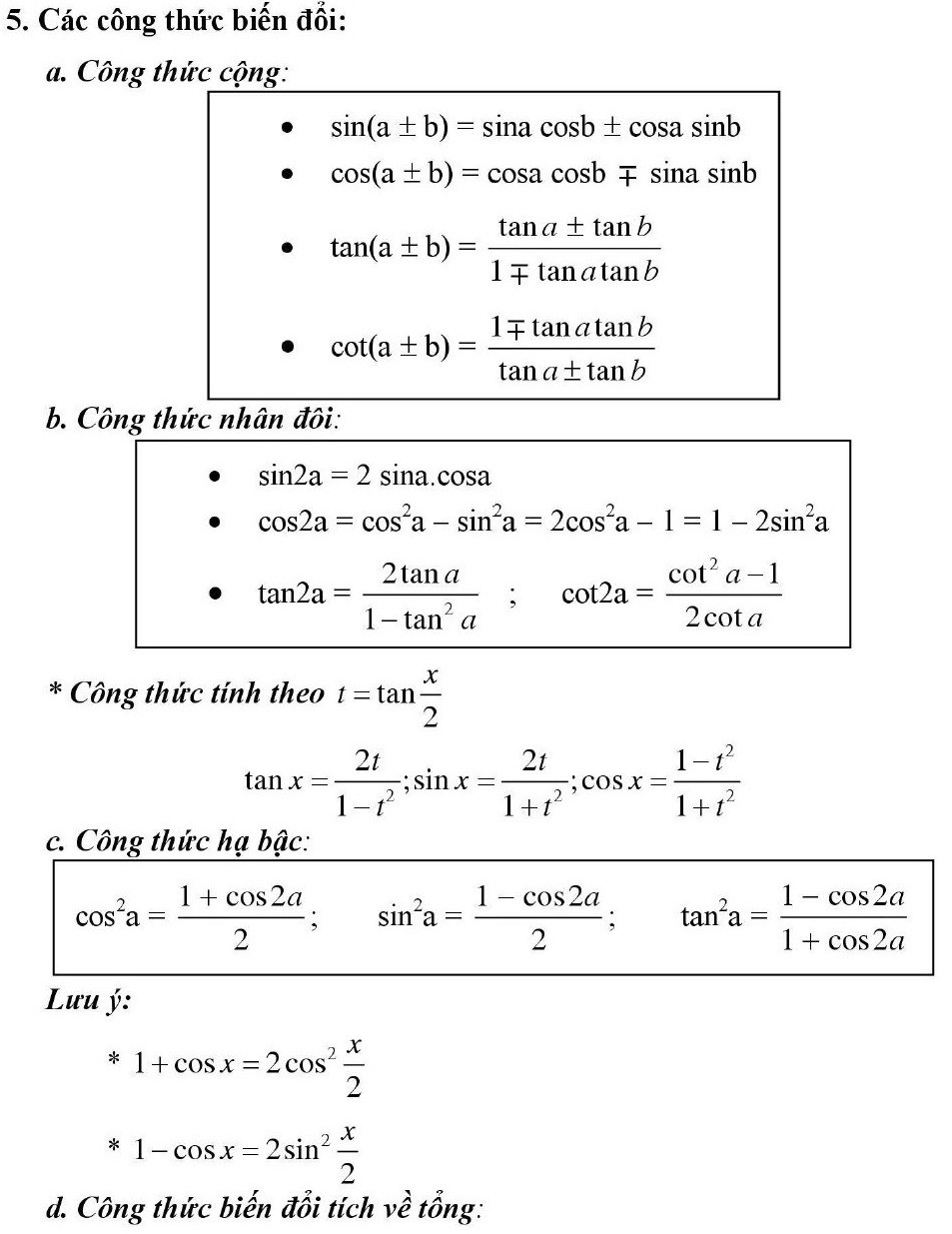
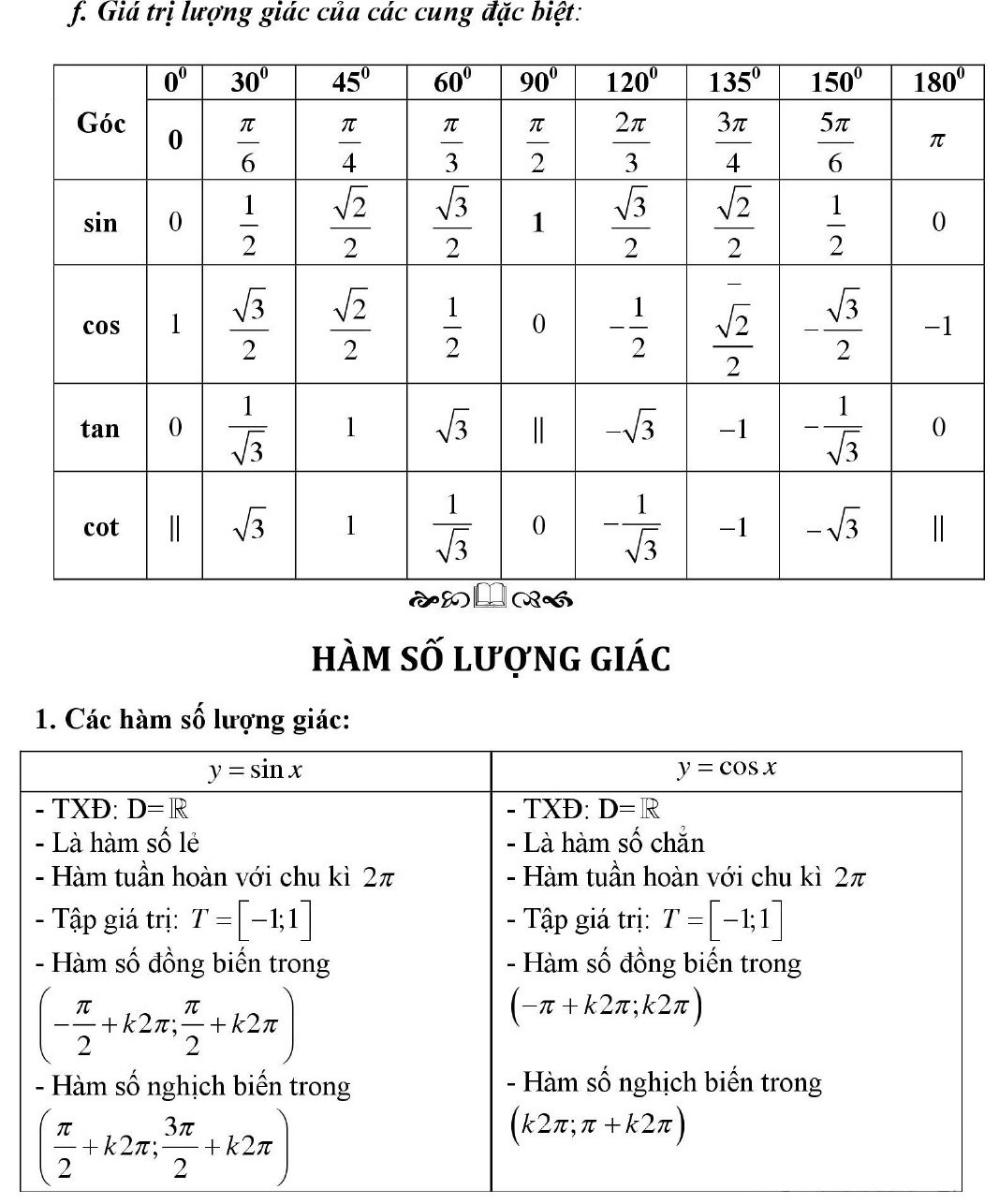
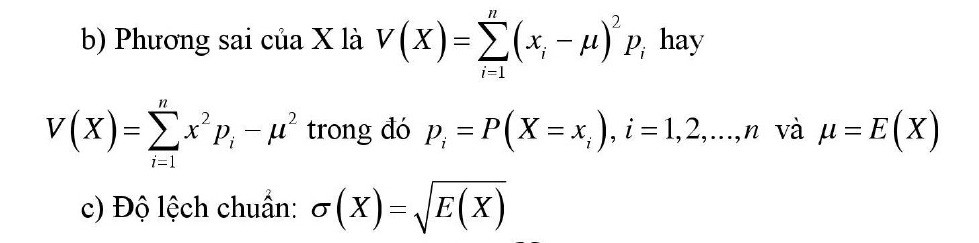
B. HÌNH HỌC

Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

1. Định nghĩa phép biến hình

- Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.

- Nếu kí hiệu phép biến hình là F thì ta viết F(M) = M’ hay M’ = F(M) và gọi M’ là ảnh của điểm M qua phép biến hình F.

- Nếu ℋ  là một hình nào đó trong mặt phẳng thì ta kí hiệu ℋ ' = F(ℋ) là tập các điểm M’ = F(M), với mọi điểm M thuộc ℋ. Khi đó, ta nói F là biến hình ℋ  thành hình ℋ ', hay hình ℋ ' là ảnh của hình ℋ  qua phép biến hình F.

- Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.

Ví dụ. Cho trước đường thẳng d, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho M’ đối xứng với M qua d.

Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên là một phép biến hình vì chỉ có duy nhất 1 điểm M’ thỏa mãn yêu cầu.

2. Định nghĩa phép tịnh tiến

- Định nghĩa: Trong mặt phẳng, cho vectơ $\overrightarrow{v}$. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow{MM\text{'}}=\overrightarrow{v}$ được gọi là phép tịnh tiến theo vectơ $\overrightarrow{v}$.

- Phép tịnh tiến theo vectơ  thường được kí hiệu là được gọi là vectơ tịnh tiến.

Vậy: $T_{\overrightarrow{v}}\left(M\right)=M\text{'}\iff \overrightarrow{MM\text{'}}=\overrightarrow{v}$.

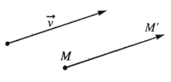
- Phép tịnh tiến theo vectơ – không chính là phép đồng nhất.

- Ví dụ 1. Cho hình vẽ sau:

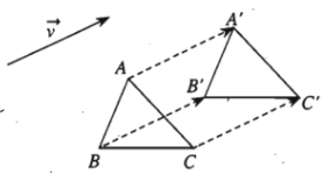
Ta có: $T_{\overrightarrow{v}}\left(A\right)=A\text{'};$$\hspace{0.17em}{T}_{\overrightarrow{v}}\left(B\right)=B\text{'};T_{\overrightarrow{v}}\left(C\right)=C\text{'}\hspace{0.17em}$.

3. Tính chất của phép tịnh tiến

- Tính chất 1.  Nếu $T_{\overrightarrow{v}}\left(M\right)=M\text{'};$$T_{\overrightarrow{v}}\left(N\right)=N\text{'}$ thì $\overrightarrow{M\text{'}N\text{'}}=\overrightarrow{MN}$ và từ đó suy ra M’N’ = MN.

Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

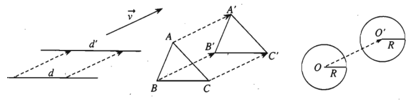
- Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

4. Biểu thức tọa độ của phép tịnh tiến

Trong mặt phẳng tọa độ Oxy cho vectơ $\overrightarrow{v}(a;b)$. Với mỗi điểm M(x ; y) ta có M’(x’ ; y’) là ảnh của điểm M qua tịnh tiến theo vectơ $\overrightarrow{v}$.

Khi đó:  

$$\begin{gathered} \overrightarrow{MM\text{'}}=\overrightarrow{v} \\ \iff \left\{\begin{array}{c}x\text{'}-x=a\\ y\text{'}-y=b\end{array}\right. \\ \Rightarrow \left\{\begin{array}{c}x\text{'}=x+a\\ y\text{'}=y+b\end{array}\right. \end{gathered}$$

đây chính là biểu thức tọa độ của phép tịnh tiến $T_{\overrightarrow{v}}$.

Ví dụ. Trong mặt phẳng tọa độ Oxy, cho điểm A(1 ; – 2). Phép tịnh tiến theo vectơ biến A thành điểm A’ có tọa độ là bao nhiêu?

Lời giải:

Gọi tọa độ điểm A’ = (x’; y’).

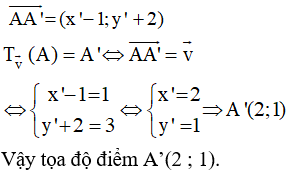
5. Định nghĩa của phép đối xứng trục

- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

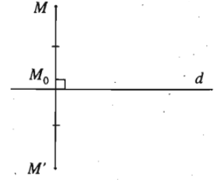
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.

Phép đối xứng trục d thường được kí hiệu là Đ_d.

- Nếu hình ℋ ' là ảnh của hình ℋ  qua phép đối xứng trục d thì ta còn nói ℋ  đối xứng với ℋ ' qua d, hay ℋ  và ℋ ' đối xứng với nhau qua d.

- Nhận xét:

1) Cho đường thẳng d. Với mỗi điểm M, gọi M₀ là hình chiếu vuông góc của M

trên đường thẳng d. Khi đó: M’ = Đ_d(M) $\iff \overrightarrow{M_{0}M\text{'}}=-\overrightarrow{M_{0}M}$

2) M’ = Đ_d(M) $\iff$M = Đ_d(M’).

6. Biểu thức tọa độ của phép đối xứng trục

1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’ ; y’) thì $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Ox. 

2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’; y’) thì $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Oy.

Ví dụ. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.

Lời giải:

Gọi Đ_Ox(M) = A(x ; y) và Đ_Oy(M) = B(a; b)

Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:

$$\begin{gathered} \left\{\begin{array}{c}x=2\\ y=-4\end{array}\right. \\ \Rightarrow A(2;-4) \end{gathered}$$

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:

$\left\{\begin{array}{c}a=-2\\ b=4\end{array}\Rightarrow B(-2;4)\right.$

7. Tính chất của phép đối xứng trục

- Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

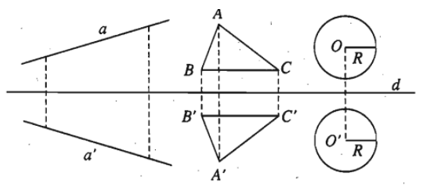
Ví dụ. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)

(x – 2)² + (y – 3)² = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?

Lời giải:

Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.

Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.

Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)

Do đó, phương trình đường tròn (C’) là:

(x – 2)² + (y + 3)² = 36.

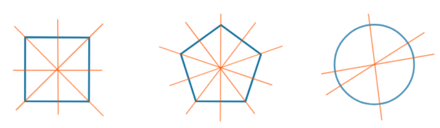
8. Trục đối xứng của một hình

- Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.

Khi đó, ta nói ℋ là hình có trục đối xứng.

- Ví dụ 3. Các hình sau có trục đối xứng

9. Định nghĩa của phép đối xứng tâm

- Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác điểm I thành điểm M’ sao cho I là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm I.

Điểm I được gọi là tâm đối xứng.

Phép đối xứng tâm I thường được kí hiệu là Đ_I.

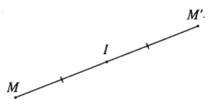
- Nếu hình ℋ ' là ảnh của hình ℋ  qua Đ_I thì ta còn nói ℋ  đối xứng với ℋ ' qua tâm I, hay ℋ  và ℋ ' đối xứng với nhau qua I.

Từ định nghĩa trên ta suy ra, M’ = Đ_I(M) $\iff \overrightarrow{IM\text{'}}=-\overrightarrow{IM}$.

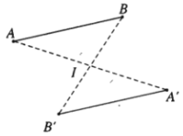
- Ví dụ 1. Cho hình vẽ sau. Các điểm A và B là ảnh của điểm A’ và B’ qua phép đối xứng tâm I và ngược lại.

10. Biểu thức tọa độ của phép đối xứng qua gốc tọa độ

Trong hệ tọa độ Oxy, cho M(x ; y), M’= Đ_O(M) = (x’; y’). Khi đó:

 $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua gốc tọa độ.

- Ví dụ. Trong mặt phẳng tọa độ Oxy cho điểm A(7 ; – 4). Tìm ảnh của điểm A qua phép đối xứng tâm O. 

Lời giải:

Gọi A’(x’; y’) là ảnh của điểm A qua  phép đối xứng tâm O. 

Áp dụng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có:

$$\begin{gathered} \left\{\begin{array}{c}x\text{'}=-7\\ y\text{'}=-(-4)=4\end{array}\right. \\ \hspace{0.17em}\Rightarrow A\text{'}(-7;4) \end{gathered}$$

11. Tính chất của phép đối xứng tâm

- Tính chất 1. Nếu Đ_I(M) = M’ và Đ_I(N) = N’ thì $\overrightarrow{M\text{'}N\text{'}}=-\overrightarrow{MN}$, từ đó suy ra M’N’ = MN.

Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

- Ví dụ. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + y – 2 = 0. Tìm ảnh của d qua phép đối xứng tâm I(1; 2).

Lời giải:

Giả sử phép đối xứng tâm I(1 ; 2) biến điểm  thành điểm M’(x’ ; y’).

Khi đó I là trung điểm của MM’. Áp dụng công thức tọa độ trung điểm ta có:

$$\begin{gathered} \left\{\begin{array}{l}{x}^{\text{'}}=2.1-x=2-x\\ y^{\text{'}}=2.2-y=4-y\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2-x^{\text{'}}\\ y=4-y^{\text{'}}\end{array}\right. \end{gathered}$$

Vì điểm M thuộc d nên: x + y – 2 = 0    (2).

Thay (1) vào (2) ta được:

(2 – x’) + (4 – y’) – 2 = 0 hay – x’ – y’ + 4 = 0.

Do đó, phương trình đường thẳng d’ là – x – y + 4 = 0 hay x + y – 4 =0.

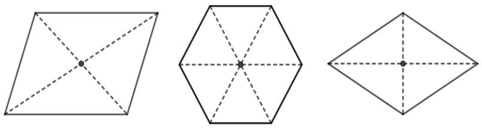
12. Tâm đối xứng của một hình

Định nghĩa. Điểm I được gọi là tâm đối xứng của hình ℋ nếu phép đối xứng tâm I biến hình ℋ  thành chính nó.

- Khi đó, ta nói ℋ  là hình có tâm đối xứng.

- Ví dụ 4. Các hình sau đây đều có tâm đối xứng:

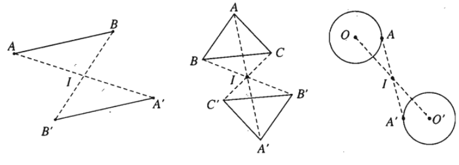
13. Định nghĩa của phép quay

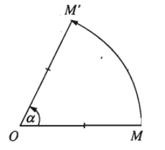
- Định nghĩa: Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.

- Điểm O được gọi là tâm quay, α được gọi là góc quay của phép quay đó.

Phép quay tâm O góc α được kí hiệu là Q_{(O, α).}

- Nhận xét:

1) Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược với chiều quay của kim đồng hồ.

2) Với k là số nguyên ta luôn có:

Phép quay $Q_{(O,k2\pi )}$ là phép đồng nhất.

Phép quay $Q_{(O,(2k\text{}+1\left)\pi \right)}$ là phép đối xứng tâm O.

14. Tính chất của phép quay

- Tính chất 1. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.

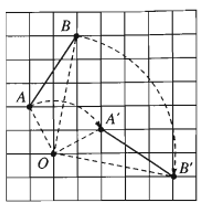
Phép quay tâm O, góc (OA, OA’) biến điểm A thành A’, B thành B’. Khi đó ta có A’B’ = AB.

- Tính chất 2. Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

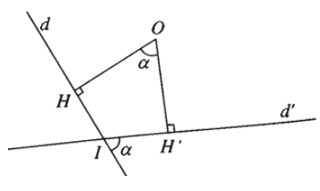
- Nhận xét: Phép quay góc α với , biến đường thẳng d thành đường thẳng d’ sao cho góc giữa d và d’ bằng α (nếu $0<\alpha \le \frac{\pi }{2}$), hoặc bằng $\mathrm{\pi }-\mathrm{\alpha }$ (nếu  $\frac{\pi }{2}\le \alpha <\pi )$

15. Khái niệm về phép dời hình

- Định nghĩa: Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.

Nếu phép dời hình F biến các điểm M, N lần lượt thành các điểm M’; N’ thì

MN = M’N’.

- Nhận xét:

1) Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.

2) Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình.

- Ví dụ 1. Vì phép tịnh tiến và phép đối xứng tâm là phép dời hình nên thực hiện liên tiếp phép tịnh tiến theo vectơ  và phép đối xứng tâm O ta được một phép dời hình.

16. Tính chất của phép dời hình

Phép dời hình:

1) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.

2) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.

3) Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.

4) Biến đường tròn thành đường tròn có cùng bán kính.

- Chú ý:

a) Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

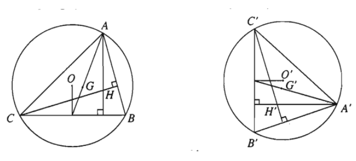
b) Phép dời hình biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.

- Ví dụ . Cho đường tròn (C) có phương trình (x + 4)² + (y – 3)² = 49. Thực hiện liên tiếp phép đối xứng trục qua đường thẳng d và phép quay tâm O góc quay 90⁰ ta được đường tròn (C’).

Bán kính đường tròn (C’) là: R’ = R = 7.

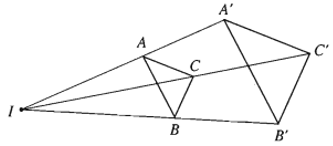
17. Khái niệm hai hình bằng nhau

- Định nghĩa. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

- Ví dụ.

a)  Qua phép tịnh tiến theo vectơ  biến tam giác ABC thành tam giác A’B’C’. Sau đó, ta thực hiện tiếp phép đối xứng trục qua đường thẳng d biến tam giác A’B’C’ thành tam giác A”B”C”. Khi đó: ∆ABC = ∆A”B”C”.

b) Hình ảnh dưới đây cho ta hai hình bằng nhau:

18. Định nghĩa của phép vị tự

- Cho điểm O và số k ≠ 0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow{OM\text{'}}=k.\overrightarrow{OM}$ được gọi là phép vị tự tâm O, tỉ số k.

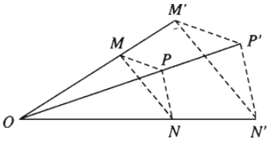
Phép vị tự tâm O tỉ số k thường được kí hiệu là V_{(O, k)}.

- Nhận xét:

1) Phép vị tự biến tâm vị tự thành chính nó.

2) Khi k = 1, phép vị tự là phép đồng nhất.

3) Khi k = -1, phép vị tự là phép đối xứng qua tâm vị tự.

4) M’ = V_{(O, k)}(M) $\iff M=V_{\left(O,\frac{1}{k}\right)}(M\text{'})$.

19. Tính chất của phép vị tự

- Tính chất 1. Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì $\overrightarrow{M\text{'}N\text{'}}=k.\overrightarrow{MN}$ và M’N’ = |k|.MN.

- Tính chất 2.

Phép vị tự tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

d) Biến đường tròn bán kính R thành đường tròn có bán kính |k|.R.

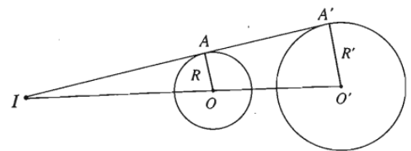
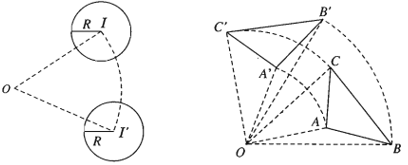
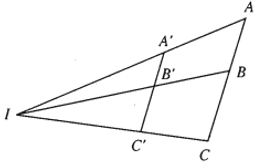
20. Tâm vị tự của hai đường tròn.

- Định lí: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.

Tâm của phép vị tự được gọi là tâm vị tự của hai đường tròn.

- Cách tìm tâm vị tự của hai đường tròn.

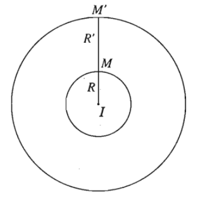
Cho hai đường tròn (I ; R) và (I’; R’) có ba trường hợp xảy ra:

+ Trường hợp I trùng với I’

Khi đó, phép vị tự tâm I tỉ số $\frac{R\text{'}}{R}$ và phép vị tự tâm I tỉ số $-\frac{R\text{'}}{R}$ biến đường tròn

(I ; R) thành đường tròn (I ; R’).

+ Trường hợp I khác I’ và R ≠ R’

Lấy điểm M bất kì thuộc đường tròn (I ; R), đường thẳng qua I’ song song với IM cắt đường tròn (I’ ; R’) tại M’ và M”.

Giả sử M, M’ nằm cùng phía đối với đường thẳng II’ còn M, M” nằm khác phía đối với đường thẳng II’.

Giả sử đường thẳng MM’ cắt đường thẳng II’ tại điểm O nằm ngoài đoạn thẳng II’, còn đường thẳng MM” cắt đường thẳng II’ tại điểm O₁ nằm trong đoạn thẳng II’.

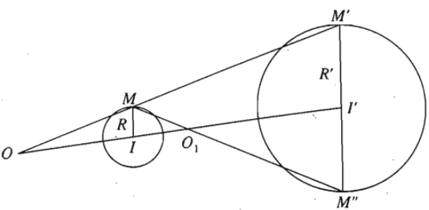
Khi đó, phép vị tự tâm O tỉ số $k=\frac{R\text{'}}{R}$ và phép vị tự tâm O₁ tỉ số $k_1=-\frac{R\text{'}}{R}$ sẽ biến đường tròn (I ; R) thành đường tròn (I’; R’).

Ta gọi O là tâm vị tự ngoài còn O₁ là tâm vị tự trong của hai đường tròn nói trên.

+ Trường hợp I khác I’ và R = R’.

Khi đó, MM’ // II’ nên chỉ có phép vi tự tâm O₁ tỉ số $k=\frac{-R}{R}=-1$ biến đường tròn (I; R) thành đường tròn (I’ ; R’). Đây chính là phép đối xứng tâm O₁.

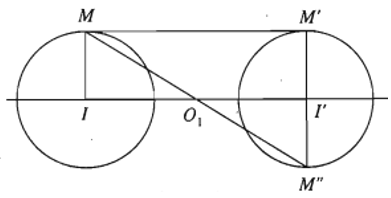
Ví dụ 1. Cho hai đường tròn (C): (x – 2)² + (y – 1)² = 4 và (C’): (x – 8)² + (y – 4)² = 16. Xác định tâm vị tự của hai đường tròn?

Lời giải:

Đường tròn (C) có tâm I(2 ; 1),bán kính R = 1;

Đường tròn (C’) có tâm I’(8 ; 4), bán kính R’ = 4.

Do I  ≠  I’ và R ≠ R’ nên có hai phép vị tự V_{(J, 2)} và V_{(J, -2)} biến (C) thành (C’).

Gọi J(x ; y)

Với k = 2 khi đó:

$$\begin{gathered} \overrightarrow{JI\text{'}}=2\overrightarrow{JI} \\ \iff \left\{\begin{array}{l}8-x=2\left(2-x\right)\\ 4-y=2\left(1-y\right)\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-4\\ y=-2\end{array}\right. \end{gathered}$$

Suy ra: J(– 4; – 2)

Tương tự với k = – 2, tính có J’(4; 2).

Vậy có 2 phép vị tự thỏa mãn đầu bài.

21. Định nghĩa phép đồng dạng

- Định nghĩa: Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0), nếu với hai điểm M, N bất kì và ảnh M’, N’ tương ứng của chúng ta luôn có M’N’ = kMN.

- Nhận xét

(1) Phép dời hình là phép đồng dạng tỉ số 1.

(2) Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

22. Tính chất phép đồng dạng

Phép đồng dạng tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

d) Biến đường tròn bán kính R thành đường tròn có bán kính kR.

- Chú ý.

a) Nếu một phép đồng dạng biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

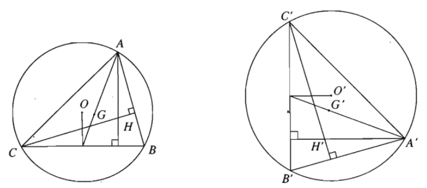
b) Phép đồng dạng biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thảng đỉnh, biến cạnh thành cạnh.

Ví dụ. Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn (C) và (C’) có phương trình x² + y² – 4y – 5 = 0 và x² + y² – 2x + 2y – 14 = 0. Gọi (C’) là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị k là ?

Lời giải:

Đường tròn (C) có tâm I(0 ; 2) bán kính R = 3.

Đường tròn (C’) có tâm I’(1 ; – 1) bán kính R’ = 4.

Ta có (C’) là ảnh của (C) qua phép đồng dạng tỉ số k nên : 4 = 3k

Suy ra : $k=\frac{4}{3}$ .

Vậy $k=\frac{4}{3}$.

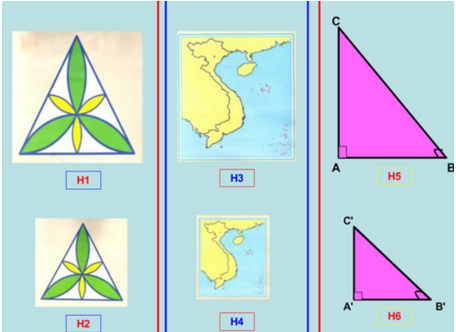
23. Hình đồng dạng

- Định nghĩa. Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.

- Ví dụ. Các hình sau đôi một đồng dạng với nhau.

Chương 2: Đường thằng và mặt phẳng trong không gian. Quan hệ song song

1. Đường thẳng và mặt phẳng trong không gian

1.1 Mặt phẳng

- Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.

- Để kí hiệu mặt phẳng, ta thường dùng các chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ngoặc ( ). Ví dụ: mp(P), mp(Q), mp(α), mp(β)…

1.2 Điểm thuộc mặt phẳng.

Cho điểm A và mặt phẳng (α).

- Khi điểm A thuộc mặt phẳng (α) ta nói A nằm trên (α) hay (α) chứa A, hay (α) đi qua A và kí hiệu là $A\in \left(\alpha \right)$.

- Khi điểm A không thuộc mặt phẳng (α) ta nói điểm A nằm ngoài (α) hay (α)  không chứa A và kí hiệu là $A\notin \left(\alpha \right)$.

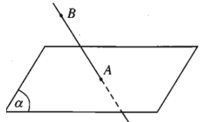
Hình trên cho ta hình biểu diễn của điểm A thuộc mặt phẳng , còn điểm B không thuộc (α).

1.3 Hình biểu diễn của một hình trong không gian

Để nghiên cứu hình học không gian người ta thường vẽ các hình không gian lên bảng, lên giấy. Ta gọi hình vẽ đó là hình biểu diễn của một hình không gian.

- Dưới đây là một vài hình biểu diễn của hình hộp chữ nhật.

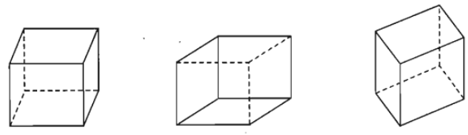
Để vẽ hình biểu diễn của một hình trong không gian người ta dựa vào những quy tắc sau đây:

- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.

- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.

- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.

2. Các tính chất thừa nhận về đường thẳng và mặt phẳng trong không gian

- Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt

- Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

Một mặt phẳng hoàn toàn xác định nếu biết nó đi qua ba điểm không thẳng hàng. Ta kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng A, B, C là mặt phẳng (ABC) hoặc mp(ABC) hoặc (ABC).

- Tính chất 3. Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (α) thì ta nói đường thẳng d nằm trong (α) hay (α) chứa d và kí hiệu là $d\subset \left(\alpha \right)$ hay $\left(\alpha \right)\supset d$.

- Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng, còn nếu không có mặt phẳng nào chứa các điểm đó thì ta nói chúng không đồng phẳng.

- Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.

Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.

Đường thẳng chung d của hai mặt phẳng phân biệt (α) và (β) được gọi là giao tuyến của (α) và (β) và kí hiệu là $d=\left(\alpha \right)\cap \left(\beta \right)$.

- Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

3. Cách xác định mặt phẳng

3.1) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.

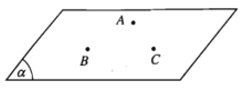
3.2) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.

Cho đường thẳng d và điểm A không thuộc d. Khi đó điểm A và đường thẳng d xác định một mặt phẳng, kí hiệu là mp(A, d) hay (A, d) hoặc mp(d, A) hay (d, A).

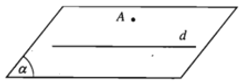
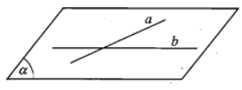
3.3) Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.

Cho hai đường thẳng cắt nhau a và b. Khi đó hai đường thẳng a và b xác định một mặt phẳng và kí hiệu là mp(a, b) hay (a, b) hoặc mp(b, a) hay (b, a).

4. Hình chóp và hình tứ diện

4.1. Hình chóp

Trong mp(α) cho đa giác lồi A₁A₂…A_n. Lấy điểm S nằm ngoài (α). Lần lượt nối S với các đỉnh A₁, A₂,..,A_n ta được n tam giác SA₁A₂, SA₂A₃,…, SA_nA₁.

Hình gồm đa giác A₁A₂…A_n và n tam giác SA₁A₂, SA₂A₃,…, SA_nA₁ gọi là hình chóp, kí hiệu là S.A₁A₂…A_n.

Ta gọi S là đỉnh và đa giác A₁A₂…A_n là mặt đáy. Các tam giác SA₁A₂, SA₂A₃,…, SA_nA₁ gọi là các mặt bên, các đoạn SA₁, SA₂, …, SA_n là các cạnh bên; các cạnh của đa giác đáy gọi là các cạnh đáy của hình chóp.

Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,.. lần lượt là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác…

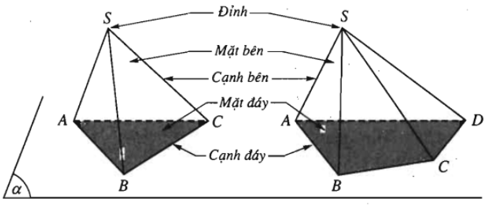
4.2. Hình tứ diện

Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD gọi là hình tứ diện (hay tứ diện) và được kí hiệu là ABCD.

Các điểm A, B, C, D gọi là các đỉnh của tứ diện.

Các đoạn thẳng AB, BC, CD, DA, CA, BD gọi là các cạnh của tứ diện.

Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện.

Các tam giác ABC, ACD, ABD, BCD gọi là các mặt của tứ diện. Đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.

Hình tứ diện có 4 mặt là các tam giác đều gọi là hình tứ diện đều.

- Chú ý. Khi nói đến tam giác ta có thể hiểu là tập hợp các điểm thuộc các cạnh hoặc cũng có thể hiểu là tập hợp các điểm thuộc các cạnh và các điểm trong của tam giác đó. Tương tự có thể hiểu như vậy đối với đa giác.

4.3. Một số ví dụ

Ví dụ 1.Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB // CD).

Tìm giao tuyến của hai mặt phẳng:

a) (SAC) và (SBD).

b) (SAD) và (SBC).

Lời giải:

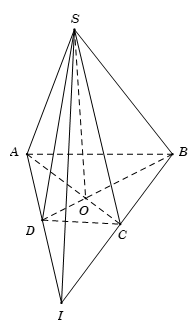
a) Trong mp(ABCD), gọi O là giao điểm của AC  và BD.

Ta có S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD).

Lại có:  

$\left\{\begin{array}{l}O\in AC\subset \left(SAC\right)\Rightarrow O\in \left(SAC\right)\\ O\in BD\subset \left(SBD\right)\Rightarrow O\in \left(SBD\right)\end{array}\right.$

Suy ra, O là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD).

Vậy giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.

b) Trong mp(ABCD), gọi I là giao điểm của AD và BC.

Ta có S là điểm chung thứ nhất của hai mặt phẳng (SAD) và (SBC).

Lại có:  $\left\{\begin{array}{l}I\in AD\subset \left(SAD\right)\Rightarrow I\in \left(SAD\right)\\ I\in BC\subset \left(SBC\right)\Rightarrow I\in \left(SBC\right)\end{array}\right.$

Suy ra, I là điểm chung thứ hai của hai mặt phẳng (SAD) và (SBC).

Vậy giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI.

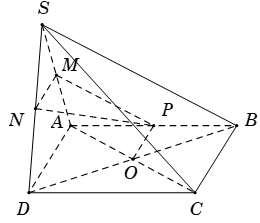
Ví dụ 2. Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD)?

Lời giải:

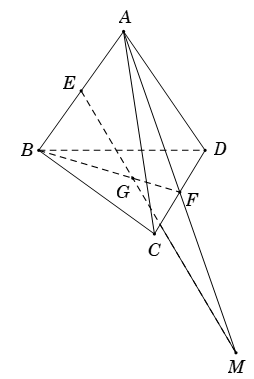
Vì G là trọng tâm tam giác BCD, F là trung điểm của CD nên

Ta có E là trung điểm của AB nên .

Chọn mp phụ chứa EG là (ABF)

+ Tìm giao tuyến của mp(ABF) và mp(ACD) ta có:

A là điểm chung thứ nhất.

$\left\{\begin{array}{l}F\in \left(A\text{}BF\right)\\ F\in CD\subset \left(ACD\right)\Rightarrow F\in \left(ACD\right)\end{array}\right.$

Suy ra F là điểm chung thứ hai .

Do đó, giao tuyến của mp(ABF) và mp(ACD) là AF.

Trong mp(ABF), kéo dài AF cắt EG tại M. Khi đó, M là giao điểm của EG và mp(ACD).

5. Vị trí tương đối của hai đường thẳng trong không gian

Cho hai đường thẳng a và b trong không gian. Khi đó có thể xảy ra một trong các trường hợp sau:

- Trường hợp 1. Có một mặt phẳng chứa a và b.

Khi đó, ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng có 3 khả năng xảy ra:

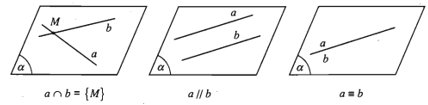
i) a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và kí hiệu $a\cap b=\left\{M\right\}$. Ta có thể viết $a\cap b=M$.

ii) a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.

iii) a trùng b, kí hiệu là $a\equiv b$.

- Trường hợp 2. Không có mặt phẳng nào chứa a và b.

Khi đó ta nói a và b chéo nhau hay a chéo với b.

- Ví dụ 1. Cho tứ diện ABCD. Hãy chỉ ra các cặp đường thẳng chéo nhau.

Lời giải:

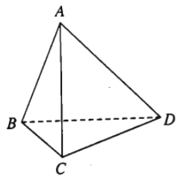
Đường thẳng AB và CD chéo nhau.

Đường thẳng AC và BD chéo nhau.

Đường thẳng AD và BC chéo nhau.

6. Tính chất về đường thẳng song song và đường thẳng chéo nhau trong không gian

- Định lí. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

- Định lí (về giao tuyến của ba mặt phẳng).

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

- Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

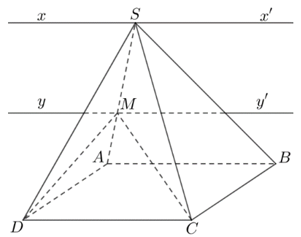
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng:

a) (SAD) và (SBC).

b) (MCD) và (SAB), với M là một điểm bất kì thuộc cạnh SA.

Lời giải:

 

 

 

 

 

 

 

 

 

 

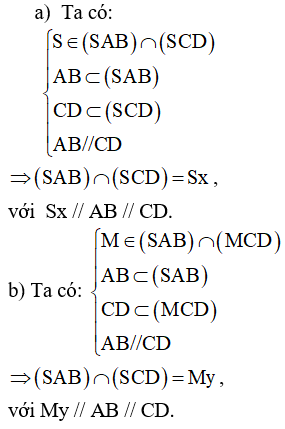
- Định lí. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

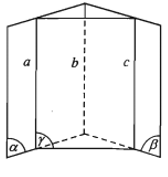
Ta có: a // c; b // c nên a // b hay a // b // c (ba đường thẳng song song).

 Ví dụ 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng IJ // AB, từ đó suy ra IJ // CD.

Lời giải:

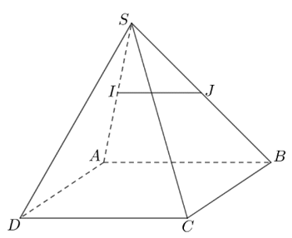
Xét tam giác SAB có I, J lần lượt là trung điểm của các cạnh SA, SB nên IJ là đường trung bình của tam giác SAB.

Từ đó suy ra IJ // AB.

Lại có AB // CD (vì ABCD là hình bình hành) nên từ đó ta có IJ // CD (vì cùng song song với đường thẳng AB).

7. Vị trí tương đối của đường thẳng và mặt phẳng

Cho đường thẳng d và mặt phẳng (α). Tùy theo số điểm chung của d và (α), ta có ba trường hợp sau:

- d và (α) không có điểm chung. Khi đó ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) // d.

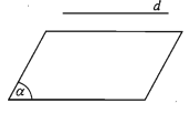
- d và (α) chỉ có một điểm chung duy nhất M. Khi đó ta nói d và (α) cắt nhau tại điểm M và kí hiệu $d\cap \left(\alpha \right)=M$.

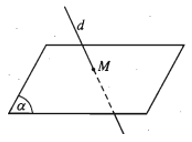
- d và (α) có từ hai điểm chung trở lên. Khi đó, d nằm trong (α) hay (α) chứa d và kí hiệu $d\subset \left(\alpha \right)$.

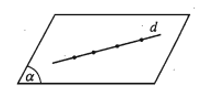
8. Tính chất về đường thẳng và mặt phẳng song song

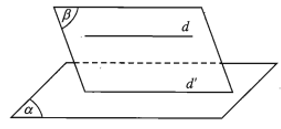
- Định lí. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).

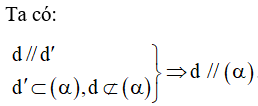
- Định lí. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với a.

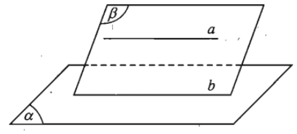
- Hệ quả. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

- Định lí. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Ví dụ 1. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O, O₁ lần lượt là tâm của ABCD và ABEF, gọi M là trung điểm của CD. Chứng minh:

a) OO₁ // mp (BEC).

b) OO₁ // mp (AFD)

Lời giải.

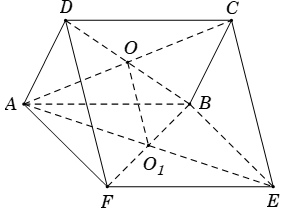
a)  Xét tam giác ACE có O; O₁ lần lượt là trung điểm của AC; AE (tính chất hình hình hành).

Suy ra OO₁ là đường trung bình trong tam giác ACE và OO₁ // EC.

Mà EC thuộc mp (BEC) nên OO₁ // mp (BEC)  (đpcm).

b) Tương tự; OO₁ là đường trung bình của tam giác BFD nên OO₁ // FD.

Mà FD nằm trong mp(AFD)

Suy ra: OO₁ // mp (AFD) (đpcm).

Ví dụ 2. Cho tứ diện ABCD. Gọi H là một điểm nằm trong tam giác ABC và (α)  là mặt phẳng đi qua H song song với AB và CD. Thiết diện của tứ diện cắt bởi mp (α) là hình gì?

Lời giải:

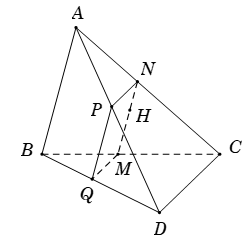
+ Qua H kẻ đường thẳng song song AB và đường thẳng này cắt BC, AC lần lượt tại M, N.

+ Từ N kẻ NP song song với CD $\left(P\in AD\right)$

 Từ P kẻ PQ song song với AB $\left(Q\in BD\right)$.

+ Ta có: MN // PQ // AB

Suy ra 4 điểm M; N; P và Q đồng phẳng .

Suy ra thiết diện của tứ diện cắt bởi mp (α) là tứ giác MNPQ.

+ Ta chứng minh MNPQ là hình bình hành.

Trước tiên, ta chứng minh  PN // QM.

Ta có:

$\left\{\begin{array}{c}PN\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}\hspace{0.17em}}CD\\ \begin{array}{l}PN\subset mp\left(MNPQ\right),\\ \hspace{0.17em}CD\subset mp\left(BCD\right)\\ QM=mp\left(MNPQ\right)\cap \\ mp\left(BCD\right)\end{array}\end{array}\right.$

Suy ra: QM // PN // CD

Lại có: PQ // MN

Do đó, tứ giác MNPQ là hình bình hành.

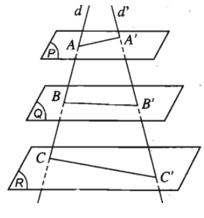
9. Định nghĩa hai mặt phẳng song song

Hai mặt phẳng (α), (β) được gọi là song song với nhau nếu chúng không có điểm chung.

Khi đó ta kí hiệu (α) // (β) hoặc (β) // (α).

10. Tính chất của hai mặt phẳng song song

- Định lí 1. Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) thì (α) song song với (β).

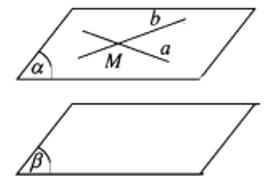
Ta có:

$$\begin{gathered} \left.\begin{array}{l}a,b\subset \left(\alpha \right),a\cap b=M\\ a\text{\hspace{0.17em}//\hspace{0.17em}}\left(\beta \right)\\ b\text{\hspace{0.17em}//\hspace{0.17em}}\left(\beta \right)\end{array}\right\} \\ \Rightarrow \left(\alpha \right)\text{//}\left(\beta \right) \end{gathered}$$

- Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

- Hệ quả 1. Nếu đường thẳng d song song với mặt phẳng (α) thì qua d có duy nhất một mặt phẳng song song với (α).

- Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

- Hệ quả 3. Cho điểm A không nằm trên mặt phẳng (α). Mọi đường thẳng đi qua A và song song với (α) đều nằm trong mặt phẳng đi qua A và song song với (α).

- Định lí 3. Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

$\left.\begin{array}{l}\left(\alpha \right)\text{//}\left(\beta \right)\\ a=\left(\alpha \right)\cap \left(\gamma \right)\\ b=\left(\beta \right)\cap \left(\gamma \right)\end{array}\right\}\Rightarrow a\text{\hspace{0.17em}//\hspace{0.17em}}b$

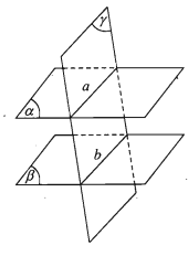
- Hệ quả. Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau

$$\begin{gathered} \left.\begin{array}{l}\left(\alpha \right)\text{//}\left(\beta \right)\\ a\cap \left(\alpha \right)=A,b\cap \left(\alpha \right)=A^{\text{'}}\\ a\cap \left(\beta \right)=B,b\cap \left(\beta \right)=B^{\text{'}}\\ A{A}^{\text{'}}=\left(\alpha \right)\cap \left(\gamma \right)\\ B{B}^{\text{'}}=\left(\beta \right)\cap \left(\gamma \right)\end{array}\right\} \\ \Rightarrow A{A}^{\text{'}}=B{B}^{\text{'}} \end{gathered}$$

Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Chứng minh:

a) M, N, O, P  đồng phẳng.

b) mp(MON) // mp(SBC).

Lời giải:

a) Ta có MN là đường trung bình của tam giác SAD nên MN // AD  (1).

Và OP là đường trung bình của tam giác ABC nên OP // BC // AD  (2).

Từ (1) và (2) suy ra MN // OP // AD nên 4 điểm M, N, O, P  đồng phẳng.

b) Vì $\left\{\begin{array}{c}MP\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}\hspace{0.17em}}SB\\ OP\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}}BC\\ \begin{array}{l}MP,OP\subset \left(MNOP\right)\\ SB,BC\subset \left(SBC\right)\end{array}\end{array}\right.$

Suy ra, (MNOP) // (SBC) hay (MON) // (SBC).

Ví dụ 2. Cho hình hộp ABCD.A’B’C’D’. Gọi I là trung điểm của A’B’. Mặt phẳng (IBD) cắt hình hộp theo thiết diện là hình gì?

Lời giải:

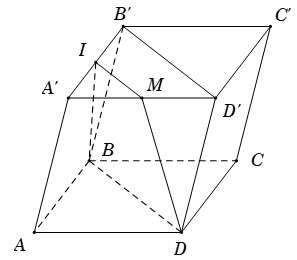
- Ta tìm giao tuyến của 2 mp(IBD) và (A’B’C’D’)

$\left\{\begin{array}{c}BD\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}B\text{'}D\text{'}\\ BD\subset \left(IBD\right);B\text{'}D\text{'}\subset (A\text{'}B\text{'}C\text{'}D\text{'})\\ Ichung\end{array}\right.$

Suy ra, giao tuyến của (IBD) với (A’B’C’D’) là đường thẳng d đi qua I và song song với BD.

- Trong mặt phẳng (A’B’C’D’), gọi M là giao điểm của d và A’D’.

Suy ra,  IM // BD // B’D’.

Khi đó thiết diện là tứ giác IMDB và tứ giác này là hình thang.

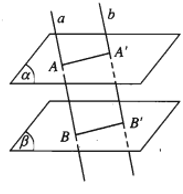
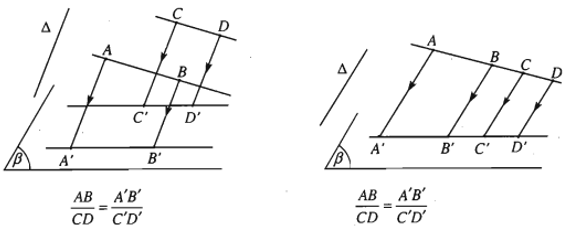
11. Định lí Ta – let (Thalès) trong không gian

- Định lí 4 (định lí Ta- let). Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

- Nếu d, d’ là hai cát tuyến bất kì cắt ba mặt phẳng song song (α), (β), lần lượt tại các điểm A, B, C và A’, B’, C’ thì:

$\frac{AB}{A\text{'}B\text{'}}=\frac{BC}{B\text{'}C\text{'}}=\frac{CA}{C\text{'}A\text{'}}$

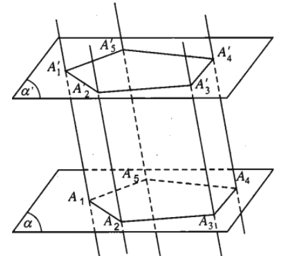
12. Hình lăng trụ, hình hộp

Cho hai mặt phẳng song song (α) và (α’). Trên (α) cho đa giác lồi A₁A₂…A_n. Qua các đỉnh A₁, A₂,.., A_n ta vẽ các đường thẳng song song với nhau và cắt (α’) lần lượt tại .

Hình gồm hai đa giác A₁A₂…A_n,  và các hình bình hành A₁A₁’A₂’A₂;

A₂A₂’A₃’A₃,…, A_nA_n’A₁’A₁ được gọi là hình lăng trụ và được kí hiệu là A₁A₂…A_n..

- Hai đa giác A₁A₂…A_n, gọi là hai mặt đáy của hình lăng trụ.

- Các đoạn thẳng A₁A’₁, A₂A₂’,…., A_nA_n’ gọi là các cạnh bên của hình lăng trụ.

- Các hình bình hành A₁A₁’A₂’A₂, A₂A₂’A₃’A₃, …, A_nA_n’A₁’A₁ được gọi là các mặt bên của hình lăng trụ.

- Các đỉnh của hai đa giác được gọi là các đỉnh của hình lăng trụ.

- Nhận xét:

+ Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.

+ Các mặt bên của hình lăng trụ là các hình bình hành.

+ Hai mặt đáy của hình lăng trụ là hai đa giác bằng nhau.

Người ta gọi tên của hình lăng trụ dựa vào tên của đa giác đáy, chẳng hạn:

+ Hình lăng trụ có đáy là hình tam giác được gọi là hình lăng trụ tam giác.

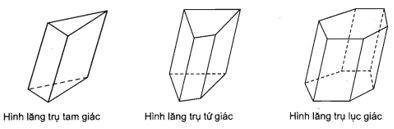
+ Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.

13. Hình chóp cụt

Định nghĩa:

Cho hình chóp S.A₁A₂…A_n ; một mặt phẳng (P) không qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh SA₁, SA₂, …,SA_n lần lượt tại A₁’; A₂’,.., A_n’. Hình tạo bởi thiết diện A₁’A₂’..A_n’ và đáy A₁A₂…A_n của hình chóp cùng với các tứ giác A₁A₁’A₂’A₂, A₂A₂’A₃’A₃,…, A_nA_n’A₁’A₁ gọi là hình chóp cụt.

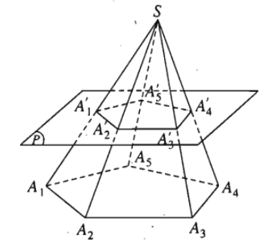
Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện A₁’A₂’..A_n’ gọi là đáy nhỏ của hình chóp cụt.

Các tứ giác A₁A₁’A₂’A₂, A₂A₂’A₃’A₃,…, A_nA_n’A₁’A₁ gọi là các mặt bên của hình chóp cụt.

Các đoạn thẳng A₁A’₁, A₂A₂’,…., A_nA_n’ gọi là các cạnh bên của hình chóp cụt.

- Tính chất của hình chóp cụt

(1) Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.

(2) Các mặt bên là những hình thang.

(3) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.

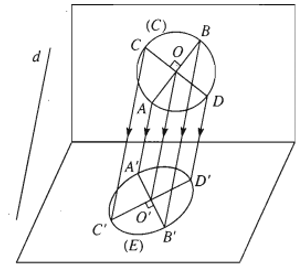
14. Phép chiếu song song

- Cho mặt phẳng (α) và đường thẳng ∆ cắt (α). Với mỗi điểm M trong không gian, đường thẳng đi qua M và song song hoặc trùng với ∆ sẽ cắt (α) tại điểm M’ xác định. Điểm M’ được gọi là hình chiếu song song của điểm M trên (α) theo phương ∆.

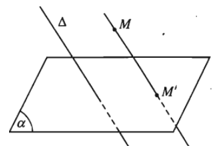
Mặt phẳng (α) gọi là mặt phẳng chiếu. Phương ∆ gọi là phương chiếu.

Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M’ của nó trên (α) được gọi là phép chiếu song song lên (α) theo phương ∆.

Nếu H là một hình nào đó thì tập hợp H’ các hình chiếu M’ của tất cả những điểm M thuộc H được gọi là hình chiếu của H qua phép chiếu song song nói trên.

- Chú ý. Nếu một đường thẳng có phương trùng với phương chiếu thì hình chiếu của đường thẳng đó là một điểm.

15. Các tính chất của phép chiếu song song

- Định lí 1.

a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

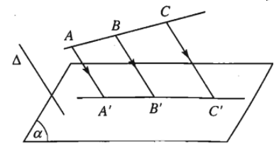
b) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

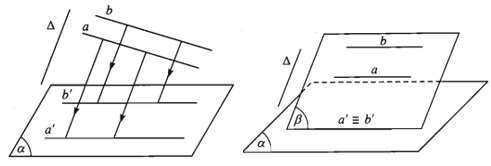
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

16. Hình biểu diễn của một hình không gian trên mặt phẳng.

Hình biểu diễn của hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.

- Hình biểu diễn của các hình thường gặp.

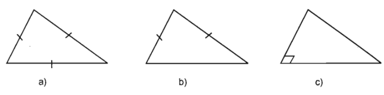
+ Tam giác: Một tam giác bất kì bao giờ cũng có thể coi là hình chiếu của một tam giác có dạng tùy ý cho trước (có  thể là tam giác đều, tam giác cân, tam giác vuông, …).

+ Hình bình hành: Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuoongm hình thoi, hình chữ nhật, …).

+ Hình thang: Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tùy ý cho trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.

+ Hình tròn: Người ta thường dùng hình elip để biểu diễn hình tròn.

Xem thêm:

Đề thi Toán lớp 11 học kì 1 năm 2022 - 2023 có đáp án

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng học kì 1

Năm học 2022 - 2023

Môn: Toán 11

Thời gian làm bài: 45 phút

Đề thi Toán lớp 11 học kì 1 năm 2022 - 2023 có đáp án Đề số 1

Thời gian: 90 phút   

Câu 1: Phương trình: $2{\sin }^{2}x+\sin x.\cos x-{\cos }^{2}x=1$ có các nghiệm là

A. $\mathrm{x}=\arctan (-\frac{1}{2})+k\mathrm{\pi }; \mathrm{x}=\frac{\mathrm{\pi }}{2}+\mathrm{k\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

B. $\mathrm{x}=\arctan (-2)+k\mathrm{\pi }; \mathrm{x}=\frac{\mathrm{\pi }}{4}+\mathrm{k\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

C. $\mathrm{x}=\arctan 2+k\mathrm{\pi }; \mathrm{x}=\frac{\mathrm{\pi }}{4}+\mathrm{k\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

D. $\mathrm{x}=\arctan 2+k\mathrm{\pi }; \mathrm{x}=\frac{\mathrm{\pi }}{3}+\mathrm{k\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

Lời giải

Ta thấy cosx = 0 không thỏa mãn phương trình đã cho

$\Rightarrow$ Chia cả 2 vế của phương trình cho cos²x ta được:

$\begin{array}{l}2{\tan }^{2}x+\tan x-1={\tan }^{2}x+1\iff {\tan }^{2}x+\tan x-2=0\\ \iff \left[\begin{array}{c}\tan x=1\\ \tan x=-2\end{array}\right.\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\arctan \left(-2\right)+k\pi \end{array}\right.\end{array}$

Chọn B.

Câu 2: Số nghiệm của phương trình $\sqrt{3}\sin 3x+\cos 3x=\sqrt{2}$ trong khoảng $(-\mathrm{\pi };\mathrm{\pi })$ là

A. 5

B. 7

C. 4 

D. 6

Lời giải

Ta có: $\sqrt{3}\sin 3x+\cos 3x=\sqrt{2}$

$\begin{array}{l}\iff \frac{\sqrt{3}}{2}\sin 3x+\frac{1}{2}\cos 3x=\frac{\sqrt{2}}{2}\\ \iff c\text{os}\frac{\pi }{6}.\sin 3x+\text{\hspace{0.17em}\hspace{0.17em}}\sin \frac{\pi }{6}.c\text{os 3x = \hspace{0.17em}}\frac{\sqrt{2}}{2}\iff \sin \left(3x+\frac{\pi }{6}\right)=\frac{\sqrt{2}}{2}\end{array}$

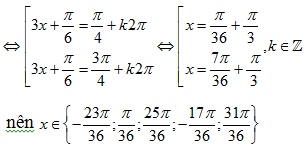
Chọn A.

Câu 3: Phương trình ${\cos }^{2}x+{\cos }^{2}2x+{\cos }^{2}3x+{\cos }^{2}4x=2$ tương đương với phương trình

A. $\cos x.\cos 2x.\cos 5x=0$

B. $\sin x.\sin 2x.\sin 4x=0$

C. $\sin x.\sin 2x.\sin 5x=0$

D. $\cos x.\cos 2x.\cos 4x=0$

Lời giải

Phương trình đã cho $\iff (2{\cos }^{2}x-1)+(2{\cos }^{2}2x-1)+(2{\cos }^{2}3x-1)+(2{\cos }^{2}4x-1)=0$

$\iff \cos 2x+\cos 4x+\cos 6x+\cos 8x=0$

$\iff 2\cos 3x.\cos x+2\cos 7x.\cos x=0$

$\iff \cos x(\cos 3x+\cos 7x)=0$

$\iff \cos x.2\cos 5x.\cos 2x=0$

$\iff \cos x.\cos 5x.\cos 2x=0$

Chọn A.

Câu 4: Cho đa giác đều n đỉnh, $n\in N$ và $n\ge 3$. Tìm n biết rằng đa giác đã cho có 135 đường chéo.

A. n = 15

B. n = 27

C. n = 8

D. n = 18

Lời giải.

Đa giác lồi n đỉnh thì có n cạnh. Nếu vẽ tất cả các đoạn thẳng nối từng cặp trong n đỉnh này thì có một bộ gồm các cạnh và các đường chéo. 

Vậy để tính số đường chéo thì lấy tổng số đoạn thẳng dựng được trừ đi số cạnh, với:

- Tất cả đoạn thẳng dựng được là bằng cách lấy ra 2 điểm bất kỳ trong n điểm, tức là số đoạn thẳng chính là số tổ hợp chập 2 của n phần tử.

Như vậy, tổng số đoạn thẳng là $C_n^2$

- Số cạnh của đa giác lồi là n

Suy ra số đường chéo của đa giác đều n đỉnh là $C_n^2-n=\frac{n(n-3)\text{}}{2}$

Theo bài ra, ta có $\frac{n(n-3)\text{}}{2}=135$

$\iff n^2-3n=270\iff n=18(\text{}vin>3)$

Chọn D.

Câu 5: Phương trình nào sau đây vô nghiệm

A. $\sin x=\frac{2}{3}$

B. $2\sin x-3\cos x=4$

C. $\tan x=2017$

D. $\sin 2x=\frac{1}{3}$

Lời giải

Các phương trình ở các đáp án A, C và D có nghiệm.

Xét phương trình: $2\sin x-3\cos x=4$

Vì 4² < 2² + (-3)² nên phương trình vô nghiệm

Chọn B.

Câu 6: Cho đường tròn (C): (x + 2)² + (y - 1)²=9. Ảnh của đường tròn (C) qua phép Đ_O là đường tròn có phương trình nào dưới đây?

A. ${(x + 1)}^2 + {(y - 2)}^2=9$

B. ${(x - 2)}^2 + {(y +1)}^2=9$

C. ${(x + 2)}^2 + {(y +1)}^2=9$

D. ${(x -2)}^2 + {(y - 1)}^2=9$

Lời giải

Đường tròn (C) có tâm I($-$2; 1) và bán kính R = 3

D₀(I) = I'(2; $-$1).

Gọi (C') là ảnh của (C) qua phép D₀$\Rightarrow$(C') tâm I'(2; -1) và bán kính R’ = R = 3 .

Khi đó (C'): ${(x-2)}^2+{(y+1)}^2=9$

Chọn B.

Câu 7: Gieo một con xúc sắc cân đối đồng chất hai lần. Tính xác suất sao cho tổng số chấm của hai lần gieo là số lẻ

A. $P=\frac{1}{2}$

B. $P=\frac{3}{5}$

C. $P=\frac{3}{7}$

D. $P=\frac{5}{9}$

Lời giải

Số phần tử của không gian mẫu là:  (phần tử)

Để tổng số chấm lẻ thì số cách chọn là: 6.3 = 18 (cách)

Xác suất để tổng số chấm của hai lần gieo là số lẻ là: $P=\frac{18}{36}=\frac{1}{2}$

Chọn A.

Câu 8: Tập nghiệm của phương trình $(x-3)(\sqrt{4-x^2}-x)=0$

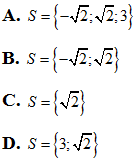
Lời giải

Điều kiện: $4-x^2\ge 0\iff -2\le x\le 2$ (*)

Với điều kiện (*) phương trình đã cho

$\iff \left[\begin{array}{l}x-3=0\\ \sqrt{4-x^2}-x=0\end{array}\right.\iff \left[\begin{array}{l}x=3\\ \sqrt{4-x^2}=x\end{array}\right.\iff \left[\begin{array}{l}x=3\\ \left\{\begin{array}{l}x\ge 0\\ 4-x^2=x^2\end{array}\right.\end{array}\right.$

$\iff \left[\begin{array}{l}x=3\\ \left\{\begin{array}{l}x\ge 0\\ x=\pm \sqrt{2}\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}x=3\\ x=\sqrt{2}\end{array}\right.\Rightarrow S=\left\{3;\sqrt{2}\right\}$

Chọn D.

Câu 9: Điều kiện xác định của hàm số $y=\frac{1}{sinx-\cos x}$ là

A. $x\ne \frac{\mathrm{\pi }}{2}+k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

B. $x\ne k2\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

C. $x\ne \frac{\mathrm{\pi }}{4}+k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

D. $x\ne k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

Lời giải

Điều kiện: $\sin x-\cos x\ne 0$

$\begin{array}{l}\iff \sqrt{2}\sin \left(x-\frac{\pi }{4}\right)\ne 0\iff x-\frac{\pi }{4}\ne k\pi \\ \iff x\ne \frac{\pi }{4}+k\pi ,k\in \mathbb{Z}\end{array}$

Chọn C.

Câu 10: Trong các khẳng định sau, khẳng định nào sai

 

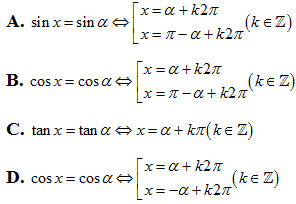
Lời giải

Chọn B.

Câu 11: Tập xác định của hàm số $y=cot(x+\frac{\mathrm{\pi }}{3})$ là

A. $\mathrm{ℝ} \backslash \left\{-\frac{\mathrm{\pi }}{3}+k2\mathrm{\pi }; \mathrm{k}\in \mathrm{\mathbb{Z}}\right\}$

B. $\mathrm{ℝ} \backslash \left\{-\frac{\mathrm{\pi }}{3}+k\mathrm{\pi }; \mathrm{k}\in \mathrm{\mathbb{Z}}\right\}$

C. $\mathrm{ℝ} \backslash \left\{\frac{\mathrm{\pi }}{6}+k2\mathrm{\pi }; \mathrm{k}\in \mathrm{\mathbb{Z}}\right\}$

D. $\mathrm{ℝ} \backslash \left\{\frac{\mathrm{\pi }}{6}+k\mathrm{\pi }; \mathrm{k}\in \mathrm{\mathbb{Z}}\right\}$

Lời giải

Điều kiện $\sin \left(x+\frac{\pi }{3}\right)\ne 0\iff x+\frac{\pi }{3}\ne k\pi \iff x\ne -\frac{\pi }{3}+k\pi$

TXĐ: $D=ℝ\backslash \left\{-\frac{\pi }{3}+k\pi ;k\in \mathbb{Z}\right\}$

Chọn B.

Câu 12: Giải phương trình $4({\sin }^{4}x+{\cos }^{4}x)+\sqrt{3}\sin 4x=2$

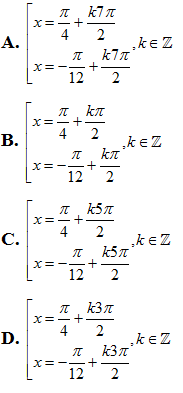
Lời giải

Phương trình đã cho $\iff 4\left[{\left({\sin }^{2}x+{\cos }^{2}x\right)}^2-2{\sin }^{2}x{\cos }^{2}x\right]+\sqrt{3}\sin 4x=2$

$\iff 4\left(1-\frac{{\sin }^{2}2x}{2}\right)+\sqrt{3}\sin 4x=2\iff \sqrt{3}\sin 4x+\cos 4x=-1\iff \frac{\sqrt{3}}{2}\sin 4x+\frac{1}{2}\cos 4x=-\frac{1}{2}$

$\iff \sin \left(4x+\frac{\pi }{6}\right)=-\frac{1}{2}\iff \left[\begin{array}{l}4x+\frac{\pi }{6}=-\frac{\pi }{6}+k2\pi \\ 4x+\frac{\pi }{6}=\frac{7\pi }{6}+k2\pi \end{array}\right.\iff \left[\begin{array}{l}x=-\frac{\pi }{12}+\frac{k\pi }{2}\\ x=\frac{\pi }{4}+\frac{k\pi }{2}\end{array}\right.,k\in \mathbb{Z}$

Chọn B.

Câu 13: Lớp 11A7 có 18 nam và 24 nữ. Chọn ngẫu nhiên hai học sinh để hát song ca. Xác suất để trong đó có ít nhất một nam là?

A. $\frac{236}{287}$

B. $\frac{195}{287}$

C. $\frac{92}{287}$

D. $\frac{51}{287}$

Lời giải

Số cách chọn ngẫu nhiên 2 học sinh là: $C_{42}^2=861$ (Cách)

Số cách chọn 2 học sinh để có ít nhất 1 nam là: $18.24+C_{18}^2=585$ (Cách)

Xác suất để có ít nhất 1 nam là: $\frac{585}{861}=\frac{195}{287}$

Chọn B.

Câu 14: Giá trị nhỏ nhất của $y=4-3\cos 2x$ là

A. 1

B. 7

C. -7

D. -3

Lời giải

Ta có: $\cos 2x\le 1\Rightarrow -3\cos 2x\ge -3\Rightarrow y=4-3\cos 2x\ge 4-3=1$

Vậy GTNN của y = 1 khi $\cos 2x=1\iff 2x=k2\pi \iff x=k\pi$

Chọn A.

Câu 15: Cho tập $A=\left\{0; 1; 2; 3; 4; 5; 6; 7\right\}$. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có bốn chữ số đôi một khác nhau?

A. 2048

B. 420

C. 840

D. 750

Lời giải

Gọi số tự nhiên có 4 chữ số thỏa mãn đề bài là $\overline{abcd}$

+) Nếu d = 0 thì số cách chọn abc là: $A_7^3=210$ (cách)

+) Nếu $d\in \left\{2;4;6\right\}$ thì a có 6 cách chọn $\Rightarrow$ số cách chọn là bc là $A_6^2$

Trong trường hợp này có: $\mathrm{3.6.}{A}_6^2=540$ (cách)

Số các số thỏa mã đề bài là:: $210+540=750$ (số)

Chọn D.

Câu 16: Cho đường thẳng $\left(d\right): \left\{\begin{array}{l}x=2+t\\ y=3+2t\end{array}\right., (t\in \mathrm{ℝ})$. Điểm nào sau đây thuộc đường thẳng (d):

A. (-1; 5)

B. (-2; -3)

C. (2; 3)

D. (-3; -1)

Lời giải

Thay x = -1 điểm

Chọn A.

Câu 17: Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực nhật sao cho có ít nhất 2 nữ?

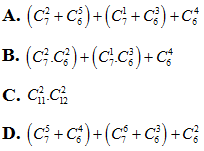
Lời giải

Có các cách chọn sau:

+) 2 nữ, 2 nam $\Rightarrow C_6^2{C}_7^2$ (cách)

+) 3 nữ, 1 nam $\Rightarrow C_6^3{C}_7^1$ (cách)

+) 4 nữ $\Rightarrow C_6^4$ (cách)

Theo quy tắc cộng, số cách chọn là: $\left(C_6^2{C}_7^2\right)+\left(C_6^3{C}_7^1\right)+C_6^4$ (cách)

Chọn B.

Câu 18: Phương trình $2\cos x+1=0$ có nghiệm là

A. $x=\pm \frac{2\mathrm{\pi }}{3}+k2\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

B. $x=\pm \frac{2\mathrm{\pi }}{3}+k\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

C. $x=\pm \frac{\mathrm{\pi }}{3}+k2\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

D. $x=\frac{\mathrm{\pi }}{3}+k2\mathrm{\pi }, \frac{2\mathrm{\pi }}{3}+\mathrm{k}2\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

Lời giải

 Phương trình đã cho $\iff \cos x=-\frac{1}{2}\iff x=\pm \frac{2\mathrm{\pi }}{3}+k2\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

Chọn A.

Câu 19: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Phép đối xứng trục là phép đồng nhất

B. Thực hiện liên tiếp phép quay và phép vị tự ta được phép đồng dạng.

C. Phép đồng dạng là một phép dời hình.

D. Phép vị tự là một phép dời hình.

Lời giải

Chọn B.

Câu 20: Cho 2 đường thẳng song song. Trên đường thẳng thứ nhất lấy 7 điểm phân biệt, trên đường thẳng thứ hai lấy 9 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh thuộc tập 16 điểm đã lấy trên hai đường thẳng trên?

A. 560 tam giác

B. 270 tam giác

C. 441 tam giác

D. 150 tam giác

Lời giải

TH1. Lấy 2 điểm thuộc d₁; 1 điểm thuộc d₂ có $C_7^2.C_9^1$ tam giác

TH2. Lấy 1 điểm thuộc d₂; 2 điểm thuộc d₁ có $C_7^1.C_9^2$ tam giác

Vậy số tam giác cần tìm là $C_7^2.C_9^1+C_7^1.C_9^2=441$

Chọn C.

Câu 21: Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen, lấy ngẫu nhiên đồng thời hai quả. Tính xác suất để hai quả đó cùng màu

A. $\frac{3}{5}$

B. $\frac{1}{5}$

C. $\frac{3}{10}$

D. $\frac{2}{5}$

Lấy ngẫu nhiên 2 quả cầu trong 5 quả cầu có $C_5^2$ cách

TH1. 2 quả cầu lấy ra cùng màu trắng $\Rightarrow$có $C_3^2$ cách

TH1. 2 quả cầu lấy ra cùng màu đen $\Rightarrow$ có $C_2^2$ cách

Vậy xác suất cần tính là $P=\frac{C_3^2+C_2^2}{C_5^2}=\frac{2}{5}$

Chọn D.

Câu 22: Giá trị nhỏ nhất của hàm số $y=2-\sin x-cox$ là

A. $2+\sqrt{2}$

B. $-2+\sqrt{2}$

C. $2-\sqrt{2}$

D. $-2-\sqrt{2}$

Lời giải

Ta có $\sin x+\cos x=\sqrt{2}\sin \left(x+\frac{\pi }{4}\right)$

Mà $-1\le \sin \left(x+\frac{\pi }{4}\right)\le 1;\forall x\in ℝ\Rightarrow -\sqrt{2}\le \sin x+\cos x\le \sqrt{2}$

Khi đó $2-\sqrt{2}\le 2-\left(\sin x+\cos x\right)\le 2+\sqrt{2}\iff 2-\sqrt{2}\le y\le 2+\sqrt{2}$

Chọn C.

Câu 23: Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi A là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và B là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố $A\cup B$

A. $A\cup B=\left\{SSS, SSN, NSS, SNS, NNN\right\}$

B. $A\cup B=\left\{SSS, NNN\right\}$

C. $A\cup B=\left\{SSS, SSN, NSS, NNN\right\}$

D. $A\cup B=\Omega$

Lời giải

Phần tử của biến cố B là $B=\left\{SSS, NNN\right\}$

Phần tử của biến cố A là $A=\left\{SSS, SSN, NSS\right\}$

Vậy $A\cup B=\left\{SSS,SSN,NSS,NNN\right\}$

Chọn C

Câu 24: Trong mp Oxy cho $\overrightarrow{v}=(2; 1)$ và điểm A(1; 3). Tìm ảnh của A qua phép $T_{\overrightarrow{v}}$?

A. $(-1; 2)$

B. $(-1; -2)$

C. $(1;- 2)$

D. $(3; 4)$

Lời giải

Ta có $T_{\overrightarrow{v}}\left(A\right)=A\text{'}\Rightarrow \overrightarrow{AA\text{'}}=\overrightarrow{v}=(2; 1)\Rightarrow \left\{\begin{array}{l}{x}_{A\text{'}}-1=2\\ y_{A\text{'}}-3=1\end{array}\right.\Rightarrow A\text{'}(3; 4)$

Chọn D.

Câu 25: Có hai chiếc hộp: Hộp thứ nhất chứa bốn bi xanh, ba bi vàng; Hộp thứ hai chứa hai bi xanh, một bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Xác suất để được hai bi xanh là;

A. $\frac{3}{5}$

B. $\frac{26}{21}$

C. $\frac{8}{21}$

D. $\frac{4}{7}$

Lời giải

Lấy 1 bi từ hộp thứ nhất có 7 cách, 1 bi từ hộp thứ hai có 3 cách $\Rightarrow n\left(\Omega \right)=7.3=21$

Lấy 1 bi xanh từ hộp thứ nhất có 4 cách, 1 bi xanh từ hộp thứ hai có 2 cách $\Rightarrow n\left(X\right)=4.2=8$

Vậy xác suất cần tính là $P=\frac{n\left(X\right)}{n\left(\Omega \right)}=\frac{8}{21}$

Chọn C.

Câu 26: Biết n là số nguyên dương thỏa mãn $C_{n+1}^3-A_n^2=14\left(n-1\right)$. Giá trị của n là:

A. 15

B. 16

C. 14

D. 12

Lời giải

Phương trình $C_{n+1}^3-A_n^2=14\left(n-1\right)\iff \frac{\left(n+1\right)!}{\left(n-2\right)!.3!}-\frac{n!}{\left(n-2\right)!}=14\left(n-1\right)$

$\begin{array}{l}\iff \frac{n\left(n+1\right)\left(n-1\right)}{6}-n\left(n-1\right)=14\left(n-1\right)\iff \frac{n\left(n+1\right)}{6}-n=14\\ \iff n\left(n+1\right)-6n=84\iff n^2-5n-84=0\iff n=12\end{array}$

Chọn D.

Câu 27: Trong mặt phẳng, với hệ tọa độ Oxy, cho điểm M(1; -3). Phép tịnh tiến theo véctơ $\overrightarrow{v}=(2; 4)$ biến M thành điểm

A. M' (1; 7)

B. M' (3; 2)

C. M' (3; 1)

D. M' (-1; -7)

Lời giải

Ta có $T_{\overrightarrow{v}}\left(M\right)=M\text{'}\stackrel{}{\to }\overrightarrow{MM\text{'}}=\overrightarrow{v}\Rightarrow \left\{\begin{array}{l}{x}_{M\text{'}}-1=2\\ y_{M\text{'}}+3=4\end{array}\right.\Rightarrow \left\{\begin{array}{l}{x}_{M\text{'}}=3\\ y_{M\text{'}}=1\end{array}\right.$

Vậy $M\text{'} \left(3; 1\right)$

Chọn C.

Câu 28: Trong mp Oxy cho đường thẳng d có phương trình $3x+y-3=0$. Ảnh của đường thẳng d qua phép $V_{\left(O;-2\right)}$ biến đường thẳng d thành đường thẳng có phương trình là:

A. $-3x-y+3=0$

B. $3x+y+6=0$

C. $3x+y-6=0$

D. $3x+y-3=0$

Lời giải

Gọi d’ là ảnh của d qua phép $V_{\left(O;-2\right)}\Rightarrow$phương trình $\left(d\text{'}\right):3x+y+m=0$

Gọi $A\left(1;0\right)\in \left(d\right)$ và $V_{\left(O;-2\right)}\left(A\right)=A\text{'}\Rightarrow \overrightarrow{OA\text{'}}=-2\overrightarrow{OA}=\left(-2;0\right)\Rightarrow A\text{'}\left(-2;0\right)$

Mặt khác $A\text{'}\in \left(d\text{'}\right)$ suy ra $3.\left(-2\right)+0+m=0\iff m=6$

Vậy $\left(d\text{'}\right):3x+y+6=0$

Chọn B.

Câu 29: Lớp 11A7 có 18 học sinh nam và 24 học sinh nữ. Thầy chủ nhiệm cần chọn 10 học sinh để luyện tập vũ khúc sân trường. Hỏi thầy chủ nhiệm có bao nhiêu cách chọn 10 học sinh sao cho có ít nhất 1 học sinh nữ?

A. $C_{18}^{10}$

B. $C_{42}^{10}-C_{18}^{10}$

C. $C_{42}^{10}-C_{24}^{10}$

D. $C_{24}^{10}$

Lời giải

Lớp học có tất cả 42 học sinh

Số cách chọn 10 học sinh từ 42 học sinh là $C_{42}^{10}$

Giả sử trong 10 học sinh được chọn không có học sinh nữ có $C_{18}^{10}$ cách chọn

Vậy số cách chọn thỏa mãn yêu cầu bài toán là $C_{42}^{10}-C_{18}^{10}$

Chọn B.

Câu 30: Hàm số $y=\sin 2x-\tan 2x$ tuần hoàn với chu kỳ là bao nhiêu?

A. $T=3\mathrm{\pi }$

B. $T=\frac{\mathrm{\pi }}{2}$

C. $T=2\mathrm{\pi }$

D. $T=\mathrm{\pi }$

Lời giải

Hàm số y = sin 2x tuần hoàn với chu kì $T_1=\frac{2\mathrm{\pi }}{2}=\mathrm{\pi }$

Hàm số y = tan2x tuần hoàn với chu kì $T_2=\frac{\pi }{2}$

Do đó; hàm số đã cho tuần hoàn với chu kì $T=\mathrm{\pi }$

Chọn D.

Câu 31: Giải phương trình $cot(4x-{20}^0)=\frac{1}{\sqrt{3}}$

A. $x={35}^0+k{90}^0, k\in \mathrm{\mathbb{Z}}$

B. $x={20}^0+k{90}^0, k\in \mathrm{\mathbb{Z}}$

C. $x={20}^0+k{45}^0, k\in \mathrm{\mathbb{Z}}$

D. $x={30}^0+k{45}^0, k\in \mathrm{\mathbb{Z}}$

Lời giải

Ta có

$\begin{array}{l}\cot \left(4x-{20}^0\right)=\frac{1}{\sqrt{3}}\iff \cot \left(4x-{20}^0\right)=\cot {60}^0\\ \iff 4x-{20}^0={60}^0+k{.180}^0\\ \iff x={20}^0+k{.45}^0\end{array}$

Chọn C.

Câu 32: Sắp xếp 5 người trong đó có An và Linh ngồi vào 5 ghế thẳng hàng. Xác suất để An và Linh không ngồi cạnh nhau là:

A. $\frac{1}{5}$

B. $\frac{4}{5}$

C. $\frac{2}{5}$

D. $\frac{3}{5}$

Lời giải

Sắp xếp 5 người vào 5 ghế có 5!=120 cách

Giả sử An và Linh ngồi cạnh nhau, khi đó coi An và Linh là một phần tử  + 3 người còn lại ngồi vào ghế.

Khi đó, có $2! x 4! = 48$ cách sắp xếp để An và Linh ngồi cạnh nhau

Vậy có 120 - 48 = 72 cách sắp xếp để An và Linh không ngồi cạnh nhau

$\Rightarrow P=\frac{72}{120}=\frac{3}{5}$

Chọn D.

Câu 33: Từ thành phố A tới thành phố B có 4 con đường, từ thành phố B tới thành phố C có 5 con đường. Hỏi có bao nhiêu cách đi từ A tới C qua B chỉ một lần.

A. 9

B. 20

C. 1

D. 25

Lời giải

Đi từ $A\to B$ có 4 cách, đi từ $B\to C$ có 5 cách.

Theo quy tắc nhân, đi từ $A\to C$ có $4 x 5 = 20$ cách

Chọn B.

Câu 34: Phương trình ${\sin }^{2}x- 3\sin x + 2 = 0$

A. $x = \frac{\mathrm{\pi }}{2}+k2\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

B. $x = k\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

C. $x = -\frac{\mathrm{\pi }}{2}+k2\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

D. $x = k2\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$

Lời giải

Phương trình ${\sin }^{2}x-3\sin x+2=0\iff \left(\sin x-1\right)\left(\sin x-2\right)=0$

$\iff \left[\begin{array}{l}\sin x=1\\ \sin x=2\end{array}\right.\iff \sin x=1\iff x=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

Chọn A.

Câu 35: Trong mặt phẳng Oxy cho đường thẳng d có phương trình: $x-2y+3=0$. Ảnh của đường thẳng d qua phép tịnh tiến theo véctơ $\overrightarrow{v}=(2; -1)$ có phương trình:

A. $x-2y+1=0$

B. $x-2y+3=0$

C. $2x-4y+3=0$

D. $x-2y-1=0$

Lời giải

Gọi d’ là ảnh của d qua phép $T_{\overrightarrow{v}}\Rightarrow$ phương trình $\left(d\text{'}\right):x-2y+m=0$. Gọi $A\left(1;2\right)\in \left(d\right)$ và $T_{\overrightarrow{v}}\left(A\right)=A\text{'}\Rightarrow \overrightarrow{AA\text{'}}=\overrightarrow{v}=\left(2;-1\right)\Rightarrow A\text{'}\left(3;1\right)$.

Mặt khác $A\text{'}\in \left(d\text{'}\right)$ suy ra $3-2.1+m=0\iff m=-1$.

Vậy $\left(d\text{'}\right):x-2y-1=0$.

Chọn D.

Câu 36: Phép vị tự tâm O(0; 0) tỉ số -2 biến đường tròn: ${(x-1)}^2+{(y-2)}^2=4$ thành:

A. ${(x-1)}^2+{(y-4)}^2=16$

B. ${(x-4)}^2+{(y-2)}^2=4$

C. ${(x-1)}^2+{(y-2)}^2=16$

D. ${(x-2)}^2+{(y+4)}^2=16$

Lời giải

Xét đường tròn $\left(C\right):{\left(x-1\right)}^2+{\left(y-2\right)}^2=4$, có tâm $I\left(1; 2\right)$ bán kính R = 2

Gọi (C') là ảnh của (C) qua phép $V_{\left(O;-2\right)}\Rightarrow R\text{'}=\left|-2\right|.R=4$

Gọi $I\text{'}\left(x_0;y_0\right)$ là tâm đường tròn (C'), ta có $V_{\left(O;-2\right)}\left(I\right)=I\text{'}\Rightarrow \overrightarrow{OI\text{'}}=-2\overrightarrow{OI}=\left(-2;-4\right)$.

$\Rightarrow I\text{'}\left(-2;-4\right)$. Vậy phương trình đường tròn $\left(C\text{'}\right)$ là ${\left(x+2\right)}^2+{\left(y+4\right)}^2=16$.

Chọn D.

Câu 37: Phương trình $\sin x+\cos x=\sqrt{2}\sin 5x$

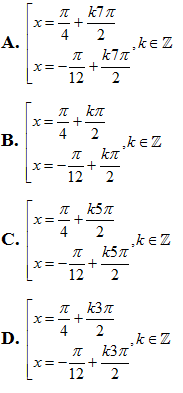
Lời giải

Phương trình $\sin x+\cos x=\sqrt{2}\sin 5x$

$\iff \sqrt{2}\sin \left(x+\frac{\pi }{4}\right)=\sqrt{2}\sin 5x\iff \sin \left(x+\frac{\pi }{4}\right)=\sin 5x$

$\iff \left[\begin{array}{l}x+\frac{\pi }{4}=5x+k2\pi \\ x+\frac{\pi }{4}=\pi -5x+k2\pi \end{array}\right.\iff \left[\begin{array}{l}4x=\frac{\pi }{4}-k2\pi \\ 6x=\frac{3\pi }{4}+k2\pi \end{array}\right.\iff \left[\begin{array}{l}x=\frac{\pi }{16}-k\frac{\pi }{2}\\ x=\frac{\pi }{8}+k\frac{\pi }{3}\end{array}\right.$

Chọn A.

Câu 38: Để chào mừng ngày 26/3 Đoàn trường THPT XXX tổ chức giải bóng đá có 10 đội tham dự theo thể thức thi đấu vòng tròn tính điểm (hai đội bất kỳ đều gặp nhau đúng 1 trận). Hỏi đoàn trường phải tổ chức bao nhiêu trận đấu ?

A. 10 trận

B. 45 trận

C. 90 trận 

D. Kết quả khác

Lời giải

Cứ 2 đội ta sẽ có 1 trận bóng đá

Với 10 đội, đoàn trưởng phải tổ chức số trận là $C_{10}^2=45$

Chọn B.

Câu 39: Đường thẳng đi qua điểm A(-2; -1) và song song với đường thẳng y = 2x -1 có phương trình là

A. $y=-2x+5$

B. $y=2x-6$

C. $y=2x+5$

D. $y=-2x-5$

Lời giải

Gọi phương trình đường thẳng cần tìm là $\left(d\right):y=ax+b$

Vì $\left(d\right)\text{//}y=2x-3\Rightarrow \left\{\begin{array}{l}a=2\\ b\ne -3\end{array}\right.$

Mà (d) đi qua $A\left(-2;1\right)\Rightarrow -2a+b=1\iff b=5$

Vậy phương trình đường thẳng $\left(d\right):y=2x+5$

Chọn C.

Câu 40: Cho tập $A=\left\{0; 1; 2; 3; 4; 5; 6; 7; 8; 9\right\}$. Số các số tự nhiên có năm chữ số đôi một khác nhau được lấy ra từ tập A là

A. 30420

B. 27216

C. 15120

D. 27162

Lời giải

Gọi số cần tìm có dạng $\overline{abcde}$ với $a, b, c, d \in A$

Suy ra a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 7 cách chọn, e có 6 cách chọn.

Khi đó, có tất cả 9.9.8.7.6 = 27216 số cần tìm

Chọn B.

Câu 41: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 3y +1 = 0. Để phép tịnh tiến theo vector $\overrightarrow{v}$ biến đường thẳng d thành chính nó thì $\overrightarrow{v}$ phải là vecto nào trong số các vecto sau ?

A. $\overrightarrow{v}=(3; 2)$

B. $\overrightarrow{v}=(-2;-3)$

C. $\overrightarrow{v}=(2;-3)$

D. $\overrightarrow{v}=(3;- 2)$

Lời giải

Giả sử vector $\overrightarrow{v}=(a; b)$

Gọi M(x; y) là điểm thuộc đường thẳng d và M'(x'; y') là ảnh của đường thẳng d qua phép tịnh tiến vector $\overrightarrow{v}$

Ta có $T_{\overrightarrow{v}}\left(M\right)=M\text{'}\Rightarrow \left\{\begin{array}{l}x\text{'}=x+a\\ y\text{'}=y+b\end{array}\right.\iff \left\{\begin{array}{l}x=x\text{'}-a\\ y=y\text{'}-b\end{array}\right.$

Mà $M\in d\Rightarrow 2\left(x\text{'}-a\right)-3\left(y\text{'}-b\right)+1=0\iff 2x\text{'}-3y\text{'}-2a+3b+1=0$

Mà $T_{\overrightarrow{v}}\left(d\right)=d\Rightarrow -2a+3b+1=0\iff 2a=3b$

nên $\overrightarrow{v}(3; 2)$ thỏa mãn 

Chọn A.

Câu 42: Một thùng có 7 sản phẩm, trong đó có 4 sản phầm loại I và 3 sản phầm loại II. Lấy ngẫu nhiên 2 sản phẩm. Xác suất để lấy được 2 sản phẩm cùng loại là

A. $\frac{1}{7}$

B. $\frac{3}{7}$

C. $\frac{4}{7}$

D. $\frac{2}{7}$

Lời giải

Không gian mẫu là $\left|\Omega \right|=C_7^2$

Số phần tử thuận lợi cho biến cố là $\left|{\Omega }_A\right|=C_4^2+C_3^2\Rightarrow P_A=\frac{\left|{\Omega }_A\right|}{\left|\Omega \right|}=\frac{C_4^2+C_3^2}{C_7^2}=\frac{3}{7}$

Chọn B.

Câu 43: Số hạng không chứa x trong khai triển ${\left(x^2+\text{\hspace{0.17em}\hspace{0.17em}}\frac{2}{x^2}\right)}^6$ là

A. $2^2{C}_6^2$

B. $2^4{C}_6^2$

C. $2^3{C}_6^3$

D. $-2^2{C}_6^4$

Lời giải

Ta có ${\left(x^2+\frac{2}{x^2}\right)}^6=\sum _{k=0}^6{C}_6^k{\left(x^2\right)}^{6-k}.{\left(\frac{2}{x^2}\right)}^k=\sum _{k=0}^6{C}_6^k.x^{12-2k}.\frac{2^k}{x^{2k}}=\sum _{k=0}^6{C}_6^k{.2}^k.x^{12-4k}$

Số hạng không chứa x khi $12-4k=0\iff k=3\Rightarrow$số hạng đó là $2^3{C}_6^3$

Chọn C.

Câu 44: Cho $\tan \alpha =-2$. Giá trị của biểu thức $P=\frac{\sin \alpha +3\cos \alpha }{2\cos \alpha -3\sin \alpha }$

A. $-\frac{1}{8}$

B. $\frac{1}{5}$

C. $-\frac{1}{5}$

D. $\frac{1}{8}$

Lời giải

Ta có $P=\frac{\sin \alpha +3\cos \alpha }{2\cos \alpha -3\sin \alpha }=\frac{\frac{\sin x}{\cos x}+3}{2-3\frac{\sin x}{\cos x}}=\frac{\tan x+3}{2-3\tan x}=\frac{1}{8}$

Chọn D.

Câu 45: Phương trình $\sin 8x-\cos 6x=\sqrt{3}(\sin 6x+\cos 8x)$ có các họ nghiệm là:

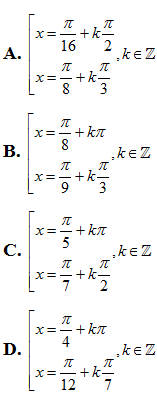
Lời giải

Ta có $\sin 8x-\cos 6x=\sqrt{3}\left(\sin 6x+\cos 8x\right)\iff \sin 8x-\sqrt{3}\cos 8x=\sqrt{3}\sin 6x+\cos 6x$

$\begin{array}{l}\iff \frac{1}{2}\sin 8x-\frac{\sqrt{3}}{2}\cos 8x=\frac{\sqrt{3}}{2}\sin 6x+\frac{1}{2}\cos 6x\\ \iff \sin 8x\cos \frac{\pi }{3}-\sin \frac{\pi }{3}\cos 8x=\sin 6x\cos \frac{\pi }{6}+\sin \frac{\pi }{6}\cos 6x\end{array}$

$$\begin{gathered} \iff \sin \left(8x-\frac{\pi }{3}\right)=\sin \left(6x+\frac{\pi }{6}\right)\iff \left[\begin{array}{l}8x-\frac{\pi }{3}=6x+\frac{\pi }{6}+k2\pi \\ 8x-\frac{\pi }{3}=\frac{5\pi }{6}-6x+k2\pi \end{array}\right. \\ \iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\frac{\pi }{12}+k\frac{\pi }{7}\end{array}\right. \end{gathered}$$

Chọn D.

Câu 46: Trong mặt phẳng tọa độ Oxy cho điểm M'(-3; 2) là ảnh của điểm M qua phép quay tâm O góc 90^o thì điểm M có tọa độ là:

A. $(2; -3)$

B. $(2; 3)$

C. $(-2; -3)$

D. $(3; -2)$

Lời giải

Điểm M(-3; 2) là ảnh của điểm M(2; 3) qua phép quay tâm O góc 90⁰

Chọn B.

Câu 47: Tính $S=C_{2008}^1+C_{2008}^2+C_{2008}^3+...+C_{2008}^{2017}$

A. $2^{2018}-1$

B. $2^{2018}+1$

C. $2^{2018}$

D. $2^{2018}-2$

Lời giaỉ

Ta có ${\left(x+1\right)}^{2018}=C_{2018}^0+C_{2018}^{1}x+\mathrm{...}+C_{2018}^{2018}{x}^{2018}$

Chọn $x=1\Rightarrow C_{2018}^0+C_{2018}^1+\mathrm{...}+C_{2018}^{2018}=2^{2018}$

$\iff C_{2018}^1+C_{2018}^2+C_{2018}^3+\mathrm{...}+C_{2018}^{2017}=2^{2018}-C_{2018}^0-C_{2018}^{2018}=2^{2018}-1-1$

$\iff C_{2018}^1+C_{2018}^2+C_{2018}^3+\mathrm{...}+C_{2018}^{2017}=2^{2018}-2$

Chọn D.

Câu 48: Trong mặt phẳng  cho đường thẳng d: x + 2y - 3 = 0. Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 2 và phép tịnh tiến theo vector $\overrightarrow{v}=(1; 2)$ biến d thành đường thẳng d’ có phương trình:

A. $x+2y-6=0$

B. $x+2y-11=0$

C. $x+2y+6=0$

D. $x+2y+11=0$

Lời giải

Gọi (x; y) là điểm thuộc đường thẳng d, M'(x'; y') là điểm thuộc đường thẳng d₁ là ảnh của d qua phép vị tự tâm O tỉ số k = 2, M''(x''; y'') là điểm thuộc đường thẳng d'' là ảnh của d₁ qua phép tịnh tiến theo vecto $\overrightarrow{v}=(1; 2)$

Ta có $V_{\left(O;k\right)}\left(M=M\text{'}\right)\Rightarrow \overrightarrow{OM\text{'}}=2\overrightarrow{OM}\iff \left\{\begin{array}{l}x\text{'}=2x\\ y\text{'}=2y\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{x\text{'}}{2}\\ y=\frac{y\text{'}}{2}\end{array}\right.\Rightarrow M\text{'}\left(\frac{x\text{'}}{2};\frac{y\text{'}}{2}\right)$

Ta có $T_{\overrightarrow{v}}\left(M\text{'}\right)=M"\iff \left\{\begin{array}{l}x"=x\text{'}+1\\ y"=y\text{'}+2\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=x"-1\\ y=y"-2\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{x"-1}{2}\\ y=\frac{y"-2}{2}\end{array}\right.\Rightarrow M\left(\frac{x"-1}{2};\frac{y"-2}{2}\right)$

Mà $M\in d:x+2y-3\Rightarrow \frac{x"-1}{2}+2\frac{y"-2}{2}-3\iff x"+2y"-11=0\Rightarrow d\text{'}:x+2y-11=0$

Chọn B.

Câu 49: Tập xác định của hàm số $y=\sqrt{x-1}+\frac{1}{x-3}$ là:

A. $(1; +\infty ) \backslash \left\{3\right\}$

B. $[1; +\infty )$

C. $[1; 3]$

D. $[1; +\infty ) \backslash 3$

Lời giải

Điều kiện: $\left\{\begin{array}{l}x-1\ge 0\\ x-3\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ge 1\\ x\ne 3\end{array}\right.\Rightarrow D=\text{\hspace{0.17em}\hspace{0.17em}[}1;+\text{}\infty )\backslash \left\{3\right\}$

Chọn D.

Câu 50: Trong các giá trị sau, giá trị nào là nghiệm của phương trình: $cotx=-\frac{\sqrt{3}}{3}$

A. $x=\frac{\mathrm{\pi }}{6}+k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

B. $x=\frac{\mathrm{\pi }}{3}+k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

C. $x=-\frac{\mathrm{\pi }}{3}+k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

D. $x=-\frac{\mathrm{\pi }}{6}+k\mathrm{\pi }, \mathrm{k}\in \mathrm{\mathbb{Z}}$

Lời giải

Ta có $\cot x=-\frac{\sqrt{3}}{3}\iff x=-\frac{\pi }{3}+k\pi$

Chọn C

Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:

TOP 30 Đề thi Giữa Học kì 2 Toán lớp 11 năm 2022 có đáp án

Đề cương Giữa học kì 2 Toán lớp 11 năm 2022 chi tiết nhất

Bài tập Toán lớp 11 Giữa học kì 2 có đáp án

Các dạng bài tập Toán lớp 11 giữa học kì 2

Hệ thống kiến thức Toán lớp 11 Giữa học kì 2