TOP 30 Đề thi Giữa Học kì 2 Toán lớp 11 năm 2024 có đáp án (sách mới) | Kết nối tri thức, Chân trời sáng tạo, Cánh diều
30 Đề thi Giữa Học kì 2 Toán lớp 11 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 11 học kì 2. Mời các bạn cùng đón xem
Đề thi Toán 11 Giữa Học kì 2 năm 2024 có đáp án (cả 3 sách)
Đề thi Giữa Học kì 2 Toán lớp 11 (Kết nối tri thức) 2024 có đáp án
Đề thi Giữa Học kì 2 Toán lớp 11 (Chân trời sáng tạo) 2024 có đáp án
Đề thi Giữa học kì 2 Toán lớp 11 (Cánh diều) 2024 có đáp án
Đề thi Giữa Học kì 2 Toán lớp 11 năm 2024 có đáp án
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng giữa học kì 2
Năm học ...
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi Giữa Học kì 2 Toán lớp 11 có đáp án Đề số 1
Câu 1. Cho dãy số thỏa mãn Giá trị của bằng:
A. -2
B. 2
C. 1
D. 0
Câu 2. bằng:
A.
B.
C. 1
D. 2
Câu 3. Cho hai dãy số thỏa mãn và Giá trị của bằng
A. 2
B. 8
C. -2
D. 6
Câu 4. bằng
A. 1
B.
C. 0
D.
Câu 5. bằng
A.
B.
C. 2
D. 0
Câu 6. Cho hai dãy số thỏa mãn và Giá trị của bằng
A. 6
B. 5
C. 1
D. -1
Câu 7. Cho dãy số thỏa mãn Giá trị của bằng
A. -3
B. 3
C. 10
D. -10
Câu 8. Cho hai hàm số thỏa mãn và Giá trị của bằng
A. 5
B. 6
C. 1
D. -1
Câu 9. Cho hàm số thỏa mãn và Giá trị của bằng
A. 2
B. 1
C.
D.
Câu 10. bằng:
A. 3
B. 1
C.
D.
Câu 11. bằng
A.
B. 1
C. 2
D. -3
Câu 12. Giá trị của bằng
A. 2
B. 1
C.
D. 0
Câu 13. Tính giới hạn
A.
B.
C.
D.
Câu 14 bằng
A. 2
B. 4
C. -1
D. -4
Câu 15. Tính giới hạn
A.
B.
C. 2
D. 0
Câu 16. Tính
A. L = -2
B. L = -1
C. L =
D. L = 2
Câu 17. Tính
A. -4
B. -2
C. 4
D. 2
Câu 18. Giới hạn bằng
A.
B. 3
C. -3
D.
Câu 19. Tính bằng
A.
B.
C.
D. 1
Câu 20. Hàm số gián đoạn tại điểm nào dưới đây?
A.
B.
C.
D.
Câu 21. Hàm số liên tục tại điểm nào dưới đây?
A.
B.
C.
D.
Câu 22. Hàm số liên tục trên khoảng nào dưới đây?
A.
B. (0 ; 3)
C. (4; 6)
D. (2; 5)
Câu 23. Cho hàm số Giá trị của tham số m để hàm số liên tục tại bằng
A. 2
B. -2
C. 1
D. -1
Câu 24. Hàm số nào dưới đây liên tục trên khoảng ?
A.
B.
C.
D.
Câu 25. Hàm số nào dưới đây liên tục trên ?
A.
B.
C.
D.
Câu 26. Cho hai đường thẳng a, l song song với nhau và mặt phẳng cắt l. Ảnh của a qua phép chiếu song song lên theo phương l là:
A. một đường thẳng.
B. một điểm.
C. một tia.
D. một đoạn thẳng.
Câu 27. Cho hình hộp ABCD.A'B'C'D'. Ta có bằng
A.
B.
C.
D.
Câu 28. Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt ; ; . Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Câu 29. Cho tứ diện ABCD . Đặt . Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Câu 30. Cho ba vectơ không đồng phẳng. Xét các vectơ . Chọn khẳng định đúng?
A. Hai vectơ cùng phương.
B. Hai vectơ cùng phương.
C. Hai vectơ cùng phương.
D. Ba vectơ đồng phẳng.
Câu 31. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
Câu 32. Cho hình lập phương (tham khảo hình vẽ).
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c32-1649494113.png)
Góc giữa đường thẳng AD và BB1 bằng:
A. 90o
B. 30o
C. 45o
D. 60o
Câu 33. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc bằng:
A. 60o
B. 30o
C. 45o
D. 90o
Câu 34.Cho hình lập phương . Gọi M, N , P lần lượt là trung điểm của các cạnh AB, AC, C'D'.
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c34-1649494310.png)
Cosin của góc giữa hai đường thẳng MN, CP bằng
A.
B.
C.
D.
Câu 35. Cho tứ diện ABCD có và , . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ và ?
A. 120o
B. 90o
C. 45o
D. 45o
PHẦN TỰ LUẬN
Bài 1 ( 1 điểm). Xác định a để hàm số liên tục trên .
Bài 2 (1 điểm). Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD biết . Tính góc giữa hai đường thẳng AB và CD.
Bài 3 (0,5 điểm). Tìm hai số a, b biết rằng và .
Bài 4 ( 0,5 điểm). Tính
I =
HƯỚNG DẪN ĐÁP ÁN VÀ THANG ĐIỂM
I. PHẤN TRẮC NGHIỆM
BẢNG ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
B |
A |
D |
C |
A |
A |
B |
A |
A |
A |
B |
D |
B |
D |
B |
D |
B |
A |
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
|
A |
B |
D |
C |
B |
D |
C |
B |
D |
A |
A |
B |
D |
A |
A |
C |
B |
|
* Mỗi câu trắc nghiệm đúng được 0,2 điểm.
II. PHẦN TỰ LUẬN
|
Câu hỏi |
Nội dung |
Điểm |
|
Bài 1 (1,0 điểm) |
Hàm số xác định trên Với hàm số liên tục Với hàm số liên tục Với x = 2 ta có
Hàm số liên tục trên hàm số liên tục tại x = 2
Vậy là những giá trị để hàm sôố liên tục trên . |
0,25
0,25
0,25
0,25 |
|
Bài 2 (1,0 điểm) |
Cách 1. Gọi I là trung điểm của AC. Ta có Đặt xét tam giác IMN có: Theo định lí côsin, ta có
suy ra Cách 2:
Vậy |
0,25
0,25
0,25 0,25
0,25
0,25
0,25
0,25 |
|
Bài 3 (0,5 điểm) |
Ta có
Do đó ta có hệ |
0,25
0,25
|
|
Bài 4 (0,5 điểm) |
Ta có:
Mà Vậy I = 1 |
0,25
0,25 |
HƯỚNG DẪN CHI TIẾT 35 CÂU TRẮC NGHIỆM
Câu 1.
Chọn B
Ta có:
Câu 2.
Chọn A
Ta có:
Câu 3.
Chọn D
Ta có:
Câu 4.
Chọn C
Ta có:
Câu 5.
Chọn A
Câu 6.
Chọn A
Ta có:
Câu 7.
Chọn B
Ta có:
Câu 8.
Chọn A
Ta có:
Câu 9.
Chọn A
Ta có:
Câu 10.
Chọn A
Câu 11.
Chọn B
Chia cả tử và mẫu cho X, ta có
Câu 12.
Chọn D
Ta có:
Câu 13.
Chọn B
Ta có
Câu 14.
Chọn D
Câu 15.
Chọn B
Ta có
Câu 16.
Chọn D
Ta có
Câu 17.
Chọn B
Câu 18.
Chọn A
=
Câu 19.
Chọn A
Ta có:
Câu 20.
Chọn B
Hàm số là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định của nó là . Do đó, hàm số gián đoạn tại điểm .
Câu 21.
Chọn D
Hàm số là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định của nó là và
Do đó, hàm số liên tục tại điểm
Câu 22.
Chọn C
Hàm số là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định của nó là và .
Vì nên hàm số liên tục trên khoảng .
Câu 23.
Chọn B
Ta có và
Điều kiện cần và đủ để hàm số đã cho liên tục tại điểm là .
Câu 24.
Chọn D
Hàm số xác định và liên tục trên mỗi khoảng và . Ta có nên hàm số liên tục trên khoảng .
Câu 25.
Chọn C
Hàm số là hàm số đa thức nên liên tục trên , hàm số liên tục trên Do đó, hàm số liên tục trên .
Câu 26.
Chọn B
Phép chiếu song song biến đường thẳng song song với phương chiếu thành một điểm.
Câu 27.
Chọn D
Theo quy tắc hình hộp ta có
Câu 28.
Chọn A
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c28-1649568497.png)
Vì G là trọng tâm của tam giác BCD nên ta có
Suy ra ![]()
Câu 29.
Chọn A
Ta có
Câu 30.
Chọn B
+ Nhận thấy: nên hai vectơ cùng phương.
Câu 31.
Chọn D
Trong không gian một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Câu 32.
Chọn A
Câu 33.
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/3-1649568793.png)
Chọn A
Từ giả thiết ta có (do IJ là đường trung bình của và Mặt khác, ta lại có đều nên
Suy ra
Câu 34.
Chọn C
Đặt AD = 2a, gọi Q là trung điểm B'C' thì do đó
Ta có
Do đó
Vậy
Câu 35.
Chọn B
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c35-1649569354.png)
Xét tam giác ICD có J là trung điểm CD
Tam giác ABC có đều
Tương tự ta có đều nên
Ta có
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng giữa học kì 2
Năm học ...
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi Giữa Học kì 2 Toán lớp 11 có đáp án Đề số 2
Câu 1. Cho dãy số (un), biết . Số hạng đầu tiên của dãy số là:
A.
B.
C.
D.
Câu 2. Cho dãy số (un), biết với . Ba số hạng đầu tiên của dãy số đó lần lượt là:
A. 2; 3; 5
B. 2; 5; 11
C. -1; 2; 3
D. -1; 3; 7
Câu 3. Cho dãy số (un), biết . Tìm khẳng định sai
A. u1 = 0
B. (un) bị chặn trên
C. (un) là dãy số giảm
D.
Câu 4. Cho dãy số (un), biết . Tích của 2021 số hạng đầu tiên bằng
A.
B.
C.
D.
Câu 5. Cho dãy số (un), biết , . Số hạng thứ 10 của dãy số là:
A.
B. 336
C.
D.
Câu 6. Một cấp số cộng (un) có u1 = 2, u21 = 62. Công sai của cấp số cộng đó là
A. 2
B. 1
C. 4
D. 3
Câu 7. Tìm m để 3 số: 4; 5m + 1 ; 32 – 7m theo thứ tự lập thành cấp số cộng.
A. m = – 2
B. m = 2
C. m = 11
D. m = 1
Câu 8. Một cấp số cộng (un) có 8 số hạng, biết u1 = – 2, u8 = 32. Tổng các số hạng của cấp số cộng đó là
A. 136
B. 30
C. 120
D. 240
Câu 9. Cho cấp số cộng (un) có u1 = 1, công sai d = 3. Tìm số hạng tổng quát của cấp số cộng.
A.
B.
C.
D.
Câu 10. Cho cấp số cộng (un) thỏa mãn
Tính
A. 2 043 231
B. 2 043 230
C. 2043 905
D. 2 042 220
Câu 11. Cho cấp số cộng (un), biết u2 = 4 và u4 = 6. Giá trị của u9 bằng
A. 11
B. 10
C. 9
D. 8
Câu 12. Cho cấp số nhân (un) có số hạng thứ ba u3 = 7 và số hạng thứ năm u5 = 28. Biết công bội là một số dương khi đó công bội của cấp số nhân (un) là
A. 4
B.
C. 2
D. 21
Câu 13. Cho cấp số nhân (un) có số hạng thứ nhất u1 = 16, công bội . Số hạng thứ mười u10 là
A. 32
B.
C. 120
D.
Câu 14. Cho cấp số nhân (un) có số hạng đầu u1 = – 2, công bội q = 3. Số –39366 là số hạng thứ mấy của cấp số nhân đã cho?
A. 10
B. 9
C. 8
D. 11
Câu 15. Cho cấp số nhân (un) biết số hạng đầu u1 = 2, công bội q = –2. Tổng 10 số hạng đầu của cấp số nhân là
A. 2046
B. -2046
C. 682
D. -682
Câu 16. Cho cấp số nhân (un) có S5 = 30, S10 = 50. Tìm công bội q của cấp số nhân.
A. q = 2
B.
C.
D.
Câu 17. Tập nghiệm của phương trình là.
A.
B.
C.
D.
Câu 18. Giá trị của bằng
A.
B.
C.
D. 1
Câu 19. Dãy số nào sau đây có giới hạn bằng 0?
A.
B.
C.
D.
Câu 20. Tính
A. 1
B. 3
C.
D. 2
Câu 21. Tính
A. 1
B. 3
C.
D. 2
Câu 22. Giá trị của bằng:
A.
B.
C. 2
D. 0
Câu 23. Giá trị của là
A.
B.
C.
D.
Câu 24. Biết , với . Tính
A.
B.
C.
D.
Câu 25. Biết với và tối giản. Tính
A. 8
B. -8
C. -2
D. 10
Câu 26. Cho hình hộp ABCD.A'B'C'D'. Đường thẳng BD không song song với mặt phẳng nào dưới đây
A.
B.
C.
D.
Câu 27. Cho tứ diện ABCD. Gọi M, N, P lần lượt nằm trên các cạnh AB, AC, AD sao cho AM = 2MB, AN = 2NC, AP = PD. Mệnh đề nào sau đây là mệnh đề đúng?
A. ND // (ABC)
B. MP // (BCD)
C. NP // (BCD)
D. MN // (BCD)
Câu 28. Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng d nằm trong mặt phẳng (P). Khẳng định nào là khẳng định đúng?
A. d có thể cắt (Q) hoặc nằm trong (Q)
B. d nằm trong (Q)
C. d cắt (Q)
D. d song song với (Q)
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi A', B', C' lần lượt là trung điểm của các cạnh SA, SB, SC. Khẳng định nào sau đây là khẳng định đúng?
A.
B.
C.
D.
Câu 30. Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sai trong các mệnh đề sau?
A.
B.
C.
D.
Câu 31. Cho tứ diện ABCD có G là trọng tâm tứ diện. Khi hệ thức véc tơ đúng với mọi điểm M thì giá trị của k là
A.
B. k = 1
C.
D.
Câu 32. Cho hình chóp S.ABCD, ABCD là hình bình hành, tam giác SAB là tam giác đều cạnh a. Tính tích vô hướng ?
A.
B.
C.
D.
Câu 33. Trong không gian, khẳng định nào sau đây sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau
B. Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
C. Hai đường thẳng vuông góc với nhau thì góc giữa chúng bằng 90°.
D. Nếu và thì .
Câu 34. Cho hình chóp S.ABCD, có đáy ABCD là hình thoi góc bằng 120°. Gọi M, N lần lượt là trung điểm của SA và SC. Số đo góc giữa hai đường thẳng MN và BC bằng
A. 30°.
B. 60°.
C. 45°.
D. 90°.
Câu 35. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2a, . Gọi I là trung điểm của đoạn thẳng AC. Tính côsin góc giữa hai đường thẳng SA và BC biết SI vuông góc với cả hai đường thẳng AC và BI.
A.
B.
C.
D.
II. PHẦN TỰ LUẬN
Câu 1. Cho dãy số (un) với
Khi đó tổng trong đó a, b, c là các số nguyên dương.
Tính a + 2b2 – 2c.
Câu 2. Cho dãy số (un) thỏa mãn . Tìm giới hạn .
Câu 3. Cho hình lập phương ABCD.A'B'C'D'. M, N lần lượt thuộc các đoạn AD, A'C sao cho . Chứng minh:
a) (AB'D') // (BC'D).
b)
c) MN // (AB'D').
ĐÁP ÁN
I. Bảng đáp án.
|
1.D |
2.A |
3.C |
4.C |
5.A |
6.D |
7.B |
8.C |
9.C |
10.C |
|
11.A |
12.C |
13.D |
14.A |
15.D |
16.D |
17.B |
18.C |
19.B |
20.C |
|
21.B |
22.A |
23.A |
24.A |
25.B |
26.D |
27.D |
28.D |
29.B |
30.A |
|
31.D |
32.D |
33.A |
34.A |
35.B |
|
|
|
|
|
II. Hướng dẫn giải chi tiết.
I. Phần trắc nghiệm
Câu 1.
Lời giải
Ta có:
Câu 2.
Lời giải
Ta có
u1 = 2
Vậy ba số hạng đầu tiên của dãy số lần lượt là: 2; 3; 5
Chọn D.
Câu 3.
Lời giải
* Ta có . Phương án A đúng.
* Ta có
Suy ra: nên bị chặn trên. Phương án B đúng.
* Ta có:
Suy ra (un) là dãy số tăng. Phương án C sai.
* Ta có: . Phương án D đúng.
Vậy khẳng định sai là: “ (un) là dãy số giảm”.
Chọn C.
Câu 4.
Lời giải
Ta có:
Suy ra:
Chọn C.
Câu 5.
Lời giải
Ta có:
Chọn A.
Câu 6.
Lời giải
Áp dụng công thức số hạng tổng quát của cấp số cộng
ta có:
Vậy công sai của cấp số cộng đó là 3.
Chọn D.
Câu 7.
Lời giải
Áp dụng tính chất của cấp số cộng với ta có:
Ba số: 4; 5m+1; 32-7m theo thứ tự lập thành cấp số cộng
Vậy m = 2 thỏa mãn đề bài.
Chọn B.
Câu 8.
Lời giải
Ta có tổng của 8 số hạng của cấp số cộng
Chọn C.
Câu 9.
Lời giải
Áp dụng công thức số hạng tổng quát ta có:
Chọn C.
Câu 10.
Lời giải
Cấp số cộng (un) có công sai là d .
Ta có hệ phương trình:
là một cấp số cộng (Vn) có: , công sai d' = 9, n = 674
Chọn C.
Câu 11.
Lời giải
Cấp số cộng (un) có công sai là d.
Ta có hệ phương trình:
Vậy
Chọn A.
Câu 12.
Lời giải
Cấp số nhân (un) có công bội là q.
Ta có hệ phương trình:
Mà q > 0 nên q = 2.
Chọn C.
Câu 13.
Lời giải
Ta có số hạng thứ mười
Chọn D.
Câu 14.
Lời giải
Gọi un là số hạng thứ n của dãy.
Ta có: số hạng tổng quát của cấp số nhân:
Vậy –39366 là số hạng thứ 10.
Chọn A.
Câu 15.
Lời giải
Tổng 10 số hạng đầu của cấp số nhân:
Chọn D.
Câu 16.
Lời giải
+) Trường hợp q = 1.
Ta có
Khi đó từ giả thiết ta có:
+) Trường hợp
Theo giả thiết ta có
Chia vế cho vế của (2) cho (1) ta được:
Chọn D.
Câu 17.
Lời giải
Nhận xét: x = 0 không phải là nghiệm của phương trình đã cho.
Ta có vế trái của phương trình đã cho là tổng của 10 số hạng đầu của một cấp số nhân có số hạng đầu và công bội
Phương trình đã cho trở thành:
Vậy tập nghiệm của phương trình đã cho là
Chọn B.
Câu 18.
Lời giải
Chọn C.
Câu 19.
Lời giải
Ta có nếu
Mà
Do đó .
Chọn B.
Câu 20.
Lời giải
Ta có khi
Áp dụng kết quả , ta có
Vậy
Chọn C.
Câu 21.
Lời giải
Ta có
Chọn B.
Câu 22.
Lời giải
Chọn A.
Câu 23.
Lời giải
Chọn A.
Câu 24.
Lời giải
Vậy
Chọn A.
Câu 25.
Lời giải
Cách 1:
Ta có
Khi đó
Ta có a = 1, b = 3. Vậy
Cách 2: (Cấp số nhân lùi vô hạn).
Đặt
Có , nên (un) là cấp số nhân lùi.
Ta có a = 1, b = 3. Vậy
Chọn B.
Câu 26.
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c26-1649728305.png)
Đường thẳng BD và mặt phẳng (BA'C') có chung điểm B nên đường thẳng BD không song song với mặt phẳng (BA'C').
Chọn D.
Câu 27.
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c27-1649728344.png)
Ta nhận thấy N nằm trên mặt phẳng (ABC) nên đường thẳng ND không song song với mặt phẳng (ABC). Vậy đáp án A sai.
Từ giả thiết suy ra nên MP cắt BD, do đó đường thẳng MP không song song với mặt phẳng (BCD).
Tương tự ta lại có NP cắt CD nên đường thẳng NP không song song với mặt phẳng (BCD).
Mặt khác MN // BC và MN không nằm trên mặt phẳng (BCD) nên MN // (BCD).
Chọn D.
Câu 28.
Lời giải
d và (Q) không có điểm chung hay d song song với (Q).
Chọn D.
Câu 29.
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c29-1649728492.png)
Ta có:
Từ (1), (2)
+ Đáp án A sai vì
+ Đáp án C sai vì
+ Đáp án D sai vì
Chọn B.
Câu 30.
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c30-1649728640.png)
+) Theo quy tắc hình bình hành ta có nên đáp án A sai.
+) Theo quy tắc hình hộp ta có nên đáp án B đúng.
+) Theo quy tắc hình bình hành ta có nên đáp án C đúng.
+) Theo quy tắc hình bình hành ta có nên đáp án D đúng.
Chọn A.
Câu 31.
Lời giải
G là trọng tâm tứ diện ABCD
, với mọi điểm M.
, với mọi điểm M.
Vậy
Chọn D.
Câu 32:
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c322-1649728925.png)
Tam giác SAB là tam giác đều cạnh a suy ra SA = AB = a và
Do nên
Vậy
Chọn D.
Câu 33:
Lời giải
Xét hình lập phương ABCD.A'B'C'D', ta có nhưng AB và AD cắt nhau. Do đó phương án A sai.
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c333-1649729128.png)
Chọn A.
Câu 34.
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c34-1649729194.png)
+ Vì M, N lần lượt là trung điểm của SA và SC suy ra MN song song AC.
+
+) Tứ giác ABCD là hình thoi có
Vậy
Chọn A.
Câu 35.
Lời giải
+ Vì tam giác ABC là tam giác đều suy ra IB vuông góc với AC.
+ Ta có:
+
Chọn B.
II. PHẦN TỰ LUẬN
Câu 1.
Lời giải
Ta có
Mà nên
Nên
Câu 2.
Lời giải
+) Ta có:
+) Đặt . Ta có và
Suy ra dãy (vn) là cấp số nhân với công bội là q = 2021,
Khi đó
Do đó
+) Ta có:
Vậy
Câu 3.
Lời giải
![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/c3tl-1649729804.png)
a) Chứng minh
Từ giả thiết ta có
b) Chứng minh
Ta có:
c) Chứng minh .
Dễ thấy M, N không thuộc (AB'D').
đồng phẳng
Đặt
Vậy MN // (AB'D').
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng giữa học kì 2
Năm học ...
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi Giữa Học kì 2 Toán lớp 11 có đáp án Đề số 3
I. PHẦN TRẮC NGHIỆM
Câu 1: Cho dãy số thỏa mãn Giá trị của bằng:
A. 2
B. -2
C. 1
D. 0
Câu 2: bằng
A.
B.
C. 1
D. 2
Câu 3: Cho hai dãy số thỏa mãn và Giá trị của bằng
A. 6
B. 8
C. -2
D. 2
Câu 4: bằng:
A. 0
B.
C. 1
D.
Câu 5: bằng:
A.
B.
C. 2
D. 0
Câu 6: Cho hai dãy số thỏa mãn và Giá trị của bằng
A. 6
B. 5
C. -6
D. -1
Câu 7: Cho dãy số thỏa mãn Giá trị của bằng
A. 3
B. -7
C. 10
D. - 10
Câu 8: Cho hai hàm số thỏa mãn và Giá trị của bằng:
A. 5
B. 6
C. 1
D. -1
Câu 9: Cho hàm số thỏa mãn và Giá trị của bằng:
A. 2
B. 1
C. -4
D. 0
Câu 10: bằng:
A. 3
B. 1
C.
D.
Câu 11: bằng:
A. 2
B. 4
C. 0
D. 1
Câu 12: bằng:
A.
B.
C. 0
D. 1
Câu 13: Cho hai hàm số thỏa mãn và Giá trị của bằng
A.
B.
C. 2
D. -2
Câu 14: Hàm số gián đoạn tại điểm nào dưới đây ?
A. x = 1
B. x = 0
C. x = 2
D. x = -1
Câu 15: Hàm số liên tục tại điểm nào dưới đây ?
A. x = -1
B. x = 0
C. x = 1
D. x = 2
Câu 16: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng
Câu 17: Cho ba điểm A, B, C tùy ý. Mệnh đề nào dưới đây đúng ?
A.
B.
C.
D.
Câu 18: Cho hình hộp
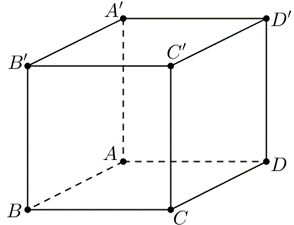
Ta có bằng
A.
B.
C.
D.
Câu 19: Với hai vectơ khác vectơ - không tùy ý, tích vô hướng bằng
A.
B.
C.
D.
Câu 20: Cho hai đường thẳng a và b vuông góc với nhau. Gọi hai vectơ lần lượt là vectơ chỉ phương của a và b. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Câu 21: bằng:
A. -2
B.
C.
D.
Câu 22: Cho cấp số nhân lùi vô hạn có và công bội Tổng của cấp số nhân lùi vô hạn đã cho bằng
A. 2
B. 4
C. 3
D. 5
Câu 23: bằng
A. 3
B. -3
C. 0
D.
Câu 24: bằng
A.
B.
C. 2
D.
Câu 25: bằng
A.
B. -1
C. 2
D.
Câu 26: bằng
A. -2
B. 4
C. 2
D. -1
Câu 27: Hàm số liên tục trên khoảng nào dưới đây?
A.
B.
C.
D.
Câu 28: Cho hàm số Giá trị của tham số m để hàm số liên tục tại x = 2 bằng:
A. 4
B. 2
C. 0
D. 5
Câu 29: Hàm số nào dưới đây liên tục trên khoảng ?
A.
B.
C.
D.
Câu 30: Hàm số nào dưới đây liên tục trên
A.
B.
C.
D.
Câu 31: Cho tứ diện đều ABCD. Góc giữa hai đường thẳng BC, AD bằng
A.
B.
C.
D.
Câu 32: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC. Góc giữa hai đường thẳng AB, AC bằng:
A.
B.
C.
D.
Câu 33: Trong không gian cho hai vectơ có và Độ dài của vectơ bằng:
A.
B. 7
C. 11
D.
Câu 34: Cho tứ diện ABCD. Gọi điểm G là trọng tâm tam giác ABD. Mệnh đề nào dưới đây đúng ?
A.
B.
C.
D.
Câu 35: Cho hình hộp . Trong các khẳng định sau, khẳng định nào sai?
A.
B.
C.
D.
II. PHẦN TỰ LUẬN
Câu 1
a) Tính
b)
Câu 2: Cho tứ diện ABCD. Trên cạnh AD lấy điểm M sao cho và trên cạnh BC lấy điểm N sao cho Chứng minh rằng ba vectơ và đồng phẳng.
Câu 3:
a) Tìm các số thực a, b thỏa mãn
b) Với mọi giá trị thực của tham số m, chứng minh phương trình luôn có nghiệm thực.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng giữa học kì 2
Năm học ...
Môn: Toán 11
Thời gian làm bài: 45 phút
Đề thi Giữa Học kì 2 Toán lớp 11 có đáp án Đề số 4
I. PHẦN CÂU HỎI TRẮC NGHIỆM (5,0 điểm).
Câu 1: Dãy số nào sau đây không phải là cấp số nhân?
A.
B.
C.
D.
Câu 2: Xác định x để 3 số lập thành một cấp số nhân:
A.
B. Không có giá trị nào của x
C.
D.
Câu 3: Tìm
A. 4
B. 8
C. 1
D. 2
Câu 4: Giá trị của là:
A.
B.
C. 1
D.
Câu 5: Giá trị của là:
A.
B.
C. 1
D. 0
Câu 6: Giới hạn bằng
A.
B.
C.
D.
Câu 7: Giới hạn bằng
A.
B. 0
C.
D.
Câu 8: bằng.
A. 2
B. -2
C.
D. 1
Câu 9: Giới hạn bằng
A. 1
B.
C.
D. 0
Câu 10: Giới hạn bằng
A.
B.
C.
D.
Câu 11: Cho Giới hạn bằng
A.
B.
C. 16
D. 3
Câu 12: Cho hàm số . Khi đó hàm số liên tục trên các khoảng nào sau đây?
A.
B.
C.
D.
Câu 13: Giá trị của tham số a để hàm số liên tục tại điểm x = 1 là
A.
B.
C.
D.
Câu 14: Cho hàm số Khẳng định nào sau đây đúng nhất ?
A. Hàm số liên tục tại mọi điểm.
B. Hàm số không liên tục tại x = 1
C. Hàm số liên tục tại x = 1
D. Tất cả đều sai.
Câu 15: Cho . Số gia của hàm số tại là
A.
B.
C.
D.
Câu 16: Cho . Đạo hàm của hàm số tại là
A.
B.
C.
D.
Câu 17: Cho . Phương trình tiếp tuyến với đồ thị của hàm số tại là
A.
B.
C.
D.
Câu 18: Cho hình chóp S.ABCD. Gọi A', B', C', D' lần lượt là trung điểm của các cạnh SA, SA, SC và SD. Trong các đường thẳng sau đây, đường thẳng nào không song song với A'B'?
A. SC
B. CD
C. C'D'
D. AB
Câu 19: Trong không gian, cho 3 đường thẳng a, b, c biết , a và c chéo nhau. Khi đó hai đường thẳng b và c:
A. Cắt nhau hoặc chéo nhau
B. Chéo nhau hoặc song song.
C. Song song hoặc trùng nhau.
D. Trùng nhau hoặc chéo nhau.
Câu 20: Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
B. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
D. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
Câu 21: Trong các mệnh đều sau, mệnh đề nào đúng?
A. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
B. Các cạnh bên của hình chóp cụt là các hình thang.
C. Các cạnh bên của hình chóp cụt đôi một song song.
D. Cả 3 mệnh đề trên đều sai.
Câu 22: Cho đường thẳng và đường thẳn . Mệnh đề nào sau đây đúng ?
A.
B.
C. và
D. a và b chéo nhau
Câu 23: Cho hình lăng trụ . Gọi M, N lần lượt là trung điểm của BB' và CC', . Khẳng định nào sau đây đúng ?
A.
B.
C.
D.
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
A.
B. cắt
C.
D.
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O có AC = a, BD = b. Tam giác SBD là tam giác đều. Một mặt phẳng di động song song với mặt phẳng (SBD) và đi qua điểm I trên đoạn AC và AI = x. Thiết diện của hình chóp cắt bởi là hình gì?
A. Hình bình hành
B. Tam giác
C. Tứ giác
D. Hình thang
II. PHẦN CÂU HỎI TỰ LUẬN (5,0 điểm).
Câu 1 (1,0 điểm). Cho cấp số nhân có công bội . Tìm .
Câu 2 (1,0 điểm). Tìm
Câu 3 (1,0 điểm). Cho hàm số . Tìm giá trị của tham số m để hàm số liên tục tại .
Câu 4 (1,0 điểm). Cho tứ diện ABCD có cạnh a. Gọi A’,B’,C’,D’lần lượt là trọng tâm các tam giác BCD, CDA, DAB và ABC.
a) Chứng minh rằng tứ diện A’B’C’D’ cũng là tứ diện đều.
b) Tính thể tích tứ diện A’B’C’D’ theo a.
....................
...................
....................
TẢI VỀ để xem trọn bộ đề thi Toán 11!
Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:
TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án
TOP 30 Đề thi Giữa học kì 2 Hóa học lớp 11 năm 2022 - 2023 có đáp án
TOP 30 Đề thi Giữa học kì 2 Ngữ văn lớp 11 năm 2022 - 2023 có đáp án
TOP 30 Đề thi Giữa học kì 2 Tiếng Anh lớp 11 có đáp án hay nhất
TOP 30 Đề thi Giữa học kì 2 Lịch sử lớp 11 năm 2022 - 2023 có đáp án
TOP 30 Đề thi Giữa học kì 2 Vật lí lớp 11 năm 2022 - 2023 có đáp án
TOP 30 Đề thi Giữa học kì 2 Sinh học lớp 11 năm 2022 - 2023 có đáp án
TOP 30 Đề thi Giữa học kì 2 Địa lí lớp 12 năm 2022 - 2023 có đáp án

![[Năm 2022] Đề thi Học kì 2 Toán lớp 11 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/ccccc-1649563965.png)