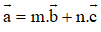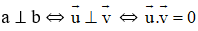Bài tập Toán lớp 11 Học kì 2 có đáp án
A. Bài tập Toán lớp 11 Học kì 2
- Bài tập Toán 11 Đại số và Giải tích
- Chương 1: Hàm số lượng giác và phương trình lượng giác
- Bài tập Hàm số lượng giác
- Bài tập Phương trình lượng giác cơ bản
- Bài tập Một số phương trình lượng giác thường gặp
- Bài tập Một số phương trình lượng giác cơ bản
- Chương 2: Tổ hợp - Xác suất mới nhất
- Bài tập Quy tắc đếm
- Bài tập Hoán vị - Chỉnh hợp - Tổ hợp
- Bài tập Nhị thức Niu - Tơn
- Bài tập Phép thử và biến cố
- Bài tập Xác suất của biến cố
- Chương 3: Dãy số - Cấp số cộng và cấp số nhân
- Bài tập Phương pháp quy nạp toán học - Dãy số
- Bài tập Cấp số cộng
- Bài tập Cấp số nhân
- Chương 4: Giới hạn
- Bài tập Giới hạn của dãy số
- Bài tập Giới hạn của hàm số
- Bài tập Hàm số liên tục
- Chương 5: Đạo hàm mới nhất
- Bài tập Định nghĩa và ý nghĩa của đạo hàm
- Bài tập Các quy tắc tính đạo hàm
- Bài tập Đạo hàm của các hàm số lượng giác
- Bài tập Vi phân
- Bài tập Đạo hàm cấp hai
- Bài tập Toán 11 Hình học
- Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
- Bài tập Phép biến hình. Phép tịnh tiến
- Bài tập Phép đối xứng trục
- Bài tập Phép đối xứng tâm
- Bài tập Phép quay
- Bài tập Khái niệm về phép dời hình và hai hình bằng nhau
- Bài tập Phép vị tự
- Bài tập Phép đồng dạng
- Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
- Bài tập Đại cương về đường thẳng và mặt phẳng
- Bài tập Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài tập Đường thẳng song song với mặt phẳng
- Bài tập Hai mặt phẳng song song
- Bài tập Phép chiếu song song. Hình biểu diễn của một hình không gian
- Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
- Bài tập Vectơ trong không gian
- Bài tập Hai đường thẳng vuông góc với nhau
- Bài tập Đường thẳng vuông góc với mặt phẳng
- Bài tập Mặt phẳng vuông góc
-
Bài tập Định nghĩa và ý nghĩa của đạo hàm - Toán 11
I. Bài tập trắc nghiệm
Bài 1: Xét ba mệnh đề sau: (1) Nếu hàm số f(x) có đạo hàm tại điểm x = x0 thì f(x) liên tục tại điểm đó. (2) Nếu hàm số f(x) liên tục tại điểm x = x0 thì f(x) có đạo hàm tại điểm đó. (3) Nếu f(x) gián đoạn tại x = x0 thì chắc chắn f(x) không có đạo hàm tại điểm đó. Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Lời giải:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f(x) liên tục tại điểm x = x0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R.
Nhưng ta có
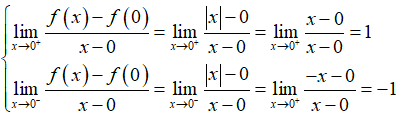
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.
Chọn đáp án A
Bài 2: Cho hàm số f(x) = x2 - x, đạo hàm của hàm số ứng với số gia của đối số x tại x0 là
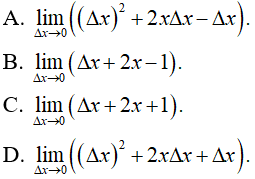
Lời giải:
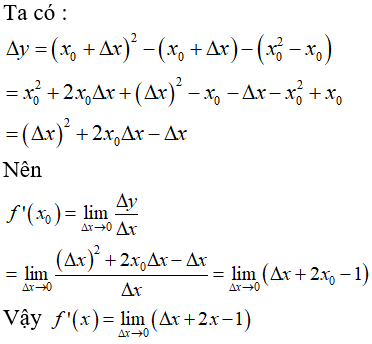
Chọn đáp án B
Bài 3: Xét hai câu sau: (1) Hàm số 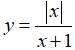 liên tục tại x= 0. (2) Hàm số
liên tục tại x= 0. (2) Hàm số 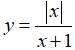 có đạo hàm tại x=0 . Trong hai câu trên:
có đạo hàm tại x=0 . Trong hai câu trên:
A. Chỉ có (2) đúng.
B. Chỉ có (1) đúng.
C. Cả hai đều đúng.
D. Cả hai đều sai.
Lời giải:
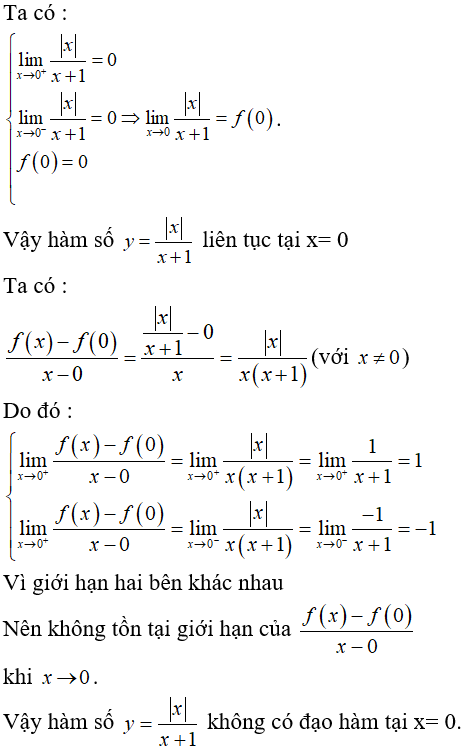
Chọn đáp án B
Bài 4: Cho hàm số f(x) = x2 + |x|. Xét hai câu sau: (1). Hàm số trên có đạo hàm tại x= 0 (2). Hàm số trên liên tục tại x= 0 Trong hai câu trên:
A. Chỉ (1) đúng.
B. Chỉ (2) đúng.
C. Cả hai đều đúng.
D. Cả hai đều sai.
Lời giải:
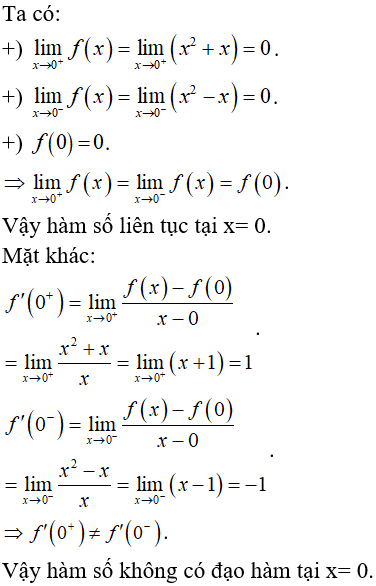
Chọn đáp án B
Bài 5: Tính đạo hàm của hàm số y = 2x2 + x + 1 tại điểm x = 2
A. 9
B. 4
C. 7
D. 6
Lời giải:
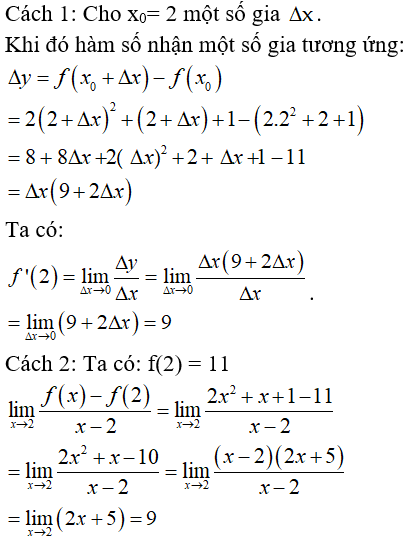
Kết luận theo định nghĩa, hàm số có đạo hàm tại x = 2 và f'(2) = 9.
Chọn đáp án A
Bài 6: Tính số gia của hàm số 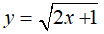 tại x0 = 1
tại x0 = 1
A.
B.
C.
D. Đáp án khác
Lời giải:
Cho x0 = 1 một số gia ∆x. Khi đó hàm số nhận một số gia tương ứng:
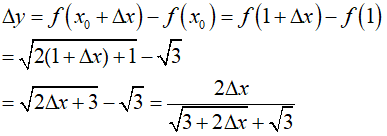
Chọn đáp án B
Bài 7: Tính đạo hàm của hàm số 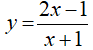 tại x = 3
tại x = 3
A. 16
B.316
C. 29
D. 45
Lời giải:
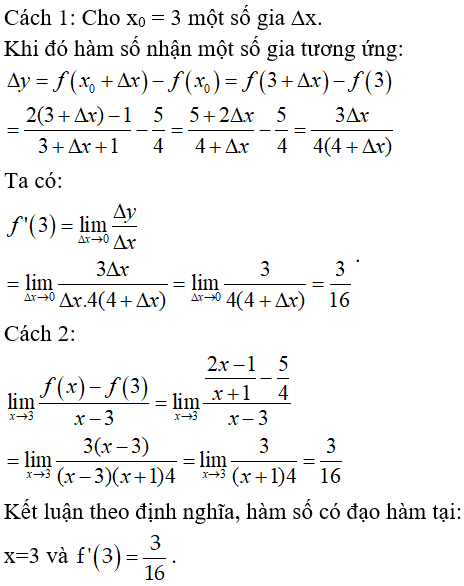
Chọn đáp án B
Bài 8: Tính đạo hàm của hàm số 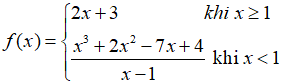 tại x0 = 1.
tại x0 = 1.
A. 0
B. 4
C. 5
D. Đáp án khác
Lời giải:
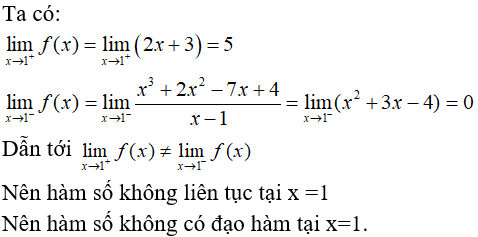
Chọn đáp án D
Bài 9: Cho hàm số 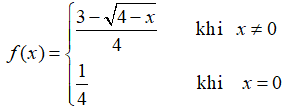 . Khi đó f'(0) là kết quả nào sau đây?
. Khi đó f'(0) là kết quả nào sau đây?
A. 14
B. 116
C. 132
D. Không tồn tại.
Lời giải:
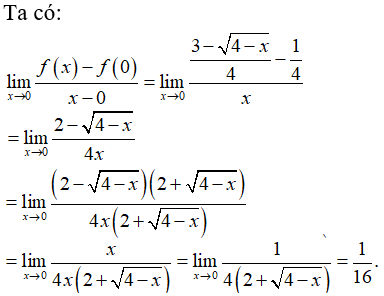
Chọn đáp án B
Bài 10: Cho hàm số 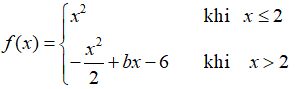 . Để hàm số này có đạo hàm tại x = 2 thì giá trị của b là
. Để hàm số này có đạo hàm tại x = 2 thì giá trị của b là
A. b = 3
B. b = -6
C. b = 1
D. b = 6
Lời giải:
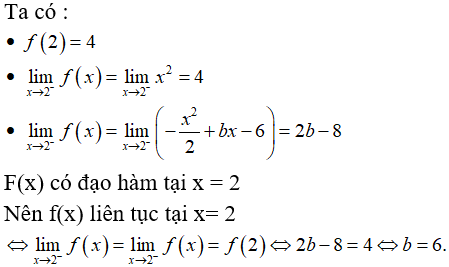
Chọn đáp án D
II. Bài tập tự luận có giải
Bài 1: Cho hàm số y = f(x) có đạo hàm tại x0 là f'(x0) . Khẳng định nào sau đây sai?
Lời giải:
Bài 2: Số gia của hàm số f(x) = x3 ứng với x0 = 2 và Δx = 1 bằng bao nhiêu?
Lời giải:
Gọi ∆x là số gia của đối số và ∆y là số gia tương ứng của hàm số.
Ta có :
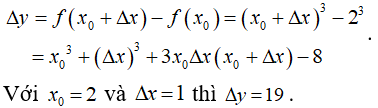
Bài 3: Tỉ số 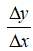 của hàm số f(x) = 2x.( x - 1) theo x và Δx là?
của hàm số f(x) = 2x.( x - 1) theo x và Δx là?
Lời giải:
Bài 4: Số gia của hàm số f(x) = x22 ứng với số gia Δx của đối số x tại x0 = -1 là
Lời giải:
Với số gia ∆x của đối số x tại x0 = -1 ,ta có:
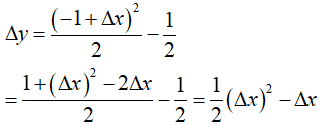
Bài 5: Tính đạo hàm của hàm số 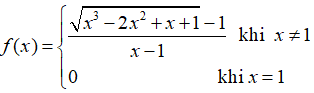 tại điểm x0 = 1.
tại điểm x0 = 1.
Lời giải:
Bài 6: Cho hàm số 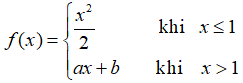 . Với giá trị nào sau đây của a, b thì hàm số có đạo hàm tại x = 1?
. Với giá trị nào sau đây của a, b thì hàm số có đạo hàm tại x = 1?
Lời giải:
Bài 7: Tính đạo hàm của hàm số 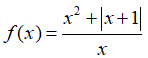 tại x = 1.
tại x = 1.
Lời giải:
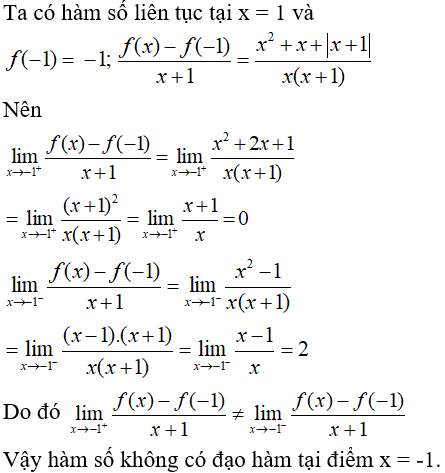
Nhận xét: Hàm số y = f(x) có đạo hàm tại x = x0 thì phải liên tục tại điểm đó.
Bài 8: Tìm số gia của hàm số f(x) = x3, biết rằng:
Lời giải:
Số gia của hàm số được tính theo công thức:
Δy = f(x) – f(x0) = f(x0 + Δx) – f(x0)
a. Δy = f(1 + 1) – f(1) = f(2) – f(1) = 23 – 13 = 7
b. Δy = f(1 – 0,1) – f(1) = f(0,9) – f(1) = (0,9)3 – 13 = -0,271.
Bài 9

Lời giải:

Bài 10 Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:
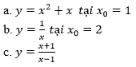
Lời giải:
y = x2 + x tại x0 = 1
*Giả sử Δx là số gia của đối số tại x0 = 1. Ta có:
∆Δy = f(x0+Δx)-f(x0) = f(1-Δx) = f(1)
= (1+Δx)2 +(1+Δx)-(12 +1)
= Δx(3+Δx)
* ΔxΔy = 3+x
* limΔxΔy = lim(3-Δx) = 3(vớiΔx →0)
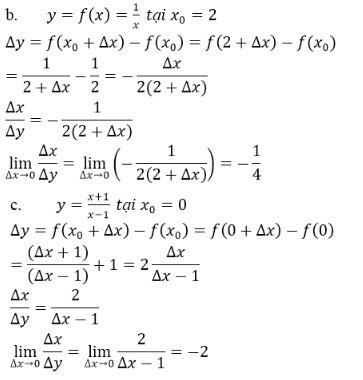
III. Bài tập vận dụng
Bài 1 Chứng minh rằng hàm số:
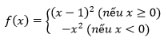
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.
Bài 2 Viết phương trình tiếp tuyến đường cong y = x3
a. Tại điểm (-1; -1);
b. Tại điểm có hoành độ bằng 2;
c. Biết hệ số góc của tiếp tuyến bằng 3.
Bài 3 Viết phương trình tiếp tuyến của hypebol y = 1/x

Bài 4 Một vật rơi tự do theo phương trình s=12 gt2, trong đó g≈9,8m/s2 là gia tốc trọng trường.
a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t+Δt, trong các trường hợp Δt = 0,1s; Δt = 0,05s; Δt = 0,001s.
b. Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.
Bài 5 Tìm số gia của hàm số f(x)=x3, biết rằng :
a) x0=1;∆
b)
Bài 6 Tính và của các hàm số sau theo và :
| a) ; |
b) ; |
| c) ; |
d) |
Bài 7 Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra:
a) tại ;
b) tại ;
c) tại .
Bài 8 Chứng minh rằng hàm số
không có đạo hàm tại điểm nhưng có đạo hàm tại điểm .
Bài 9 Viết phương trình tiếp tuyến của đường cong :
a) Tại điểm có tọa độ ;
b) Tại điểm có hoành độ bằng ;
c) Biết hệ số góc của tiếp tuyến bằng
Bài 10 Viết phương trình tiếp tuyến của đường hypebol :
a) Tại điểm
b) Tại điểm có hoành độ bằng ;
c) Biết rằng hệ số góc của tiếp tuyến bằng -.
-
Bài tập Mặt phẳng vuông góc - Toán 11
I. Bài tập trắc nghiệm
Bài 1: Cho tứ diện ABCD có: AB = AC = AD, góc bằng góc bằng 600. Gọi M và N lần lượt là trung điểm của AB và CD.
a) Góc giữa hai mặt phẳng (ACD) và (BCD) là:
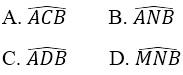
b) Mặt phẳng (BCD) vuông góc với mặt phẳng
A. (CDM)
B. (ACD)
C. (ABN)
D. (ABC)
c) Đường vuông góc chung của AB và CD là:
A. BN
B. AN
C. BC
D. MN
Lời giải:
Đáp án: a- B, b - C, c - D
a. Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc là góc của hai mặt phẳng (ACD) và (BCD)
b. Ta có CD ⊥ (ABN) (do BN ⊥ CD và AN ⊥ CD) ⇒ (BCD) ⊥ (ABN)
c. CD ⊥ MN; AB ⊥ (CDM) (do AB ⊥ CM và AB ⊥ DM)
MN là đường vuông góc chung của AB và CD
Bài 2: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.
a) Khằng định nào sau đây đúng?
A. AB ⊥ (ACD).
B. BC ⊥ (ACD).
C. CD ⊥ (ABC).
D. AD ⊥ (BCD).
b) Điểm cách đều bốn điểm A, B, C, D là:
A. trung điểm J của AB
B. trung điểm I của BC
C. trung điểm K của AD
D. trung điểm M của CD
Lời giải:
Đáp án: a - C, b - C
a. Phương án A sai vì chỉ có AB ⊥ CD; phương án B sai vì chỉ có : BC ⊥ CD
Phương án C đúng vì
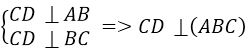
Phương án D sai vì AD không vuông góc với đường thẳng nào thuộc mặt phẳng (BCD)
b. CD ⊥ (ABC) vì CD ⊥ AB và CD ⊥ BC
AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C
Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của BC không cách đều ba điểm A, B, C
Phương án C đúng vì tam giác ACD vuông góc tại C nên trung điểm K của AD cách đều ba điểm A, C, D; tam giác ABD vuông góc tại B nên trung điểm K của AD cách đều ba điểm A, B và D
Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D
Bài 3: Cho chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.
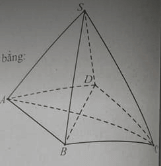
a) Đường thẳng SA vuông góc với
A. SC
B. SB
C. SD
D. CD
b) Khoảng cách từ D đến mặt phẳng (SAC) bằng:

Lời giải:
Đáp án: a - A, b - D
a. Tứ giác ABCD là hình vuông nên 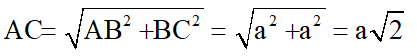
Tam giác SAC có SA = a, SC = a và AC = ⇒ SAC là tam giác vuông tại S, hay SA ⊥ SC
b. Gọi O là giao của AC và BD ⇒ DO ⊥ (SAC) (do DO ⊥ AC và DO ⊥ SO)
⇒ khoảng cách từ D đến (SAC) bằng DO
Ta có: 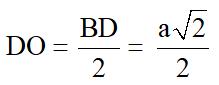
Bài 4: Cho hình lập phương ABCD.A’B’C’D’:
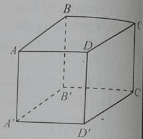
a) Mặt phẳng (ACC’A’) không vuông góc với mp nào?
b) Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là?
Lời giải:
a) Ta có: 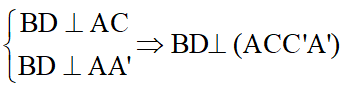
*Vì 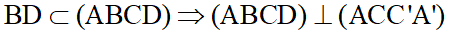
*Vì 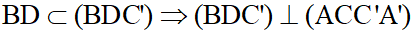
*Vì 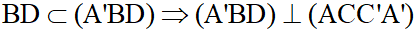
Vậy mp(CDD’C’) không vuông góc với mặt phẳng (ACC’A’).
b) Ta có: BD = A’B = A’D nên tam giác A’BD là tam giác đều.
Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.
Bài 5: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.
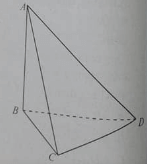
a) Đường thẳng AB vuông góc với mp nào?
b) Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?
A. Không vuông góc với mặt nào?
B. (ACD) C. (ABC) D. (BCD)
c) Đường vuông góc chung của AB và CD là:
A. AC
B. BC
C. AD
D. BD
Lời giải:
Đáp án: a - A, b - D, c - B
a. AB ⊥ CD và AB ⊥ CD ⇒ AB ⊥ (BCD)
b. vì AB ⊥ (BCD) ⇒ (ABD) ⊥ (BCD)
c. BC ⊥ AB và BC ⊥ CD ⇒ BC là đường vuông góc chung của AB và CD
Bài 6: Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
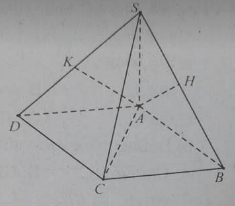
a) Hai mặt phẳng (SAB) và (SBC) vuông góc vì.
A. Góc của (SAB) và (SBC) là góc ABC và bằng 900.
B. Góc của (SAB) và (SBC) là góc BAD và bằng 900.
C. AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC)
D. BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA
b) Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
A. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD)
B. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK)
C. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK)
D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)
Lời giải:
Đáp án: a - D, b - B
a) Phương án A sai vì AB và CB không vuông góc với giao tuyến SB của (SAB) và (SBC), nên góc không phải là góc của hai mặt phẳng này;
Phương án B sai vì góc không phải là góc của hai mặt phẳng (SAB) với mặt phẳng (SBC);
Phương án C sai vì AB ⊥ BC thì chưa đủ để kết luận AB vuông góc với mặt phẳng (SBC);
Phương án D đúng vì : BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA ⇒ (SBC) ⊥ (SAB)
b) Phương án A sai vì hai điều kiện AH ⊥ (SBC) (do AH ⊥ SB và AH ⊥ BC) và AK ⊥ (SCD) (do AK vuông góc với SD và AK ⊥ CD) chưa liên quan đến (SAC); phương án B đúng vì AH ⊥(SBC) và AK ⊥ (SCD) nên SC ⊥ (AHK), từ đó suy ra hai mặt phẳng (AHK) và (SAC) vuông góc; phương án C và D đều sai vì chưa đủ điều kiện kết luận SC ⊥ (AHK)
Bài 7: Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc.
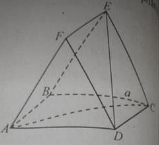
a) DE bằng:
A.
B.
C. 3a2
D. a(1 + )
b) Đường thẳng DE vuông góc
A. Chỉ với AC
B. Chỉ với BF
C. Chỉ với AC và BF
D. Hoặc với AC hoặc với BF
Lời giải:
Đáp án: a - A, b - C
EB ⊥(ABCD) vì nó vuông góc với giao tuyến AB của hai mặt phẳng vuông góc đã cho ⇒ CD ⊥ (EBC) ⇒ tam giác ECD vuông tại C.
⇒ DE = . Vậy phương án A đúng
Phương án C đúng vì : hình chiếu của DE lên (ABEF) là AE, mà AE ⊥ BF, suy ra DE ⊥ BF; hình chiếu của DE lên (ABCD) là BD, mà AC ⊥ BD, nên suy ra AC ⊥ DE.
Bài 8: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
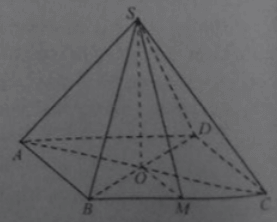
Tang của góc giữa mặt bên và mặt đáy bằng:
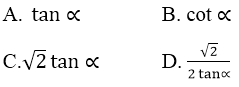
Bài 9: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng:
A. (SAD)
B. (SBD)
C. (SDC)
D. (SBC)
b) Giả sử góc BAD bằng 600. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng:
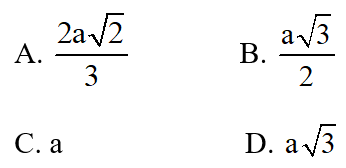
c) Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
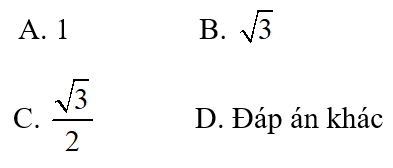
Lời giải:
Đáp án: a - B, b - A, c - D
a. Gọi I là giao điểm của AC và BD.
Từ S vẽ SO ⊥ (ABCD)
⇒ OA = OB = OC (là hình chiếu của các đường xiên bằng nhau)
⇒ O là tâm đường tròn ngoại tiếp tiếp tam giác ABC
Ta có: BI là đường trung tuyến của tam giác ABC nên O nằm trên đường thẳng BI hay 0 ∈ BD
Vậy SO ⊂ (SBD) và SO ⊥(ABCD) ⇒ (SBD) ⊥(ABCD)
b) Tam giác ABD có AB = AD và góc = 600 nên tam giác ABD đều suy ra: BD = a
Ta có; 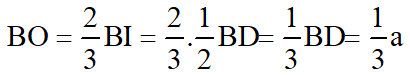
Tam giác SOB vuông tại O nên
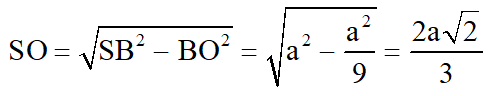
c. Từ O vẽ OM ⊥ BC ⇒ góc là góc của mặt bên và mặt phẳng đáy
Ta có: ABCD là hình thoi nên 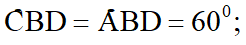
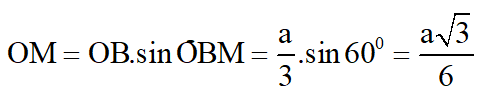
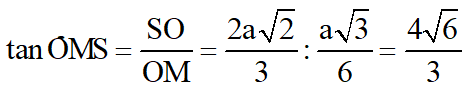
II. Bài tập tự luận có lời giải
Bài 1 Trong các mệnh đề sau đây, mệnh đề nào là đúng ?
a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song ;
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song ;
c) Mặt phẳng (α) vuông góc với đường thẳng b và b vuông góc với thẳng a, thì a song song với (α).
d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song.
e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.
Lời giải:
a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.
Bài 2 Trong các điều khẳng định sau đây, điều nào đúng?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Lời giải:
Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
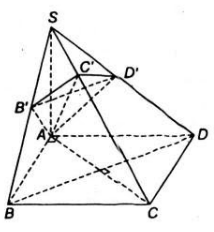
Bài 3 Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.
Lời giải:

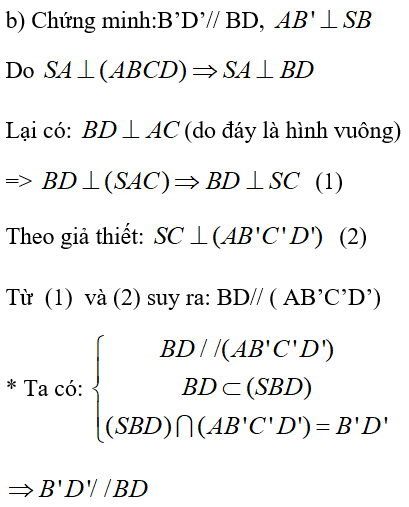
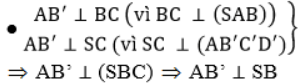
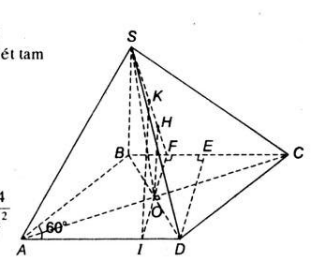
Bài 4 Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc BAD = 60o. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO = . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).
Lời giải:

Bài 5 Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB =a, AC =b. Tam giác ACD vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là các tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
Lời giải:
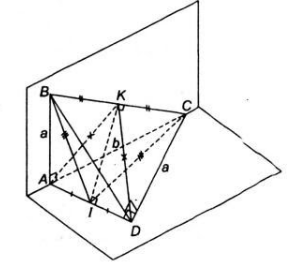


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.
Bài 6 Cho khối lập phương ABCD.A'B'C'D' cạnh a.
a) Chứng minh BC' vuông góc với mặt phẳng (A'B'CD)
b) Xác định và tính độ dài đoạn vuông góc chung của AB' và BC'.
Lời giải:
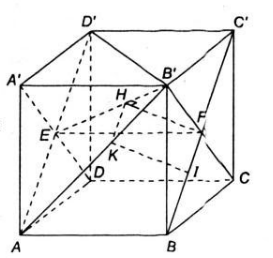

b) Do AD’ // BC’ nên mp(AB’D’) là mặt phẳng chứa AB’ và song song với BC’.
Ta tìm hình chiếu của BC’ trên mp ( AB’D’).
Gọi E và F lần lượt là tâm của các mặt bên ADD’A’ và BCB’C’.
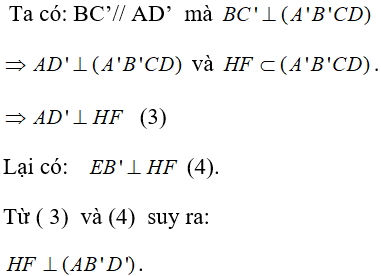
Vậy H là hình chiếu F trên mp (AB’D’). Qua H ta dựng đường thẳng song song với BC’ thì đường thẳng này chính là hình chiếu của BC’ trên mp(AB’D’).
Đường thẳng qua H song song với BC’ cắt AB’ tại K. Qua K kẻ đường thẳng song song với HF, đường này cắt BC’ tại I. Khi đó, KI chính là đường vuông góc chung của AB’ và BC’.
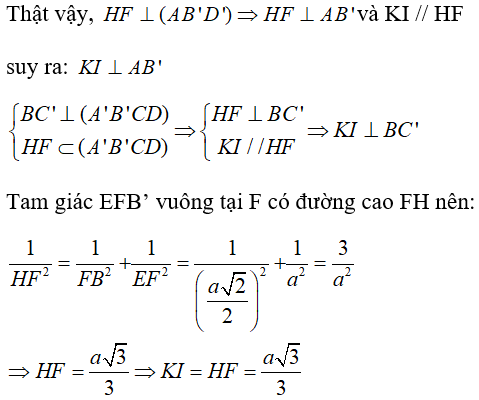
Bài 7 Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc = 60o và
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Lời giải:
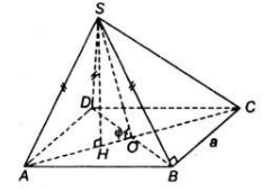
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc = 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
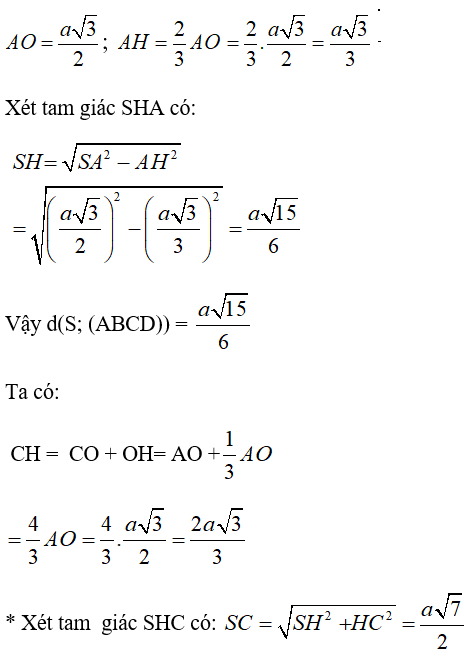

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích môn toán khác được cập nhật liên tục tại chuyên trang của chúng tôi.
Nhắc lại định nghĩa vectơ không gian.
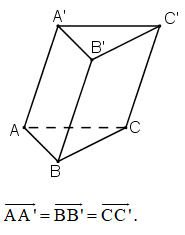
Bài 7 Cho hình lăng trụ tam giác ABC.A'B'C'. Hãy kể tên những vectơ bằng vectơ 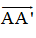 có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
Lời giải:
Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Bài 8 Trong không gian cho ba vectơ a , b và c đều khác vectơ . Khi nào ba véc tơ đó đồng phẳng?
Lời giải:
Ba vectơ đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:
- Giá của 3 vector đều cùng song song với mặt phẳng (P).
- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,
tức là tồn tại cặp số (m; n) duy nhất thỏa mãn 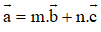
Bài 9 Trong không gian hai đường thẳng không cắt nhau có thể vuông góc với nhau không? Giả sử hai đường thẳng a và b lần lượt có vectơ chỉ phương là vector và vector . Khi nào ta có kết luận a và b vuông góc với nhau?
Lời giải:
+ Trong không gian, hai đường thẳng chéo nhau vẫn có thể vuông góc với nhau.
Đường thẳng a có vectơ chỉ phương
Đường thẳng b có vectơ chỉ phương
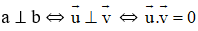
Bài 10 Muốn chứng minh đường thẳng a vuông góc với mặt phẳng (α) có cần chứng minh a vuông góc với mọi đường thẳng của (α) hay không?
Lời giải:
Không cần chứng minh a vuông góc với mọi đường thẳng của mặt phẳng.
Ta có thể chọn một trong số những cách sau để chứng minh đường thẳng vuông góc với mặt phẳng
- Cách 1 : Chứng minh đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng
- Cách 2 : Sử dụng định lí : "Nếu hai mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì cũng vuông góc với mặt phẳng kia".
- Cách 3 : Sử dụng định lí : " Nếu hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng cũng sẽ vuông góc với mặt phẳng đó"
III. Bài tập vận dụng
Bài 1 Cho ba mặt phẳng những mệnh đề nào sau đây đúng?
a) Nếu (α) ⊥ (β) và (α) // () thì (β) ⊥
b) Nếu (α) ⊥ (β) và (α) ⊥ thì (β) //
Bài 2 Cho hai mặt phẳng và vuông góc với nhau. Người ta lấy trên giao tuyến của hai mặt phẳng đó hai điểm và sao cho . Gọi là một điểm trên và là một điểm trên sao cho và cùng vuông góc với giao tuyến và , . Tính độ dài đoạn .
Bài 3 Trong mặt phẳng cho tam giác vuông ở . Một đoạn thẳng vuông góc với tại . Chứng minh rằng:
a) là góc giữa hai mặt phẳng và ;
b) Mặt phẳng vuông góc với mặt phẳng ;
c) với và lần lượt là giao điểm của và với mặt phẳng đi qua và vuông góc với .
Bài 4 Cho hai mặt phẳng , cắt nhau và một điểm không thuộc và không thuộc . Chứng minh rằng qua điểm có một và chỉ một mặt phẳng vuông góc với và . Nếu song song với thì kết quả trên sẽ thay đổi như thế nào?
Bài 5 Cho hình lập phương . Chứng minh rằng:
a) Mặt phẳng vuông góc với mặt phẳng ;
b) Đường thẳng vuông góc với mặt phẳng .
Bài 6 Cho hình chóp có đáy là một hình thoi cạnh và có . Chứng minh rằng:
a) Mặt phẳng vuông góc với mặt phẳng ;
b) Tam giác là tam giác vuông.
Bài 7 Cho hình hộp chữ nhật có .
a) Chứng minh rằng mặt phẳng vuông góc với mặt phẳng .
b) Tính độ dài đường chéo theo .
Bài 8 Tính độ dài đường chéo của một hình lập phương cạnh alpha.
Bài 9 Nhắc lại nội dung định lí ba đường thẳng vuông góc
Bài 10 Nhắc lại định nghĩa:
a) Góc giữa đường thẳng và mặt phẳng.
b) Góc giữa hai mặt phẳng.
Bài 11 Muốn chứng minh mặt phẳng (α) vuông góc với mặt phẳng (β) ta có thể ?
B. Đề thi tham khảo
Bộ đề thi Toán lớp 11 Học kì 2 năm 2022 - 2023
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Bộ đề thi Toán lớp 11 Học kì 2 năm 2022 - 2023 Đề số 1
I. PHẦN TRẮC NGHIỆM (5 điểm).
Câu 1 (TH). Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. Hai đường thẳng cùng song song với một mặt phẳng thì song song
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song
Câu 2 (TH). Hệ số góc k của tiếp tuyến với đồ thị hàm số tại giao điểm của đồ thị hàm số với trục tung là
A. k = 2
B. k = -2
C. k = 1
D. k = -1
Câu 3 (VD). Cho lăng trụ đứng có tất cả các cạnh đều bằng 2a. Khoảng cách giữa hai đường thẳng BC và AA' bằng
A.
B.
C.
D.
Câu 4 (TH). Cho hình lập phương có cạnh bằng a. Góc giữa hai đường thẳng CD' và A'C' bằng
A. 45o
B. 30o
C. 60o
D. 90o
Câu 5 (TH). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đường thẳng SA vuông góc với mặt phẳng đáy và góc giữa đường thẳng SC và mặt phẳng đáy bằng 30o. Gọi h là khoảng cách từ điểm S đến mặt phẳng (ABC) Mệnh đề nào dưới đây là đúng
A.
B.
C.
D.
Câu 6 (VD). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1, hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng đáy, SA = 1. Gọi M là trung điểm của cạnh SD. Khoảng cách từ điểm M đến mặt phẳng (SBC) bằng
A.
B.
C. 1
D.
Câu 7 (TH). Trong các giới hạn dưới đây, giới hạn nào là
A.
B.
C.
D.
Câu 8 (VD). Số các ước nguyên dương của 540 là
A. 24
B. 23
C. 12
D. 36
Câu 9 (TH). bằng
A.
B.
C.
D.
Câu 10 (VDC). Giá trị của tổng (tổng đó có 2018 số hạng) bằng
A.
B.
C.
D.
Câu 11 (TH). Một chuyển động có phương trình (trong đó s tính bằng mét, t tính bằng giây). Vận tốc tức thời của chuyển động tại thời điểm là
A. 6 (m/s)
B. 4 (m/s)
C. 8 (m/s)
D. 2 (m/s)
Câu 12 (VD). Một bình đựng 8 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi trong bình. Xác suất để có được ít nhất hai viên bi xanh là
A.
B.
C.
D.
Câu 13 (VD). Có bao nhiêu giá trị nguyên dương của x để ba số theo thứ tự đó lập thành một cấp số nhân?
A. 2
B. 3
C. 1
D. 0
Câu 14 (TH). Cho hàm số Tìm m để hàm số liên tục trên .
A. m = 4
B. m = -4
C. m = 1
D. m = 2
Câu 15 (TH). Cho với a, b là các số nguyên dương và là phân số tối giản. Tính tổng
A. 10
B. 5
C. 3
D. 4
Câu 16 (VD). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng Gọi là góc giữa mặt phẳng (SCD) và (ABCD) Mệnh đề nào dưới đây là đúng
A.
B.
C.
D.
Câu 17 (NB). Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 18 (VD). bằng
A. -1
B. 1
C.
D. -2018
Câu 19 (TH). Cho hàm số . Tính giá trị của biểu thức .
A.
B.
C.
D.
Câu 20 (VD). Cho hàm số với m là tham số thực. Số giá trị nguyên của m để với là
A. 1
B. 5
C. 4
D. 3
II. PHẦN TỰ LUẬN (5 điểm).
Câu 1 (3,5 điểm).
1) Tính các giới hạn
a)
b)
2) Tìm m để hàm số liên tục tại điểm x = -1.
Câu 2 (1,5 điểm). Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau.
1) Chứng minh đường thẳng OA vuông góc với đường thẳng BC.
2) Gọi lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Tìm giá trị lớn nhất của biểu thức .
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Bộ đề thi Toán lớp 11 Học kì 2 năm 2022 - 2023 Đề số 2
I. PHẦN TRẮC NGHIỆM
Câu 1 (NB). Đạo hàm cấp hai của hàm số là:
A. cosx
B. -cosx
C. sinx
D. -sinx
Câu 2 (TH). Giới hạn bằng:
A.
B.
C.
D.
Câu 3 (TH). Cho lăng trụ đứng ABC.A'B'C'. Mệnh đề nào sau đây sai?
A.
B. Các mặt bên của hình lăng trụ là các hình chữ nhật
C.
D.
Câu 4 (TH). Cho hình lập phương . Hệ thức nào sau đây đúng?
A.
B.
C.
D.
Câu 5 (VD). Cho hàm số . Tìm điểm M thuộc đồ thị hàm số biết tiếp tuyến của đồ thị hàm số tại điểm M có hệ số góc nhỏ nhất.
A.
B.
C.
D.
Câu 6 (TH). Cho hàm số .Tập nghiệm của bất phương trình là:
A.
B.
C.
D.
Câu 7 (TH). Với giá trị nào của m thì hàm số liên tục trên ?
A.
B. 4
C. 3
D. 1
Câu 8 (VD). Giới hạn bằng:
A.
B.
C. 0
D.
Câu 9 (TH). Cho hàm số . Tính
A. 5
B. 3
C.
D. 4
Câu 10 (TH). Cho hình chóp S.ABC có . Gọi H là hình chiếu vuông góc của A trên BC. Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Câu 11 (TH). Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA vuông góc với đáy. Khi đó số mặt bên của hình chóp là tam giác vuông bằng:
A. 4
B. 1
C. 2
D. 3
Câu 12 (TH). Giới hạn bằng:
A.
B.
C. 1
D. -4
Câu 13 (TH). Đạo hàm của hàm số là:
A.
B.
C.
D.
Câu 14 (TH). Cho hàm số . Tính
A. 1
B. 2
C. -1
D. -2
Câu 15 (TH). Cho hàm số . Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 0 là:
A.
B.
C.
D.
Câu 16 (VD). Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:
A. 60o
B. 90o
C. 45o
D. 30o
Câu 17 (TH). Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu và thì
B. Qua một điểm có vô số đường thẳng vuông góc với một mặt phẳng cho trước.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Câu 18 (TH). Trong các giới hạn sau, giới hạn nào bằng 0?
A.
B.
C.
D.
Câu 19 (VD). Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Tan của góc giữa mặt bên và mặt đáy bằng:
A.
B.
C.
D.
Câu 20 (TH). Tổng của cấp số nhân lùi vô hạn với số hạng đầu bằng 2 và công bội bằng:
A.
B.
C.
D.
II. PHẦN TỰ LUẬN (5 điểm)
Câu 1 (VD). Tính
Câu 2 (VD). Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến đó đi qua điểm A(0; 2).
Câu 3 (VD). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnH 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng
a) Chứng minh tam giác SBC vuông.
b) Tính góc giữa mặt bên (SCD) và mặt đáy (ABCD).
c) Tính khoảng cách từ điểm B đến mặt phẳng
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng học kì 2
Năm học 2022 - 2023
Môn: Toán 11
Thời gian làm bài: 45 phút
Bộ đề thi Toán lớp 11 Học kì 2 năm 2022 - 2023 Đề số 3
A. PHẦN TRẮC NGHIỆM (30 câu; 6,0 điểm)
Câu 1 (TH). Đạo hàm của hàm số bằng
A.
B.
C.
D.
Câu 2 (TH). Hàm số nào sau đây có đạo hàm bằng
A.
B.
C.
D.
Câu 3 (TH). Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng Mệnh đề nào sau đây đúng?
A. Nếu thì a và b cắt nhau hoặc chéo nhau a // mp(P)
B. Nếu và thì a // mp(P)
C. Nếu và thì a//b
D. Nếu và thì
Câu 4 (VD).Tính giới hạn ta được kết quả là:
A. 4
B. 2
C. 3
D. 1
Câu 5 (TH). Trong không gian, cho hai đường thẳng a và b chéo nhau. Mệnh đề nào sai đây SAI?
A. Tồn tại một mặt phẳng chứa a và song song với b.
B. Khoảng cách giữa a và b bằng độ dài đường vuông góc chung của a và b.
C. Tồn tại duy nhất một cặp mặt phẳng lần lượt chứa 2 đường thẳng a, b và song song với nhau.
D. Tồn tại một mặt phẳng chứa b và song song với a.
Câu 6 (TH).Trong không gian, cho đường thẳng a và mặt phẳng (P). Có bao nhiêu mặt phẳng chứa đường thẳng a và vuông góc với mặt phẳng (P).
A. Có duy nhất một
B. Có vô số
C. Có một hoặc vô số
D. Không có
Câu 7 (TH).Cho hàm số . Tìm x để
A. x > 0
B. x < 0
C. x < - 1
D. -1 < x < 0
Câu 8 (TH).Tính giới hạn ta được kết quả là:
A. 1
B. 2
C. 3
D. 4
Câu 9 (TH). Giới hạn bằng
A.
B.
C. 0
D. 1
Câu 10 (TH). Tính giới hạn ta được kết quả là:
A. 4
B.
C. 0
D. 2
Câu 11 (VD). Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a; cạnh bên SA vuông góc với mặt đáy, gọi M là trung điểm AC. Tính khoảng cách từ M đến mp(SBC).
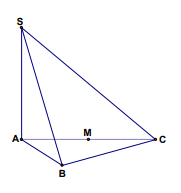
A.
B.
C.
D.
Câu 12 (TH). Cho các hàm số có đạo hàm trên khoảng J và với mọi . Mệnh đề nào sau đây SAI?
A.
B.
C.
D.
Câu 13 (VD). Cho hình chóp S.ABC, tam giác ABC vuông tại B, cạnh bên SA vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SB. Mệnh đề nào sau đây SAI?
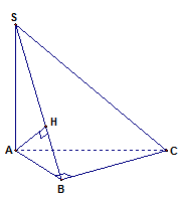
A. Các mặt bên của hình chóp là các tam giác vuông
B. AH // BC
C. AH SC
D. vuông
Câu 14 (VD). Cho hàm số có đồ thị (C) và điểm A(m; 1). Gọi S là tập các giá trị của m để có đúng một tiếp tuyến (C) của đi qua A. Tính tổng bình phương các phần tử của tập S.
A.
B.
C.
D.
Câu 15 (VD). Biết hàm số liên tục tại x = 1. Tính giá trị của biểu thức P = a - 4b
A. P = 4
B. P = -4
C. P = -5
D. P = 5
Câu 16 (TH). Cho hình lăng trụ ABC.A'B'C' đều. Mệnh đề nào sau đây SAI?
A. Lăng trụ đã cho là lăng trụ đứng
B. Các mặt bên của lăng trụ là hình chữ nhật
C. Hai mặt đáy của lăng trụ là các đa giác đều
D. Tam giác B'AC đều
Câu 17 (VD). Phương trình có nghiệm thuộc khoảng nào sau đây?
A.
B.
C.
D.
Câu 18 (TH). Cho hàm số . Ta có bằng
A.
B.
C.
D.
Câu 19 (TH). Cho hàm số Mệnh đề nào sau đây ĐÚNG?
A. Hàm số liên tục tại x = 1
B. Hàm số không liên tục tại các điểm x =1
C. Hàm số liên tục tại mọi
D. Hàm số liên tục tại
Câu 20 (TH). Cho hàm số , tiếp tuyến với đồ thị của hàm số tại điểm có phương trình là:
A.
B.
C.
D.
Câu 21 (TH). Cho hàm số , tiếp tuyến song song với đường thẳng của đồ thị hàm số là:
A. và
B.
C.
D.
Câu 22 (TH). Mệnh đề nào sau đây SAI?
A.
B.
C.
D.
Câu 23 (TH). Trong không gian, mệnh đề nào sau đây ĐÚNG?
A. Côsin của góc giữa hai đường thẳng trong không gian có thể là một số âm.
B. Góc giữa hai đường thẳng thuộc khoảng
C. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
D. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và một đường thẳng nằm trong mặt phẳng đó.
Câu 24 (VD). Tìm m để hàm số liên tục tại x =1.
A. m = 0
B. m = -1
C. m = 2
D. m = 1
Câu 25 (TH). Trong không gian cho m (P) và điểm M không thuộc mp (P). Mệnh đề nào sau đây ĐÚNG?
A. Qua M kẻ được vô số đường thẳng vuông góc với mp (P).
B. Qua M có vô số đường thẳng song song với mp(P)và các đường thẳng đó cùng thuộc mặt phẳng (Q) qua M và song song với (P)
C. Qua M có duy nhất một mặt phẳng vuông góc với mp (P).
D. Có duy nhất một đường thẳng đi qua M tạo với mp (P) một góc bằng 60o.
Câu 26 (VD). Cho tứ diện ABCD đều, gọi G là trọng tâm tam giác BCD. Mệnh đề nào sau đây SAI?
A.
B.
C.
D.
Câu 27 (VD). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy, SA = 2a. Mệnh đề nào sau đây SAI?
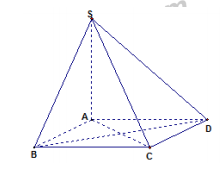
A.
B. Tam giác SBD cân
C.
D.
Câu 28 (VD). Giới hạn bằng
A.
B. 0
C.
D.
Câu 29 (VD). Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với mặt đáy, Gọi là góc giữa SB và mp(SAC), tính ?
A.
B.
C.
D. Đáp án khác
Câu 30 (VD). Cho hình chóp S.ABC có đáy ABC vuông cân tại tam giác SBC đều nằm trong mặt phẳng vuông góc với mặt đáy. Tính khoảng cách giữa hai đường thẳng AC và SB ta được kết quả là:
A.
B.
C.
D.
II. PHẦN TỰ LUẬN (2 câu; 4,0 điểm)
Bài 1 (TH) (2,5 điểm).
1. Cho hàm số có đồ thị (C)
a) Tính y''(1)
b) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm M có hoành độ x = 1.
2. Cho hàm số Xét tính liên tục của hàm số tại x = 2.
Bài 2 (VD) (1,5 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a; hình chiếu vuông góc của S trên mặt đáy là trung điểm H của OA; góc giữa mặt phẳng (SCD) và mặt đáy bằng 45o.
1. Chứng minh .
2. Tính khoảng cách từ B đến mặt phẳng (SCD).
Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:
Hệ thống kiến thức Toán lớp 11 Giữa học kì 2
TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án
Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất
Các dạng bài tập Toán lớp 11 Học kì 2
Hệ thống kiến thức Toán lớp 11 Học kì 2




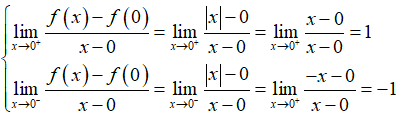
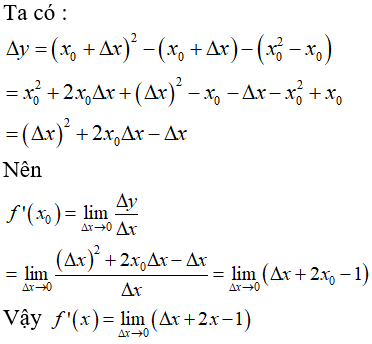
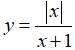 liên tục tại x= 0. (2) Hàm số
liên tục tại x= 0. (2) Hàm số 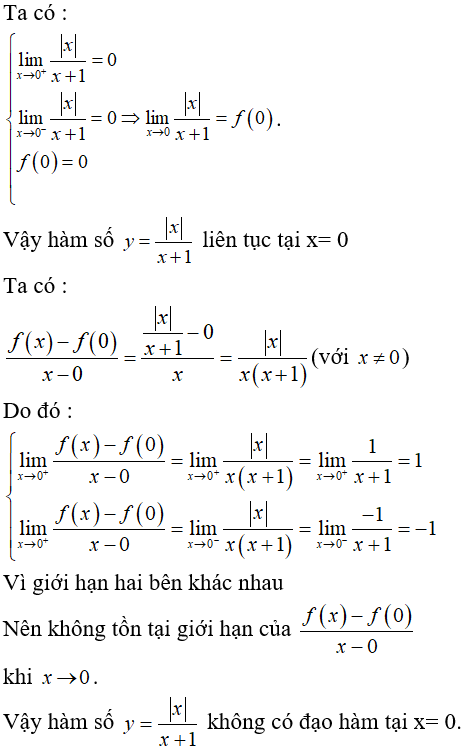
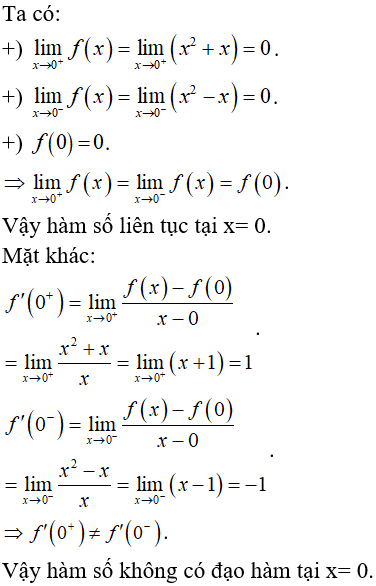
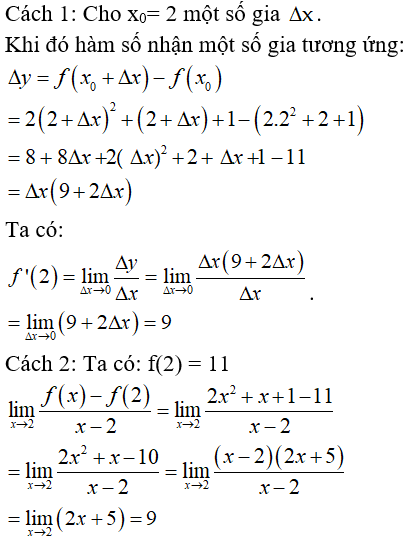
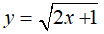 tại x0 = 1
tại x0 = 1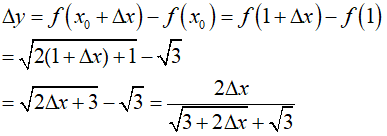
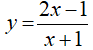 tại x = 3
tại x = 3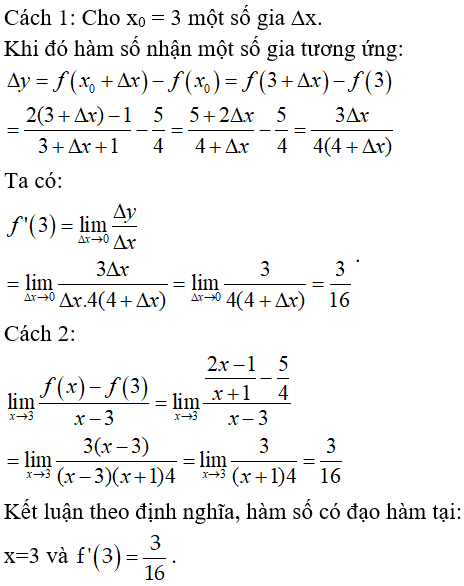
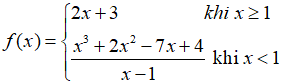 tại x0 = 1.
tại x0 = 1.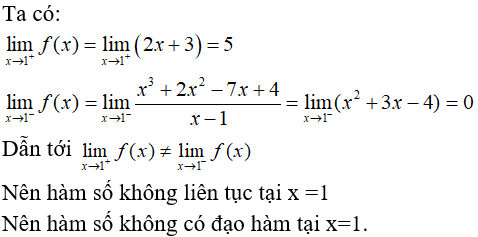
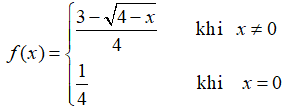 . Khi đó f'(0) là kết quả nào sau đây?
. Khi đó f'(0) là kết quả nào sau đây?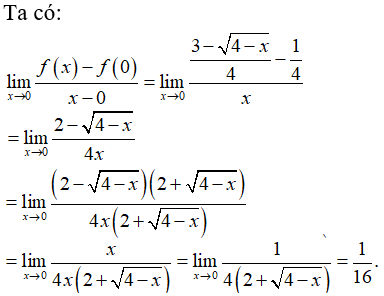
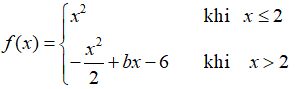 . Để hàm số này có đạo hàm tại x = 2 thì giá trị của b là
. Để hàm số này có đạo hàm tại x = 2 thì giá trị của b là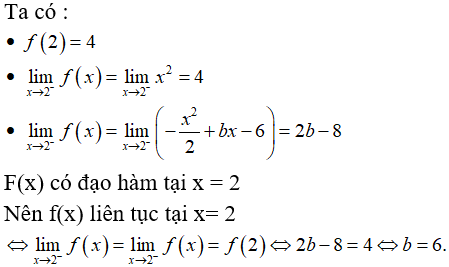

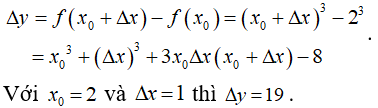
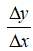 của hàm số f(x) = 2x.( x - 1) theo x và Δx là?
của hàm số f(x) = 2x.( x - 1) theo x và Δx là?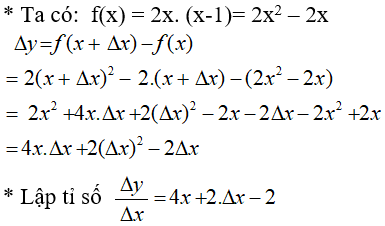
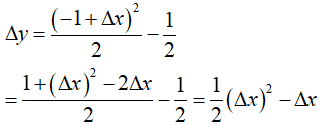
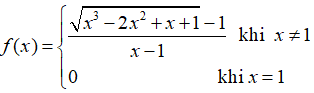 tại điểm x0 = 1.
tại điểm x0 = 1.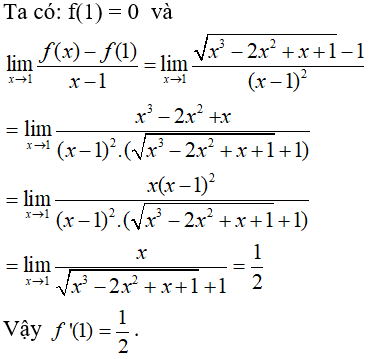
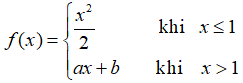 . Với giá trị nào sau đây của a, b thì hàm số có đạo hàm tại x = 1?
. Với giá trị nào sau đây của a, b thì hàm số có đạo hàm tại x = 1?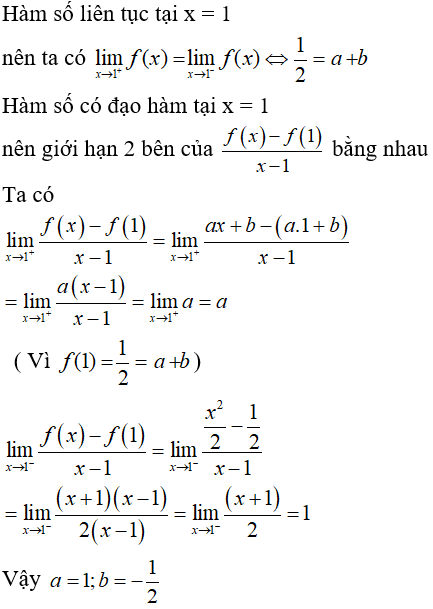
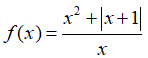 tại x = 1.
tại x = 1.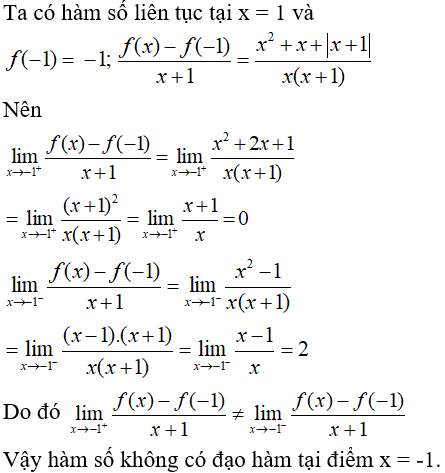


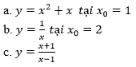
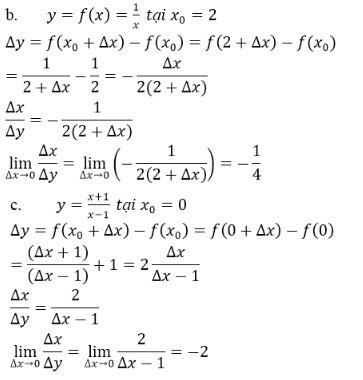
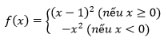

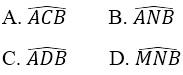
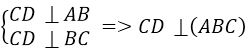


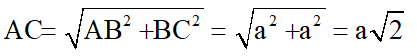
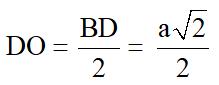

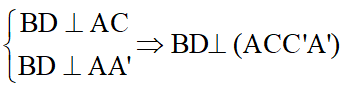
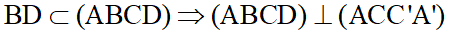
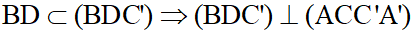
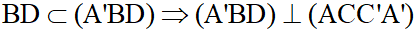




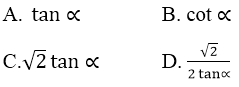
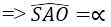
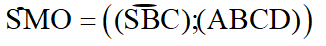
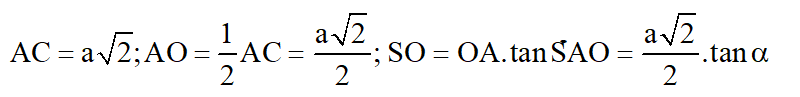
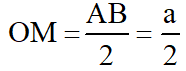
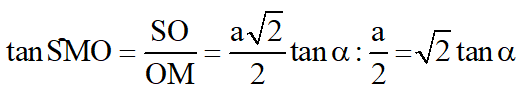
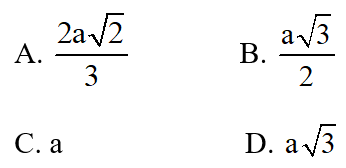
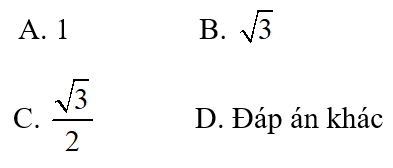
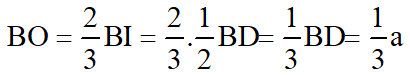
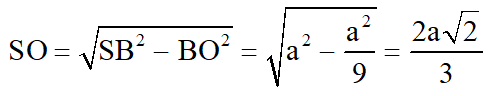
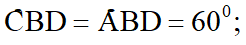
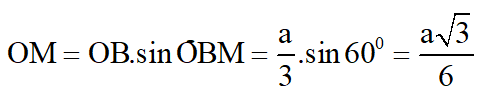
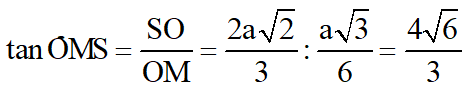


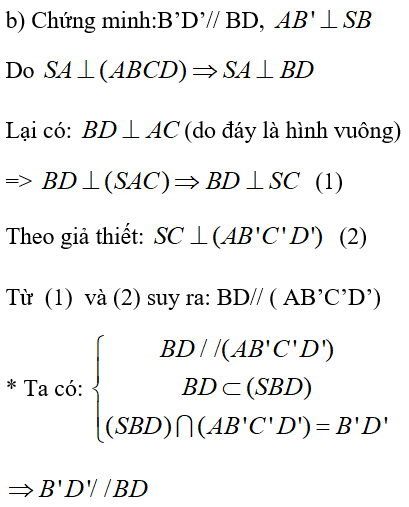
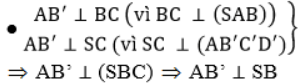







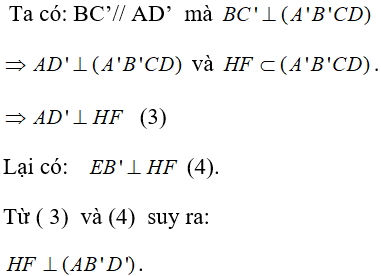
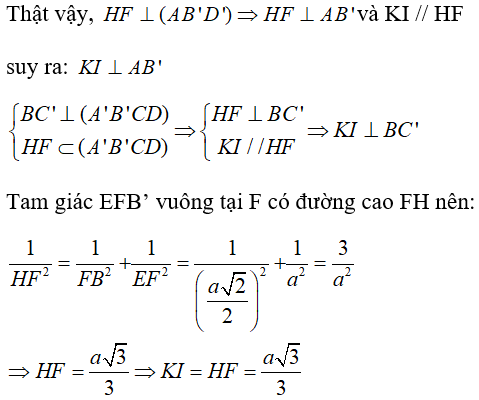

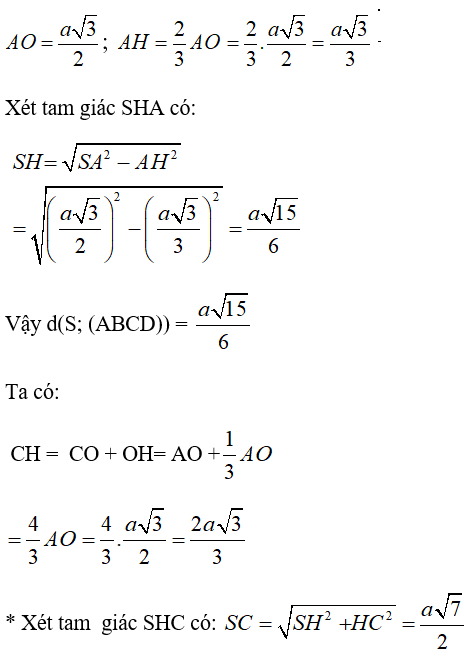

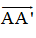 có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.