Các dạng bài tập Toán lớp 11 Học kì 2
Tổng hợp các dạng bài tập Toán lớp 11 Học kì 2 gồm các dạng Toán từ cơ bản đến nâng cao với phương pháp giải chi tiết giúp học sinh nắm vững kiến thức từ đó biết cách giải bài tập Toán 11.
Các dạng bài tập Toán lớp 11 Học kì 2
A. ĐẠI SỐ VÀ GIẢI TÍCH
50 bài tập về Giới hạn của dãy số (có đáp án 2022) – Toán 11
50 bài tập về Giới hạn của hàm số (có đáp án 2022) – Toán 11
50 bài tập về Hàm số liên tục (có đáp án 2022) – Toán 11
50 bài tập về Cách tính đạo hàm bằng định nghĩa hay (có đáp án 2022)– Toán 11
50 bài tập về Quy tắc tính đạo hàm (có đáp án 2022) – Toán 11
50 bài tập về Đạo hàm của hàm số lượng giác (có đáp án 2022) – Toán 11
50 bài tập về Ứng dụng Đạo hàm để giải phương trình, bất phương trình (có đáp án 2022) – Toán 11
50 bài tập về Các dạng bài tập về tiếp tuyến lớp 11 (có đáp án 2022) – Toán 11
B. HÌNH HỌC
Các dạng bài tập Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
50 bài tập về Đại cương về đường thẳng (có đáp án 2022) – Toán 11
50 bài tập về Hai đường thẳng song song trong không gian (có đáp án 2022) – Toán 11
50 bài tập về Đường thẳng và mặt phẳng song song (có đáp án 2022) – Toán 11
50 bài tập về Hai mặt phẳng song song (có đáp án 2022) – Toán 11
Công thức Giao tuyến của ba mặt phẳng và hệ quả
Công thức Chứng minh hai đường thẳng song song trong không gian
Công thức Chứng minh đường thẳng song song với mặt phẳng
Công thức Chứng minh hai mặt phẳng song song
50 bài tập về Định lý Ta-lét trong không gian đầy đủ (có đáp án 2022) - Toán 11
1. Lý thuyết
a) Định nghĩa đạo hàm
- Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0∈(a;b). Giới hạn hữu hạn (nếu có) của tỉ số f(x)−f(x0)x−x0 khi x→x0 được gọi là đạo hàm của hàm số đã cho tại x0.
- Kí hiệu là f’(x0) hay y’(x0). Như vậy ta có: f'.
- Nhận xét:
Nếu đặt và thì ta có .
Trong đó được gọi là số gia của biến số tại x0
gọi là số gia của hàm số ứng với số gia tại x0.
b) Đạo hàm một bên
- Đạo hàm bên trái của hàm số y = f(x) tại điểm x0, kí hiệu là được định nghĩa là:
trong đó được hiểu là và x < x0.
- Đạo hàm bên phải của hàm số y = f(x) tại điểm x0, kí hiệu là được định nghĩa là:
trong đó được hiểu là và x > x0.
- Định lí: Hàm số y = f(x) có đạo hàm tại điểm x0 thuộc tập xác định của nó, nếu và chỉ nếu và tồn tại và bằng nhau. Khi đó ta có: .
c) Đạo hàm trên khoảng, trên đoạn
- Hàm số y = f(x) có đạo hàm (hay hàm khả vi) trên (a; b) nếu nó có đạo hàm tại mọi điểm thuộc (a; b).
- Hàm số y = f(x) có đạo hàm (hay hàm khả vi) trên [a; b] nếu nó có đạo hàm tại mọi điểm thuộc (a; b) đồng thời tồn tại đạo hàm trái f’(b -) và đạo hàm phải f’(a+) .
d) Quy tắc tính đạo hàm bằng định nghĩa
Muốn tính đạo hàm của hàm số tại điểm x0 theo định nghĩa, ta có 2 cách:
- Cách 1:
Bước 1: Với là số gia của đối số tại x0 ta tính
Bước 2: Tính giới hạn .
- Cách 2: Đạo hàm của hàm số tại x0 là
e) Mối liên hệ giữa đạo hàm và tính liên tục
Định lí: Nếu hàm số f(x) có đạo hàm tại x0 thì f(x) liên tục tại x0.
Chú ý: Định lí trên chỉ là điều kiện cần, tức là một hàm có thể liên tục tại điểm x0 nhưng hàm đó không có đạo hàm tại x0.
2. Các dạng bài tập
Dạng 1: Tìm số gia của hàm số
Phương pháp giải:
Để tính số gia của hàm số y = f(x) tại điểm x0 tương ứng với số gia cho trước ta áp dụng công thức: .
Ví dụ minh họa:
Ví dụ 1: Tìm số gia của hàm số y = f(x) = x3 – 3x2 + 2, biết rằng:
a)
b) .
Lời giải
a) Số gia của hàm số là:
.
b) Số gia của hàm số là:
.
Ví dụ 2: Tìm số gia của hàm số:
a) y = 2x + 3
b) y = 2x2 – 3x + 1 tại x0 = 1
Lời giải
a) Số gia của hàm số là:
b) Số gia của hàm số là:
.
Dạng 2: Tính đạo hàm bằng định nghĩa
Phương pháp giải:
Muốn tính đạo hàm của hàm số tại điểm x0 theo định nghĩa, ta có 2 cách:
Cách 1:
Bước 1: Với là số gia của đối số tại x0 ta tính
Bước 2: Tính giới hạn .
Cách 2: Đạo hàm của hàm số tại x0 là
Chú ý: Nếu không tồn tại giới hạn hữu hạn tại x0 thì hàm số không có đạo hàm tại x0.
Ví dụ minh họa:
Ví dụ 1: Tính đạo hàm (bằng định nghĩa) của các hàm số sau:
a) y = 2x2 + x + 1 tại x0 = 2.
b) tại x0 = 1.
c) tại x0 = 3
Lời giải
a) Cách 1: Với là số gia của đối số x0 = 2.
Khi đó hàm số số gia tương ứng:
Ta có .
Cách 2:
.
Kết luận theo định nghĩa, hàm số có đạo hàm tại và .
b) Cách 1: Với là số gia của đối số x0 = 1.
Khi đó hàm số số gia tương ứng:
Ta có .
Cách 2: .
Kết luận theo định nghĩa, hàm số có đạo hàm tại x0 = 1 và
c) Cách 1: Với là số gia của đối số x0 = 3.
Khi đó hàm số số gia tương ứng:
Ta có .
Cách 2:
.
Kết luận theo định nghĩa, hàm số có đạo hàm tại x0 = 3 và .
Ví dụ 2: Tính đạo hàm (bằng định nghĩa) của các hàm số sau:
a) y = x3 tại x0
b) tại x0
Lời giải
a) Với là số gia của đối số x0.
Khi đó hàm số số gia tương ứng:
Ta có:
Vậy đạo hàm của hàm số tại x0 là
b) Với là số gia của đối số x0.
Khi đó hàm số số gia tương ứng:
Ta có:
Dạng 3: Mối liên hệ giữa đạo hàm và tính liên tục của hàm số
Phương pháp giải:
Định lí: Nếu hàm số f(x) có đạo hàm tại x0 thì f(x) liên tục tại x0.
Chú ý: Nếu hàm số không liên tục tại x0 thì không có đạo hàm tại x0.
Ví dụ minh họa:
Ví dụ 1: Hàm số y = f(x) = |x| liên tục tại x = 0 nhưng không tồn tại đạo hàm tại x = 0:
Lời giải
Ta có: nên hàm số f(x) = |x| liên tục tại x = 0.
Ta có:
Nên nên hàm số không có đạo hàm tại x = 0.
3. Bài tập tự luyện
Câu 1. Số gia của hàm số ứng với số gia của đối số x tại x0 = – 1 là
A.
B.
C.
D.
Câu 2. Tỉ số của hàm số f(x) = 2x(x – 1) theo x và là
A.
B.
C.
D.
Câu 3. Số gia của hàm số f(x) = x3 ứng với x0 = 2 và bằng bao nhiêu?
A. – 19 .
B. 7 .
C. 19.
D. –7.
Câu 4. Tính tỷ số của hàm số theo x và
A.
B.
C.
D.
Câu 5. Đạo hàm của hàm số f(x) = 2x + 1 tại x0 = 1
A. 2
B. 3
C. 4
D. 5
Câu 6. Đạo hàm của hàm số f(x) = x3 tại x0 = 1
A. 4
B. 3
C. 5
D. 6
Câu 7. Đạo hàm của hàm số y = x3 + x – 2 tại x0 = – 2 là
A. 13.
B. 12.
C. 10.
D. – 8.
Câu 8. Đạo hàm của hàm số tại điểm x0 = 2
A.
B.
C.
D.
Câu 9. Đạo hàm của hàm số tại x0 = 2 là
A. .
B. .
C. .
D. .
Câu 10. Đạo hàm của hàm số tại x0 = 1 là
A. 15.
B. – 15.
C. – 17.
D. 17.
Câu 11. Đạo hàm của hàm số tại x0 = – 1.
A. 2
B. 0
C. 3
D. Đáp án khác
Câu 12. Đạo hàm của hàm số f(x) = x2 – x tại điểm x0 ứng với số gia là:
A.
B.
C.
D.
Câu 13. Cho hàm số . Khẳng định nào là đúng:
A. Hàm số liên tục trên R, không có đạo hàm trên R.
B. Hàm số liên tục trên R, có đạo hàm trên R.
C. Hàm số không liên tục trên R, không có đạo hàm trên R.
D. Hàm số không liên tục trên R, có đạo hàm trên R.
Câu 14. Cho hàm số y = |2x – 3|. Khẳng định nào là đúng:
A. Hàm số liên tục tại , không có đạo hàm tại .
B. Hàm số liên tục tại , có đạo hàm tại .
C. Hàm số không liên tục tại , không có đạo hàm tại .
D. Hàm số không liên tục tại , có đạo hàm tại .
Câu 15. Cho hàm số y = f(x) =x2 - 2|x + 3|. Khẳng định nào là đúng:
A. Hàm số liên tục trên R, không có đạo hàm trên R.
B. Hàm số liên tục trên R, có đạo hàm trên R.
C. Hàm số không liên tục trên R, không có đạo hàm trên R.
D. Hàm số không liên tục trên R, có đạo hàm trên R.
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
A |
C |
C |
B |
A |
B |
A |
B |
B |
D |
D |
A |
C |
A |
A |
Công thức Chứng minh hai đường thẳng song song trong không gian - Toán lớp 11
1. Lý thuyết
a) Vị trí tương đối của hai đường thẳng trong không gian
Cho hai đường thẳng a và b trong không gian. Khi đó có thể xảy ra một trong các trường hợp sau:
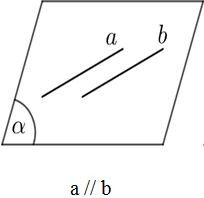
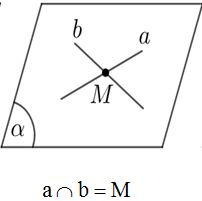
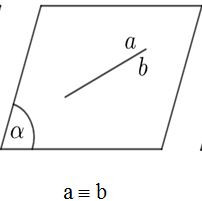
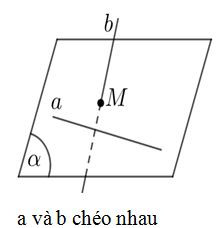
b) Tính chất
Định lý 1:
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
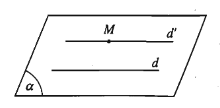
Định lý 2:
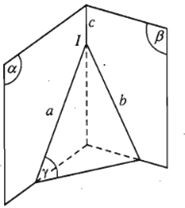
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
Tức là:
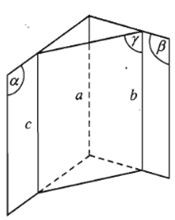
Hệ quả (của định lý 2):
Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của hai mặt phẳng đó (nếu có) cũng song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).
Tức là:
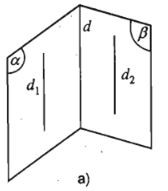
Định lý 3:
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.
Tức là:
2. Công thức
Phương pháp chứng minh hai đường thẳng song song trong không gian
- Cách 1: Chứng minh chúng đồng phằng, sau đó áp dụng phương pháp chứng minh song song trong hình học phẳng:
Sử dụng tính chất đường trung bình, Định lý Ta-lét đảo, cùng vuông góc với đường thẳng thứ ba.
- Cách 2: Chứng minh hai đường thẳng đó cùng song song với đường thẳng thứ ba
- Cách 3: Áp dụng định lý giao tuyến song song
3. Ví dụ minh họa
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng IJ // AB, từ đó suy ra IJ // CD.
Lời giải
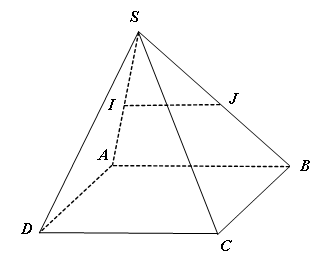
+ Xét tam giác SAB có I, J lần lượt là trung điểm của các cạnh SA, SB
Nên IJ là đường trung bình của tam giác SAB.
Từ đó suy ra IJ // AB.
+ Ta có
Ví dụ 2: Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho ; I, J lần lượt là trung điểm của BD, CD.
a) Chứng minh rằng MN // BC.
b) Tứ giác MNJI là hình gì. Tìm điều kiện của M, N để tứ giác MNJI là hình bình hành.
Lời giải
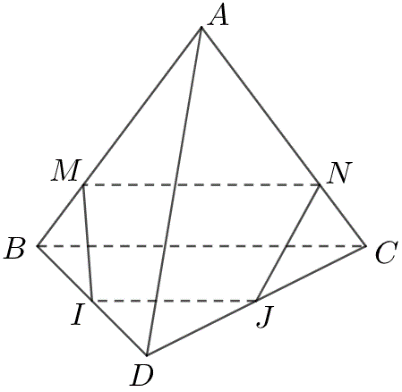
a) Xét tam giác ABC có: , từ đó suy ra MN // BC (Định lý Ta-lét đảo).
b) + Xét tam giác BCD có I, J lần lượt là trung điểm của BD, CD
Nên IJ là đường trung bình của tam giác BCD.
Từ đó suy ra IJ // BC và
+ Ta có:
Vậy tứ giác MNJI là hình thang.
+ Để hình thang MNJI là hình bình hành thì
Xét tam giác ABC có MN // BC nên
Do đó M, N lần lượt là trung điểm của AB, AC.
4. Bài tập tự luyện
Câu 1. Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Chọn khẳng định đúng trong các khẳng định sau?
A. IJ song song với CD.
B. IJ song song với AB.
C. IJ chéo CD.
D. IJ cắt AB.
Câu 2. Cho hình chóp S.ABCD có AD không song song với BC. Gọi M, N, P, Q, R, T lần lượt là trung điểm AC, BD, BC, CD, SA, SD. Cặp đường thẳng nào sau đây song song với nhau?
A. MP và RT.
B. MQ và RT.
C. MN và RT.
D. PQ và RT.
Đáp án: 1A, 2B.
Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:
Hệ thống kiến thức Toán lớp 11 Giữa học kì 2
TOP 30 Đề thi Toán Học kì 2 lớp 11 năm 2022 - 2023 có đáp án
Đề cương Học kì 2 Toán lớp 11 năm 2022 - 2023 chi tiết nhất
