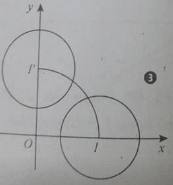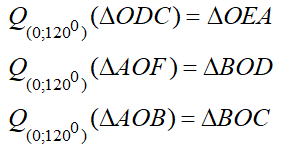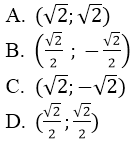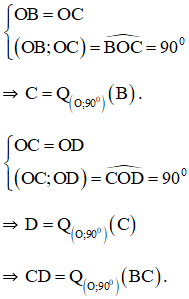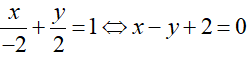Bài tập Toán lớp 11 Giữa học kì 1 có đáp án

Nếu chọn một học sinh nam có 280 cách.

Nếu chọn một học sinh nữ có 325 cách.

Theo qui tắc cộng, ta có 280 + 325 = 605 cách chọn.

Chọn đáp án D

Vì các quả cầu trắng hoặc đen đều được đánh số phân biệt nên mỗi lần lấy ra một quả cầu bất kì là một lần chọn.

Nếu chọn một quả trắng có 6 cách.

Nếu chọn một quả đen có 3 cách.

Theo qui tắc cộng, ta có 6 + 3 = 9 cách chọn.

Chọn đáp án B

Nếu đi bằng ô tô có 10 cách.

Nếu đi bằng tàu hỏa có 5 cách.

Nếu đi bằng tàu thủy có 3 cách.

Nếu đi bằng máy bay có 2 cách.

Theo qui tắc cộng, ta có 10 + 5+ 3+ 2= 20 cách chọn.

Chọn đáp án A

Để chọn một chiếc đồng hồ, ta có:

Có 3 cách chọn mặt.

Có 4 cách chọn dây.

Vậy theo qui tắc nhân ta có:3.4 = 12 cách.

Chọn đáp án C

Để chọn một bộ quần-áo-cà vạt , ta có:

Có 4 cách chọn quần.

Có 6 cách chọn áo.

Có 3 cách chọn cà vạt.

Vậy theo qui tắc nhân ta có : 4.6.3 = 72 cách.

Chọn đáp án B

a) Theo quy tắc cộng có: 23 +17 = 40 cách chọn một học sinh tham gia cuộc thi môi trường. Vì vậy chọn đáp án C

b) Việc chọn hai học sinh (nam và nữ) phải tiến hành hai hành động liên tiếp

Hành động 1: chọn 1 học sinh nữ trong số 23 học sinh nữ nên có 23 cách chọn

Hành động 2: chọn 1 học sinh nam nên có 17 cách chọn

Theo quy tắc nhân, có 23.17 = 391 cách chọn hai học sinh tham gia hội trại có cả nam và nữ.

Vì vậy chọn phương án B

a) Việc chọn 3 viên bi khác màu phải tiến hành 3 hành động liên tiếp: chọn 1 bi đỏ trong 7 bi đỏ nên có 7 cách chọn, tương tự có 8 cách chọn 1 bi xanh và 5 cách chọn 1 bi vàng. Theo quy tắc nhân ta có: 7.8.5 = 280 cách. Vậy đáp án là B

b) Muốn lấy được 2 viên bi khác màu từ trong túi đã cho xảy ra các trường hợp sau:

- Lấy 1 bi đỏ và 1 bi xanh: có 7 cách để lấy 1 bi đỏ và 8 cách để lấy 1 bi xanh. Do đó có 7.8 = 56 cách lấy

- Lấy 1 bi đỏ và 1 bi vàng: có 7 cách lấy 1 bi đỏ và 5 cách lấy 1 bi vàng. Do đó co 7.5 = 35 cách lấy

- Lấy 1 bi xanh và 1 bi vàng: có 8 cách để lấy 1 bi xanh và 5 cách để lấy 1 bi vàng. Do đó có 8.5 = 40 cách để lấy

- Áp dụng quy tắc cộng cho 3 trường hợp, ta có 56 + 35 + 40 = 131 cách

Vì vậy chọn đáp án là C

Gọi tập hợp E = {0,1,2,3,4,5}

a) Số tự nhiên có hai chữ số khác nhau có dạng:

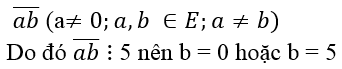
Với b = 0 thì có 5 cách chọn a ( vì a ≠ 0)

Với b = 5 thì có 4 cách chọn a ( vì a ≠ b và a ≠ 0)

Theo quy tắc cộng, có tất cả 5 + 4 = 9 số tự nhiên cần tìm. Chọn đáp án là C.

b) Số tự nhiên có ba chữ số khác nhau có dạng

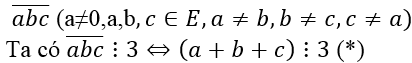
Trong E có các bộ chữ số thoả mãn (*) là:

(0,1,2);(0,1,5);(0,2,4);(1,2,3);(1,3,5);(2,3,4);(3,4,5)

Mỗi bộ gồm ba chữ số khác nhau và khác 0 nên ta viết được 3.2.1 = 6 số có ba chữ số chia hết cho 3

Mỗi bộ gồm ba chữ số khác nhau và có một chữ số 0 nên ta viết được 2.2.1 = 4 số có ba chữ số chia hết cho 3

Vậy theo quy tắc cộng ta có: 6.4 + 4.3 = 36 số có 3 chữ số chia hết cho 3

Chọn đáp án là A

c) Số tự nhiên có 3 chữ số có dạng

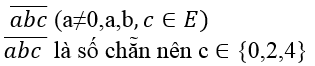
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).

Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)

Ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)

Áp dụng quy tắc nhân ta có 3.6.5 = 90 số có 3 chữ số. Vì vậy đáp án là B

Nếu chọn áo size S thì sẽ có 5 cách.

Nếu chọn áo size M thì sẽ có 4 cách.

Theo qui tắc cộng, ta có 5+ 4= 9 cách chọn mua áo.

Chọn đáp án A

Nếu chọn một cái quần thì sẽ có 4 cách.

Nếu chọn một cái áo thì sẽ có 6 cách.

Nếu chọn một cái cà vạt thì sẽ có 3 cách.

Theo qui tắc cộng, ta có 4 + 6 + 3 = 13 cách chọn.

II. Bài tập tự luận có giải

Bài 1: Số 253125000 có bao nhiêu ước số tự nhiên?

Lời giải:

Ta có 253125000 = 23.34.58 nên mỗi ước số tự nhiên của số đã cho đều có dạng 2m*3n*5p trong đó m, n, p ≠ N sao cho 0 ≤ m ≤ 3; 0 ≤ n ≤ 4; 0 ≤ p ≤ 8.

Có 4 cách chọn m; m ∈{0; 1; 2; 3}

Có 5 cách chọn n; n ∈{0; 1; 2; 3; 4}

Có 9 cách chọn p; p ∈{0; 1; 2; 3; 4; ....; 8}

Vậy theo qui tắc nhân ta có: 4.5.9 = 180 ước số tự nhiên.

Bài 2: Từ các chữ số 1; 5; 6; 7 có thể lập được bao nhiêu chữ số tự nhiên có 4 chữ số (không nhất thiết phải khác nhau) ?

Lời giải:

Gọi số cần tìm có dạng abcd với (a, b, c, d) ∈ A = {1, 5, 6, 7}.

Vì số cần tìm có 4 chữ số không nhất thiết khác nhau nên:

a được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.

b được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.

c được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.

d được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.

Như vậy, ta có 4.4.4.4 = 256 số cần tìm.

Bài 3: Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu chữ số tự nhiên bé hơn 100 ?

Lời giải:

Các số bé hơn 100 chính là các số có một chữ số và hai chữ số được hình thành từ tập A = {1, 2, 3, 4, 5, 6}.

Từ tập A có thể lập được 6 số có một chữ số.

Gọi số có hai chữ số có dạng ab với (a, b) ∈ A.

Trong đó:

a được chọn từ tập A (có 6 phần tử) nên có 6 cách chọn.

b được chọn từ tập A (có 6 phần tử) nên có 6 cách chọn.

Như vậy, ta có 6.6 = 36 số có hai chữ số.

Vậy, từ A có thể lập được 6 + 36 = 42 số tự nhiên bé hơn 100.

Bài 4: Từ các chữ số 0; 1; 2; 3 ;4; 5 có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau ?

Lời giải:

Gọi số cần tìm có dạng abcd với (a, b, c, d) ∈ A = {0, 1, 2, 3, 4, 5}.

Vì abcd là số lẻ ⇒ d = {1, 3, 5} ⇒ d có 3 cách chọn.

Khi đó, a có 4 cách chọn (khác 0 và d),.

b có 4 cách chọn và c có 3 cách chọn.

Vậy có tất cả 3.4.4.3 = 144 số cần tìm.

Bài 5: Từ các chữ số 0; 1; 2; 3; 4; 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau ?

Lời giải:

Gọi số cần tìm có dạng abcd với (a, b, c, d) ∈ A= {0, 1, 2, 3, 4, 5}.

Vì abcd là số chẵn ⇒ d = {0, 2, 4}.

TH1. Nếu d = 0, số cần tìm là abc0 Khi đó:

a được chọn từ tập A\{0} nên có 5 cách chọn.

b được chọn từ tập A\{0, a} nên có 4 cách chọn.

c được chọn từ tập A\{0, a, b} nên có 3 cách chọn.

Như vậy, ta có 5.4.3 = 60 số có dạng abc0

TH2. Nếu d ∈ {2, 4} ⇒ d có 2 cách chọn.

Khi đó, a có 4 cách chọn (khác 0 và d),

b có 4 cách chọn và c có 3 cách chọn.

Như vậy, ta có 2.4.4.3 = 96 số cần tìm như trên.

Vậy có tất cả 60 +96 = 156 số cần tìm.

Bài 6: Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.

Lời giải:

Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:

Có 5 cách chọn hoa hồng trắng.

Có 6 cách chọn hoa hồng đỏ.

Có 7 cách chọn hoa hồng vàng.

Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.

Bài 7: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm một món ăn trong năm món, một loại quả tráng miệng trong năm loại quả tráng miệng và một nước uống trong ba loại nước uống. Có bao nhiêu cách chọn thực đơn.

Lời giải:

Để chọn thực đơn, ta có:

Có 5 cách chọn món ăn.

Có 5 cách chọn quả tráng miệng.

Có 3 cách chọn nước uống.

Vậy theo qui tắc nhân ta có 5.5.3 = 75 cách.

Bài 8: Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng?

Lời giải:

Để chọn một người đàn ông và một người phụ nữ không là vợ chồng, ta có

Có 10 cách chọn người đàn ông.

Có 9 cách chọn người phụ nữ ( trừ 1 người là vợ của người đàn ông đã chọn trước đó).

Vậy theo qui tắc nhân ta có 10.9 = 90 cách

Bài 9: Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

Lời giải:

Từ A đến B có 4 cách.

Từ B đến C có 2 cách.

Từ C đến D có 2 cách.

Vậy theo qui tắc nhân ta có 4.2.3 = 24 cách.

Bài 10: Trong một tuần bạn A dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình (thăm một bạn không quá một lần)?

Lời giải:

Một tuần có bảy ngày và mỗi ngày thăm một bạn.

Có 12 cách chọn bạn vào ngày thứ nhất.

Có 11 cách chọn bạn vào ngày thứ hai ( khác bạn ngày thứ nhất).

Có 10 cách chọn bạn vào ngày thứ ba ( khác bạn ngày thứ nhất, thứ 2)

Có 9 cách chọn bạn vào ngày thứ tư.

Có 8 cách chọn bạn vào ngày thứ năm.

Có 7 cách chọn bạn vào ngày thứ sáu.

Có 6 cách chọn bạn vào ngày thứ bảy.

Vậy theo qui tắc nhân ta có 12.11.10.9.8.7.6 = 3 991 680 cách.

III. Bài tập vận dụng

Bài 1 Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:

a) Một chữ số ?       

b) Hai chứ số ?    

c) Hai chữ số khác nhau ?

Bài 2 Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100 ?

Bài 3 Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da,, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây ?

Bài 4 Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:

a) Một chữ số?

b) Hai chứ số?

c) Hai chữ số khác nhau?

Bài 5 Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100? Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?

Bài 6 Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?

Bài 7 Giả sử bạn muốn mua một áo sơ mi cỡ 39 hoặc cỡ 40. Áo cỡ 39 có 5 màu khác nhau, áo cỡ 40 có 4 màu khác nhau. Hỏi có bao nhiêu sự lựa chon ( về màu sắc và kích cỡ)?

Bài 8 Một người có 4 cái quần khác nhau, 6 cái áo khác nhau, 3 chiếc cà vạt khác nhau. Để chọn một cái quần hoặc một cái áo hoặc 1 cái cà vạt thì số cách chọn khác nhau là?

Bài 9 Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhua và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là?

Bài 10 Trong lớp học có 20 học sinh nam và 24 học sinh nữ. Giáo viên chủ nhiệm cần chọn 2 học sinh: 1 nam và 1 nữ tham gia đội cờ đỏ. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn?

Bài tập Phép quay - Toán 11

I. Bài tập trắc nghiệm

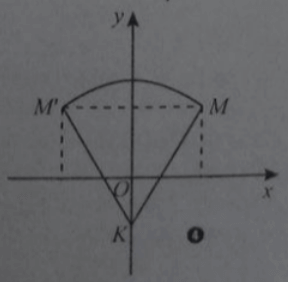
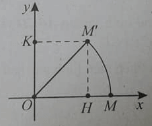
Bài 1: Trong mặt phẳng Oxy phép quay tâm K, góc 60⁰ biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:

A. (0;0)      

B. (0;-$\sqrt{3}$)      

C. (0;1-$\sqrt{3}$)      

D. ($\sqrt{2}$;0)

Lời giải:

Đáp án: C

Tam giác đều KMM’ có cạnh MM’ = 2 nên đường cao bằng $\sqrt{3}$.

Suy ra OK = $\sqrt{3}$-1 ⇒ K(0; 1-$\sqrt{3}$)

Nhận xét. Phép quay có góc quay bằng ±60⁰ thì tam giác tạo bởi tâm quay, điểm M và ảnh M’ của nó luôn tạo thành một tam giác đều.

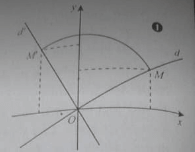
Bài 2: Trong mặt phẳng Oxy phép quay Q(O; 60⁰) biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình:

A. x + 2y = 0

B. 2x + y = 0

C. 2x - y = 0

D. x - y + 2 = 0

Lời giải:

Đáp án: B

Lấy M(2; 1) thuộc d, phép quay Q(O, 90⁰) biến M(2; 1) thành M’(-1; 2). Tâm quay O(0; 0) thuộc d ⇒ d' đi qua O và M’ có phương trình 2x + y = 0.

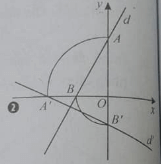
Bài 3: trong mặt phẳng Oxy phép quay Q(O; 90⁰) biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.

A. x + 2y - 1 = 0

B. 2x + y + 1 = 0

C. 2x - y + 1 = 0

D. x + 2y + 1 = 0

Lời giải:

Đáp án: D

Lấy A(0; 1) và B(-$\frac{1}{2}$;0) thuộc d, phép quay Q(O, 90⁰) biến A thành A’(-1; 0), biến B thành B’(0; -$\frac{1}{2}$) phương trình d’ qua A’, B’ là x + 2y + 1 = 0.

Bài 4: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 3)² + y² = 4. Phép quay tâm O(0;0) góc quay 90⁰ biến (C) thành (C’) có phương trình:

A. x² + y² - 6x + 5 = 0

B. x² + y² - 6y + 6 = 0

C. x² + y² + 6x - 6 = 0

D. x² + y² - 6y + 5 = 0

Lời giải:

Đáp án: D

Phép quay tâm O(0; 0) góc quay 90⁰ biến tâm I(3; 0) của (C) thành tâm I’(0; 3) của (C’), bán kính không thay đổi. phương trình (C’) là x² + (y - 3)² = 4 ⇒ x² + y² - 6y + 5 = 0

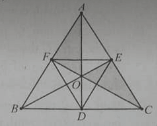
Bài 5: Cho một tam giác ABC tâm O. gọi A, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?

A. Q(0; 120⁰)(∆ODC) = ∆OFA      

B. Q(0; 120⁰)(∆AOF) = ∆BOD

C. Q(0; 120⁰)(∆AOB) = ∆AOC      

D. Q(0; 60⁰)(∆OFE) = ∆ODE

Lời giải:

Đáp án: B

D. Không có trên hình vẽ

Chọn đáp án B

Bài 6: Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là:

A. 90⁰      

B. 60⁰

C. 45⁰      

D. 30⁰

Lời giải:

Đáp án: B

Xét phép quay tâm A góc quay 60⁰ biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng DC thành đường thẳng BE suy ra góc giữa DC và BE bằng góc quay 60⁰. Chọn đáp án B.

Bài 7: Trong mặt phẳng tọa độ Oxy cho điểm M(1;0). Phép quay tâm O góc quay 45⁰ biến M thành M’ có tọa độ

Lời giải:

Đáp án: D

Ta có OM’ = OM = 1; tứ giác OHM’K là hình vuông đường chéo bằng 1 suy ra cạnh bằng $\frac{\sqrt{2}}{2}$. Chọn đáp án D

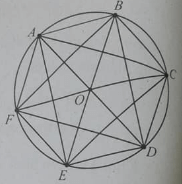
Bài 8: Cho hình lục giác ABCDEF, tâm O. mệnh đề nào sau đây sai?

A. phép quay tâm O góc quay 60⁰ biến tam giác BCD thành tam giác ABC.

B. phép quay tâm O góc quay 120⁰ biến tam giác OEC thành tam giác OCA

C. phép quay tâm O góc quay -60⁰, biến tam giác AFD thành tam giác FEC.

D. phép quay tâm O góc quay -120⁰ biến tam giác BCD thành tam giác DEF.

Lời giải:

Đáp án: C

Phép quay tâm O góc quay -60⁰ biến tam giác AFD thành tam giác ABE.

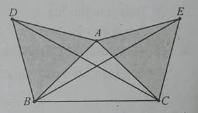
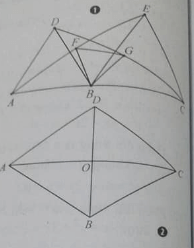
Bài 9: Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là:

A. tam giác thường      

B. tam giác vuông đỉnh B

C. tam giác cân đỉnh B      

D. tam giác đều

Lời giải:

Đáp án: D

(Hình 1) Xét phép quay tâm B góc quay -60⁰ biến A thành D, biến E thành C suy ra phép quay này biến đoạn thẳng AE thành đoạn thẳng DC, suy ra nó biến trung điểm F của AE thành trung điểm G của DC, suy ra nó biến đoạn thẳng BF thành đoạn thẳng BG do đó BF = BG và góc FBG bằng 600. Vậy tam giác BFG là tam giác đều.

Bài 10: Cho hình thoi ABCD có góc A bằng 60⁰.

 a) Phép biến hình nào sau đây biến AB thành BC?

A. Đ0      

B. $\overrightarrow{T2OC}$

C. Q(D; 60⁰)      

D. Q(B; 120⁰)

b) Phép biến hình nào sau đây không biến A thành C?

A. ĐBD      

B. $\overrightarrow{T2OC}$

C. Q(B; 120⁰)      

D. Q(B; 120⁰)

Lời giải:

Đáp án: a - C, b - D

(hình 2)

Chọn đáp án C

Phương án A. Đ0(AB) = CD

Phương án B. T2OC→(AB) = CB' với ACB'B là hình bình hành

Phương án D. Q(B,120⁰)(AB) = A' Bvới A' là điểm đối xứng của D và B.

Góc quay là -120⁰ (thuận chiều kim đồng hồ) thì A biến thành C

II. Bài tập tự luận có lời giải

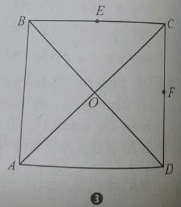
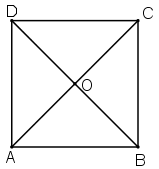
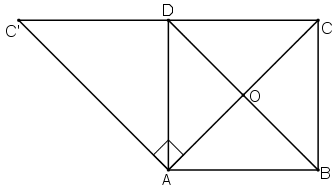
Bài 1: Cho hình vuông ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và CD?

a) phép biến hình nào biến $\overrightarrow{BE}$ thành $\overrightarrow{CF}$

b) phép biến hình nào biến $\overrightarrow{BE}$ thành $\overrightarrow{DF}$?

Lời giải:

a) Xét từng điểm: Phép quay tâm O góc quay -90⁰ biến B thành C, E thành F.

Q(A, 45⁰)(B) = B' ≠ C và Q(A, 45⁰)(E) = E' ≠ F(sai cả hai ảnh)

Q(A, -90⁰)(B) = D và Q(A, 90⁰)(E) = E' ≠ F(sai về chiều góc và ảnh của E)

Q(O, 90⁰)(B) = A và Q(O, -90⁰)(E) = F

b) Nhận xét. Khi luyện tập ta kiểm tra cả bốn phương án và trong mỗi phương án kiểm tra cả hai điểm B, D. còn trong khi kiểm tra, thi cử khi thấy ảnh của một điểm sai thì loại phương án đó; thấy ảnh của cả hai điểm đều đúng thì chọn phương án đó mà không cần kiểm tra các phương án còn lại.

Bài 2: Trong mặt phẳng Oxy, ảnh của điểm M (-6;1) qua phép quay Q(O; 90⁰) là?

Lời giải:

Nhận xét. Cách làm các bài từ 5 đến 9: Vẽ hệ tọa độ Oxy, lấy điểm M, thực hiện phép quay. Chú ý chiều dương là ngược kim đồng hồ, chiều âm thuận chiều kim đồng hồ (hình 1)

Bài 3: Trong mặt phẳng Oxy qua phép quay Q(O; 90⁰) thì M'(2; -3) là ảnh của điểm.

Lời giải:

(hình 2) vẽ ảnh của M’ qua phép quay Q(O, 90⁰) là điểm M (- 3; -2)

Bài 4: Trong mặt phẳng Oxy cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay 45⁰.

Lời giải:

Nhận xét. Hình vuông có cạnh bằng 1 thì đường chéo bằng $\sqrt{2}$.

Bài 5:

Cho hình vuông ABCD tâm O.

a. Tìm ảnh của điểm C qua phép quay tâm A góc 90^o.

b. Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90^o

Lời giải:

a. Gọi C’ là điểm đối xứng với điểm C qua điểm D.

 ⇔ C’ là điểm đối xứng với C qua D.

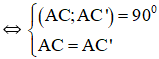
b) Ta có:

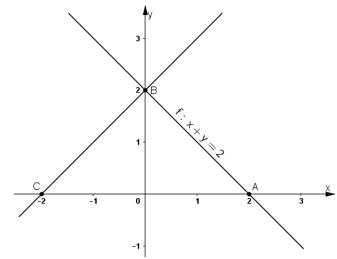
Bài 6 Trong mặt phẳng tọa độ Oxy cho điểm A(2; 0) và đường thẳng d có phương trình x + y – 2 = 0. Tìm ảnh của A và d qua phép quay tâm O góc 90^o.

Lời giải:

* Ta có A(2; 0) thuộc tia Ox.

Gọi Q_(O,90º) (A) = B thì B thuộc tia Oy và OA = OB nên B(0 ; 2).

* Gọi d’ là ảnh của d qua phép quay tâm O, góc quay 90º.

+ A(2 ; 0) ∈ (d)

⇒ B = Q_(O,90º) (A) ∈ (d’)

+ B(0 ; 2) ∈ (d).

⇒ C = Q_(O,90º) (B) ∈ (d’).

Dễ dàng nhận thấy C(-2; 0) (hình vẽ).

⇒ (d’) chính là đường thẳng BC.

Đường thẳng d’ đi qua B(0 ; 2) và C(-2; 0) nên có phương trình đoạn chắn là :

III. Bài tập vận dụng

Bài 1 Cho hình vuông ABCD tâm O

a) Tìm ảnh của điểm C qua phép quay tâm A góc ${90}^0$.

b) Tìm ảnh của đường thẳng BC qua phép quay tâm O góc ${90}^0$.

Bài 2 Trong mặt phẳng tọa độ Oxy cho điểm A(2,0) và đường thẳng d có phương trình . Tìm ảnh của A và d qua phép quay tâm O góc .

Bài 3 Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là?

Bài 4 Cho hình thoi ABCD có góc A bằng ${60}^{\circ }$. Phép biến hình nào biến AB thành BC?

Bài 5 Trong mặt phẳng Oxy phép quay tâm K, góc 60 độ biến M(1;1) thành M’(-1;1). Tọa độ điểm K là?

Bài 6 Trong mặt phẳng Oxy phép quay Q_{(O; 60⁰)} biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình?

Bài 7 trong mặt phẳng Oxy phép quay Q_{(O; 90⁰)} biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.

Bài 8 Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 3)² + y² = 4. Phép quay tâm O(0;0) góc quay 90⁰ biến (C) thành (C’) có phương trình?

Bài 9 Cho một tam giác ABC tâm O. gọi A, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?

Bài 10 Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là?

Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác: