Nội dung bài viết

    Xem thêm

    Bài 5 trang 94 Toán 8 Tập 2 | Cánh diều Giải Toán lớp 8

    Lời giải Bài 5 trang 94 Toán 8 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

    1 327 29/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài tập cuối chương 8 trang 94

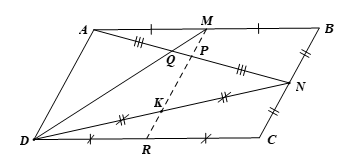
    Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:

    a) MP // AD, MP=14AD;

    b) AQ=25AN;

    c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và PR=34AD.

    Lời giải:

    Bài 5 trang 94 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    a) Do N là trung điểm của BC nên BN=12BC

    Và ABCD là hình bình hành nên BC = AD, BC // AD

    Suy ra BN=12AD,BN // AD (1)

    Xét ∆ABN có M, P lần lượt là trung điểm của AB, AN nên MP là đường trung bình của ∆ABN

    Suy ra MP=12BN và MP // BN (2)

    Từ (1) và (2) ta có MP=12BN=12⋅12AD=14AD và MP // AD.

    Vậy MP // AD và MP=14AD. (3)

    b) Xét ∆ADQ với MP // AD, ta có ADMP=QAQP (hệ quả của định lí Thalès)

    Hay AD14AD=AQPQ nên AQPQ=41

    Suy ra AQPQ+AQ=41+4 hay AQAP=45

    Mà P là trung điểm của AN nên AP=12AN

    Do đó AQ12AN=45, suy ra AQ=45⋅12AN=25AN.

    Vậy AQ=25AN.

    c) Gọi K là trung điểm của DN.

    Xét ∆AND có P, K lần lượt là trung điểm của AN, DN nên PK là đường trung bình của ∆AND. Do đó PK // AD và PK=12AD (4)

    Tương tự, xét ∆CDN có KR là đường trung bình của ∆CDN nên KR // CN và KR=12CN

    Mà N là trung điểm của BC nên CN=12BC=12AD và BC // AD

    Do đó KR // AD và KR=12CN=12⋅12AD=14AD (5)

    Từ (3), (4) và (5), theo tiên đề Euclid ta có: M, P, K, R thẳng hàng.

    Và PR=PK+KR=12AD+14AD=34AD.

    Vậy ba điểm M, P, R thẳng hàng và PR=34AD.

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác: 

    Bài 1 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, E^=60°, M^=40°. a) Số đo góc D bằng bao nhiêu độ? A. 40°.  B. 50°.  C. 60°.  D. 80°...

    Bài 2 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, DE = 2 cm, DG = 4 cm, MN = 4 cm, NP = 6 cm. a) Độ dài cạnh EG là A. 2 cm.  B. 3 cm.  C. 4 cm.  D. 8 cm...

    Bài 3 trang 94 Toán 8 Tập 2: Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). Chứng minh rằng MNBC+NPAB=1...

    Bài 4 trang 94 Toán 8 Tập 2: Cho tứ giác ABCD. Tia phân giác của góc BAD và BCD cắt nhau tại điểm I (Hình 103). Chứng minh AB.CD = AD.BC...

    Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh...

    Bài 6 trang 95 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆A’B’C’ với tỉ số đồng dạng k. a) Gọi AM, AM’ lần lượt là các đường trung tuyến của ∆ABC và ∆A’B’C’...

    Bài 7 trang 95 Toán 8 Tập 2: Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c...

    Bài 8 trang 95 Toán 8 Tập 2: Cho Hình 105. Chứng minh: a) ∆HAB ᔕ ∆HBC; b) HB = HD = 6 cm...

    Bài 9 trang 95 Toán 8 Tập 2: Cho Hình 106. Chứng minh: a) AH2 = AB.AI = AC.AK; b) AIK^=ACH^....

    Bài 10 trang 96 Toán 8 Tập 2: Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC. Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN...

    Bài 11 trang 96 Toán 8 Tập 2: Cho Hình 107. Chứng minh: a) ∆ABN ᔕ ∆AIP và AI.AN = AP.AB b) AI.AN + BI.BM = AB2...

    Bài 12 trang 96 Toán 8 Tập 2: Hình 108 minh họa mặt cắt đứng của tủ sách nghệ thuật ở nhà bác Ngọc. Sau một thời gian sử dụng, tủ sách đó đã có dấu hiệu bị xuống cấp và cần sửa lại...

    Bài 13 trang 96 Toán 8 Tập 2: Cho Hình 109. Hình nào đồng dạng phối cảnh với: a) Tam giác OAB? b) Tam giác OBC? c) Tam giác OCD? d) Tứ giác ABCD...

    Bài 14 trang 96 Toán 8 Tập 2: Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm gợi nên những cặp hình đồng dạng. Hãy viết 6 cặp lá mầm gợi nên những hình đồng dạng.

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác: 

    Bài 7: Trường hợp đồng dạng thứ hai của tam giác

    Bài 8: Trường hợp đồng dạng thứ ba của tam giác

    Bài 9: Hình đồng dạng

    Bài 10: Hình đồng dạng trong thực tiễn

    Chủ đề 3: Thực hành đo chiều cao

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 327 29/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: