Toán 8 Bài 1 (Cánh diều): Phương trình bậc nhất một ẩn

Giải Toán 8 Bài 1: Phương trình bậc nhất một ẩn

Giải Toán 8 trang 39 Tập 2

Khởi động trang 39 Toán 8 Tập 2: Giả sử mỗi hộp màu tím đặt trên đĩa cân ở Hình 1 đều có khối lượng là x (kg), còn mỗi hộp màu vàng đều có khối lượng là x (kg). Gọi A(x), B(x) lần lượt là các biểu thức biểu thị (theo x) tổng khối lượng của các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải. Do cân thăng bằng nên ta có hệ thức: A(x) = B(x).

Hệ thức A(x) = B(x) gợi nên khái niệm nào trong toán học?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Hệ thức A(x) = B(x) là phương trình ẩn x, trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x.

I. Mở đầu về phương trình một ẩn

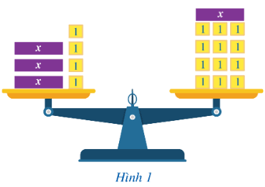
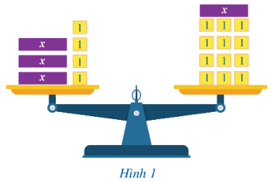
Hoạt động 1 trang 39 Toán 8 Tập 2: Trong bài toán nêu ở phần mở đầu, hãy viết:

a) Các biểu thức A(x), B(x) lần lượt biểu thị (theo x) tổng khối lượng của các hộp xếp

ở đĩa cân bên trái, đĩa cân bên phải;

b) Hệ thức thể hiện sự bằng nhau của hai biểu thức trên.

Lời giải:

a) Biểu thức A(x), B(x) lần lượt biểu thị (theo x) tổng khối lượng của các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải là:

A(x) = x . 3 + 1 . 4 = 3x + 4;

B(x) = x + 1.12 = x + 12.

b) Hệ thức thể hiện sự bằng nhau của hai biểu thức trên là:3x + 4 = x + 12.

Giải Toán 8 trang 40 Tập 2

Hoạt động 2 trang 40 Toán 8 Tập 2: Khi x = 4, tính giá trị mỗi vế của phương trình: 3x + 4 = x + 12 (1). So sánh hai giá trị đó.

Lời giải:

Thay x = 4 vào mỗi vế của phương trình (1) ta được:

VT = 3.4 + 4 = 16.

VP = 4 + 12 = 16.

Do 16 = 16 nên giá trị của hai vế khi x = 4 là bằng nhau.

II. Phương trình bậc nhất một ẩn

Hoạt động 3 trang 40 Toán 8 Tập 2: Quan sát phương trình (ẩn x): 4x + 12 = 0, nếu nhận xét về bậc của đa thức ở vế trái của phương trình đó.

Lời giải:

Bậc của đa thức 4x + 12 là 1.

Luyện tập 1 trang 40 Toán 8 Tập 2: Nêu hai ví dụ về phương trình bậc nhất ẩn x.

Lời giải:

Hai ví dụ về phương trình bậc nhất ẩn x là 3x + 0,5 = 5 và x ‒ 2 = 0.

Luyện tập 2 trang 40 Toán 8 Tập 2: Kiểm tra xem x = ‒3 có là nghiệm của phương trình bậc nhất 5x + 15 = 0 hay không.

Lời giải:

Thay x = ‒ 3 vào vế trái của phương trình ta có:

5 . (‒3) + 15 = ‒15 + 15 = 0.

Vậy x = ‒3 là nghiệm của phương trình 5x + 15 = 0.

Giải Toán 8 trang 41 Tập 2

Hoạt động 4 trang 41 Toán 8 Tập 2: Nêu quy tắc chuyển vế trong một đẳng thức số.

Lời giải:

Khi chuyển một số hạng bất kỳ trong một đẳng thức từ vế bên này sang vế kia thì ta bắt buộc phải đổi dấu số hạng đó:

⦁ Nếu số hạng được chuyển là một số dương thì đổi từ dấu cộng thành dấu trừ;

⦁ Nếu số hạng được chuyển là một số âm thì đổi từ dấu trừ thành dấu cộng.

Hoạt động 5 trang 41 Toán 8 Tập 2: Xét đẳng thức số: 2 + 3 – 4 = 9 – 10 + 2. Tính giá trị mỗi vế của đẳng thức đó khi nhân cả hai vế với 5 và so sánh hai giá trị nhận được.

Lời giải:

Xét đẳng thức số: 2 + 3 – 4 = 9 – 10 + 2, ta có:

⦁ Giá trị của vế trái khi nhân với 5 là: (2 + 3 – 4) . 5 = 1 . 5 = 5;

⦁ Giá trị của vế phải khi nhân với 5 là: (9 – 10 + 2) . 5 = 1 . 5 = 5.

Do 5 = 5 nên giá trị mỗi vế của đẳng thức đã cho khi nhân cả hai vế với 5 là bằng nhau.

Hoạt động 6 trang 41 Toán 8 Tập 2: Áp dụng quy tắc chuyển vế và quy tắc nhân, hãy giải phương trình: 5x – 30 = 0 (2).

Lời giải:

Áp dụng quy tắc chuyển vế và quy tắc nhân, ta giải phương trình (2) như sau:

5x – 30 = 0

5x = 30 ← Chuyển –30 sang vế phải và đổi dấu

x = 30 : 5 ← Chia cả hai vế của phương trình cho 5

x = 6.

Vậy phương trình (2) có nghiệm x = 6.

Giải Toán 8 trang 42 Tập 2

Luyện tập 3 trang 42 Toán 8 Tập 2: Giải các phương trình:

a) ‒6x ‒ 15 = 0; b) $-\frac{9}{2}x+21=0.$

Lời giải:

a) ‒6x ‒ 15 = 0

‒6x = 15

$x=-\frac{15}{6}$

Vậy phương trình có nghiệm $x=-\frac{15}{6}.$

b) $-\frac{9}{2}x+21=0$

$-\frac{9}{2}x=-21$

$x=-21:\left(-\frac{9}{2}\right)$

$x=-21\cdot \left(-\frac{2}{9}\right)$

$x=\frac{14}{3}$

Vậy phương trình có nghiệm $x=\frac{14}{3}.$

Hoạt động 7 trang 42 Toán 8 Tập 2: Giải phương trình: 3x + 4 = x + 12.

Lời giải:

3x + 4 = x + 12

3x + 4 – x = 12 ← Chuyển các số hạng chứa ẩn sang một vế

2x = 12 – 4 ← Chuyển các hằng số sang vế còn lại

2x = 8

x = 4.

Vậy phương trình có nghiệm x = 4.

Luyện tập 4 trang 42 Toán 8 Tập 2: Giải phương trình: 2(x ‒ 0,7) ‒ 1,6 = 1,5 ‒ (x + 1,2)

Lời giải:

2(x ‒ 0,7) ‒ 1,6 = 1,5 ‒ (x + 1,2)

2x ‒ 1,4 ‒ 1,6 = 1,5 ‒ x ‒ 1,2

2x + x = 1,5 ‒ 1,2 + 1,4 + 1,6

3x = 3,3

x = 1,1

Vậy phương trình có nghiệm x = 1,1.

Bài tập

Giải Toán 8 trang 43 Tập 2

Bài 1 trang 43 Toán 8 Tập 2: Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.

a) 3x + 9 = 0 với x = 3; x = ‒3.

b) 2 ‒ 2x = 3x + 1 với $x=-\frac{1}{5};x=\frac{1}{5}.$

Lời giải:

a) • Thay x = 3 vào vế trái của phương trình ta có:

3.3 + 9 = 9 + 9 = 18 ≠ 0.

Vậy x = 3 không là nghiệm của phương trình 3x + 9 = 0.

• Thay x = ‒3 vào vế trái của phương trình ta có:

3.(‒3) + 9 = ‒9 + 9 = 0

Vậy x = ‒3 là nghiệm của phương trình 3x + 9 = 0.

b) • Thay $x=-\frac{1}{5}$ vào 2vế của phương trình ta có:

$VT=2-2\cdot \left(-\frac{1}{5}\right)=2+\frac{2}{5}=\frac{12}{5};$

$VP=3\cdot \left(-\frac{1}{5}\right)+1=-\frac{3}{5}+1=\frac{2}{5}.$

Do đó, giá trị của vế trái khác giá trị của vế phải.

Vậy $x=-\frac{1}{5}$không là nghiệm của phương trình 2 ‒ 2x = 3x + 1.

• Thay $x=\frac{1}{5}$ vào 2 vế của phương trình ta có:

$VT=2-2\cdot \frac{1}{5}=2-\frac{2}{5}=\frac{8}{5};$

$VP=3\cdot \frac{1}{5}+1=\frac{3}{5}+1=\frac{8}{5}.$

Do đó, giá trị của vế trái bằnggiá trị của vế phải.

Vậy $x=\frac{1}{5}$là nghiệm của phương trình 2 ‒ 2x = 3x + 1.

Bài 2 trang 43 Toán 8 Tập 2: Tìm chỗ sai trong mỗi lời giải sau và giải lại cho đúng:

a) 5 ‒ (x + 8) = 3x + 3(x ‒ 9)

5 ‒ x + 8 = 3x + 3x ‒ 27

13 ‒ x = 6x ‒ 27

‒x ‒ 6x = ‒27 + 13

‒7x = ‒14

x = (‒14) : (‒7)

x = 2.

Vậy phương trình có nghiệm x = 2.

b) 3x ‒ 18 + x = 12 ‒ (5x + 3)

4x ‒ 18 = 12 ‒ 5x ‒ 3

4x + 5x = 9 ‒ 18

9x = ‒9

x = (‒9) : 9

x = ‒1.

Vậy phương trình có nghiệm x = ‒1.

Lời giải:

a) Khi bỏ dấu ngoặc (x + 8) trước dấu ngoặc là dấu trừ phải đổi dấu trong ngoặc đó. Vì vậy lời giải trên sai ở bước thứ hai. Ta có thể giải lại như sau:

5 ‒ (x + 8) = 3x + 3(x ‒ 9)

5 ‒ x ‒ 8 = 3x + 3x ‒ 27

‒3 ‒ x = 6x ‒ 27

‒x ‒ 6x = ‒27 + 3

‒7x = ‒24

x = ‒24 : (‒7)

Vậy phương trình có nghiệm $x=\frac{27}{7}.$

b) Khi chuyển số hạng ‒18 từ vế trái sang vế phải, ta phải đổi dấu số hạng đó. Vì vậy, lời giải trên sai từ bước thứ ba. Ta có thể giải lại như sau:

3x ‒ 18 + x = 12 ‒ (5x + 3)

4x ‒ 18 = 12 ‒ 5x ‒ 3

4x + 5x = 9 + 18

9x = 27

x = 27 : 9

x = 3.

Vậy phương trình có nghiệm x = 3.

Giải Toán 8 trang 44 Tập 2

Bài 3 trang 44 Toán 8 Tập 2: Giải các phương trình:

a) 6x + 4 = 0; b) ‒14x ‒ 28 = 0;

c) $\frac{1}{3}x-5=0;$ d) 3y ‒ 1 = ‒y + 19;

e) ‒2(z + 3) ‒ 5 = z + 4; g) 3(t ‒ 10) = 7(t ‒ 10).

Lời giải:

a) 6x + 4 = 0

6x = ‒4

x = ‒4 : 6

$x=-\frac{2}{3}.$

Vậy phương trình có nghiệm $x=-\frac{2}{3}.$

b) ‒14x ‒ 28 = 0

‒14x = 28

x = 28 : (‒14)

x = ‒2.

Vậy phương trình có nghiệm x = ‒2.

c) $\frac{1}{3}x-5=0$

$\frac{1}{3}x=5$

$x=5:\frac{1}{3}$

x = 5 . 3

x = 15.

Vậy phương trình có nghiệm x = 15.

d) 3y ‒ 1 = ‒y + 19

3y + y = 19 + 1

4y = 20

y = 20 : 4

y = 5.

Vậy phương trình có nghiệm y = 5.

e) ‒2(z + 3) ‒ 5 = z + 4

‒2z ‒ 6 ‒ 5 = z + 4

‒2z ‒ z = 4 + 6 + 5

‒3z = 15

z = 15 : (‒3)

z = ‒5.

Vậy phương trình có nghiệm z = ‒5

g) 3(t ‒ 10) = 7(t ‒ 10).

3t ‒ 30 = 7t ‒ 70

3t ‒ 7t = ‒ 70 + 30

‒4t = ‒ 40

t = ‒ 40 : (‒4)

t = 10

Vậy phương trình có nghiệm t = 10.

Bài 4 trang 44 Toán 8 Tập 2: Giải các phương trình:

a) $\frac{5x-2}{3}=\frac{5-3x}{2};$

b) $\frac{10x+3}{12}=1+\frac{6+8x}{9};$

c) $\frac{7x-1}{6}+2x=\frac{16-x}{5}.$

Lời giải:

a) $\frac{5x-2}{3}=\frac{5-3x}{2}$

$\frac{2\cdot \left(5x-2\right)}{6}=\frac{3\cdot \left(5-3x\right)}{6}$

10x ‒ 4 = 15 ‒ 9x

10x + 9x = 15 + 4

19x = 19

x = 19 : 19

x = 1.

Vậy phương trình có nghiệm x = 1.

b) $\frac{10x+3}{12}=1+\frac{6+8x}{9}$

$\frac{3\cdot \left(10x+3\right)}{36}=\frac{36\cdot 1}{36}+\frac{4\cdot \left(6+8x\right)}{36}$

30x + 9 = 36 + 24 + 32x

30x ‒ 32x = 36 + 24 ‒ 9

‒2x = 51

x = 51 : (‒2)

$x=-\frac{51}{2}.$

Vậy phương trình có nghiệm $x=-\frac{51}{2}.$

c) $\frac{7x-1}{6}+2x=\frac{16-x}{5}$

$\frac{5\cdot \left(7x-1\right)}{30}+\frac{2x\cdot 30}{30}=\frac{6\cdot \left(16-x\right)}{30}$

35x ‒ 5 + 60x = 96 ‒ 6x

35x + 60x + 6x = 96 + 5

101x = 101

x = 101 : 101

x = 1.

Vậy phương trình có nghiệm x = 1.

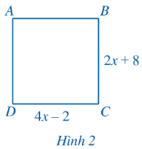
Bài 5 trang 44 Toán 8 Tập 2: Tìm x, biết tứ giác ABCD ở Hình 2 là hình vuông.

Lời giải:

Do ABCD là hình vuông nên CD = BC hay 4x ‒ 2 = 2x + 8

Giải phương trình 4x ‒ 2 = 2x + 8 như sau:

4x ‒ 2 = 2x + 8

4x ‒ 2x = 8 + 2

2x = 10

x = 10 : 2

x = 5.

Vậy x = 5.

Bài 6 trang 44 Toán 8 Tập 2: Hình tam giác và hình chữ nhật ở Hình 3 có cùng chu vi. Viết phương trình biểu thị sự bằng nhau của chu vi hình tam giác, hình chữ nhật đó và tìm x.

Lời giải:

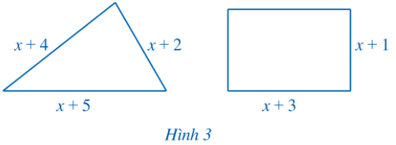
Chu vi hình tam giác là: x + 4 + x + 2 + x + 5 = 3x + 11.

Chu vi hình chữ nhật là: (x + 1 + x + 3) . 2 = (2x + 4) . 2 = 4x + 8

Do chu vi hình tam giác bằng chi vi hình chữ nhật nên ta có phương trình:

3x + 11 = 4x + 8.

Vậy phương trình biểu thị sự bằng nhau của chu vi hình tam giác, hình chữ nhật đó là 3x + 11 = 4x + 8.

Giải phương trình trên như sau:

3x + 11 = 4x + 8.

3x ‒ 4x = 8 ‒ 11

‒x = ‒3

x = 3

Vậy x = 3.

Bài 7 trang 44 Toán 8 Tập 2: Trong phòng thí nghiệm, chị Loan sử dụng cân Roberval để cân: bên đĩa thứ nhất đặt một quả cân nặng 500 g; bên đĩa thứ hai đặt hai vật cùng cân nặng x (g) và ba quả cân nhỏ, mỗi quả cân đó nặng 50 g. Chị Loan thấy cân thăng bằng. Viết phương trình ẩn x biểu thị sự thăng bằng của cân khi đó.

Lời giải:

Số cân nặng đặt bên đĩa thứ nhất là: 500 (g).

Số cân nặng đặt bên đĩa thứ hai là: 2x+3.50 = 2x + 150(g).

Phương trình ẩn x biểu thị sự thăng bằng của cân khi đó là:

500 = 2x + 150.

Bài 8 trang 44 Toán 8 Tập 2: Hình 4 mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1 ft = 0,3048 (m). Tốc độ v (ft/s) của nước tại thời điểm t (s) được cho bởi công thức: v = 48 ‒ 32t. Tìm thời gian để nước đi từ mặt đài phun nước đến khi đạt được độ cao tối đa.

Lời giải:

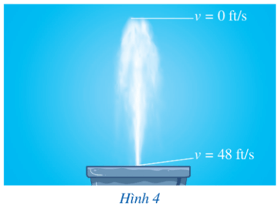
Khi nước đạt đến độ cao tối đa thì v= 0 ft/s.

Suy ra tại thời điểm nước đạt đến độ cao tối đa ta có phương trình: 48−32t=0.

Giải phương trình trên như sau:

48−32t=0

‒32t = ‒ 48

t = ‒48 : (‒32)

t = 1,5

Vậy thời gian để nước đi từ mặt đài phun nước đến khi đạt được độ cao tối đa là 1,5 s.

Lý thuyết Phương trình bậc nhất một ẩn

1. Khái niệm:

Một phương trình với ẩn x có dạng $A\left(x\right)=B\left(x\right)$, trong đó vế trái A(x) và vế phải B(x) là hai biểu thức có cùng một biến x.

Ví dụ: $3x--1=2x+3;3x=5$ là các phương trình ẩn x.

Nếu hai vế của một phương trình (ẩn x) nhận cùng một giá trị khi x = a thì số a gọi là một nghiệm của phương trình đó.

Ví dụ: $x=2$ là nghiệm của phương trình $2x=x+2$ vì thay $x=2$ vào phương trình, ta được 2.2 = 2 + 2

Khi bài toán yêu cầu giải một phương trình, ta phải tìm tất cả các nghiệm của phương trình đó.

Ví dụ: Giải phương trình: $3x+6=0$

Ta có: $3x+6=0\iff 3x=-6\iff x=-2$

Vậy tập nghiệm của phương trình là S = {-2}

2. Phương trình bậc nhất một ẩn và cách giải

Khái niệm: Phương trình dạng ax + b = 0, với a, b là hai số đã cho và $a\ne 0$, được gọi là phương trình bậc nhất một ẩn.

Cách giải:

Đối với phương trình, ta cũng có quy tắc chuyển vế như sau: Trong một phương trình, ta có thể chuyển một số hạng tử vế này sang vế kia và đổi dấu số hạng đó.

Đối với phương trình, ta cũng có quy tắc nhân với một số ( gọi tắt là quy tắc nhân) như sau: Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.

Tương tự, Trong một phương trình, ta có thể chia cả hai vế cho cùng một số khác 0.

Phương trình bậc nhất ax + b = 0 ($a\ne 0$) được giải như sau:

$\begin{array}{c}ax+b=0\\ ax=-b\\ x=-\frac{b}{a}\end{array}$

Phương trình bậc nhất ax + b = 0 ($a\ne 0$) luôn có một nghiệm duy nhất là $x=-\frac{b}{a}$.

Ví dụ: Giải phương trình: $3x+11=0$

Ta có: $3x+11=0\iff 3x=-11\iff x=-\frac{11}{3}$

Vậy nghiệm của phương trình là $x=-\frac{11}{3}$.

Nhận xét: Bằng cách tương tự như trên, ta có thể giải được phương trình dạng:

$ax+b=cx+d(a\ne c)$

Ví dụ: Giải phương trình: $7x--\left(2x+3\right)=5\left(x--2\right)$

$\begin{array}{c}11x--\left(2x+3\right)=6\left(x--2\right)\\ 11x-2x-3=6x-12\\ 11x-2x-6x=-12+3\\ 3x=-9\\ x=\frac{-9}{3}\\ x=-3\end{array}$

Vậy nghiệm của phương trình là x = -3

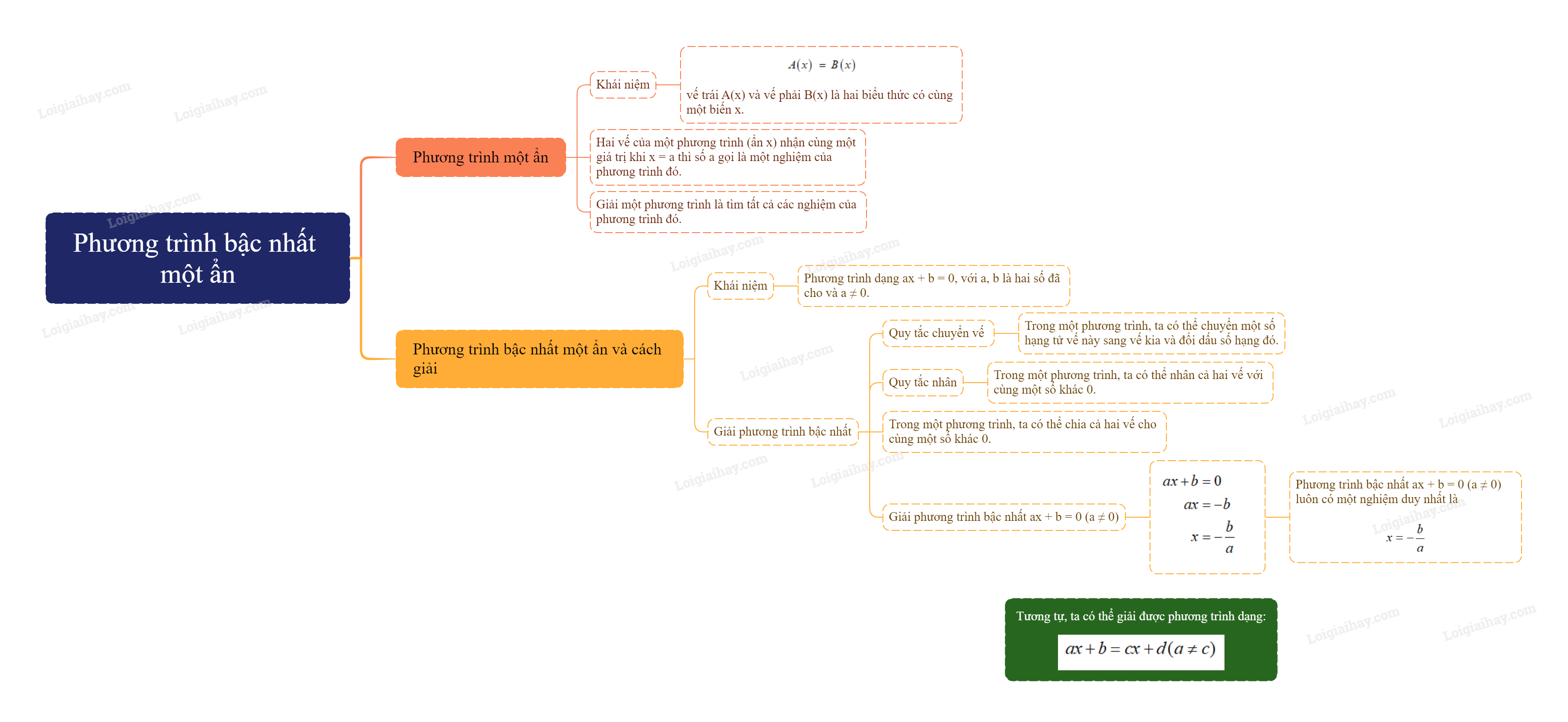
Sơ đồ tư duy Phương trình bậc nhất một ẩn

Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 4: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Bài 5: Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Bài tập cuối chương 6 trang 37

Bài 2: Ứng dụng của phương trình bậc nhất một ẩn

Bài tập cuối chương 7 trang 50