Toán 8 Bài 5 (Cánh diều): Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Giải Toán 8 Bài 5: Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Giải Toán 8 trang 31 Tập 2

Khởi động trang 31 Toán 8 Tập 2: Sau khi tung một đồng xu 15 lần liên tiếp, bạn Thảo kiểm đếm được mặt N xuất hiện 8 lần.

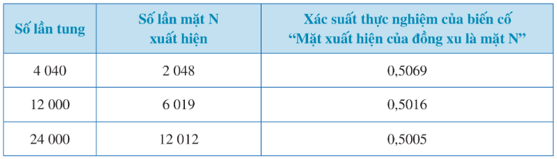
⦁ Xác suất thực nghiệm của biến cố ngẫu nhiên “Mặt xuất hiện của đồng xu là mặt N” là bao nhiêu?

⦁ Xác suất thực nghiệm đó có mối liên hệ gì với xác suất của biến cố ngẫu nhiên trên?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

⦁ Do sau khi tung đồng xu 15 lần liên tiếp được 8 lần xuất hiện mặt N nên xác suất thực nghiệm của biến cố ngẫu nhiên “Mặt xuất hiện của đồng xu là mặt N” là: $\frac{8}{15}.$

⦁ Khi số lần tung đồng xu càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” ngày càng gần với xác suất của biến cố ngẫu nhiên đó (xác suất của biến cố ngẫu nhiên bằng 0,5).

I. Xác suất thực nghiệm của một biến cố trong trò chơi tung đồng xu

Hoạt động 1 trang 31 Toán 8 Tập 2: Sau khi tung một đồng xu 20 lần liên tiếp, bạn Thảo kiểm đếm được mặt N xuất hiện 11 lần. Viết tỉ số của số lần xuất hiện mặt N và tổng số lần tung đồng xu.

Lời giải:

Tỉ số của số lần xuất hiện mặt N và tổng số lần tung đồng xu là: $\frac{11}{20}.$

Giải Toán 8 trang 32 Tập 2

Luyện tập 1 trang 32 Toán 8 Tập 2: Nếu tung một đồng xu 40 lần liên tiếp, có 19 lần xuất hiện mặt N thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng bao nhiêu?

Lời giải:

Khi tung đồng xu 40 lần liên tiếp, có 19 lần xuất hiện mặt N nên số lần mặt S xuất hiện là 40 – 19 = 21 lần.

Vì vậy, xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” là $\frac{21}{40}.$

Hoạt động 2 trang 32 Toán 8 Tập 2: Đọc kĩ các nội dung sau.

Bá tước George–Louis Leclerc de Buffon (1707 – 1788, người Pháp) là một nhà khoa học nghiên cứu về Thực vật, Động vật, Trái Đất, Lịch sử tự nhiên, ... Ông đã thí nghiệm việc tung đồng xu nhiều lần và thu được kết quả sau:

Sau này, người ta chứng minh được rằng số lần tung ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” ngày càng gần với 0,5. Như chúng ta đã biết số 0,5 là xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt N”.

Lời giải:

Học sinh đọc kĩ nội dung trên theo hướng dẫn của Giáo viên.

II. Xác suất thực nghiệm của một biến cố trong trò chơi gieo xúc xắc

Giải Toán 8 trang 33 Tập 2

Hoạt động 3 trang 33 Toán 8 Tập 2: Sau khi gieo ngẫu nhiên xúc xắc 20 lần liên tiếp, bạn Vinh kiểm đếm được mặt 1 chấm xuất hiện 3 lần. Viết tỉ số của số lần xuất hiện mặt 1 chấm và tổng số lần gieo xúc xắc.

Lời giải:

Tỉ số của số lần xuất hiện mặt 1 chấm và tổng số lần gieo xúc xắc là $\frac{3}{20}.$

Luyện tập 2 trang 33 Toán 8 Tập 2: Gieo xúc xắc 30 lần liên tiếp, có 4 lần xuất hiện mặt 2 chấm. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 2 chấm”.

Lời giải:

Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 2 chấm” là $\frac{4}{30}=\frac{2}{15}.$

II. Xác suất thực nghiệm của một biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

Giải Toán 8 trang 34 Tập 2

Hoạt động 4 trang 34 Toán 8 Tập 2: Một hộp có 1 quả bóng màu xanh, 1 quả bóng màu đỏ và 1 quả bóng màu vàng; các quả bóng có kích thước và khối lượng như nhau. Mỗi lần bạn Châu lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Sau 20 lần lấy bóng liên tiếp, bạn Châu kiểm đếm được quả bóng màu xanh xuất hiện 7 lần. Viết tỉ số của số lần xuất hiện quả bóng màu xanh và tổng số lần lấy bóng.

Lời giải:

Tỉ số của số lần xuất hiện quả bóng màu xanh và tổng số lần lấy bóng là: $\frac{7}{20}.$

Giải Toán 8 trang 35 Tập 2

Luyện tập 3 trang 35 Toán 8 Tập 2: Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 10, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp. Sau 40 lần lấy thẻ liên tiếp, thẻ ghi số 1 được lấy ra 3 lần. Tính xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 1” trong trò chơi trên.

Lời giải:

Xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 1” trong trò chơi trên là: $\frac{3}{40}.$

Bài tập

Giải Toán 8 trang 36 Tập 2

Bài 1 trang 36 Toán 8 Tập 2: Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” trong mỗi trường hợp sau:

a) Tung một đồng xu 50 lần liên tiếp, có 27 lần xuất hiện mặt S;

b) Tung một đồng xu 45 lần liên tiếp, có 24 lần xuất hiện mặt N.

Lời giải:

a) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” là: $\frac{27}{50}.$

b) Khi tung đồng xu 45 lần liên tiếp, do mặt N xuất hiện 24 lần nên số lần mặt S xuất hiện là 45 – 24 = 21 lần.

Do đó, xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” là: $\frac{21}{50}.$

Bài 2 trang 36 Toán 8 Tập 2: Gieo một xúc xắc 30 lần liên tiếp, ghi lại mặt xuất hiện của xúc xắc sau mỗi lần gieo. Tính xác suất thực nghiệm của mỗi biến cố sau:

a) “Mặt xuất hiện của xúc xắc là mặt 3 chấm”.

b) “Mặt xuất hiện của xúc xắc là mặt 4 chấm”.

Lời giải:

Ghi lại số chấm xuất hiện ở mỗi lần gieo ta được kết quả như sau:

Chú ý: Kết quả được ghi lại ở trên là ngẫu nhiên.

a) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 3 chấm” là: $\frac{6}{30}=\frac{1}{5}.$

b) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 4 chấm” là: $\frac{4}{30}=\frac{2}{15}.$

Bài 3 trang 36 Toán 8 Tập 2: Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” ngày càng gần với số thực nào?

Lời giải:

Tập hợp các kết quả có thể xảy ra đối với số chấm trên mặt xuất hiện khi gieo xúc xắc là A = {1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm}.

Các kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” là 2, 4, 6. Do đó, có 3 kết quả thuận lợi cho biến cố đó.

Vì vậy, xác suất của biến cố đó là $\frac{3}{6}=\frac{1}{2}.$

Vậy khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” ngày càng gần với $\frac{1}{2}.$

Bài 4 trang 36 Toán 8 Tập 2: Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 10, hai thẻ khác nhau thì ghi hai số khác nhau.

Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp.

a) Sau 30 lần rút thẻ liên tiếp, tính xác suất thực nghiệm của mỗi biến cố sau:

–“Thẻ rút ra ghi số 1”;

–“Thẻ rút ra ghi số 5”;

–“Thẻ rút ra ghi số 10”.

b) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số chia hết cho 3” với xác suất của biến cố đó khi số lần rút thẻ ngày càng lớn.

Lời giải:

Tập hợp các kết quả có thể xảy ra đối với số được ghi trên thẻ khi lấy ngẫu nhiên một chiếc thẻ trong hộp là A = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.

Tập hợp A có 10 phần tử.

a) Ghi lại số của thẻ lấy ra sau 30 lần rút thẻ liên tiếp, ta được kết quả như sau:

Chú ý: Kết quả được ghi lại ở trên là ngẫu nhiên.

⦁ Xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số 1” là $\frac{5}{30}=\frac{1}{6}.$

⦁ Xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số 5” là $\frac{1}{30}.$

⦁ Xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số 10” là $\frac{2}{30}=\frac{1}{15}.$

b) Các kết quả thuận lợi cho biến cố “Thẻ rút ra ghi số chia hết cho 3” là 3; 6; 9. Do đó, có 3 kết quả thuận lợi với biến cố đó.

Vì vậy, xác suất của biến cố “Thẻ rút ra ghi số chia hết cho 3” là $\frac{3}{10}$

Vậy, khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số chia hết cho 3” ngày càng gần với $\frac{3}{10}.$

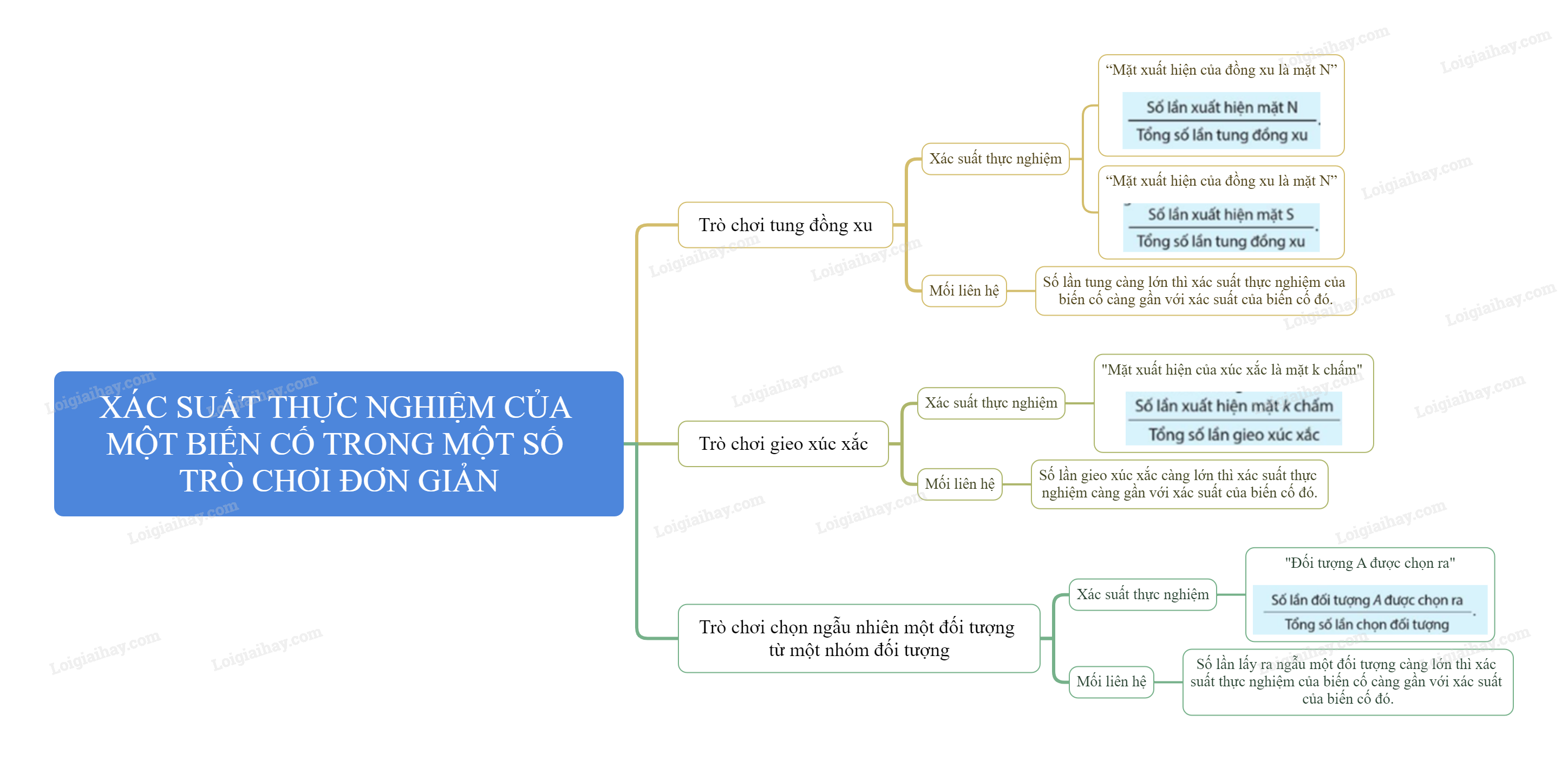
Lý thuyết Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

1. Xác suất thực nghiệm của một biến cố trong trò chơi tung đồng xu

Khái niệm:

- Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” khi tung đồng xu nhiều lần bằng

- Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” khi tung đồng xu nhiều lần bằng

• Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Trong trò chơi tung đồng xu, khi số lần tung ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” (hoặc biến cố “Mặt xuất hiện của đồng xu là mặt S”) ngày càng gần với xác suất của biến cố đó.

2. Xác suất thực nghiệm của một biến cố trong trò chơi gieo xúc xắc

• Khái niệm: Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt k chấm” ($k\in \mathbb{N},1\le k\le 6$) khi gieo xúc xắc nhiều lần bằng

• Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của một biến cố ngày càng gần với xác suất của biến cố đó.

3. Xác suất thực nghiệm của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

• Khái niệm:

Xác suất thực nghiệm của biến cố “Đối tượng A được chọn ra” khi chọn đối tượng nhiều lần bằng

• Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Khi số lần lấy ra ngẫu một đối tượng ngày càng lớn thì xác suất thực nghiệm của biến cố “Đối tượng lấy ra là đối tượng A” ngày càng gần với xác suất của biến cố đó.

Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 4: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Bài tập cuối chương 6 trang 37

Bài 1: Phương trình bậc nhất một ẩn

Bài 2: Ứng dụng của phương trình bậc nhất một ẩn

Bài tập cuối chương 7 trang 50