Toán 8 Bài 4 (Cánh diều): Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Giải Toán 8 Bài 4: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Giải Toán 8 trang 26 Tập 2

Khởi động trang 26 Toán 8 Tập 2: Quan sát đồng xu ở Hình 37. Ta quy ước: mặt xuất hiện số 5 000 là mặt sấp hay mặt S; mặt xuất hiện Quốc huy Việt Nam là mặt ngửa hay mặt N.

Tung đồng xu 1 lần. Xét biến cố ngẫu nhiên “Mặt xuất hiện của đồng xu là mặt N”.

Làm thế nào để tính được xác suất của biến cố ngẫu nhiên nói trên?

Lời giải:

Sau bài học này, chúng ta có thể giải quyết được câu hỏi trên như sau:

Ta có tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là A = {S, N}. Tập hợp này có 2 phần tử.

Có một kết quả thuận lợi cho biến cố “Mặt xuất hiện của đồng xu là mặt N” là mặt N.

Vậy xác suất của biến cố đó là $\frac{1}{2}$.

I. Xác suất của biến cố trong trò chơi tung đồng xu

Hoạt động 1 trang 26 Toán 8 Tập 2: Tung đồng xu 1 lần.

a) Viết tập hợp A gồm các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu.

b) Viết tập hợp gồm các kết quả có thể xảy ra đối với biến cố B: “Mặt xuất hiện của đồng xu là mặt N”. Mỗi phần tử của tập hợp đó gọi là một kết quả thuận lợi cho biến cố B.

c) Tìm tỉ số của số các kết quả thuận lợi cho biến cố B và số phần tử của tập hợp A.

Lời giải:

a) Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là A = {S; N}.

b) Có 1 kết quả thuận lợi cho biến cố B là mặt N nên tập hợp gồm các kết quả có thể xảy ra đối với biến cố B là: {N}.

c) Tỉ số của số các kết quả thuận lợi cho biến cố B và số phần tử của tập hợp A là $\frac{1}{2}$

II. Xác suất của biến cố trong trò chơi vòng quay số

Giải Toán 8 trang 27 Tập 2

Hoạt động 2 trang 27 Toán 8 Tập 2: Hình 38 mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8, chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

Quay đĩa tròn một lần.

a) Viết tập hợp C gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.

b) Viết tập hợp gồm các kết quả có thể xảy ra đối với biến cố D: “Chiếc kim chỉ vào hình quạt ghi số lẻ”. Mỗi phần tử của tập hợp đó gọi là một kết quả thuận lợi cho biến cố D.

c) Tìm tỉ số của số các kết quả thuận lợi cho biến cố D và số phần tử của tập hợp C.

Lời giải:

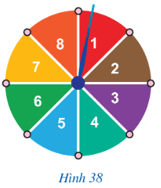
a) Tập hợp gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại là C = {1; 2; 3; 4; 5; 6; 7; 8}.

b) Tập hợp gồm các kết quả có thể xảy ra đối với biến cố D là {1; 3; 5; 7}.

c) Tỉ số của số các kết quả thuận lợi cho biến cố D và số phần tử của tập hợp C là: $\frac{4}{8}=\frac{1}{2}.$

Luyện tập 1 trang 27 Toán 8 Tập 2: Trong trò chơi vòng quay số ở Hoạt động 2, tính xác suất của biến cố “Chiếc kim chỉ vào hình quạt ghi số nhỏ hơn 6”.

Lời giải:

Có 5 kết quả thuận lợi cho biến cố “Chiếc kim chỉ vào hình quạt ghi số nhỏ hơn 6”, đó là: 1; 2; 3; 4; 5.

Vì thế, xác suất của biến cố đó là $\frac{5}{8}.$

III. Xác suất của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

Giải Toán 8 trang 28 Tập 2

Hoạt động 3 trang 28 Toán 8 Tập 2: Một hộp có 10 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó tên 4 loài thực vật là: Lúa, Ngô, Hoa hồng, Hoa hướng dương và tên 6 loài động vật là: Trâu, Bò, Voi, Hổ, Báo, Sư tử; hai viên bi khác nhau thì viết hai tên khác nhau.

Lấy ngẫu nhiên một viên bi trong hộp.

a) Viết tập hợp E gồm các kết quả có thể xảy ra đối với tên sinh vật được viết trên viên bi lấy ra.

b) Viết tập hợp gồm các kết quả có thể xảy ra đối với biến cố G: “Trên viên bi lấy ra viết tên một loài động vật”. Mỗi phần tử của tập hợp đó gọi là một kết quả thuận lợi cho biến cố G.

c) Tìm tỉ số của số các kết quả thuận lợi cho biến cố G và số phần tử của tập hợp E.

Lời giải:

a) Tập hợp gồm các kết quả có thể xảy ra đối với tên sinh vật được viết trên viên bi lấy ra là E = {Lúa; Ngô; Hoa hồng; Hoa hướng dương; Trâu; Bò; Voi; Hổ; Báo; Sư tử}.

b) Tập hợp gồm các kết quả có thể xảy ra đối với biến cố G là {Trâu; Bò; Voi; Hổ; Báo; Sư tử}.

c) Tỉ số của số các kết quả thuận lợi cho biến cố G và số phần tử của tập hợp E là: $\frac{6}{10}=\frac{3}{5}.$

Giải Toán 8 trang 29 Tập 2

Luyện tập 2 trang 29 Toán 8 Tập 2: Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của biến cố “Số tự nhiên được viết ra là số chia cho 9 dư 1”.

Lời giải:

Tập hợp gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:

A = {10; 11; 12; ...; 99}.

Tập hợp A có (99 – 10) + 1 = 90 phần tử.

Các kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chia cho 9 dư 1” là: 10; 19; 28; 37; 46; 55; 64; 73; 82; 91. Do đó, có 10 kết quả thuận lợi cho biến cố đó.

Vì thế, xác suất của biến cố đó là $\frac{10}{90}=\frac{1}{9}.$

Bài tập

Giải Toán 8 trang 30 Tập 2

Bài 1 trang 30 Toán 8 Tập 2: Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 52; hai thẻ khác nhau thì ghi hai số khác nhau.

Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:

a) “Số xuất hiện trên thẻ được rút ra là số có chữ số hàng đơn vị bằng 5”;

b) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số”;

c) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng 6”.

Lời giải:

Tập hợp gồm các kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp là:

A = {1; 2; 3; ...; 52}.

Tập hợp A có 52 phần tử.

a) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chữ số hàng đơn vị bằng 5” là 5; 15; 25; 35; 45. Do đó, có 5 kết quả thuận lợi cho biến cố đó.

Vậy, xác suất của biến cố đó là $\frac{5}{52}.$

b) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số” là 10; 11; 12; ...; 52. Do đó, có (52 – 10) + 1 = 43 kết quả thuận lợi cho biến cố đó.

Vậy, xác suất của biến cố đó là $\frac{43}{52}.$

c) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng 6” là 16; 23; 32. Do đó, có 3 kết quả thuận lợi cho biến cố đó.

Vậy xác suất của biến cố đó là $\frac{3}{52}.$

Bài 2 trang 30 Toán 8 Tập 2: Viết ngẫu nhiên một số tự nhiên có ba chữ số.

a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?

b) Tính xác suất của mỗi biến cố sau:

– “Số tự nhiên được viết ra là lập phương của một số tự nhiên”;

– “Số tự nhiên được viết ra là số chia hết cho 10”.

Lời giải:

a) Tập hợp số tự nhiên có ba chữ số là: {100; 101; 102; ...; 999}.

Do đó, có (999 – 100) + 1 = 900 cách viết ngẫu nhiên một số tự nhiên như vậy.

b) ⦁ Các kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là lập phương của một số tự nhiên” là 125; 216; 343; 512; 729. Do đó, có 5 kết quả thuận lợi cho biến cố đó.

Vậy, xác suất của biến cố đó là: $\frac{5}{900}=\frac{1}{180}.$

⦁ Các kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chia hết cho 10” là 100; 110; 120; …; 980; 990. Do đó, có $\frac{990-100}{10}+1=90$ kết quả thuận lợi cho biến cố đó.

Vậy xác suất của biến cố đó là: $\frac{90}{900}=\frac{1}{10}.$

Bài 3 trang 30 Toán 8 Tập 2: Sau khi tìm hiểu các tài liệu, bạn Trung lựa chọn 10 biển đẹp của các châu lục trên thế giới: Hạ Long (thuộc nước Việt Nam); Phuket (thuộc nước Thái Lan); Marasusa Tropea (thuộc nước Italia); Cala Macarella (thuộc nước Tây Ban Nha); Ifaty (thuộc nước Madagascar); Lamu (thuộc nước Kenya); Ipanema (thuộc nước Brazil); Cancun (thuộc nước Mexico); Bondi (thuộc nước Australia); Scotia (thuộc châu Nam cực). Chọn ngẫu nhiên một biển trong 10 biển đó.

a) Gọi E là tập hợp gồm các kết quả có thể xảy ra đối với biển được chọn. Tính số phần tử của tập hợp E.

b) Tính xác suất của mỗi biến cố sau:

– “Biển được chọn thuộc châu Âu”;

– “Biển được chọn thuộc châu Á”;

– “Biển được chọn thuộc châu Phi”;

– “Biển được chọn thuộc châu Úc”;

– “Biển được chọn thuộc châu Nam cực”;

– “Biển được chọn thuộc châu Mỹ”.

Lời giải:

a) Tập hợp gồm các kết quả có thể xảy ra đối với biển được chọn là E = {Hạ Long; Phuket; Marasusa Tropea; Cala Macarella; Ifaty; Lamu; Ipanema; Cancun; Bondi; Scotia}.

Tập hợp E có 10 phần tử.

b) – Các kết quả thuận lợi cho biến cố “Biển được chọn thuộc châu Âu” là Marasusa Tropea; Cala Macarella. Do đó, có 2 kết quả thuận lợi cho biến cố đó. Vậy xác suất của biến cố đó là $\frac{2}{10}=\frac{1}{5}.$

– Các kết quả thuận lợi cho biến cố “Biển được chọn thuộc châu Á” là Hạ Long; Phuket. Do đó, có 2 kết quả thuận lợi cho biến cố đó. Vậy xác suất của biến cố đó là $\frac{2}{10}=\frac{1}{5}.$

– Các kết quả thuận lợi cho biến cố “Biển được chọn thuộc châu Phi” là Ifaty; Lamu. Có 2 kết quả thuận lợi cho biến cố đó. Vậy xác suất của biến cố đó là $\frac{2}{10}=\frac{1}{5}.$

– Các kết quả thuận lợi cho biến cố “Biển được chọn thuộc châu Úc” là Bondi. Có 1 kết quả thuận lợi cho biến cố đó. Vậy xác suất của biến cố đó là $\frac{1}{10}.$

– Các kết quả thuận lợi cho biến cố “Biển được chọn thuộc châu Nam cực” là Scotia. Có 1 kết quả thuận lợi cho biến cố đó. Vậy xác suất của biến cố đó là $\frac{1}{10}.$

– Các kết quả thuận lợi cho biến cố “Biển được chọn thuộc châu Mỹ” là Ipanema; Cancun. Có 2 kết quả thuận lợi cho biến cố đó. Vậy xác suất của biến cố đó là $\frac{2}{10}=\frac{1}{5}.$

Lý thuyết Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

1. Xác suất của biến cố trong trò chơi tung đồng xu

Trong trò chơi tung đồng xu, ta có:

- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt N” bằng $\frac{1}{2}$.

- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng $\frac{1}{2}$.

2. Xác suất của biến cố trong trò chơi vòng quay số

Trong trò chơi vòng quay số đã nêu, nếu k là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng $\frac{k}{8}$.

3. Xác suất của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

Trong trò chơi ngẫu nhiên, một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.

Sơ đồ tư duy Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ

Bài 5: Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Bài tập cuối chương 6 trang 37

Bài 1: Phương trình bậc nhất một ẩn

Bài 2: Ứng dụng của phương trình bậc nhất một ẩn