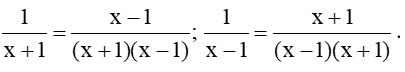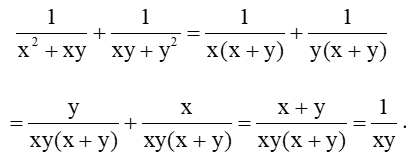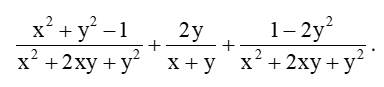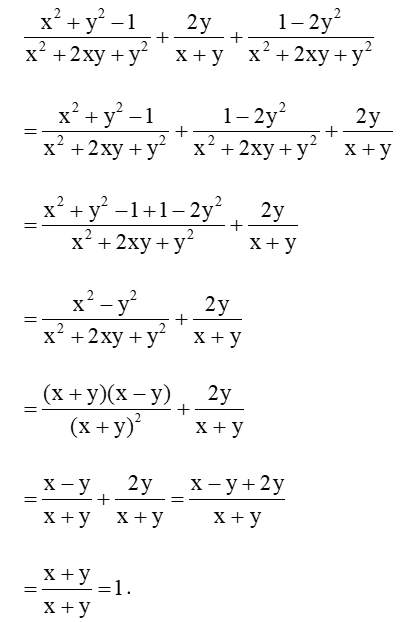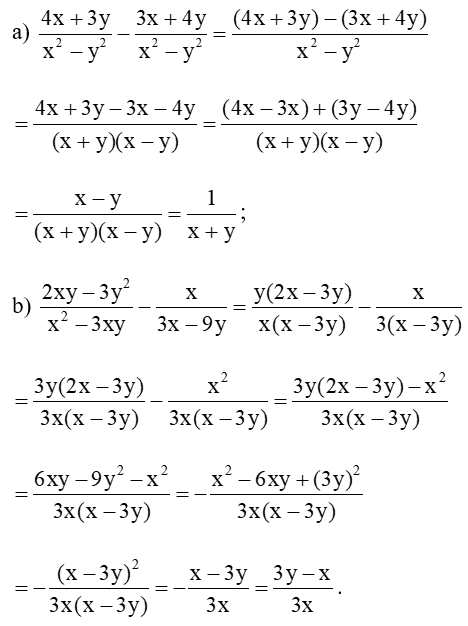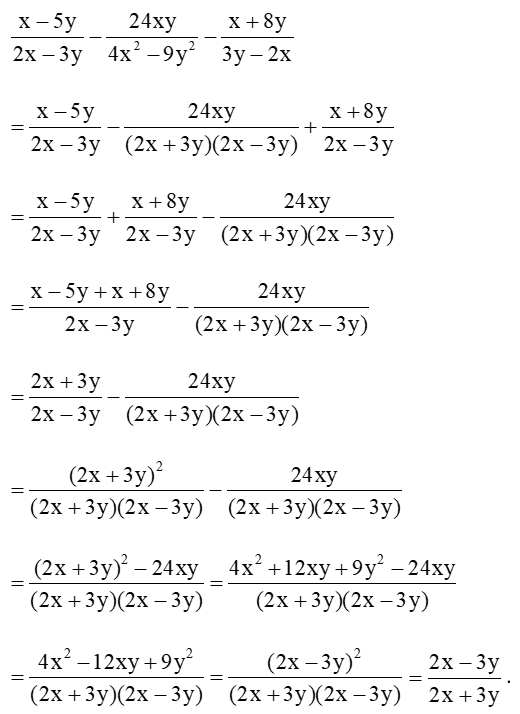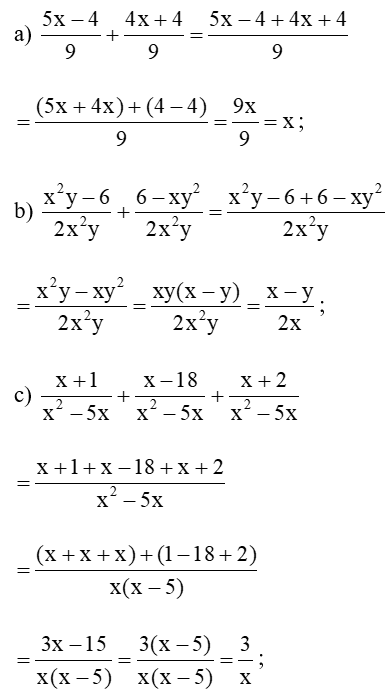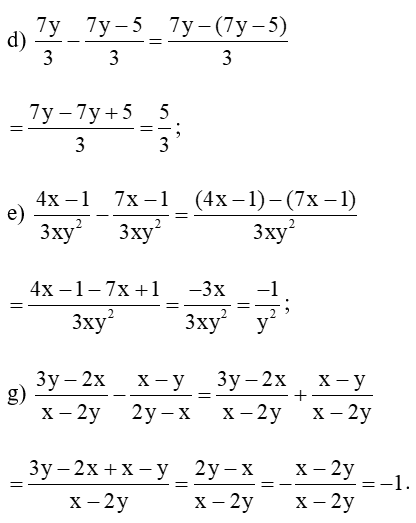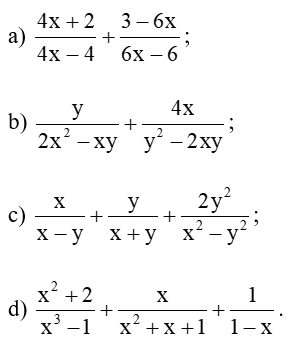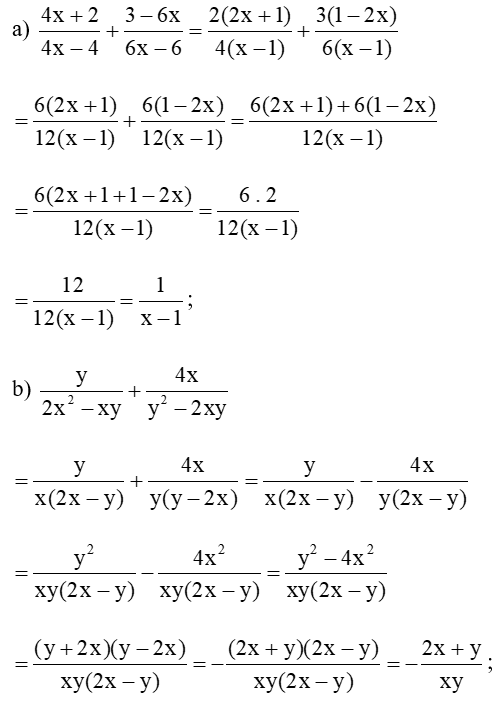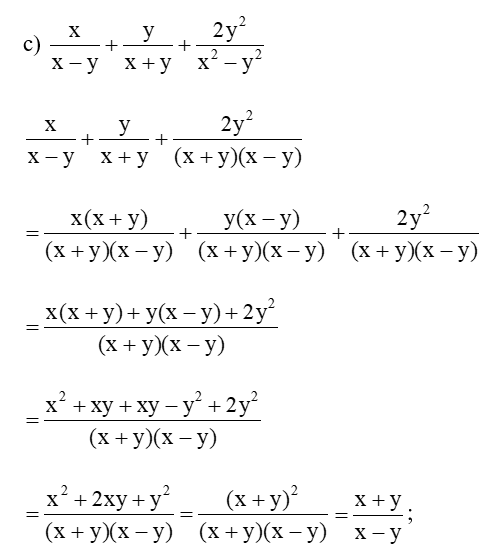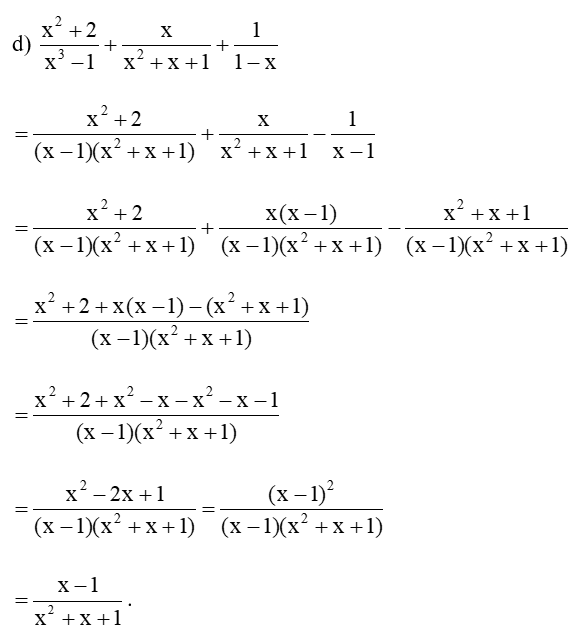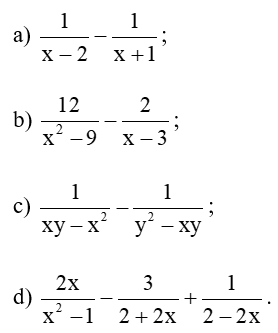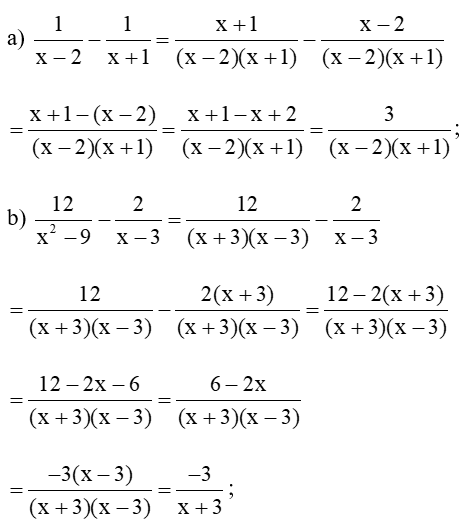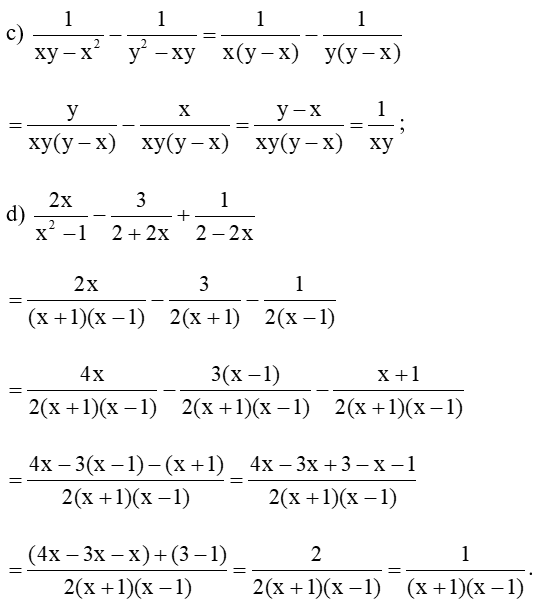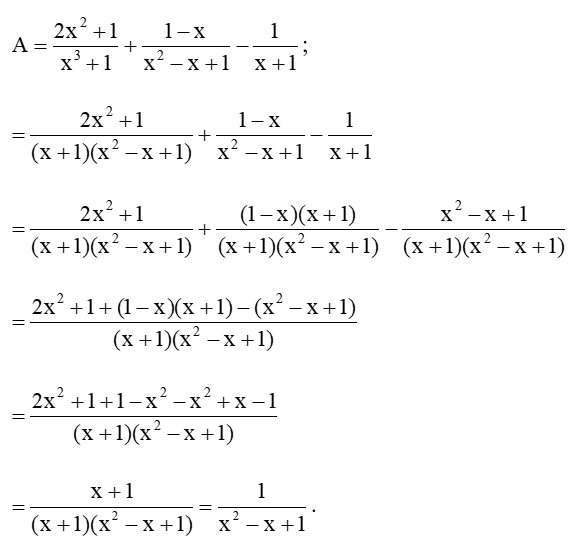Toán 8 Bài 2 (Cánh diều): Phép cộng, phép trừ phân thức đại số

Giải Toán 8 Bài 2: Phép cộng, phép trừ phân thức đại số

Bài giải Toán 8 Bài 2: Phép cộng, phép trừ phân thức đại số

Giải Toán 8 trang 38 Tập 1

Khởi động trang 38 Toán 8 Tập 1: Ở lớp 6, ta đã biết cách cộng, trừ các phân số. Làm thế nào để cộng, trừ được các phân thức đại số?

Lời giải:

Sau khi học xong bài này ta sẽ giải quyết bài toán này như sau:

Cộng, trừ được các phân thức đại số, ta thực hiện tương tự như phép cộng, phép trừ các phân số.

• Đối với các phân thức đại số có cùng mẫu thì ta thực hiện cộng (trừ) các tử và giữ nguyên mẫu.

• Đối với các phân thức đại số khác mẫu thì ta quy đồng mẫu thức các phân thức sau đó thực hiện cộng (trừ) các tử và giữ nguyên mẫu.

I. Phép cộng các phân thức đại số

Hoạt động 1 trang 38 Toán 8 Tập 1: Thực hiện phép tính: $\frac{-3}{5}+\frac{23}{5}$.

Lời giải:

Ta có $\frac{-3}{5}+\frac{23}{5}=\frac{-3+33}{5}=\frac{-30}{5}=-6$.

Luyện tập 1 trang 38 Toán 8 Tập 1: Thực hiện phép tính: $\frac{x-2y}{x^2+xy}+\frac{x+2y}{x^2+xy}$.

Lời giải:

$\frac{x-2y}{x^2+xy}+\frac{x+2y}{x^2+xy}=\frac{x-2y+x+2y}{x^2+xy}$

$=\frac{(x+x)+(2y-2y)}{x(x+y)}=\frac{2x}{x(x+y)}=\frac{2}{x+y}$.

Hoạt động 2 trang 38 Toán 8 Tập 1: Cho hai phân thức: $\frac{1}{x+1};\frac{1}{x-1}.$

a) Quy đồng mẫu thức hai phân thức trên.

b) Từ câu a, hãy thực hiện phép tính: $\frac{1}{x+1}+\frac{1}{x-1}.$

Lời giải:

a) MTC: (x + 1)(x – 1).

Quy đồng mẫu thức hai phân thức đã cho, ta được:

b) Ta có $\frac{1}{x+1}+\frac{1}{x-1}=\frac{x-1}{(x+1)(x-1)}+\frac{x+1}{(x-1)(x+1)}$

$=\frac{x-1+x+1}{(x+1)(x-1)}=\frac{2x}{(x+1)(x-1)}$.

Giải Toán 8 trang 39 Tập 1

Luyện tập 2 trang 39 Toán 8 Tập 1: Thực hiện phép tính: $\frac{1}{x^2+xy}+\frac{1}{xy+y^2}$

Lời giải:

Ta có

Hoạt động 3 trang 39 Toán 8 Tập 1: Hãy nêu các tính chất của phép cộng phân số.

Lời giải:

Phép cộng phân số có các tính chất: giao hoán, kết hợp, cộng với 0.

Với các số a, b, c, d, e, g (b, d, g ≠ 0), ta có:

• Giao hoán: $\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}$;

• Kết hợp: $\left(\frac{a}{b}+\frac{c}{d}\right)+\frac{e}{g}=\frac{a}{b}+\left(\frac{c}{d}+\frac{e}{g}\right)$;

• Cộng với 0: $\frac{a}{b}+0=0+\frac{a}{b}=\frac{a}{b}$.

Luyện tập 3 trang 39 Toán 8 Tập 1: Tính một cách hợp lí:

Lời giải:

II. Phép trừ các phân thức đại số

Giải Toán 8 trang 41 Tập 1

Luyện tập 4 trang 41 Toán 8 Tập 1: Thực hiện phép tính:

a) $\frac{4x+3y}{x^2-y^2}-\frac{3x+4y}{x^2-y^2}$;

b) $\frac{2xy-3y^2}{x^2-3xy}-\frac{x}{3x-9y}$.

Lời giải:

Giải Toán 8 trang 42 Tập 1

Luyện tập 5 trang 42 Toán 8 Tập 1: Tính một cách hợp lí: $\frac{x-5y}{2x-3y}-\frac{24xy}{4x^2-9y^2}-\frac{x+8y}{3y-2x}$.

Lời giải:

Bài tập

Bài 1 trang 42 Toán 8 Tập 1: Thực hiện phép tính:

a) $\frac{5x-4}{9}+\frac{4x+4}{9}$;

b) $\frac{x^{2}y-6}{2x^{2}y}+\frac{6-x{y}^2}{2x^{2}y}$;

c) $\frac{x+1}{x^2-5x}+\frac{x-18}{x^2-5x}+\frac{x+2}{x^2-5x}$;

d) $\frac{7y}{3}-\frac{7y-5}{3}$;

e) $\frac{4x-1}{3x{y}^2}-\frac{7x-1}{3x{y}^2}$;

g) $\frac{3y-2x}{x-2y}-\frac{x-y}{2y-x}$.

Lời giải:

Bài 2 trang 42 Toán 8 Tập 1: Thực hiện phép tính:

Lời giải:

Bài 3 trang 42 Toán 8 Tập 1: Thực hiện phép tính:

Lời giải:

Giải Toán 8 trang 43 Tập 1

Bài 4 trang 43 Toán 8 Tập 1:

a) Rút gọn biểu thức: $A=\frac{2x^2+1}{x^3+1}+\frac{1-x}{x^2-x+1}-\frac{1}{x+1}$;

b) Tính giá trị của biểu thức A tại x = −3.

Lời giải:

a) Rút gọn biểu thức A như sau:

b) Điều kiện xác định của phân thức $\frac{1}{x^2-x+1}$ là x² – x +1 ≠ 0.

b) Với x = −3 ta thấy x² – x +1 = (−3)² − (−3) +1 = 9²+ 9 + 1 = 81 + 10 = 91 ≠ 0.

Do đó, giá trị của biểu thức A tại x = −3 là:

$\frac{1}{{(-3)}^2-(-3)+1}=\frac{1}{91}$.

Bài 5 trang 43 Toán 8 Tập 1: Một xí nghiệp dự định sản xuất 10 000 sản phẩm trong x ngày. Khi thực hiện, xí nghiệp đã làm xong sớm hơn 1 ngày so với dự định và còn làm thêm được 80 sản phẩm. Viết phân thức biểu thị theo x:

a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định;

b) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế;

c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày theo dự định.

Lời giải:

a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là: $\frac{10000}{x}$ (sản phẩm).

b) Số sản phẩm xí nghiệp đã hoàn thành trên thực tế là:

10 000 + 80 = 10 080 (sản phẩm)

Số ngày xí nghiệp đã hoàn thành trên thực tế là: x – 1 (ngày)

Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế là: $\frac{10080}{x-1}$ (sản phẩm)

c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là:

$\frac{10000}{x}-\frac{10080}{x-1}=80\left(\frac{125}{x}-\frac{126}{x-1}\right)$$=80\left(\frac{125(x-1)}{x(x-1)}-\frac{126x}{x(x-1)}\right)$

$=80.\frac{125x-125-126x}{x(x-1)}=\frac{-80x-10000}{x(x-1)}$ (sản phẩm).

Bài 6 trang 43 Toán 8 Tập 1: Người ta mở hai vòi nước cùng chảy vào bể không chứa nước. Thời gian để vòi thứ nhất chảy một mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ. Gọi x (giờ) là thời gian vòi thứ nhất chảy một mình để đầy bể. Viết phân thức biểu thị theo x:

a) Thời gian vòi thứ hai chảy một mình đầy bể;

b) Phần bể mà mỗi vòi chảy được trong 1 giờ;

c) Phần bể mà cả hai vòi chảy được trong 1 giờ.

Lời giải:

a) Theo đề bài, thời gian để vòi thứ nhất chảy một mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ.

Hay thời gian để vòi thứ hai chảy một mình đầy bể nhiều hơn thời gian để vòi thứ nhất chảy một mình đầy bể là 2 giờ.

Do đó, thời gian vòi thứ hai chảy một mình đầy bể là: x + 2 (giờ).

b) Số phần bể mà vòi thứ nhất chảy được trong 1 giờ là $\frac{1}{x}$ (bể)

Số phần bể mà vòi thứ hai chảy được trong 1 giờ là $\frac{1}{x+2}$ (bể)

c) Số phần bể mà cả hai vòi chảy được trong 1 giờ là:

$\frac{1}{x}+\frac{1}{x+2}=\frac{x+2}{x(x+2)}+\frac{x}{x(x+2)}$

$=\frac{x+2+x}{x(x+2)}=\frac{2x+2}{x(x+2)}$ (bể).

Bài 7 trang 43 Toán 8 Tập 1: Để hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng 120 cây xanh. Khi bắt đầu thực hiện, chi đoàn được tăng cường thêm 3 đoàn viên. Gọi x là số đoàn viên ban đầu của chi đoàn và giả sử số cây mỗi đoàn viên trồng là như nhau. Viết phân thức biểu thị theo x:

a) Số cây mỗi đoàn viên trồng theo dự định;

b) Số cây mỗi đoàn viên trồng theo thực tế;

c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế.

Lời giải:

a) Theo dự định, chi đoàn thanh niên trồng 120 cây xanh, ban đầu chi đoàn có x đoàn viên.

Do đó, phân thức biểu thị số cây mỗi đoàn viên trồng theo dự định là $\frac{120}{x}$ (cây).

b) Theo thực tế, chi đoàn được tăng cường thêm 3 đoàn viên.

Khi đó, số đoàn viên của chi đoàn theo thực tế là: x + 3 (đoàn viên).

Do đó, phân thức biểu thị số cây mỗi đoàn viên trồng theo thực tế là $\frac{120}{x+3}$ (cây).

c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế là:

$\frac{120}{x}-\frac{120}{x+3}=\frac{120(x+3)-120x}{x(x+3)}$

$=\frac{120x+360-120x}{x(x+3)}=\frac{360}{x(x+3)}$ (cây).

Vậy phân thức biểu thị số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế là $\frac{360}{x(x+3)}$ (cây).

Bài 8 trang 43 Toán 8 Tập 1: Gia đình cô Lương nuôi ba con lợn. Cả ba con lợn đều ăn cùng một loại thức ăn gia súc. Biểu đồ cột ở Hình 2 biểu diễn số ngày mà mỗi con lợn ăn hết một bao thức ăn. Hỏi cả ba con lợn ăn trong x ngày (x∈ ℕ*) thì cần bao nhiêu thức ăn?

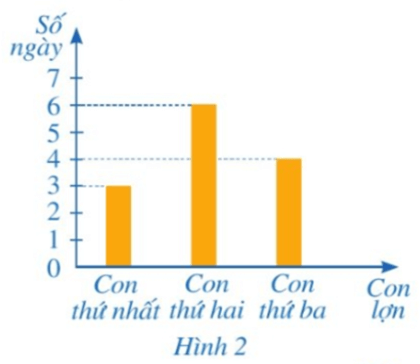
Lời giải:

Trên biểu đồ Hình 2 có:

• Con lợn thứ nhất ăn 3 ngày hết 1 bao thức ăn.

Khi đó, mỗi ngày con lợn thứ nhất ăn hết $\frac{1}{3}$ bao thức ăn.

Do đó, con lợn thứ nhất ăn trong x ngày hết $\frac{x}{3}$ bao thức ăn.

• Con lợn thứ hai ăn 6 ngày hết 1 bao thức ăn.

Khi đó, mỗi ngày con lợn thứ hai ăn hết $\frac{1}{6}$ bao thức ăn.

Do đó, con lợn thứ hai ăn trong x ngày hết $\frac{x}{6}$ bao thức ăn.

• Con lợn thứ ba ăn 4 ngày hết 1 bao thức ăn.

Khi đó, mỗi ngày con lợn thứ hai ăn hết $\frac{1}{4}$ bao thức ăn.

Do đó, con lợn thứ hai ăn trong x ngày hết $\frac{x}{4}$ bao thức ăn.

Cả ba con lợn ăn trong x ngày (x ∈ ℕ*) thì cần:

$\frac{x}{3}+\frac{x}{6}+\frac{x}{4}=\frac{4x}{12}+\frac{2x}{12}+\frac{3x}{12}=\frac{9x}{12}=\frac{3x}{4}$ (bao thức ăn).

Vậy cả ba con lợn ăn trong x ngày (x ∈ ℕ*) thì cần $\frac{3x}{4}$ bao thức ăn.

Bài giảng Toán 8 Bài 2: Phép cộng, phép trừ phân thức đại số

Lý thuyết Phép cộng, phép trừ phân thức đại số

1. Cộng, trừ hai phân thức cùng mẫu

Muốn cộng (hoặc trừ) hai phân thức có cùng mẫu thức, ta cộng (hoặc trừ) các tử thức với nhau và giữ nguyên mẫu thức.

$\frac{A}{B}+\frac{C}{B}=\frac{A+C}{B};\frac{A}{B}-\frac{C}{B}=\frac{A-C}{B}$

Chú ý: Phép cộng phân thức có các tính chất giao hoán, kết hợp tương tự như đối với phân số.

Ví dụ:

$\begin{array}{l}\frac{x+y}{xy}+\frac{x-y}{xy}=\frac{x+y+x-y}{xy}=\frac{2x}{xy}=\frac{2}{y}\\ \frac{x}{x+3}+\frac{2-x}{x+3}=\frac{x+2-x}{x+3}=\frac{2}{x+3}\end{array}$

2. Cộng, trừ hai phân thức khác mẫu

Quy đồng mẫu thức hai phân thức

Quy đồng mẫu thức hai phân thức là biến đổi hai phân thức đã cho thành hai phân thức mới có cùng mẫu thức và lần lượt bằng hai mẫu thức đã cho.

Mẫu thức chung

Mẫu thức của các phân thức mới đó gọi là mẫu thức chung của hai phân thức đã cho.

Cộng, trừ hai phân thức khác mẫu

Muốn cộng, trừ hai phân thức khác mẫu thức, ta thực hiện các bước:

- Quy đồng mẫu thức;

- Cộng, trừ các phân thức có cùng mẫu thức vừa tìm được.

Chú ý:

a. Phép cộng các phân thức cũng có các tính chất giao hoán, kết hợp:

$\frac{A}{B}+\frac{C}{D}=\frac{C}{D}+\frac{A}{B};\left(\frac{A}{B}+\frac{C}{D}\right)+\frac{E}{F}=\frac{A}{B}+\left(\frac{C}{D}+\frac{E}{F}\right)$.

b. Phân thức đối của phân thức $\frac{A}{B}$ là $-\frac{A}{B}$. Ta có tính chất $-\frac{A}{B}=\frac{-A}{B}=\frac{A}{-B}$.

c. Phép trừ phân thức có thể chuyển thành phép cộng với phân thức đối: $\frac{A}{B}-\frac{C}{D}=\frac{A}{B}+\left(-\frac{C}{D}\right)$

Xem thêm lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 1: Phân thức đại số

Bài 2: Phép cộng, phép trừ phân thức đại số

Bài 3: Phép nhân, phép chia phân thức đại số

Bài tập cuối chương 2

Hoạt động thực hành và trải nghiệm Chủ đề 1: Quản lí tài chính cá nhân