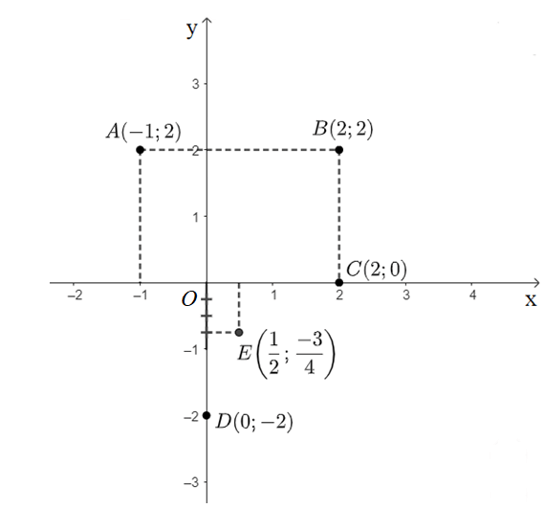Toán 8 Bài 2 (Cánh diều): Mặt phẳng tọa độ. Đồ thị của hàm số

Giải Toán 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

Bài giải Toán 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

Giải Toán 8 trang 60 Tập 1

Khởi động trang 60 Toán 8 Tập 1: Ở lớp 6, ta đã biết rằng mỗi điểm trên bản đồ địa lí được xác định bởi một cặp gồm hai con số (tọa độ địa lí) là kinh độ và vĩ độ. Chẳng hạn, tọa độ địa lí của hồ Hoàn Kiếm ở Thủ đô Hà Nội là: (21°01’B; 105°51’Đ).

Trong toán học, cặp số để xác định vị trí của một điểm trên mặt phẳng được gọi là gì?

Lời giải:

Sau khi học xong bài này ta sẽ giải quyết bài toán này như sau:

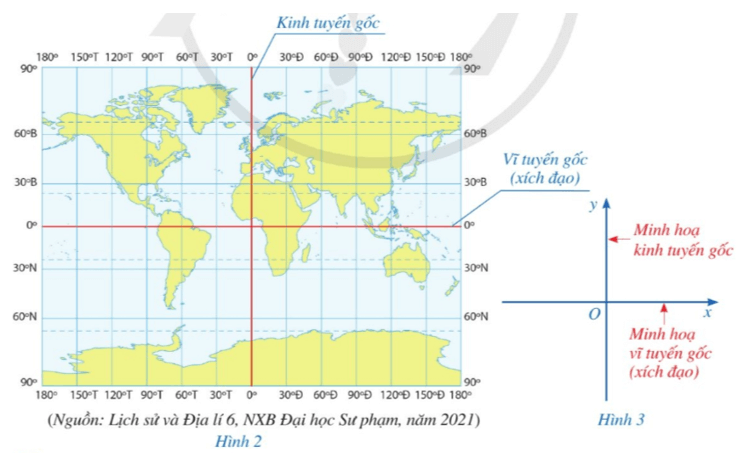
Mỗi điểm trên bản đồ địa lí được xác định bởi một cặp gồm hai con số (tọa độ địa lí) là kinh độ và vĩ độ.

Trong toán học, cặp số để xác định vị trí của một điểm trên mặt phẳng được gọi tọa độ.

I. Mặt phẳng tọa độ

Hoạt động 1 trang 60 Toán 8 Tập 1: Hình 2 là một dạng phép chiếu bản đồ có các đường kinh tuyến và vĩ tuyến đều là các đường thẳng, trong đó kinh tuyến gốc và vĩ tuyến gốc được minh họa bằng hai đường thẳng màu đỏ. Chúng được biểu diễn bởi hai trục Ox, Oy trên mặt phẳng ở Hình 3. Nêu nhận xét về hai trục Ox, Oy.

Lời giải:

Hai đường thẳng màu đỏ trong Hình 2 được biểu diễn bởi hai trục Ox, Oy trên mặt phẳng ở Hình 3.

Khi đó, hai trục Ox, Oy trong Hình 3 vuông góc với nhau.

Giải Toán 8 trang 61 Tập 1

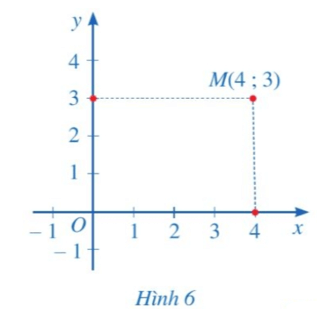
Hoạt động 2 trang 61 Toán 8 Tập 1: Cho điểm M trong mặt phẳng tọa độ Oxy (Hình 6).

a) Hình chiếu của điểm M trên trục hoành Ox là điểm nào trên trục số Ox?

b) Hình chiếu của điểm M trên trục tung Oy là điểm nào trên trục số Oy?

Lời giải:

Quan sát Hình 6, ta thấy:

a) Hình chiếu của điểm M trên trục hoành Ox là điểm 4 trên trục số Ox.

b) Hình chiếu của điểm M trên trục tung Oy là điểm 3 trên trục số Oy.

Giải Toán 8 trang 62 Tập 1

Luyện tập 1 trang 62 Toán 8 Tập 1: Trong mặt phẳng tọa độ Oxy, hãy nêu cách xác định các điểm

$A(-1;2);B(2;2);C(2;0);D(0;-2);E\left(\frac{1}{2};-\frac{3}{4}\right).$

Lời giải:

Cách xác định các điểm trong mặt phẳng tọa độ Oxy là:

• Xác định điểm A(− 1; 2):

Qua điểm – 1 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm A(− 1; 2).

• Xác định điểm B(2; 2):

Qua điểm 2 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm B(2; 2).

• Xác định điểm C(2; 0):

Qua điểm 2 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Đường thẳng thẳng này cắt trục Ox tại điểm C(2; 0).

• Cách xác định điểm D(0; − 2):

Qua điểm − 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Đường thẳng thẳng này cắt trục Oy tại điểm D(0; − 2).

• Xác định điểm $E\left(\frac{1}{2};-\frac{3}{4}\right)$:

Qua điểm $\frac{1}{2}$ trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm $\frac{-3}{4}$ trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm $E\left(\frac{1}{2};-\frac{3}{4}\right)$.

Từ đó ta xác định các điểm

$A(-1;2);B(2;2);C(2;0);D(0;-2);E\left(\frac{1}{2};-\frac{3}{4}\right)$ trên trục số như sau:

Hoạt động 3 trang 62 Toán 8 Tập 1: Nhiệt độ dự báo thấp nhất y (°C) ở thành phố Đà Lạt là một hàm số theo thời điểm x (h) trong ngày 14/4/2022. Hàm số này được biểu thị dưới dạng Bảng 1.

Lời giải:

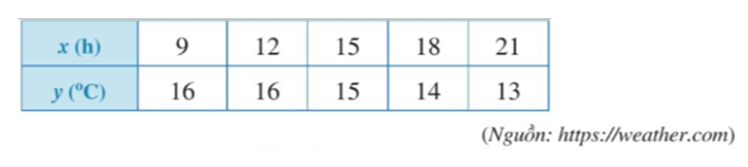
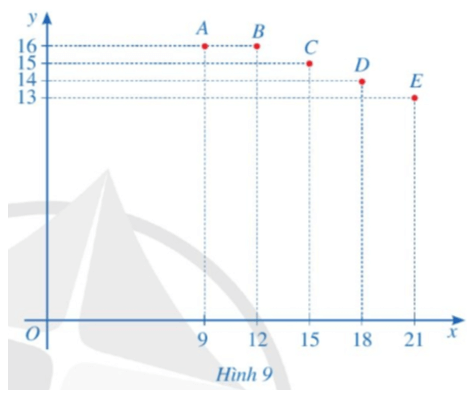
Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm có tọa độ là các cặp số (x; y) tương ứng ở Bảng 1 là: A(9; 16); B(12; 16); C(15; 15); D(18; 14); E(21; 13).

Ta biểu diễn các điểm trên mặt phẳng tọa độ như sau:

Giải Toán 8 trang 63 Tập 1

Hoạt động 4 trang 63 Toán 8 Tập 1: Xét hàm số y = 2x.

a) Tính các giá trị y₁, y₂, y₃ tương ứng với các giá trị $x_1=-\mathrm{1,}{x}_2=\mathrm{1,}{x}_3=\frac{3}{2}.$

b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm M₁(x₁; y₁); M₂(x₂; y₂); M₃(x₃; y₃).

Lời giải:

a) • Với x₁ = −1, ta có: y₁ = 2 . (−1) = −2;

• Với x₂ = 1, ta có: y₂ = 2 . 1 = 2;

• Với $x_3=\frac{3}{2}$, ta có: $y_3=2.\frac{3}{2}=3$.

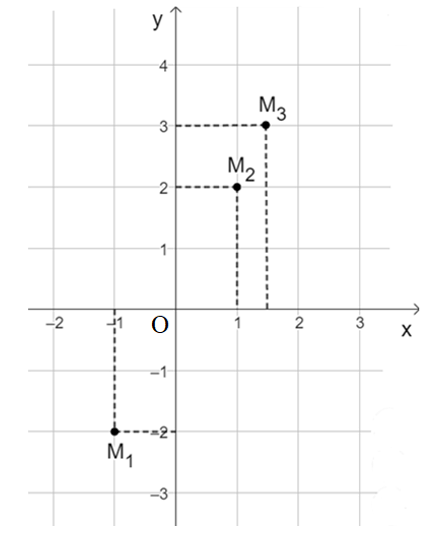
b) Ta có M₁(−1; −2); M₂(1; 2); $M_3\left(\frac{3}{2};3\right)$.

• Xác định điểm M₁(−1; −2):

Qua điểm – 1 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm − 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm M₁(−1; −2).

• Xác định điểm M₂(1; 2):

Qua điểm 1 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm M₂(1; 2).

• Xác định điểm $M_3\left(\frac{3}{2};3\right)$:

Qua điểm $\frac{3}{2}$ trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm 3 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm $M_3\left(\frac{3}{2};3\right)$.

Biểu diễn các điểm M₁; M₂; M₃ trong mặt phẳng tọa độ Oxy như sau:

Giải Toán 8 trang 64 Tập 1

Luyện tập 2 trang 64 Toán 8 Tập 1: Số lượng sản phẩm bán được y (nghìn sản phẩm) là một hàm số theo thời gian x (tháng). Hàm số này được biểu thị dưới dạng Bảng 2.

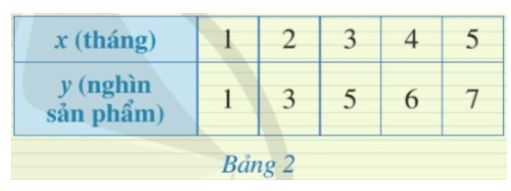
Trong mặt phẳng tọa độ Oxy, hai điểm A(2; 3), B(5; 6) có thuộc đồ thị của hàm số hay không? Vì sao?

Lời giải:

Quan sát Bảng 2, ta thấy:

• Với x = 2 thì y = 3 nên điểm A(2; 3) thuộc đồ thị hàm số;

• Với x = 5 thì y = 7 nên điểm B(5; 6) không thuộc đồ thị hàm số.

Vậy trong mặt phẳng tọa độ Oxy, hai điểm A(2; 3), B(5; 6) không thuộc đồ thị của hàm số.

Bài tập

Bài 1 trang 64 Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Điểm thuộc trục hoành có tung độ bằng 0.

b) Điểm thuộc trục hoành có hoành độ bằng 0.

c) Điểm thuộc trục tung có tung độ bằng 0.

d) Điểm thuộc trục tung có hoành độ bằng 0.

Lời giải:

• Các điểm nằm trên trục hoành đều có tung độ bằng 0 nên khẳng định a) đúng.

• Các điểm nằm trên trục hoành thì điểm đó có tọa độ (a; 0) với a là giá trị bất kì.

Do đó khẳng định b) sai.

• Các điểm nằm trên trục tung thì điểm đó có tọa độ (0; b) với b là giá trị bất kì.

Do đó khẳng định c) sai.

• Các điểm nằm trên trục tung đều có hoành độ bằng 0 nên khẳng định d) đúng.

Bài 2 trang 64 Toán 8 Tập 1: Điểm M(a; b) thuộc góc phần tư nào trong mỗi trường hợp sau?

a) a > 0, b > 0.

b) a > 0, b < 0.

c) a < 0, b > 0.

d) a < 0, b < 0.

Lời giải:

a) Với a > 0, b > 0 thì điểm M(a; b) thuộc góc phần tư thứ nhất.

b) Với a > 0, b < 0 thì điểm M(a; b) thuộc góc phần tư thứ tư.

c) Với a < 0, b > 0 thì điểm M(a; b) thuộc góc phần tư thứ hai.

d) Với a < 0, b < 0 thì điểm M(a; b) thuộc góc phần tư thứ ba.

Bài 3 trang 64 Toán 8 Tập 1: Xác định tọa độ điểm A trong mỗi trường hợp sau:

a) Hoành độ bằng – 3 và tung độ bằng 5;

b) Hoành độ bằng – 2 và nằm trên trục hoành;

c) Tung độ bằng – 4 và nằm trên trục tung.

Lời giải:

a) Điểm A có hoành độ bằng – 3 và tung độ bằng 5 nên tọa độ điểm A là A(– 3; 5);

b) Điểm A có hoành độ bằng –2 và nằm trên trục hoành nên tọa độ điểm A là A(– 2; 0);

c) Điểm A có tung độ bằng – 4 và nằm trên trục tung nên tọa độ điểm A là A(0; – 4).

Giải Toán 8 trang 65 Tập 1

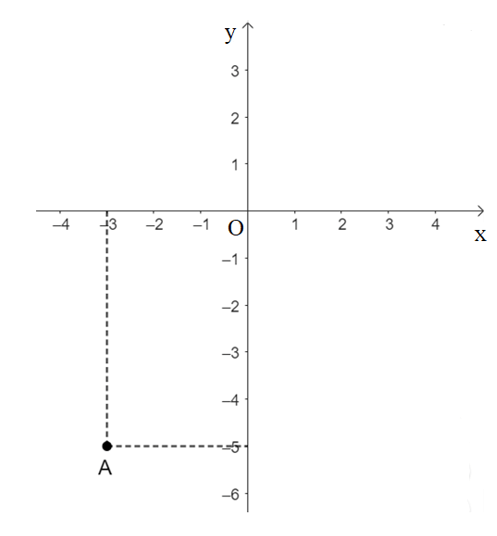
Bài 4 trang 65 Toán 8 Tập 1: Trong mặt phẳng tọa độ Oxy, nêu cách xác định điểm A(– 3; – 5).

Lời giải:

Xác định điểm A(– 3; – 5):

Qua điểm – 3 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.

Qua điểm − 5 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.

Hai đường thẳng trên cắt nhau tại điểm A(– 3; – 5).

Điểm A biểu diễn trên mặt phẳng tọa độ như sau:

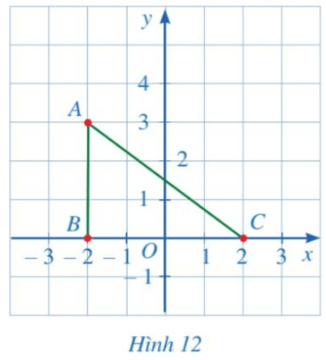
Bài 5 trang 65 Toán 8 Tập 1: Cho tam giác ABC như Hình 12.

a) Xác định tọa độ các điểm A, B, C.

b) Tam giác ABC có là tam giác vuông hay không?

c) Xác định tọa độ điểm D để tứ giác ABCD là hình chữ nhật.

Lời giải:

a) Dóng các điểm A, B, C lên hai trục Ox, Oy ta có tọa độ các điểm A, B, C là A(– 2; 3), B(– 2; 0), C(2; 0).

b) Hình chiếu của điểm A trên trục hoành là điểm – 2 trên trục Ox.

Mà điểm B cũng có hoành độ bằng – 2 nên AB ⊥ BC.

Tam giác ABC có $\widehat{ABC}=90°$ (vì AB ⊥ BC) nên tam giác ABC vuông tại A.

c) Tam giác ABC có $\widehat{ABC}=90°$ nên để tứ giác ABCD là hình chữ nhật thì $\widehat{DAB}=90°;\widehat{DCB}=90°$ hay AB ⊥ AD; BC ⊥ CD.

• Qua điểm A, ta kẻ đường thẳng vuông góc với trục Oy.

• Qua điểm C, ta kẻ đường thẳng vuông góc với trục Ox.

Hai đường thẳng này cắt nhau tại điểm D.

• AD cắt trục Oy tại điểm 3 nên điểm D có tung độ bằng 3.

• CD cắt trục Ox tại điểm 2 nên điểm D có hoành độ bằng 2.

Do đó, tọa điểm D là D(2; 3).

Bài 6 trang 65 Toán 8 Tập 1: Nhập cụm từ “chợ Bến Thành” trên trang http://google.com/maps, sau đó nháy chuột vào địa điểm đó trên bản đồ ta được thông tin về kinh độ, vĩ độ như Hình 13. Hãy viết tọa độ địa lí của chợ Bến Thành thuộc Thành phố Hồ Chí Minh.

Lời giải:

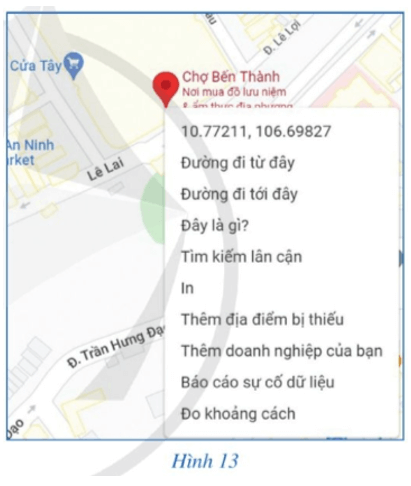
Thực hiện các bước theo yêu cầu bài toán ta được thông tin về kinh độ, vĩ độ. Do đó, tọa độ địa lí của chợ Bến Thành thuộc Thành phố Hồ Chí Minh là (10,77211; 106,69827).

Bài 7 trang 65 Toán 8 Tập 1: Nhiệt độ dự báo tại một số thời điểm trong ngày 25/5/2022 ở Thành phố Hồ Chí Minh được cho bởi Hình 14.

a) Viết hàm số dạng bảng biểu thị nhiệt độ dự báo y (°C) tại thời điểm x (h) ở Thành phố Hồ Chí Minh.

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm có tọa độ là các cặp số (x; y) tương ứng ở bảng đã viết ở câu a.

c) Trong mặt phẳng tọa độ Oxy, điểm M(15; 24) có thuộc đồ thị của hàm số cho bởi bảng trên hay không? Vì sao?

Lời giải:

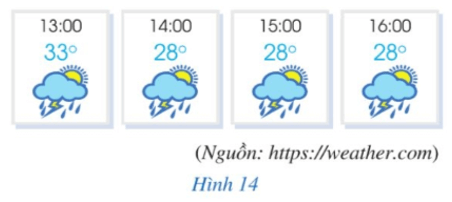
a) Quan sát Hình 14, ta thấy:

• Tại x = 13 h thì y = 33°C;

• Tại x = 14 h thì y = 28°C;

• Tại x = 15 h thì y = 28°C;

• Tại x = 16 h thì y = 28°C;

Hàm số dạng bảng biểu thị nhiệt độ dự báo y (°C) tại thời điểm x (h) ở Thành phố Hồ Chí Minh như sau:

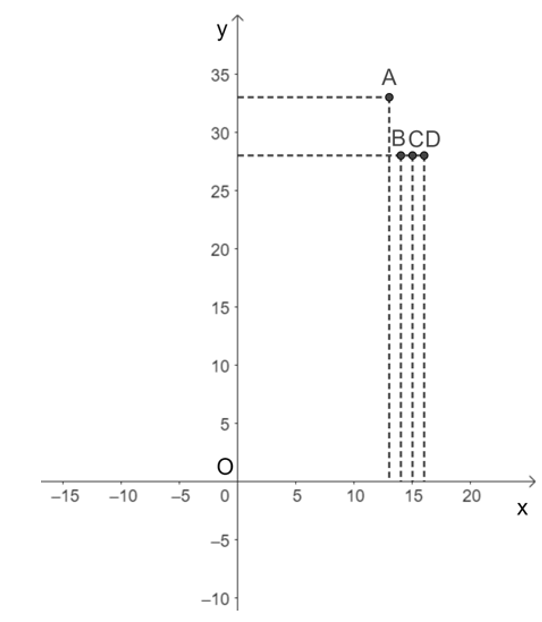
b) Ta biểu diễn các điểm A(13; 33); B(14; 28); C(15; 28); D(16; 28) trong mặt phẳng tọa độ Oxy như sau:

c) Theo bảng biểu diễn ở câu a: khi x = 15 thì y = 28.

Do đó, điểm M(15; 24) không thuộc đồ thị của hàm số.

Lý thuyết Mặt phẳng tọa độ. Đồ thị của hàm số

1. Mặt phẳng tọa độ

Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có trục tọa độ Oxy.

Trục Ox, Oy gọi là các trục tọa độ. Ox là trục hoành, Oy là trục tung. O là gốc tọa độ.

Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng Oxy.

Chú ý. Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau.

2. Tọa độ của một điểm trong mặt phẳng tọa độ

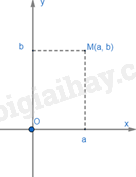
Cho điểm M nằm trong mặt phẳng tọa độ.

Giả sử hình chiếu của điểm M lên Ox là điểm a, lên Oy là điểm b. Cặp số (a;b) gọi là tọa độ của điểm M, a là hoành độ, b là tung độ.

Điểm M có tọa độ (a; b) kí hiệu là M(a; b).

3. Độ thị của hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x;f(x)) trên mặt phẳng tọa độ.

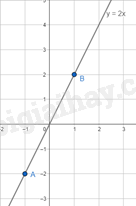
Ví dụ: Xét hàm số y = 2x

Giá trị $y_1;y_2$ tương ứng với $x_1=-1;x_2=1$ là: $y_1=2.(-1)=-2;y_2^{}=2.1=2$

Hàm số y = 2x có đồ thị như sau:

Xem thêm lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số bậc nhất y = ax + b (a khác 0)

Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0)

Bài tập cuối chương 3

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều