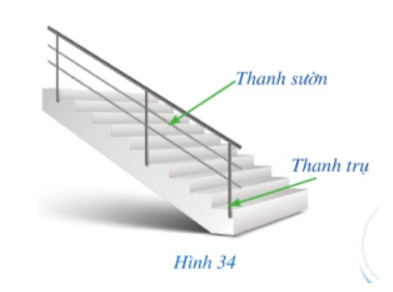
Toán 8 Bài 4 (Cánh diều): Hình bình hành

Giải Toán 8 Bài 4: Hình bình hành

Bài giải Toán 8 Bài 4: Hình bình hành

Giải Toán 8 trang 105 Tập 1

Khởi động trang 105 Toán 8 Tập 1: Trong thiết kế tay vịn cầu thang (Hình 34), người ta thường để các cặp thanh sườn song song với nhau, các cặp thanh trụ song song với nhau, tạo nên các hình bình hành.

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

‒ Hình bình hành có:

+ Các cạnh đối song song và bằng nhau;

+ Các góc đối bằng nhau;

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

‒ Dấu hiệu nhận biết hình bình hành:

+ Tứ giác có các cặp cạnh đối song song với nhau là hình bình hành.

+ Tứ giác có các cặp cạnh đối bằng nhau là hình bình hành.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Tứ giác có các cặp góc đối bằng nhau là hình bình hành.

I. Định nghĩa

Hoạt động 1 trang 105 Toán 8 Tập 1: Cho biết các cặp cạnh đối AB và CD, AD và BC của tứ giác ABCD ở Hình 35 có song song với nhau hay không.

Lời giải:

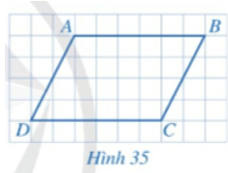
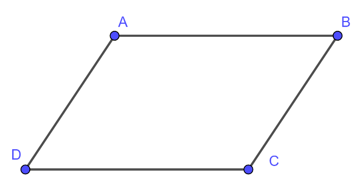
Tứ giác ABCD ở Hình 35 có các cặp cạnh đối AB // CD, AD // BC.

II. Tính chất

Giải Toán 8 trang 106 Tập 1

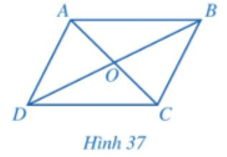
Hoạt động 2 trang 106 Toán 8 Tập 1: Cho hình bình hành ABCD (Hình 37).

a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.

b) So sánh các cặp góc: $\widehat{DAB}$ và $\widehat{BCD}$; $\widehat{ABC}$ và $\widehat{CDA}$.

c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD và AD // BC.

Vì AB // CD nên $\widehat{ABD}=\widehat{CDB}$ (so le trong).

Vì AD // BD nên $\widehat{ADB}=\widehat{CBD}$ (so le trong)

Xét ΔABD và ΔCDB có:

$\widehat{ABD}=\widehat{CDB}$ (chứng minh trên);

BD là cạnh chung;

$\widehat{ADB}=\widehat{CBD}$ (chứng minh trên)

Do đó ΔABD = ΔCDB (g.c.g)

Suy ra AB = CD và DA = BC (các cặp cạnh tương ứng).

b) Do ΔABD = ΔCDB (câu a) nên $\widehat{DAB}=\widehat{BCD}$ (cặp góc tương ứng)

Chứng minh tương tự câu a ta cũng có ΔABC = ΔCDA (g.c.g)

Suy ra $\widehat{ABC}=\widehat{CDA}$ (cặp góc tương ứng).

c) Xét ΔOAB và ΔOCD có:

$\widehat{OAB}=\widehat{OCD}$ (do AB // CD);

AB = CD (theo câu a);

$\widehat{OBA}=\widehat{ODC}$ (do AB // CD).

Do đó ΔOAB = ΔOCD (g.c.g)

Suy ra OA = OC và OB = OD (các cặp cạnh tương ứng).

Luyện tập 1 trang 106 Toán 8 Tập 1: Cho hình bình hành ABCD có $\widehat{A}=80°$, AB = 4 cm, BC = 5 cm. Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.

Lời giải:

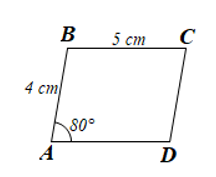
Do ABCD là hình bình hành nên ta có:

• CD = AB = 4 cm;

• AD = BC = 5 cm;

• $\widehat{C}=\widehat{A}=80°$;

• $\widehat{B}=\widehat{D}$

Mặt khác BC // AD (do ABCD là hình bình hành)

Nên $\widehat{A}+\widehat{B}=180°$ (hai góc trong cùng phía)

Suy ra $\widehat{B}=180°-\widehat{A}=180°-80°=100°$

Do đó $\widehat{D}=\widehat{B}=100°$.

III. Dấu hiệu nhận biết

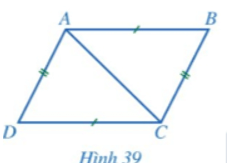
Hoạt động 3 trang 106, 107 Toán 8 Tập 1: a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39).

• Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: $\widehat{BAC}$ và $\widehat{DCA}$; $\widehat{ACB}$ và $\widehat{CAD}$.

• ABCD có phải là hình bình hành hay không?

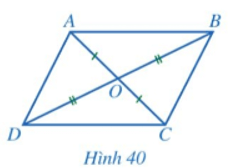
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40).

• Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: $\widehat{BAC}$ và $\widehat{DCA}$; $\widehat{ACB}$ và $\widehat{CAD}$.

• ABCD có phải là hình bình hành hay không?

Lời giải:

a) • Xét ΔABC và ΔCDA có:

AB = CD (giả thiết); BC = DA (giả thiết); AC là cạnh chung

Do đó ΔABC = ΔCDA (c.c.c)

Suy ra $\widehat{BAC}=\widehat{DCA}$ và $\widehat{ACB}=\widehat{CAD}$ (các cặp góc tương ứng).

• Ta có $\widehat{BAC}=\widehat{DCA}$ và $\widehat{BAC},\widehat{DCA}$ ở vị trí so le trong nên AB // CD.

$\widehat{ACB}=\widehat{CAD}$ và $\widehat{ACB},\widehat{CAD}$ ở vị trí so le trong nên AD // BC.

Tứ giác ABCD có AB // CD và AD // BC nên là hình bình hành.

b) • Xét ΔABO và ΔCDO có:

OA = OC (giả thiết); $\widehat{AOB}=\widehat{COD}$ (đối đỉnh); OB = OD (giả thiết)

Do đó ΔABO = ΔCDO (c.g.c)

Suy ra $\widehat{BAO}=\widehat{DCO}$ (cặp góc tương ứng)

Hay $\widehat{BAC}=\widehat{DCA}$.

Chứng minh tương tự ta cũng có: ΔCBO = ΔADO (c.g.c)

Suy ra $\widehat{OCB}=\widehat{OAD}$ (cặp góc tương ứng)

Hay $\widehat{ACB}=\widehat{CAD}$.

• Ta có $\widehat{BAC}=\widehat{DCA}$ và $\widehat{BAC},\widehat{DCA}$ ở vị trí so le trong nên AB // CD.

$\widehat{ACB}=\widehat{CAD}$ và $\widehat{ACB},\widehat{CAD}$ ở vị trí so le trong nên AD // BC.

Tứ giác ABCD có AB // CD và AD // BC nên là hình bình hành.

Giải Toán 8 trang 107 Tập 1

Luyện tập 2 trang 107 Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và $\widehat{OAD}=\widehat{OCB}$. Chứng minh tứ giác ABCD là hình bình hành.

Lời giải:

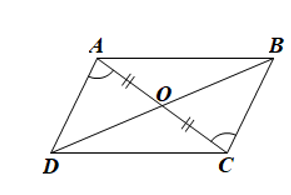
• Xét ΔOAD và ΔOCB có:

$\widehat{OAD}=\widehat{OCB}$ (giả thiết);

OA = OC (giả thiết);

$\widehat{AOD}=\widehat{COB}$ (đối đỉnh)

Do đó ΔOAD = ΔOCB (g.c.g)

Suy ra OD = OB (hai cạnh tương ứng)

• Xét tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường

Do đó ABCD là hình bình hành.

Bài tập

Bài 1 trang 107, 108 Toán 8 Tập 1: Cho tứ giác ABCD có $\widehat{DAB}=\widehat{BCD},\widehat{ABC}=\widehat{CDA}$. Kẻ tia Ax là tia đối của tia AB. Chứng minh:

a) $\widehat{ABC}+\widehat{DAB}=180º$;

b) $\widehat{xAD}=\widehat{ABC}$; AD // BC;

c) Tứ giác ABCD là hình bình hành.

Lời giải:

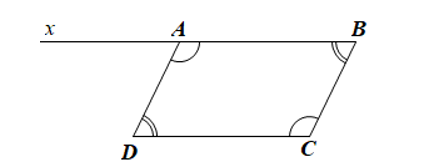
a) Xét tứ giác ABCD có:

$\widehat{DAB}+\widehat{ABC}+\widehat{BCD}+\widehat{CDA}=360°$ (tổng các góc của một tứ giác)

Mà $\widehat{DAB}=\widehat{BCD}$, $\widehat{ABC}=\widehat{CDA}$ (giả thiết)

Nên $\widehat{DAB}+\widehat{ABC}+\widehat{DAB}+\widehat{ABC}=360°$

$2\widehat{ABC}+2\widehat{DAB}=360°$

$2\left(\widehat{ABC}+\widehat{DAB}\right)=360°$

$\widehat{ABC}+\widehat{DAB}=180°$.

Vậy $\widehat{ABC}+\widehat{DAB}=180°$.

b) Ta có $\widehat{xAD}+\widehat{DAB}=180°$ (hai góc kề bù)

Mà $\widehat{ABC}+\widehat{DAB}=180°$ (câu a)

Suy ra $\widehat{xAD}=\widehat{ABC}$

Mà hai góc trên ở vị trí đồng vị nên AD // BC.

c) Xét tứ giác ABCD có: $\widehat{DAB}=\widehat{BCD}$, $\widehat{ABC}=\widehat{CDA}$ (giả thiết)

Do đó tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).

Giải Toán 8 trang 108 Tập 1

Bài 2 trang 108 Toán 8 Tập 1: Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.

Lời giải:

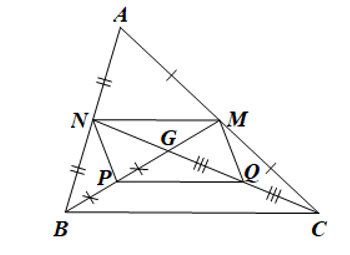
• Xét ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G (giả thiết) nên G là trọng tâm của ΔABC.

Suy ra $GM=\frac{GB}{2}$; $GN=\frac{GC}{2}$ (tính chất trọng tâm của tam giác) (1)

Mà P là trung điểm của GB (giả thiết) nên $GP=PB=\frac{GB}{2}$ (2)

Q là trung điểm của GC (giả thiết) nên $GQ=QC=\frac{GC}{2}$ (3)

Từ (1), (2) và (3) suy ra GM = GP và GN = GQ.

• Xét tứ giác PQMN có: GM = GP và GN = GQ (chứng minh trên)

Do đó tứ giác PQMN có hai đường chéo MP và NQ cắt nhau tại trung điểm G của mỗi đường nên là hình bình hành.

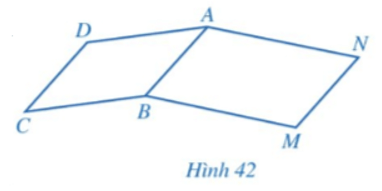
Bài 3 trang 108 Toán 8 Tập 1: Cho hai hình bình hành ABCD và ABMN (Hình 42). Chứng minh:

a) CD = MN;

b) $\widehat{BCD}+\widehat{BMN}=\widehat{DAN}$.

Lời giải:

a) Vì ABCD là hình bình hành (giả thiết) nên AB = CD (tính chất) (1)

Vì ABMN là hình bình hành (giả thiết) nên AB = MN (tính chất) (2)

Từ (1), (2) suy ra CD = MN.

b) Vì ABCD là hình bình hành (giả thiết) nên $\widehat{BCD}=\widehat{DAB}$ (tính chất) (3)

Vì ABMN là hình bình hành (giả thiết) nên $\widehat{BMN}=\widehat{BAN}$ (tính chất) (4)

Mà $\widehat{DAN}=\widehat{DAB}+\widehat{BAN}$ (5)

Từ (3), (4) và (5) suy ra $\widehat{BCD}+\widehat{BMN}=\widehat{DAN}$

Bài 4 trang 108 Toán 8 Tập 1: Để đo khoảng cách giữa hai vị trí A, B ở hai phía của một toà nhà mà không thể trực tiếp đo được, người ta làm như sau: Chọn các vị trí O, C, D sao cho O không thuộc đường thẳng AB; khoảng cách CD là đo được; O là trung điểm của cả AC và BD (Hình 43). Người ta đo được CD = 100 m. Tính độ dài của AB.

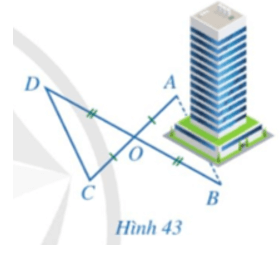
Lời giải:

Xét tứ giác ABCD có: hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Do đó AB = CD = 100 (m).

Bài 5 trang 108 Toán 8 Tập 1: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc C (Hình 44). Bạn Hoa đố bạn Hùng: Không vẽ lại tam giác ABC, làm thế nào tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB?

Bạn Hùng đã làm như sau:

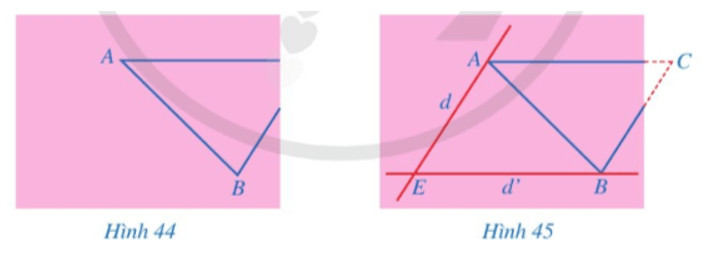
– Qua điểm A kẻ đường thẳng d song song với BC, qua điểm B kẻ đường thẳng d’ song song với AC;

– Gọi E là giao điểm của d và d’;

– Đo độ dài các đoạn thẳng AE, BE và đo góc AEB. Từ đó, tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB (Hình 45).

Em hãy giải thích cách làm của bạn Hùng.

Lời giải:

• Vì d // BC (giả thiết) nên AE // BC;

Vì d’ // AC (giả thiết) nên BE // AC.

• Xét tứ giác ACBE có: AE // BC (chứng minh trên) và BE // AC (chứng minh trên)

Do đó tứ giác ACBE là hình bình hành

Suy ra $\left\{\begin{array}{l}AC=BE\\ BC=AE\\ \widehat{ACB}=\widehat{AEB}\end{array}\right.$ (tính chất hình bình hành)

Bạn Hùng chứng minh được tứ giác ACBE là hình bình hành có các tính chất trên, đo độ dài các đoạn thẳng BE, AE và đo góc AEB. Từ đó, tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB (Hình 45).

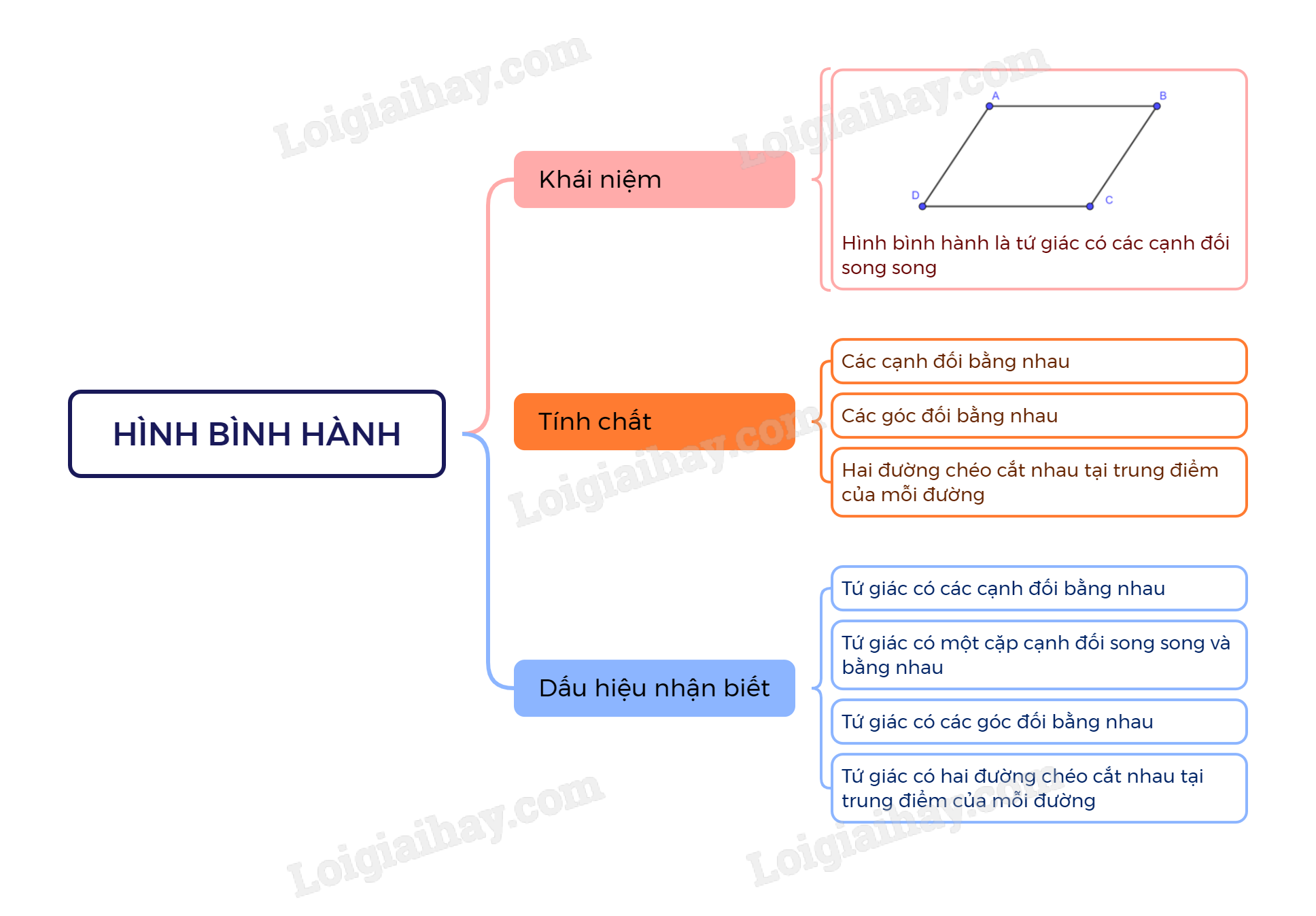
Lý thuyết Hình bình hành

1. Khái niệm

Hình bình hành là tứ giác có các cạnh đối song song.

2. Tính chất

Trong hình bình hành:

- Các cạnh đối bằng nhau;

- Các góc đối bằng nhau;

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết

- Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

- Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

- Tứ giác có các góc đối bằng nhau là một hình bình hành.

- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.

Ví dụ:

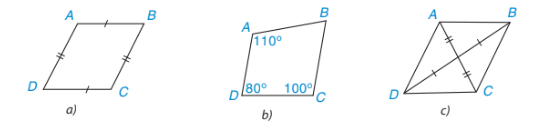
Hình a và c là hình bình hành do:

Hình a có các cặp cạnh đối bằng nhau.

Hình b có các đường chéo cắt nhau tại trung điểm của mỗi đường.

Xem thêm lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5