Toán 8 Bài 3 (Cánh diều): Hàm số bậc nhất y = ax + b (a khác 0)

Giải Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a khác 0)

Bài giải Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a khác 0)

Giải Toán 8 trang 67 Tập 1

Khởi động trang 67 Toán 8 Tập 1: Một doanh nghiệp xuất khẩu gạo thu mua thóc với giá 7 triệu đồng/tấn. Do thóc thu mua được có chất lượng cao nên doanh nghiệp đã thưởng thêm cho nhà sản xuất 6 triệu đồng. Gọi y (triệu đồng) là tổng số tiền mà doanh nghiệp đã trả cho nhà sản xuất để mua x tấn thóc. Viết công thức tính y theo x.

Hàm số cho bằng công thức tính y theo x ở trên gợi nên khái niệm nào trong toán học?

Lời giải:

Sau khi học xong bài này ta sẽ giải quyết bài toán này như sau:

Với y (triệu đồng) là tổng số tiền mà doanh nghiệp đã trả cho nhà sản xuất để mua x tấn thóc thì công thức tính y theo x là: y = 7x + 6.

Hàm số cho bằng công thức tính y theo x là hàm số bậc nhất.

I. Hàm số bậc nhất

Hoạt động 1 trang 67 Toán 8 Tập 1: Trong bài toán ở phần mở đầu, công thức tính y theo x có phải là đa thức bậc nhất của biến x hay không?

Lời giải:

Do y = 7x + 6 nên y là một đa thức bậc nhất của biến x.

Hàm số y = 7x + 6 là hàm số bậc nhất.

Luyện tập 1 trang 67 Toán 8 Tập 1: Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Đối với những hàm số bậc nhất đó, xác định hệ số a của x, hệ số tự do b.

a) y = − 3x + 6.

b) y = − x + 4.

c) $y=\frac{3}{x}+2$.

d) y = 2.

Lời giải:

Các hàm số là hàm số bậc nhất là y = − 3x + 6; y = − x + 4.

• Hàm số y = − 3x + 6 có hệ số a của x là a = − 3 và hệ số tự do b = 6;

• Hàm số y = − x + 4 có hệ số a của x là a = − 1 và hệ số tự do b = 4.

Giải Toán 8 trang 68 Tập 1

Luyện tập 2 trang 68 Toán 8 Tập 1: Cho hàm số y = −2x + 4. Tìm giá trị của y tương ứng với mỗi giá trị của x: x = 0; x = 2; x = 4.

Lời giải:

• Với x = 0 thì y = − 2 . 0 + 4 = 0 + 4 = 4;

• Với x = 2 thì y = − 2 . 2 + 4 = − 4 + 4 = 0;

• Với x = 4 thì y = − 2 . 4 + 4 = − 8 + 4 = − 4.

Vậy với x = 0; x = 2; x = 4 thì giá trị tương ứng của y lần lượt là y = 4; y = 0; y = − 4.

II. Ứng dụng

Giải Toán 8 trang 69 Tập 1

Luyện tập 3 trang 69 Toán 8 Tập 1: Nếu hiện tại nước Anh là mùa đông thì London ở múi giờ + 0, Hà Nội ở múi giờ + 7. Giả sử vào thời điểm mùa đông của nước Anh, giờ London là x (giờ), giờ Hà Nội là y (giờ). Viết công thức biểu thị y theo x. Hỏi y có phải là hàm số bậc nhất của x hay không?

Lời giải:

Với giờ London là x (giờ), giờ Hà Nội là y (giờ) thì công thức biểu thị y theo x là:

y = x + 7.

Vậy y là hàm số bậc nhất của x.

Bài tập

Giải Toán 8 trang 70 Tập 1

Bài 1 trang 70 Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước.

b) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và a khác 0.

c) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và b khác 0.

Lời giải:

Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và a khác 0.

Do đó phát biểu a), c) sai; phát biểu b) đúng.

Bài 2 trang 70 Toán 8 Tập 1: Xác định các hệ số của x, hệ số tự do trong mỗi hàm số bậc nhất sau:

a) y = 6x + 8;

b) y = – x – 5;

c) $y=\frac{x}{3}$.

Lời giải:

a) Hàm số y = 6x + 8 có hệ số của x là 6; hệ số tự do là 8;

b) Hàm số y = – x – 5 có hệ số của x là 1; hệ số tự do là – 5;

c) Ta có $y=\frac{x}{3}=\frac{1}{3}x$ có hệ số của x là $\frac{1}{3}$; hệ số tự do là 0.

Bài 3 trang 70 Toán 8 Tập 1: Cho hàm số bậc nhất f(x) = 3x + 2. Tính $f\left(1\right);f\left(0\right);f(-2);f\left(\frac{1}{2}\right);f\left(-\frac{2}{3}\right).$

Lời giải:

• f(1) = 3 . 1 + 2 = 3 + 2 = 5;

• f(0) = 3 . 0 + 2 = 0 + 2 = 5;

• f(– 2) = 3 . (– 2) + 2 = – 6 + 2 = – 4;

• $f\left(\frac{1}{2}\right)=3.\frac{1}{2}+2=\frac{3}{2}+2=\frac{7}{2}$;

• $f\left(-\frac{2}{3}\right)=3.\left(-\frac{2}{3}\right)+2=-2+2=0$.

Bài 4 trang 70 Toán 8 Tập 1: Hiện tại, bạn Nam đã để dành được 300 000 đồng. Bạn Nam đang có ý định mua một chiếc xe đạp trị giá 2 000 000 đồng. Để thực hiện được điều trên, bạn Nam đã lên kế hoạch mỗi ngày tiết kiệm 5 000 đồng. Gọi m (đồng) là số tiền bạn Nam tiết kiệm được sau t ngày theo kế hoạch.

a) Viết công thức biểu thị m theo t. Hỏi m có phải là hàm số bậc nhất của t hay không?

b) Hỏi sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó?

Lời giải:

a) Mỗi ngày bạn Nam tiết kiệm 5 000 đồng.

Công thức biểu thị m theo t là: m = 5 000t (đồng).

Với mỗi giá trị của t thì ta xác định được giá trị m tương ứng và 5 000 ≠ 0.

Do đó, m là hàm số bậc nhất của t.

b) Số tiền còn lại Nam cần để dành để Nam đủ tiền mua chiếc xe đạp là:

2 000 000 – 300 000 = 1 700 000 (đồng).

Khi đó, m = 1 700 000 (đồng).

Ta có m = 5 000t nên $t=\frac{1700000}{5000}=340$ (ngày).

Vậy sau 340 ngày kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó.

Bài 5 trang 70 Toán 8 Tập 1: Một người đang sử dụng Internet, mỗi phút tốn dung lượng 1 MB. Giả sử gói cước Internet của người đó cho phép sử dụng dung lượng 4 MB.

a) Viết hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng Internet x (giây).

b) Viết hàm số g(x) biểu thị dung lượng cho phép còn lại (MB) sau khi sử dụng Internet được x (giây).

c) Sau khi sử dụng Internet 2 phút thì dung lượng còn lại cho phép còn lại là bao nhiêu Megabyte?

Lời giải:

a) Đổi: 1 phút = 60 giây.

Mỗi phút tốn dung lượng 1 MB.

Mỗi giây tốn $\frac{1}{60}$ MB.

Hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng Internet x (giây) là:

$f\left(x\right)=\frac{1}{60}x$ (MB).

b) Hàm số g(x) biểu thị dung lượng cho phép còn lại (MB) sau khi sử dụng Internet được x (giây) là:

$g\left(x\right)=4-\frac{1}{60}x$ (MB).

c) Cách 1:

Mỗi phút tốn dung lượng 1 MB nên sau khi sử dụng Internet 2 phút thì tiêu tốn 2 MB.

Dung lượng còn lại cho phép còn lại là: 4 – 2 = 2 (MB).

Vậy sau khi sử dụng Internet 2 phút thì dung lượng còn lại cho phép còn lại là 2 Megabyte.

Cách 2:

Đổi 2 phút = 120 giây.

Sau khi sử dụng Internet 2 phút thì dung lượng còn lại cho phép còn lại là:

$g\left(120\right)=4-\frac{1}{60}.120=4-2=2$ (MB).

Vậy sau khi sử dụng Internet 2 phút thì dung lượng còn lại cho phép còn lại là 2 Megabyte.

Bài 6 trang 70 Toán 8 Tập 1: Bạn Dương mang theo 100 000 đồng và đạp xe đi nhà sách để mua vở. Biết giá mỗi quyển vở là 7 000 đồng, phí gửi xe đạp là 3 000 đồng.

a) Viết công thức biểu thị tổng số tiền y (đồng) bạn Dương cần trả cho việc gửi xe đạp và mua x quyển vở. Hỏi y có phải là hàm số bậc nhất của x hay không?

b) Tính số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở.

c) Với số tiền trên, bạn Dương có thể mua 15 quyển vở hay không? Vì sao?

Lời giải:

a) Giá tiền x quyển vở là: 7 000x (đồng).

Công thức biểu thị tổng số tiền y (đồng) số tiền bạn Dương cần trả cho việc gửi xe đạp và mua x quyển vở là: y = 7 000x + 3 000 (đồng).

b) Số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở là:

7 000 . 12 + 3 000 = 87 000 (đồng).

c) Số tiền cần phải trả khi gửi xe và mua 15 quyển vở là:

7 000 . 15 + 3 000 = 108 000 (đồng).

Vì 108 000 > 100 000 nên với số tiền trên, bạn Dương không thể mua 15 quyển vở.

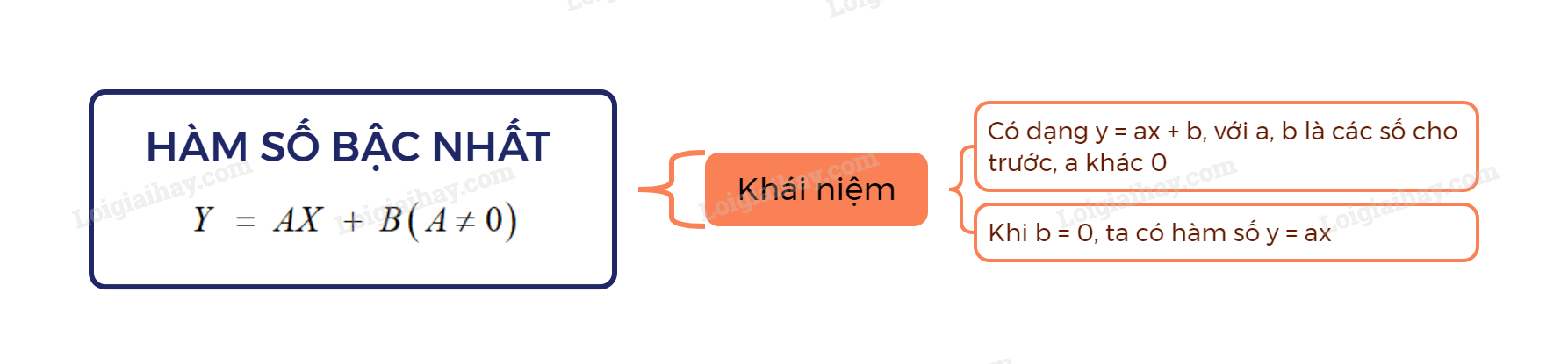
Lý thuyết Hàm số bậc nhất y = ax + b (a ≠ 0)

Khái niệm

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là các số cho trước và a khác 0.

Chú ý: Khi b = 0, ta có hàm số y = ax.

Ví dụ: y = 2x – 3 là hàm số bậc nhất với a = 2 và b = -3

y = x + 4 là hàm số bậc nhất với a = 1, b = 4

Xem thêm lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0)

Bài tập cuối chương 3

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều