Toán 8 Bài 1 (Cánh diều): Định lí Thalès trong tam giác

Giải Toán 8 Bài 1: Định lí Thalès trong tam giác

Giải Toán 8 trang 52 Tập 2

Khởi động trang 52 Toán 8 Tập 2: Bác Dư muốn cắt một thanh sắt (Hình 1) thành 5 phần bằng nhau nhưng bác lại không có thước để đo.

Bác Dư có thể thực hiện điều đó bằng cách nào?

Lời giải:

Sau bài học này, chúng ta có thể giải quyết câu hỏi trên như sau:

Bác Dư có thể làm như sau:

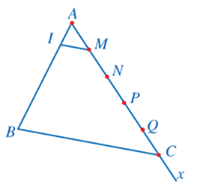
– Đặt thanh sắt trên mặt phẳng sân và coi thanh sắt như đoạn thẳng AB.

– Vẽ tia Ax và lấy một đoạn dây không dãn nào đó rồi đặt liên tiếp trên tia Ax, bắt đầu từ điểm A, năm đoạn thẳng AM, MN, NP, PQ, QC có độ dài đều bằng độ dài đoạn dây.

– Trong tam giác ABC, kẻ đường thẳng qua M song song với cạnh BC, cắt cạnh AB tại I.

Theo định lí Thalès, ta có $\frac{\mathrm{AI}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AC}}=\frac{1}{5}.$ Do đó $\mathrm{AI}=\frac{1}{5}\mathrm{AB}.$

Dựa theo đoạn mẫu AI, bác Dư có thể cắt một thanh sắt thành năm phần bằng nhau.

I. Đoạn thẳng tỷ lệ

Hoạt động 1 trang 52 Toán 8 Tập 2: Cho hai đoạn thẳng AB = 2 cm, CD = 3 cm và hai đoạn thẳng MN = 4 cm, PQ = 6 cm. So sánh hai tỉ số $\frac{\mathrm{AB}}{\mathrm{CD}},\frac{\mathrm{MN}}{\mathrm{PQ}}.$

Lời giải:

Ta có: $\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{2}{3}$ và $\frac{\mathrm{MN}}{\mathrm{PQ}}=\frac{4}{6}=\frac{2}{3}.$

Vậy $\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{\mathrm{MN}}{\mathrm{PQ}}=\frac{2}{3}.$

II. Định lí Thalès trong tam giác

Giải Toán 8 trang 53 Tập 2

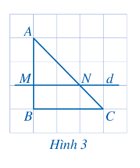
Hoạt động 2 trang 53 Toán 8 Tập 2: Quan sát Hình 3 và cho biết:

a) Đường thẳng d có song song với BC hay không;

b) Bằng cách đếm số ô vuông, dự đoán xem các tỉ số $\frac{\mathrm{AM}}{\mathrm{MB}},\frac{\mathrm{AN}}{\mathrm{NC}}$ có bằng nhau hay không.

Lời giải:

a) Đường thẳng dvà BC nằm trên hai dòng kẻ nên đường thẳng d song song với BC;

b) Ta có $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{2}{1}=2$ và $\frac{\mathrm{AN}}{\mathrm{NC}}=\frac{2}{1}=2.$

Vậy $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}=2.$

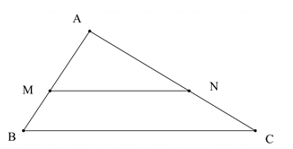
Luyện tập 1 trang 53 Toán 8 Tập 2: Trong Hình 4, chứng tỏ rằng nếu MN // BCthì $\frac{\mathrm{MB}}{\mathrm{AB}}=\frac{\mathrm{NC}}{\mathrm{AC}}.$

Lời giải:

Do MN // BC nên theo định lí Thalès, ta có: $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}.$

Suy ra $\frac{\mathrm{AM}}{\mathrm{AN}}=\frac{\mathrm{MB}}{\mathrm{NC}}$ (tính chất tỉ lệ thức)

Do đó $\frac{\mathrm{AM}}{\mathrm{AN}}=\frac{\mathrm{MB}}{\mathrm{NC}}=\frac{\mathrm{AM}+\mathrm{MB}}{\mathrm{AN}+\mathrm{NC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ (tính chất dãy tỉ số bằng nhau)

Hay $\frac{\mathrm{MB}}{\mathrm{NC}}=\frac{\mathrm{AB}}{\mathrm{AC}},$ nên $\frac{\mathrm{MB}}{\mathrm{AB}}=\frac{\mathrm{NC}}{\mathrm{AC}}.$

Luyện tập 2 trang 53 Toán 8 Tập 2: Cho tam giác ABC có G là trọng tâm. Đường thẳng qua G song song với BC lần lượt cắt cạnh AB, AC tại M, N. Chứng minh $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{2}{3}.$

Lời giải:

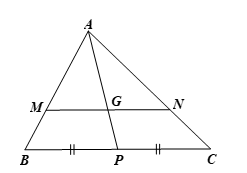
Gọi P là trung điểm của BC.

Xét ∆ABP với MG // BN (do G ∈ MN, P ∈ BC), ta có:

$\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AG}}{\mathrm{GP}}$ (định lí Thalès)

Suy ra $\frac{\mathrm{AM}}{\mathrm{AG}}=\frac{\mathrm{MB}}{\mathrm{GP}}$ (tính chất tỉ lệ thức)

Do đó $\frac{\mathrm{AM}}{\mathrm{AG}}=\frac{\mathrm{MB}}{\mathrm{GP}}=\frac{\mathrm{AM}+\mathrm{MB}}{\mathrm{AG}+\mathrm{GP}}=\frac{\mathrm{AB}}{\mathrm{AP}}$ (tính chất dãy tỉ số bằng nhau)

Hay $\frac{\mathrm{AM}}{\mathrm{AG}}=\frac{\mathrm{AB}}{\mathrm{AP}},$ nên $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AG}}{\mathrm{AP}}.$

Mà G là trọng tâm ∆ABC nên $\frac{\mathrm{AG}}{\mathrm{AP}}=\frac{2}{3}$ (tính chất trọng tâm của một tam giác)

Do đó, $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AG}}{\mathrm{AP}}=\frac{2}{3}$ (1)

Tương tự, xét ∆ABC với MN // BC ta cũng có $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$ (2)

Từ (1) và (2), suy ra $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{2}{3}.$

Giải Toán 8 trang 54 Tập 2

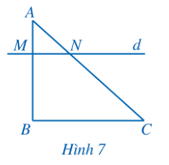
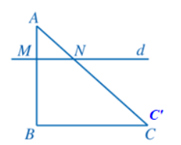
Hoạt động 3 trang 54 Toán 8 Tập 2: Trong Hình 7, cho AM = 1, MB = 2, AN = 1,5, NC = 3.

a) So sánh các tỉ số $\frac{\mathrm{AM}}{\mathrm{MB}};\frac{\mathrm{AN}}{\mathrm{NC}}.$

b) Đường thẳng d (đi qua M, N ) có song song với BC hay không?

Lời giải:

a) Ta có $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{1}{2}$ và $\frac{AN}{NC}=\frac{1,5}{3}=\frac{1}{2}.$

Vậy $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$ (cùng bằng $\frac{1}{2}$)

b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.

Xét ∆ABC’ với MN // BC’, ta có:

$\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{{\mathrm{NC}}^{\text{'}}}$ (định lí Thalès).

Mà theo câu a, $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$ nên ta có $\frac{\mathrm{AN}}{\mathrm{NC}}=\frac{\mathrm{AN}}{{\mathrm{NC}}^{\text{'}}}$

Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.

Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.

Vậy đường thẳng d (đi qua M, N) song song với BC.

Giải Toán 8 trang 55 Tập 2

Luyện tập 3 trang 55 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.

Lời giải:

Ta có: $\frac{\mathrm{CN}}{\mathrm{CB}}=\frac{1,25}{5}=\frac{1}{4}$ và $\frac{\mathrm{CM}}{\mathrm{CA}}=\frac{1}{4}.$

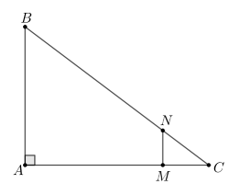
Do đó, $\frac{\mathrm{CN}}{\mathrm{CB}}=\frac{\mathrm{CM}}{\mathrm{CA}}\left(=\frac{1}{4}\right).$

Trong ∆ABC, có $\frac{\mathrm{CN}}{\mathrm{CB}}=\frac{\mathrm{CM}}{\mathrm{CA}}$

Suy ra MN // AB (định lí Thalès đảo)

Mà AB ⊥ AC (do tam giác ABC vuông tại A) nên MN ⊥ AC tại M.

Xét ∆MNC vuông tại M có:CN² = CM²+ MN²(định lí Pythagore)

Suy ra, $\mathrm{MN}=\sqrt{{\mathrm{CN}}^2-{\mathrm{CM}}^2}=\sqrt{1,{25}^2-1^2}=0,75\left(\text{cm}\right).$

Bài tập

Giải Toán 8 trang 57 Tập 2

Bài 1 trang 57 Toán 8 Tập 2: Cho tam giác ABC có AB = 4,5 cm; AC = 6 cm. Các điểm M, N lần lượt thuộc các cạnh AB, AC thoả mãn AM = 3 cm và MN // BC. Tính độ dài đoạn thẳng AN.

Lời giải:

Xét ∆ABC với MN // BC, ta có:

$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$ (Hệ quả của định lí Thalès)

Suy ra $\frac{3}{4,5}=\frac{\mathrm{AN}}{6}$

Do đó $\mathrm{AN}=\frac{3\cdot 6}{4,5}=4\left(\text{cm}\right).$

Bài 2 trang 57 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có AB = 4 cm, CD = 6 cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.

a) Chứng minh $\frac{\mathrm{AM}}{\mathrm{MD}}=\frac{\mathrm{BN}}{\mathrm{NC}};$

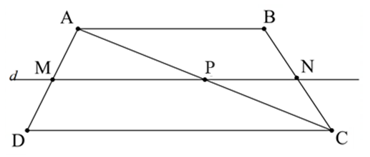
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.

Lời giải:

a) Do d // CD, mà M, N, P ∈ d nên MP // CD, PN // CD, MN // CD

Do ABCD là hình thang nên AB // CD, do đó PN // AB

Xét ∆ADC với MP // CD, ta có $\frac{\mathrm{AM}}{\mathrm{MD}}=\frac{\mathrm{AP}}{\mathrm{PC}}$ (định lí Thalès) (1)

Xét ∆ABC với PN // AB, ta có $\frac{\mathrm{AP}}{\mathrm{PC}}=\frac{\mathrm{BN}}{\mathrm{NC}}$ (định lí Thalès) (2)

Từ (1) và (2) suy ra $\frac{\mathrm{AM}}{\mathrm{MD}}=\frac{\mathrm{BN}}{\mathrm{NC}}\left(=\frac{\mathrm{AP}}{\mathrm{PC}}\right).$

b) ⦁Do MD = 2MA nên $\frac{\mathrm{MA}}{\mathrm{MD}}=\frac{1}{2}.$

Suy ra $\frac{\mathrm{MA}}{\mathrm{MD}+\mathrm{MA}}=\frac{1}{2+1}$ hay $\frac{\mathrm{AM}}{\mathrm{AD}}=\frac{1}{3}.$

⦁Xét ∆ADC với MP // CD, ta có $\frac{\mathrm{AM}}{\mathrm{AD}}=\frac{\mathrm{AP}}{\mathrm{AC}}=\frac{\mathrm{MP}}{\mathrm{DC}}$ (hệ quả định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{DC}}=\frac{\mathrm{AP}}{\mathrm{AC}}=\frac{\mathrm{AM}}{\mathrm{AD}}=\frac{1}{3}.$ Do đó $\mathrm{MP}=\frac{\mathrm{DC}}{3}=\frac{6}{3}=2\left(\text{cm}\right).$

⦁ Tương tự, xét ∆ABC vớiPN // AB, ta có $\frac{\mathrm{CN}}{\mathrm{BC}}=\frac{\mathrm{CP}}{\mathrm{AC}}=\frac{\mathrm{PN}}{\mathrm{AB}}$ (hệ quả định lí Thalès)

Mà $\frac{\mathrm{AP}}{\mathrm{AC}}=\frac{1}{3}$ hay $\frac{\mathrm{AC}-\mathrm{CP}}{\mathrm{AC}}=\frac{1}{3},$ do đó $1-\frac{\mathrm{CP}}{\mathrm{AC}}=\frac{1}{3}$ nên $\frac{\mathrm{CP}}{\mathrm{AC}}=1-\frac{1}{3}=\frac{2}{3}.$

Khi đó $\frac{\mathrm{PN}}{\mathrm{AB}}=\frac{\mathrm{CP}}{\mathrm{AC}}=\frac{2}{3}$ nên $\mathrm{PN}=\frac{2}{3}\mathrm{AB}=\frac{2}{3}\cdot 4=\frac{8}{3}\left(\text{cm}\right).$

Ta có: $\mathrm{MN}=\mathrm{MP}+\mathrm{PN}=2+\frac{8}{3}=\frac{14}{3}\left(\text{cm}\right).$

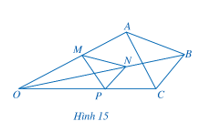
Bài 3 trang 57 Toán 8 Tập 2: Trong Hình 15, cho MN // AB, NP // BC. Chứng minh MP // AC.

Lời giải:

Xét ∆OAB với MN // AB, ta có $\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{ON}}{\mathrm{OB}}$ (hệ quả định lí Thalès)

Xét ∆OBC với PN // BC, ta có $\frac{\mathrm{OP}}{\mathrm{OC}}=\frac{\mathrm{ON}}{\mathrm{OB}}$ (hệ quả định lí Thalès)

Do đó, $\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{OP}}{\mathrm{OC}}$

Trong ∆OAC có: $\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{OP}}{\mathrm{OC}}$ nên MP // AC (định lí Thalès đảo).

Bài 4 trang 57 Toán 8 Tập 2: Trong Hình 16, độ dài đoạn thẳng A’C’ mô tả chiều cao của một cái cây, đoạn thẳng AC mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm A’, A, B). Giả sử AC = 2m, AB = 1,5m, A’B = 4,5 m. Tính chiều cao của cây.

Lời giải:

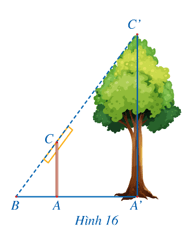
Ta có: AC ⊥ A’B, A’C’ ⊥ A’B nên AC // A’C’

Xét ∆A’BC’ với AC // A’C’, ta có:$\frac{\mathrm{AC}}{A^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{BA}}{{\mathrm{BA}}^{\text{'}}}$ (hệ quả định lí Thalès)

Suy ra $\frac{\mathrm{AC}}{A^{\text{'}}{C}^{\text{'}}}=\frac{1,5}{4,5}=\frac{1}{3}$

Suy ra A’C’ = 3AC = 3.2 = 6 (m).

Vậy cây cao 6m.

Bài 5 trang 57 Toán 8 Tập 2: Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không dùng thước để đo.

Lời giải:

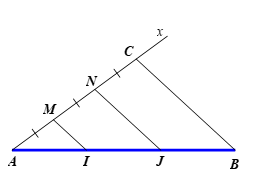
– Vẽ tia Ax và lấy một điểm M trên tia Ax.

– Dùng compa vẽ cung tròn tâm M, bán kính MA, cắt tia Ax tại N (khác A), ta được MN = MA.

Tương tự như vậy, khi đó ta lấy liên tiếp trên tia Ax, bắt đầu từ điểm A, ba đoạn thẳng AM, MN, NC có độ dài bằng nhau.

– Trong tam giác ABC, kẻ đường thẳng qua M song song với cạnh BC, cắt cạnh AB tại I.

Theo định lí Thalès, ta có $\frac{\mathrm{AI}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AC}}=\frac{1}{3}.$ Do đó $\mathrm{AI}=\frac{1}{3}\mathrm{AB}.$

Dựa theo đoạn mẫu AI, ta có thể chia đoạn thẳng AB thành ba phần bằng nhau.

Lý thuyết Định lí Thalès trong tam giác

1. Đoạn thẳng tỉ lệ

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng MN và PQ nếu có tỉ lệ thức: $\frac{AB}{CD}=\frac{MN}{PQ}$

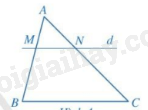
2. Định lí Thalès

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

$\begin{array}{l}\mathrm{\Delta }ABC,MN//BC(M\in AB,N\in AC)\\ \Rightarrow \frac{AM}{AB}=\frac{AN}{AC};\frac{AM}{MB}=\frac{AN}{NC};\frac{BM}{AB}=\frac{NC}{AC}\end{array}$
3. Định lí Thalès đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

$\mathrm{\Delta }ABC,M\in AB,N\in AC,\frac{AM}{MB}=\frac{AN}{NC}\Rightarrow MN//BC$

4. Hệ quả của định lí Thalès

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

$\begin{array}{l}\mathrm{\Delta }ABC,MN//BC(M\in AB,N\in AC)\\ \Rightarrow \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\end{array}$

Chú ý. Hệ quả vẫn đúng cho trường hợp đường thẳng d song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

Sơ đồ tư duy Định lí Thalès trong tam giác

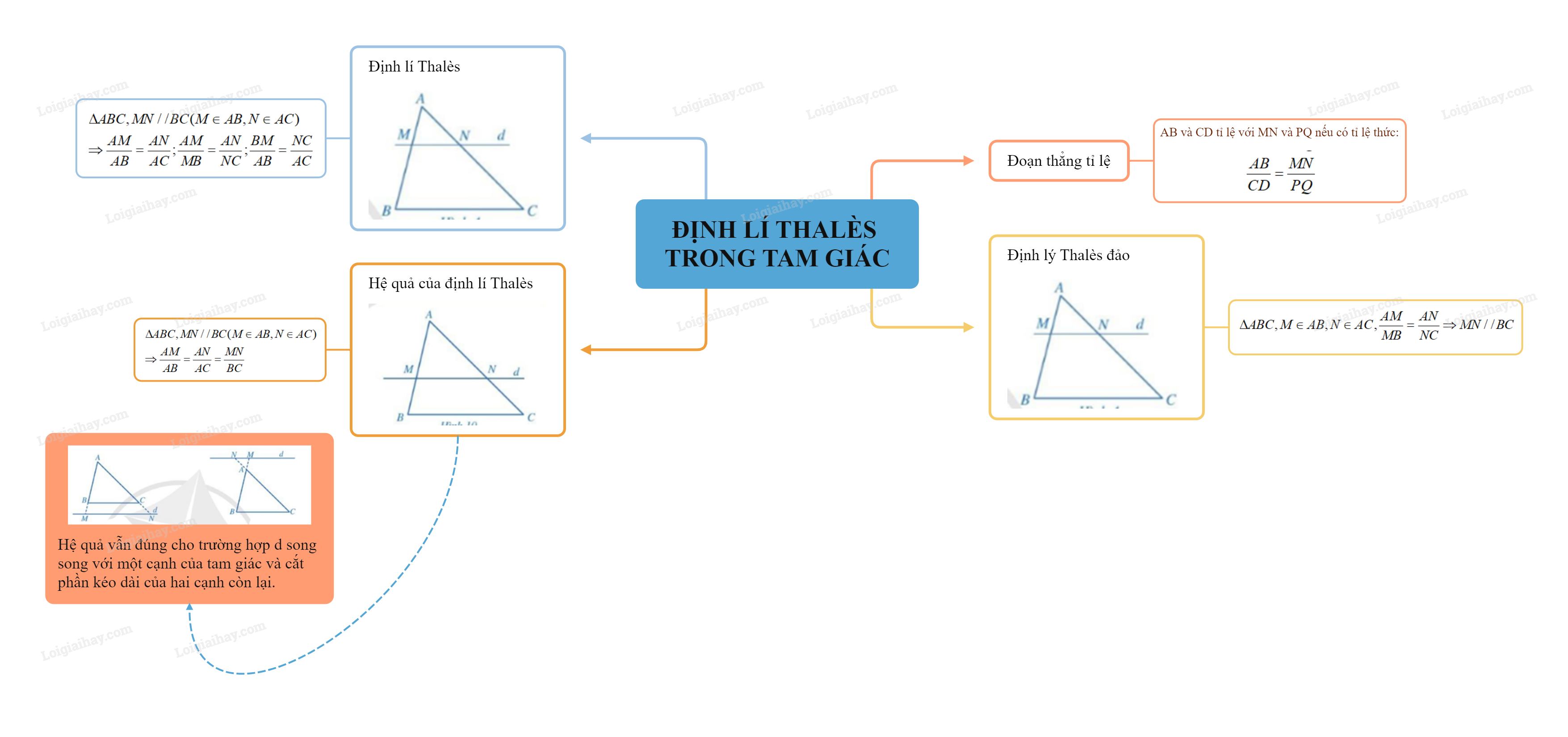
Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Ứng dụng của định lí Thalès trong tam giác

Bài 3: Đường trung bình của tam giác

Bài 4: Tính chất đường phân giác của tam giác

Bài 5: Tam giác đồng dạng

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác