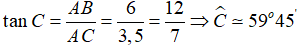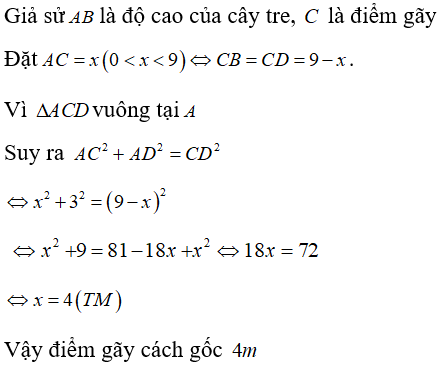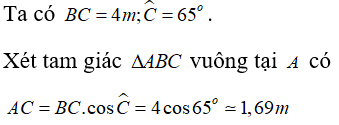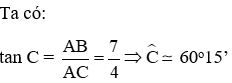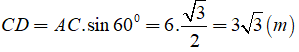50 Bài tập Ứng dụng thực tế các tỉ số lượng giác của góc nhọn Toán 9 mới nhất
Với 50 Bài tập Ứng dụng thực tế các tỉ số lượng giác của góc nhọn Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Ứng dụng thực tế các tỉ số lượng giác của góc nhọn - Toán 9
I. Bài tập trắc nghiệm
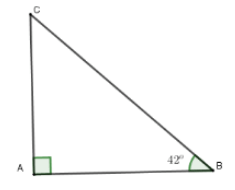
Câu 1: Một cột đèn có bóng trên mặt đất dài 7,5 m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 42°. Tính chiều cao của cột đèn (làm tròn đến chữ số thập phân thứ ba)
A. 6,753 m
B. 6,75 m
C. 6,751 m
D. 6,755 m
Chọn đáp án A
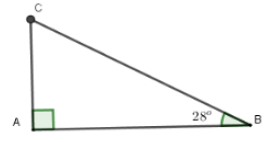
Câu 2: Một cầu trượt trong công viên có độ dốc là 28° và có độ cao là 2,1 m. Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai)
A. 3,95 m
B. 3,8 m
C. 4,5 m
D. 4,47 m
Chọn đáp án D
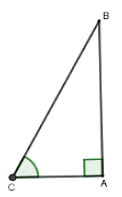
Câu 3: Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5m . Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất
A. 58°45'
B. 59°50'
C. 59°45'
D. 58°4'
Chọn đáp án C
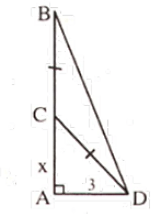
Câu 4: Một cây tre cao 9m bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc 3m . Hỏi điểm gãy cách gốc bao nhiêu?
A. 6m
B. 5m
C. 4m
D. 3m
Chọn đáp án C
Câu 5: Nhà bạn Minh có một chiếc thang dài 4m . Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn ” là 65° (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
A. 1,76 m
B. 1,71 m
C. 1,68 m
D. 1,69 m
Chọn đáp án D
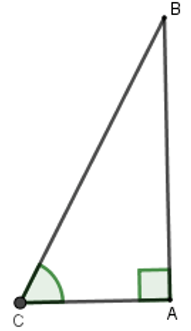
Câu 6: Một cột đèn điện AB cao 7m có bóng in trên mặt đất là AC dài 4m. Hãy tính góc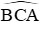 
(làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.
A. 59o45’
B. 62o
C. 61o15’
D. 60o15’
Đáp án cần chọn là: D
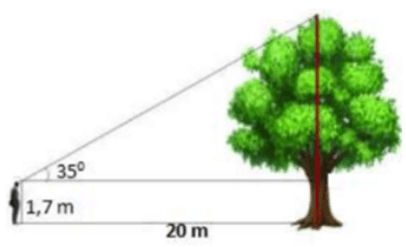
Câu 7: Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
A. 14,3m
B. 15,7m
C. 16,8m
D. 17,2m
Chiều cao của cây là: h = 1,7 + 20. tan35o ≈ 15,7m
Đáp án cần chọn là: B
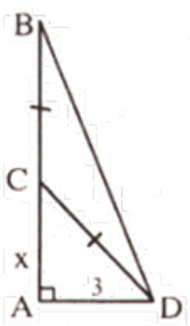
Câu 8: Một cây tre cao 9m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).
A. 6m
B. 5m
C. 4m
D. 3m
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) ⇔ CB = CD = 9 – x. Vì ∆ACD vuông tại A
Suy ra AC2 + AD2 = CD2
⇔ x2 + 32 = (9 – x)2 ⇔ x = 4 (TM)
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C
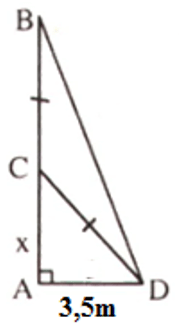
Câu 9: Một cây tre cao 8m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3,5m. Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).
A. 3,32m
B. 3,23m
C. 4m
D. 3m
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x ⇔ CB = CD = 8 – x.
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B
Câu 10: Nhà bạn Minh có một chiếc thang dài 4m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là 65o (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
A. 1,76m
B. 1,71m
C. 1,68m
D. 1,69m
Lời giải:
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
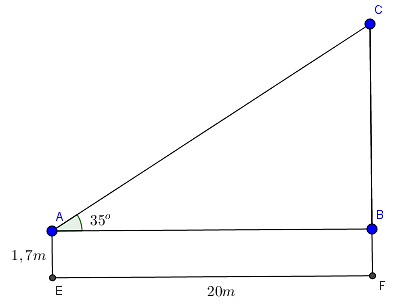
Câu 1: Tính chiều cao của một cây xanh biết rằng một người là 1,7m đứng nhìn lên đỉnh cây thì hướng nhìn tạo với mặt đất một góc 35° và khoảng cách từ người đó đến cây là 20m.
Lời giải:
Ta xem đề bài được biểu diễn như hình vẽ trên với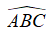 
= 90°
Khi đó chiều cao của cây xanh cần tính là:
CF = BF + BC = AE + AB.tan35° = 1,7 + 20.tan35° ≈ 15,7 (m)
Vậy chiều cao của cây xanh cần tính là ≃ 15,7 (m)
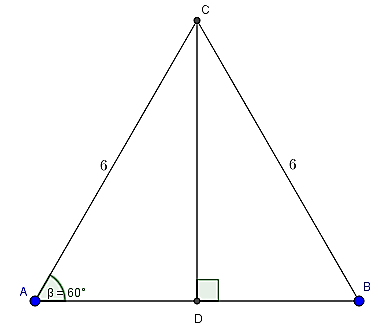
Câu 2: Một chiếc thang gấp đôi dài 6m được người ta sử dụng để leo lên một mái nhà. Biết rằng lúc leo lên mỗi chân thanh tạo với mặt đất một góc 60° . Tính chiều cao của căn nhà đó.
Lời giải:
Xem đề bài như hình vẽ trên
Khi đó tam giác ABC đều và 
Vậy chiều cao của căn nhà đó là 3√3 (m)
III. Bài tập vận dụng
Câu 1: Ở một cái thang đơn dài có ghi “để dảm bảo an toàn cần đặt thang sao cho tạo với mặt đất một góc α thì phải thỏa mãn 60° < α < 75° . Vậy phải đặt thang cách vật thang dựa khoảng bao nhiêu để đảm bảo an toàn?
Câu 2: Cho tam giác ABC vuông tại B có BC = 20 m,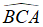 
= 50° . Một đường thẳng song song với BC cắt AB, AC lần lượt tại D, E. Biết BD = 5 m . Tính độ dài AE là?
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Ôn tập chương 1 hình học
Bài tập Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Bài tập Đường kính và dây của đường tròn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9