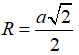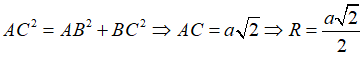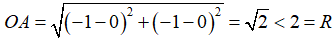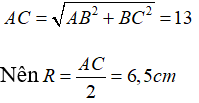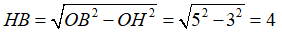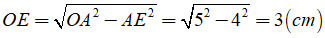50 Bài tập Ôn tập chương 2 Hình học Toán 9 mới nhất
Với 50 Bài tập Ôn tập chương 2 Hình học Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Ôn tập chương 2 Hình học - Toán 9
I. Bài tập trắc nghiệm
Câu 1: Số tâm đối xứng của đường tròn là
A. 1
B. 2
C. 3
D. 4
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn
Chọn đáp án A
Câu 2: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
A. Đường tròn không có trục đối xứng
B. Đường tròn có duy nhất một trục đối xứng là đường kính
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
D. Đường tròn có vô số trục đối xứng là đường kính
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Chọn đáp án D
Câu 3: Tâm của đường tròn ngoại tiếp tam giác là
A. Giao của ba đường phân giác
B. Giao của ba đường trung trực
C. Giao của ba đường cao
D. Giao của ba đường trung tuyến
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó
Chọn đáp án B
Câu 4: Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn
B. Điểm M nằm trên đường tròn
C.Điểm M nằm trong đường tròn
D. Điểm M không thuộc đường tròn
Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:
Chọn đáp án B
Câu 5: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a
A. Tâm là giao điểm A và bán kính R = a√2
B. Tâm là giao điểm hai đường chéo và bán kính R = a√2
C. Tâm là giao điểm hai đường chéo và bán kính
D. Tâm là điểm B và bán kính là
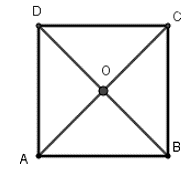
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Chọn đáp án C
Câu 6: Tâm của đường tròn ngoại tiếp tam giác vuông là
A. Trung điểm cạnh huyền
B. Trung điểm cạnh góc vuông lớn hơn
C. Giao ba đường cao
D. Giao ba đường trung tuyến
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp
Chọn đáp án A
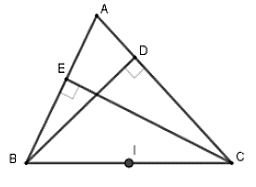
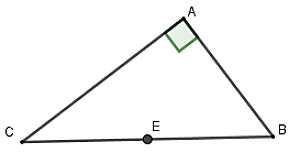
Câu 7: Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó
A. Tâm là trọng tâm tam giác ABC và bán kính R = 2/3 AI với I là trung điểm của
B. Tâm là trung điểm AB và bán kính R = AB/2
C.Tâm là giao điểm của BD và EC, bán kính là R = AB/2
D. Tâm là trung điểm BC và bán kính là R = BC/2
Chọn đáp án D
Câu 8: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A(-1; -1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2
A. Điểm A nằm ngoài đường tròn
B. Điểm A nằm trên đường tròn
C. Điểm A nằm trong đường tròn
D. Không kết luận được
Ta có:
Nên A nằm trong đường tròn tâm O bán kính R = 2
Chọn đáp án C
Câu 9: Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
A. R = 25
B. R = 25/2
C. R = 15
D. R = 20
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính là R = BC/2
Theo định lý Pytago ta có 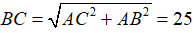
Chọn đáp án B
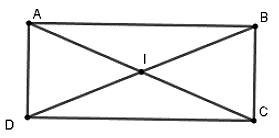
Câu 10: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
A. R = 7,5cm
B. R = 13cm
C. R = 6cm
D. R = 6,5cm
Gọi I là giao hai đường chéo, ta có IA = IB = IC = ID (vì BD = AC và I là trung điểm mỗi đường)
Nếu bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = AC/2
Theo định lý Pytago trong tam giác vuông ABC
Ta có:
Vậy bán kính cần tìm là R = 6,5cm
Chọn đáp án D
Câu 11: Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
A. AB > CD
B. AB = CD
C. AB < CD
D. AB ≤ CD
Trong các dây của đường tròn, dây lớn nhất là đường kính
Chọn đáp án A.
Câu 12: Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng
A. AB > CD
B. AB = CD
C. AB < CD
D. AB // CD
Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau
Chọn đáp án B.
Câu 13: “Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp
A. nhỏ hơn
B. bằng
C. song song
D. vuông góc
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
Chọn đáp án D.
Câu 14: Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
A. Dây nào lớn hơn thì dây đó xa tâm hơn
B. Dây nào nhỏ hơn thì đây đó xa tâm hơn
C. Dây nào gần tâm hơn thì dây đó lớn hơn
D. Hai dây bằng nhau thì cách đều tâm
Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm
- Trong hai dây của đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn
+ Dây nào gần tâm hơn thì dây đó lớn hơn
Nên phương án B, C, D đúng
Chọn đáp án A.
Câu 15: Cho đường tròn (O) có bán kính R = 5 cm. Khoảng cách từ tâm đến dây AB là 3 cm. Tính độ dài dây AB
A. AB = 6 cm
B. AB = 8 cm
C. AB = 10 cm
D. AB = 12 cm
Kẻ OH ⊥ AB tại H suy ra H là trung điểm của AB
Xét tam giác OHB vuông tại H có OH = 3; OB = 5 . Theo định lý Pytago ta có:
Mà H là trung điểm của AB nên AB = 2HB = 8 cm
Vậy AB = 8 cm
Chọn đáp án B.
II. Bài tập tự luận có lời giải
Câu 1: Cho đường tròn tâm O bán kính là 5, dây AB = 8
a) Tính khoảng cách từ O đến AB
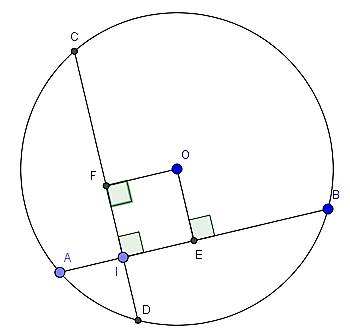
b) Gọi I là điểm thuộc dây AB sao cho AI = 1 , kẻ dây CD đi qua I vuông góc với AB. Chứng minh rằng AB = CD
Lời giải:
a) Gọi E là hình chiếu của O lên AB
Khoảng cách từ O đến AB chính là độ dài đoạn OE
Ta có:
b) Gọi F là hình chiếu của O lên CD
Khi đó khoảng cách của O đến CD chính là OF
Tứ giác OFIE có ba góc vuông nên là hình chữ nhật
Do đó: OF = EI = AE - AI = 4 - 1 = 3
Suy ra OE = OF theo định lí 1 nên AB = CD
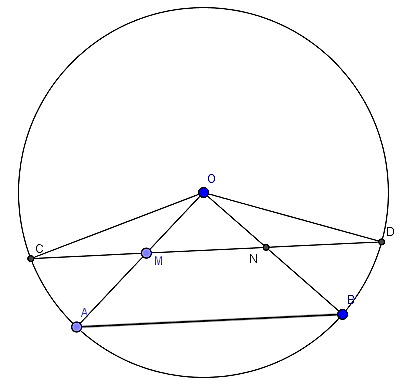
Câu 2: Cho đường tròn (O; R) . Vẽ hai đường tròn bán kính OA, OB. Trên bán kính OA, OB lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua MN (M giữa C và N)
a) Chứng minh: CM = DN
b) Giả sử 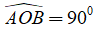
Lời giải:
III. Bài tập vận dụng
Câu 1: Cho hình thang vuông ABCD có A^=B^= 90°; BC = 2AD = 2a. Gọi H là hình chiếu vuông góc của B lên AC , M là trung điểm của HC . Tìm tâm và bán kính đường tròn ngoại tiếp tam giác BDM
Câu 2: Cho hình thang vuông ABCD (A^=B^= 90°) có O là trung điểm của AB và góc 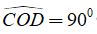
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Hệ hai phương trình bậc nhất hai ẩn
Bài tập Giải hệ phương trình bằng phương pháp thế
Bài tập Giải hệ phương trình bằng phương pháp cộng đại số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9