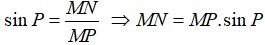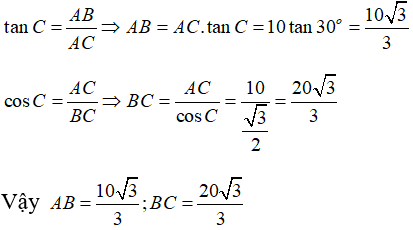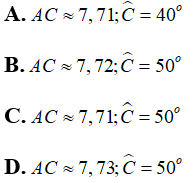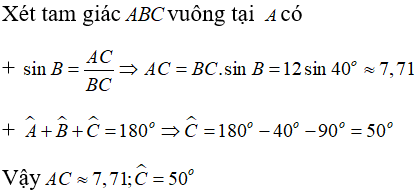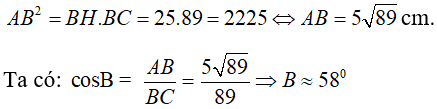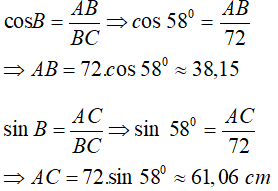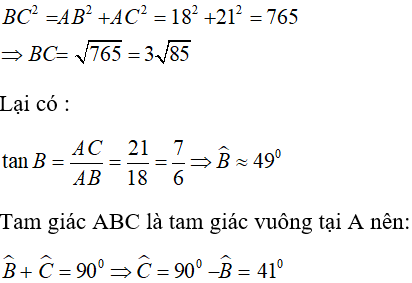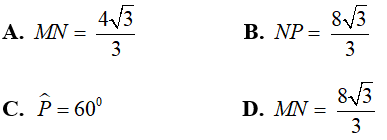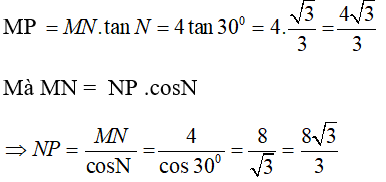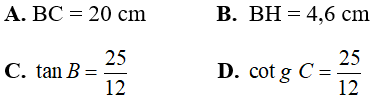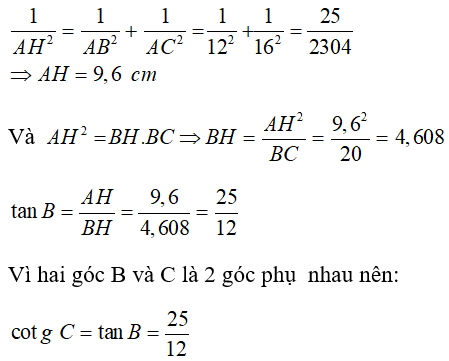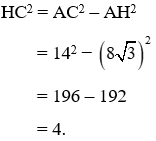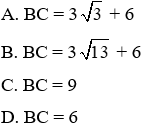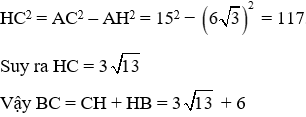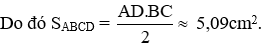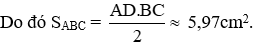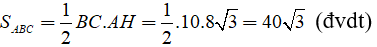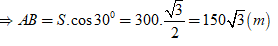50 Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 mới nhất
Với 50 Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông - Toán 9
I. Bài tập trắc nghiệm
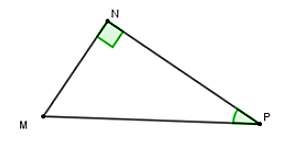
Câu 1: Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?
A. MN = MP.sinP
B. MN = MP.cosP
C. MN = MP.tanP
D. MN = MP.cotP
Ta có: 
Chọn đáp án A
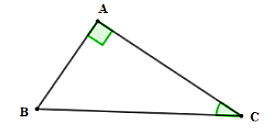
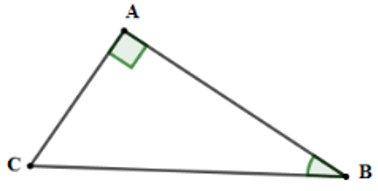
Câu 2: Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?
A. b = a.sinB = a.cosC
B. a = c.tanB = c.cotC
C. a2 = b2 + c2
D. c = a.sinC = a.cosB
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:
+ Theo định lý Pytago ta có a2 = b2 + c2 nên C đúng
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
b = asinB = acosC; c = asinC = acosB; b = ctanB = ccotC; c = btanC = bcotB
Nên A, D đúng
Chọn đáp án B
Câu 3: Cho tam giác ABC vuông tại A có AC = 10 cm, C^= 30°. Tính
Xét tam giác ABC vuông tại A có
Chọn đáp án D
Câu 4: Cho tam giác ABC vuông tại A có BC = 12 cm, B^= 40°. Tính (làm tròn đến chữ số thập phân thứ 2)
Chọn đáp án C
Câu 5: Cho tam giác ABC vuông tại A có BC = 15 cm, AB = 12 cm. Tính AC, B
Chọn đáp án B
Câu 6: Tam giác ABC vuông tại A ; đường cao AH; biết HB = 25cm; HC = 64 cm. Tính góc B
A. 42°
B. 32°
C. 51°
D. 58°
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Chọn đáp án C.
Câu 7: Cho tam giác ABC vuông tại A có BC = 72 cm và góc B = 58° . Tính AB và AC ?
A. 38,15 và 61,06
B. 36,06 và 62,01
C. 37,09 và 60,19
D. 39,01 và 62,93
Ta có:
Chọn đáp án A.
Câu 8: Cho tam giác ABC vuông tại A biết AC = 21 cm và AB = 18 cm. Tìm khẳng định sai ?
Áp dụng định lí pytago ta có:
Chọn đáp án C.
Câu 9: Cho tam giác MNP vuông tại M có MN = 4 và B^= 30° . Tìm khẳng định sai trong các khẳng định sau?
Áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có:
Chọn đáp án D.
Câu 10: Cho tam giác ABC vuông tại A có đường cao AH và AB = 12 cm; AC = 16 cm.
Tìm khẳng định sai trong các khẳng định sau?
Áp dụng định lí Pytago ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400 ⇒ BC = 20 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Câu 11: Cho tam giác ABC vuông tại A có BC = 26cm, AB = 10cm.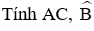 
(làm tròn đến độ)
Đáp án cần chọn là: C
Câu 12: Cho tam giác ABC có AB = 16, AC = 14 và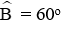 
. Tính BC
A. BC = 10
B. BC = 11
C. BC = 9
D. BC = 12
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
Đáp án cần chọn là: A
Câu 13: Cho tam giác ABC có AB = 12, AC = 15 và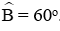 
. Tính BC
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
Đáp án cần chọn là: B
Câu 14: Cho tam giác ABC có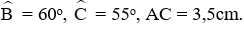 
Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
A. 4
B. 5
C. 7
D. 8
Kẻ đường cao AD
Xét tam giác vuông ACD, có AD = AC. sin C = 3,5. sin 50o ≈ 2,68cm
CD = AC. cos C = 3,5. cos 50o ≈ 2,25cm
Xét tam giác vuông ABD có BD = AD. cot B ≈ 2,68. cot 60o ≈ 1,55cm
Suy ra BC = BD + CD = 3,8
Đáp án cần chọn là: B
Câu 15: Cho tam giác ABC có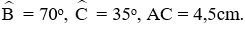 
Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)
A. 4
B. 5
C. 6
D. 8
Kẻ đường cao AD
Xét tam giác vuông ACD, có AD = AC.sin C = 4,5. sin 35o ≈ 2,58 cm
CD = AC. cos C = 4,5. cos 35o ≈ 3,69 cm
Xét tam giác vuông ABD, có BD = AD. cot B ≈ 2,58. cot 70o ≈ 0,94 cm
Suy ra BC = BD + DC = 0,94 + 3,69 = 4,63
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
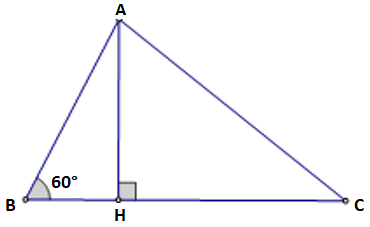
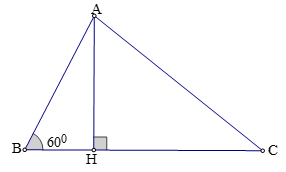
Câu 1: Cho tam giác ABC có AB = 16, AC = 14 và ∠B = 60°.
a) Tính độ dài cạnh BC.
b) Tính diện tích tam giác ABC.
Lời giải:
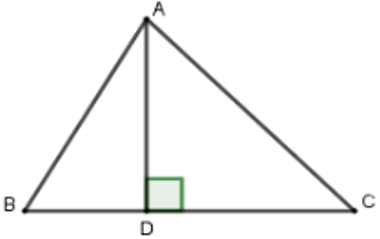
a) Kẻ đường cao AH.
Xét tam giác vuông ABH, ta có: BH = AB.cosB = AB.cos60° = 16.(1/2) = 8.
AH = AB.sinB = AB.sin60° = 16.(√3)/2 = 8√3
Áp dụng định lý Py – ta – go vào tam giác vuông AHC ta có:
HC2 = AC2 - AH2 = 142 - (8√3)2 = 196 - 192 = 4. Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
b) Ta có:
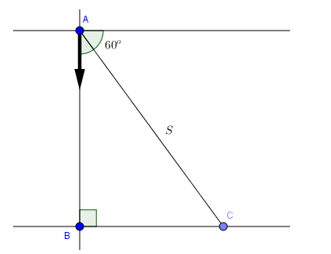
Câu 2: Một con thuyền băng qua một khúc sông với vận tốc là 3 km/h trong vòng 6 phút. Biết rằng hướng thuyền đi tạo với bờ một góc 60 độ. Tính chiều dài (m) của khúc sông đó.
Lời giải:
Ta giải bài toán thông qua hình vẽ trên
Nhận thấy ∠BAC = 30o
Ta đổi: 3(km/h) = 5/6(m/s); 6 phút = 360 giây
Khi đó ta có: S = (5/6). 360 = 300(m)
III. Bài tập vận dụng
Câu 1: Tính diện tích tam giác ABC biết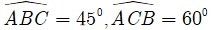 
bán kính đường tròn ngoại tiếp tam giác ABC là R.
Câu 2: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c. Chứng minh rằng:
a) a2 = b2 + c2 - 2bccosA
b) Gọi D là chân đường phân giác trong góc A . Chứng minh:
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Ứng dụng thực tế các tỉ số lượng giác của góc nhọn
Bài tập Ôn tập chương 1 hình học
Bài tập Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9