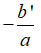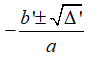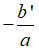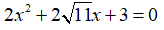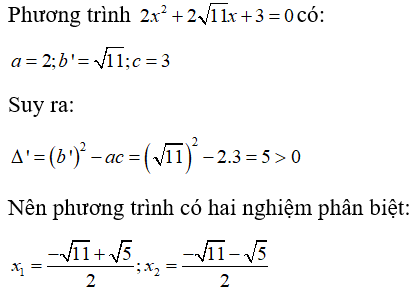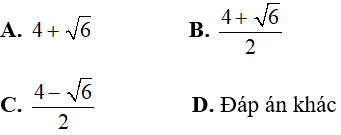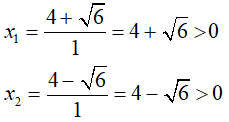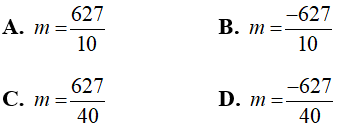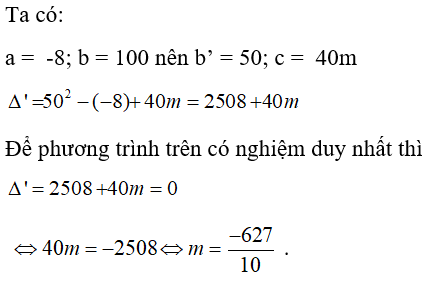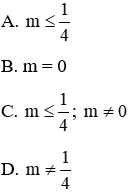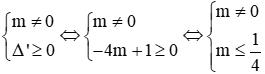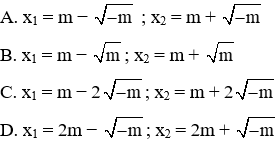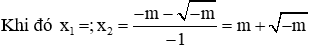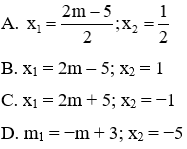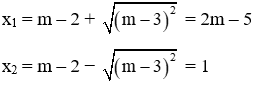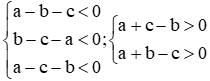50 Bài tập Công thức nghiệm thu gọn Toán 9 mới nhất
Với 50 Bài tập Công thức nghiệm thu gọn Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Công thức nghiệm thu gọn - Toán 9
I. Bài tập trắc nghiệm
Câu 1: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac. Phương trình đã cho có hai nghiệm phân biệt khi:
A. Δ' > 0
B. Δ' = 0
C. Δ' ≥ 0
D. Δ' ≤ 0
Lời giải:
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac:
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép x1 = x2 =
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt x1,2 =
Chọn đáp án A.
Câu 2: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac. Nếu Δ' = 0 thì:
A. Phương trình có hai nghiệm phân biệt
B. Phương trình có nghiệm kép x1 = x2 = Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án
C. Phương trình có nghiệm kép x1 = x2 = Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án
D. Phương trình có nghiệm kép x1 = x2 = Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án
Lời giải:
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac:
Nếu Δ' = 0 thì phương trình có nghiệm kép x1 = x2 =
Chọn đáp án C.
Câu 3: Tính Δ' và tìm số nghiệm của phương trình 7x2 - 12x + 4 = 0
A. Δ' = 6 và phương trình có hai nghiệm phân biệt
B. Δ' = 8 và phương trình có hai nghiệm phân biệt
C. Δ' = 8 và phương trình có nghiệm kép
D. Δ' = 0 và phương trình có hai nghiệm phân biệt
Lời giải:
Phương trình 7x2 - 12x + 4 = 0 có a = 7; b' = -6; c = 4 suy ra:
Δ' = (b')2 - ac = (-6)2 - 4.7 = 8 > 0
Nên phương trình có hai nghiệm phân biệt.
Chọn đáp án B.
Câu 4: Tìm m để phương trình 2mx2 - (2m + 1)x - 3 = 0 có nghiệm là x = 2
Chọn đáp án C.
Câu 5: Tính Δ' và tìm nghiệm của phương trình
Chọn đáp án D.
Câu 6: Tìm nghiệm dương của phương trình: x2 - 8x + 10 = 0
Ta có: a = 1; b = - 8 nên b’ = -4; c = 10.
Δ' = (-4)2 - 1.10 = 16 - 10 = 6
Do đó, phương trình đã cho có hai nghiệm phân biệt là;
Vậy cả hai nghiệm trên đều là nghiệm dương của phương trình đã cho.
Chọn đáp án D.
A. m = 3
B. m = 6
C. m = 9
D. m = -2
Ta có: a = 2 ; b = -10 nên b’ = -5; c = m + 1
Δ' = (-5)2 - 2.(m + 1) = 25 - 2m - 2 = 23 - 2m
Để Δ' = 11 thì 23 – 2m = 11
⇔ -2m = -12 ⇔ m = 6
Chọn đáp án B.
Câu 8: Cho phương trình 2x2 – 4x + m = 0. Tìm m để phương trình trên vô nghiệm?
A. m < 3
B. m > - 3
C. m > 2
D. m < -2
Ta có: a = 2; b = - 4 nên b’ = -2 và c = m
Δ' = (-2)2 - 2m = 4 - 2m
Để phương trình đã cho vô nghiệm thì:4 – 2m < 0 hay m > 2 .
Chọn đáp án C.
Câu 9: Cho hai phương trình x2 – 4x + 4= 0 và x2 + (m + 1)x + m = 0 . Tìm m để hai phương trình trên có nghiệm chung?
A. m = 2 hoặc m = -1
B. m = 1 hoặc m = 2
C. m = -1
D. m = -2
* Xét phương trình : x2 – 4x + 4= 0
⇔ (x-2)2 = 0 ⇔ x - 2 = 0 ⇔ x = 2
Vậy phương trình này có nghiệm duy nhất.
Để hai phương trình đã cho có nghiệm chung khi và chỉ khi x = 2 là nghiệm phương trình
x2 + (m + 1)x + m = 0.Suy ra:
22 + (m + 1).2 + m = 0
⇔ 4 + 2m + 2 + m = 0 ⇔ 6 + 3m = 0
⇔ 3m = +6 ⇔ m = -2
Chọn đáp án D.
Câu 10: Cho phương trình: -8x2 + 100x + 40m = 0. Tìm m để phương trình trên có nghiệm duy nhất?
Chọn đáp án B.
Câu 11: Tìm các giá trị của m để phương trình mx2 – 2(m – 1)x + m + 2 = 0 có nghiệm.
Phương trình mx2 – 2(m – 1)x + m + 2 = 0 có a = m; b’ = − (m – 1); c = m + 2
Suy ra ∆' = (m – 1)2 – m(m + 2) = −4m + 1
TH1: m = 0, ta có phương trình 2x + 2 = 0 ⇔ x = −1
TH2: m ≠ 0. Phương trình có nghiệm khi
Kết hợp cả hai trường hợp ta có với 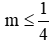
Đáp án cần chọn là: A
Câu 12: Phương trình (m – 3)x2 – 2(3m + 1)x + 9m – 1 = 0 có nghiệm khi?
Phương trình (m – 3)x2 – 2(3m + 1)x + 9m – 1 = 0 có a = m – 3; b’ = − (3m + 1) và c = 9m – 1
TH1: Nếu m – 3 = 0 ⇒ m = 3 thì phương trình (m – 3)x2 – 2(3m + 1)x + 9m – 1 = 0 trở thành −2(3.3 + 1) x + 9.3 – 1 = 0 ⇒ −20x + 26 = 0 ⇒ 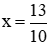
Vậy m = 3 thì phương trình có nghiệm duy nhất nên ta nhận m = 3
TH2: m ≠ 3 thì phương trình là phương trình bậc hai. Phương trình có nghiệm khi
Đáp án cần chọn là: A
Câu 13: Trong trường hợp phương trình −x2 + 2mx − m2 – m = 0 có hai nghiệm phân biệt. Hai nghiệm của phương trình là?
Phương trình −x2 + 2mx − m2 – m = 0 có a = −1; b’ = m; c = −m2 – m
Suy ra ∆' = m2 – (−1).( −m2 – m) = −m
Phương trình có hai nghiệm phân biệt khi –m > 0 ⇔ m < 0
Đáp án cần chọn là: A
Câu 14: Trong trường hợp phương trình x2 – 2(m – 2)x + 2m − 5 = 0 có hai nghiệm phân biệt. Hai nghiệm của phương trình là?
Phương trình x2 – 2(m – 2)x + 2m − 5 = 0 có a = 1; b’ = − (m – 2); c = 2m – 5
Suy ra ∆' = [− (m – 2)]2 – 1.(2m − 5) = m2 – 6m + 9 = (m – 3)2
Để phương trình có hai nghiệm phân biệt thì ∆' > 0 ⇔ (m – 3)2 > 0 ⇔ m ≠ 3
Khi đó, phương trình có hai nghiệm phân biệt là:
Đáp án cần chọn là: B
Câu 15: Cho phương trình x2 + (a + b + c)x + (ab + bc + ca) = 0 với a, b, c là ba cạnh của một tam giác. Khẳng định nào sau đây là đúng?
A. Phương trình luôn có hai nghiệm phân biệt
B. Phương trình luôn có nghiệm kép
C. Chưa đủ điều kiện để kết luận
D. Phương trình luôn vô nghiệm
Phương trình x2 + (a + b + c)x + (ab + bc + ca) = 0
Có ∆ = (a + b + c)2 − 4(ab + bc + ca) = a2 + b2 + c2 – 2ab – 2bc – 2ac
= (a – b)2 – c2 + (b – c)2 – a2 + (a – c)2 – b2
= (a – b – c)(a + c – b) + (b – c – a)(a + b – c) + (a – c – b)(a – c + b)
Mà a, b, c là ba cạnh của một tam giác nên
Nên ∆ < 0 với mọi a, b, c
Hay phương trình luôn vô nghiệm với mọi a, b, c
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Giải phương trình 2x2 - 6x + 4 = 0
Lời giải:
+ Tính Δ' = (-3)2 - 2.4 = 9 - 8 = 1 > 0
+ Do Δ' > 0, phương trình đã cho có hai nghiệm phân biệt là
Vậy phương trình đã cho có hai nghiệm là x1 = 2; x2 = 1.
Câu 2: Giải phương trình 3x2 - 6x + 3 = 0
Lời giải:
+ Tính Δ' = (-3)2 - 3.3 = 9 - 9 = 0
+ Do Δ' = 0, phương trình có nghiệm kép là x1 = x2 = -(-3/3) = 1
Vậy phương trình có nghiệm kép là x1 = x2 = 1
Câu 3: Giải phương trình 5x2 - 2x + 3 = 0
Lời giải:
+ Tính Δ' = (-1)2 - 5.3 = -14 < 0
+ Do Δ' < 0 nên phương trình đã cho vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
III. Bài tập vận dụng
Câu 1: Tìm giá trị của tham số m để phương trình x2 + 2mx + m - 4 = 0 có nghiệm.
Câu 2: Tìm giá trị của tham số m để phương trình x2 - mx + m - 1 = 0 có đúng một nghiệm duy nhất?
Câu 3: Giải các phương trình sau bằng công thức thu gọn:
3x2 + 18x + 29 = 0; x2 - 16x + 64 = 0
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Hệ thức Vi-ét và ứng dụng
Bài tập Phương trình quy về phương trình bậc hai
Bài tập Giải bài toán bằng cách lập phương trình
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9