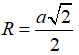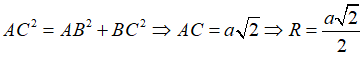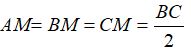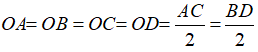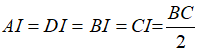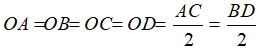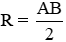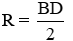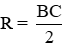50 Bài tập Sự xác định đường tròn. Tính chất đối xứng của đường tròn Toán 9 mới nhất
Với 50 Bài tập Sự xác định đường tròn. Tính chất đối xứng của đường tròn Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Sự xác định đường tròn. Tính chất đối xứng của đường tròn- Toán 9
I. Bài tập trắc nghiệm
Câu 1: Số tâm đối xứng của đường tròn là
A. 1
B. 2
C. 3
D. 4
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn
Chọn đáp án A
Câu 2: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
A. Đường tròn không có trục đối xứng
B. Đường tròn có duy nhất một trục đối xứng là đường kính
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
D. Đường tròn có vô số trục đối xứng là đường kính
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Chọn đáp án D
Câu 3: Tâm của đường tròn ngoại tiếp tam giác là
A. Giao của ba đường phân giác
B. Giao của ba đường trung trực
C. Giao của ba đường cao
D. Giao của ba đường trung tuyến
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó
Chọn đáp án B
Câu 4: Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn
B. Điểm M nằm trên đường tròn
C.Điểm M nằm trong đường tròn
D. Điểm M không thuộc đường tròn
Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:
Chọn đáp án B
Câu 5: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a
A. Tâm là giao điểm A và bán kính R = a√2
B. Tâm là giao điểm hai đường chéo và bán kính R = a√2
C. Tâm là giao điểm hai đường chéo và bán kính
D. Tâm là điểm B và bán kính là
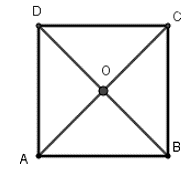
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Chọn đáp án C
Câu 6: Cho tam giác ABC vuông tại A. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là?
A. Điểm A
B. Điểm B .
C. Chân đường cao hạ từ A
D. Trung điểm của BC
Gọi M là trung điểm của BC.
Tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên:
Suy ra, điểm M là tâm đường tròn ngoại tiếp tam giác ABC
Chọn đáp án D.
Câu 7: Cho tứ giác ABCD là hình bình hành và 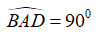
A. Trung điểm AC B . Điểm A
C. Điểm B
D. Điểm D
Vì tứ giác ABCD là hình bình hành và 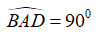
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Chọn đáp án A.
Câu 8: Cho 4 điểm phân biệt A, B, C và D sao cho tam giác ABC vuông tại A và tam giác BCD vuông tại
D. Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
A. Điểm A
B. Điểm B
C. Trung điểm BC
D. Trung điểm AD
Gọi I là trung điểm BC.
Ta có; tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
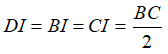
Tam giác ABC vuông tại A có AI là đường trung tuyến ứng với cạnh huyền BC nên:
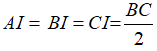
Từ (1) và (2) suy ra:
Do đó, I là tâm đường tròn ngoại tiếp tứ giác ABCD.
Chọn đáp án C
Câu 9: Cho hình thoi ABCD có AC = BD . Tìm tâm đường tròn ngoại tiếp hình thoi ABCD ?
A. Điểm A.
B. Giao điểm của AC và BD
C. Không có đường tròn ngoại tiếp tứ giác ABCD.
D. Trung điểm cạnh AB.
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Chọn đáp án B
Câu 10: Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm ........
A. có khoảng cách đến điểm I bằng 4cm
B. Có khoảng cách đến điểm I nhỏ hơn 4 cm.
C. Có khoảng cách đến điểm I lớn hơn 4 cm.
D. có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Chọn đáp án D.
Câu 11: Tâm của đường tròn ngoại tiếp tam giác vuông là:
A. Trung điểm cạnh huyền
B. Trung điểm cạnh góc vuông lớn hơn
C. Giao ba đường cao
D. Giao ba đường trung tuyến
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Đáp án cần chọn là: A
Câu 12: Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông?
A. bằng cạnh nhỏ nhất của tam giác vuông
B. bằng nửa cạnh góc vuông lớn hơn
C. bằng nửa cạnh huyền
D. bằng 4cm
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Do đó bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền
Đáp án cần chọn là: C
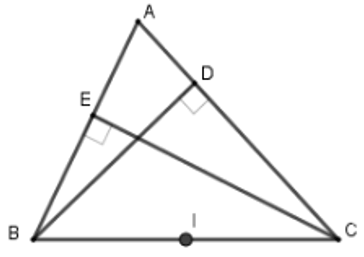
Câu 13: Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
A. Tâm là trọng tâm tam giác ABC và bán kính 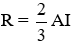
B. Tâm là trunng điểm AB và bán kính
C. Tâm là giao điểm của BD và EC, bán kính
D. Tâm là trung điểm BC và bán kính
Gọi I là trung điểm của BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Đáp án cần chọn là: D
Câu 14: Cho tam giác ABC có các đường cao BD, CE. Chọn khẳng định đúng.
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn
B. Năm điểm A, B, E, D, C cùng nằm trên một đường tròn
C. Cả A, B, đều sai
D. Cả A, B đều đúng
Gọi I là trung điểm BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Ta thấy IA > ID nên điểm A không thuộc đường tròn trên
Đáp án cần chọn là: A
Câu 15: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−1; −1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2
A. Điểm A nằm ngoài đường tròn
B. Điểm A nằm trên đường tròn
C. Điểm A nằm trong đường tròn
D. Không kết luận được
Lời giải:
Ta có 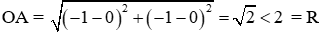
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
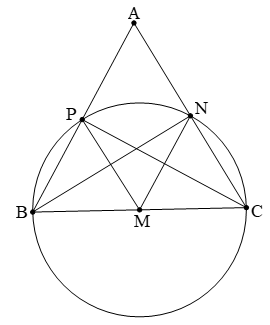
Câu 1: Cho tam giác đều ABC có cạnh bằng a. AB, BN, CP là các đường trung tuyến. Chứng minh 4 điểm B, P, N, C cùng thuộc một đường tròn. Tính bán kính đường tròn đó.
Lời giải:
Vì tam giác ABC đều nên các trung tuyến đồng thời cũng là đường cao .
Suy ra AM, BN, CP lần lượt vuông góc với BC, AC, AB.
Từ đó ta có các tam giác BPC, BNC là tam giác vuông với BC là cạnh huyền
Tam giác BPC vuông tại P có đường trung tuyến PM nên PM = BM = MC = 1/2 BC (1)
Tam giác BNC vuông tại N có đường trung tuyến NM nên NM = MB = MC = 1/2 BC (2)
Từ (1) và (2) suy ra: PM = NM = MB = MC = 1/2 BC
Hay: Các điểm B, P, N, C cùng thuộc đường tròn
Đường kính BC = a, tâm đường tròn là trung điểm M của BC
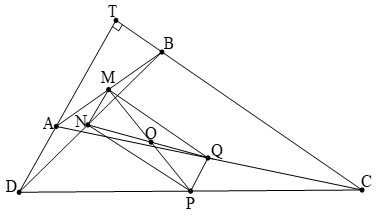
Câu 2: Cho tứ giác ABCD có ∠C + ∠D = 90°. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó .
Lời giải:
Kéo dài AD, CB cắt nhau tại điểm T thì tam giác TCD vuông tại T.
+ Do MN là đường trung bình của tam giác ABD nên NM // AD
+ MQ là đường trung bình của tam giác ABC nên MQ // BC. Mặt khác AD ⊥ BC ⇒ MN ⊥ MQ.
Chứng minh tương tự ta cũng có: MN ⊥ NP, NP ⊥ PQ. Suy ra MNPQ là hình chữ nhật.
Hay các điểm M, N, P, Q thuộc một đường tròn có tâm là giao điểm O của hai đường chéo NQ, MP
III. Bài tập vận dụng
Câu 1: Chứng minh rằng đường tròn ngoại tiếp tam giác vuông có tâm chính là trung điểm của cạnh huyền
Câu 2: Cho hình chữ nhật ABCD có AB = 10, BC = 8 . Chứng minh rằng A, B, C, D cùng thuộc một đường tròn và tính bán kính của đường tròn đó
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Đường kính và dây của đường tròn
Bài tập Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài tập Vị trí tương đối của đường thẳng và đường tròn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9