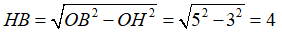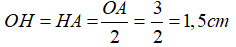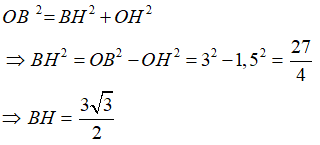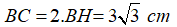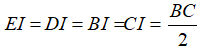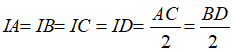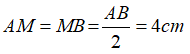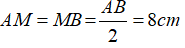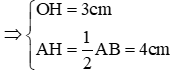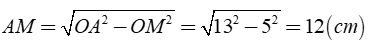50 Bài tập Đường kính và dây của đường tròn Toán 9 mới nhất
Với 50 Bài tập Đường kính và dây của đường tròn Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Đường kính và dây của đường tròn - Toán 9
I. Bài tập trắc nghiệm
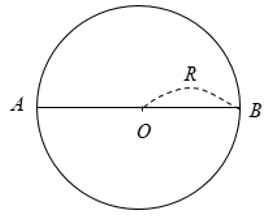
Câu 1: Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
A. AB > CD
B. AB = CD
C. AB < CD
D. AB ≤ CD
Trong các dây của đường tròn, dây lớn nhất là đường kính
Chọn đáp án A.
Câu 2: Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng
A. AB > CD
B. AB = CD
C. AB < CD
D. AB // CD
Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau
Chọn đáp án B.
Câu 3: “Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp
A. nhỏ hơn
B. bằng
C. song song
D. vuông góc
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
Chọn đáp án D.
Câu 4: Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
A. Dây nào lớn hơn thì dây đó xa tâm hơn
B. Dây nào nhỏ hơn thì đây đó xa tâm hơn
C. Dây nào gần tâm hơn thì dây đó lớn hơn
D. Hai dây bằng nhau thì cách đều tâm
Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm
- Trong hai dây của đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn
+ Dây nào gần tâm hơn thì dây đó lớn hơn
Nên phương án B, C, D đúng
Chọn đáp án A.
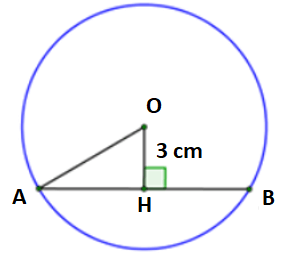
Câu 5: Cho đường tròn (O) có bán kính R = 5 cm. Khoảng cách từ tâm đến dây AB là 3 cm. Tính độ dài dây AB
A. AB = 6 cm
B. AB = 8 cm
C. AB = 10 cm
D. AB = 12 cm
Kẻ OH ⊥ AB tại H suy ra H là trung điểm của AB
Xét tam giác OHB vuông tại H có OH = 3; OB = 5 . Theo định lý Pytago ta có:
Mà H là trung điểm của AB nên AB = 2HB = 8 cm
Vậy AB = 8 cm
Chọn đáp án B.
Câu 6: Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính BC.
Gọi H là trung điểm của BC.
Do dây BC vuông góc với OA tại H nên ta có:
Áp dụng định lí Pytgo vào tam giác OHB vuông tại H ta có:
Theo định lí quan hệ vuông góc đường kính và dây ta có: H là trung điểm BC nên:
Chọn đáp án A.
Câu 7: Cho ΔABC, các đường cao BD và CE. Tìm mệnh đề sai
A. Bốn điểm B, E, D và C cùng nằm trên một đường tròn.
B. DE < BC.
C. Tâm đường tròn ngoại tiếp tứ giác BCDE là trung điểm BC
D. Tất cả sai.
Gọi I là trung điểm BC.
Tam giác BCE vuông tại E có đường trung tuyến EI ứng với cạnh huyền BC nên:
(1)
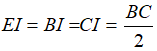
Tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
(2)
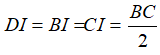
Từ ( 1) và (2) suy ra: 
Do đó, I là tâm đường tròn ngoại tiếp tứ giác BCDE.
Khi đó, BC là đường kính và DE là dây không đi qua tâm nên: BC > DE.
Chọn đáp án D.
Câu 8: Cho hình chữ nhật ABCD. Tìm khẳng định đúng
A. AC < BD
B. AB > AC
C. AC > CD
D. AB > BC
Gọi I là giao điểm hai đường chéo AC và BD,
Theo tính chất hình chữ nhật ta có:
Do đó, I là tâm đường tròn ngoại tiếp hình chữ nhật ABCD có AC và BD là đường kính.
AB, BC, CD và DA là các dây.
Chọn đáp án C.
Câu 9: Cho đường tròn tâm O , bán kính R = 5cm , có dây AB = 8cm và M là trung điểm của AB. Tính khoảng cách từ O đến AB ?
A. 3cm
B. 4cm
C. 2cm
D. 5 cm
Vì M là trung điểm của AB nên ta có: 
Theo quan hệ vuông góc giữa đường kính và dây ta có:
OM ⊥ AB
Áp dụng định lí Pytago vào tam giác OAM ta có:
OM2 = OA2 - AM2 = 52 - 42 = 9 ⇒ OM = 3 cm
Chọn đáp án A.
Câu 10: Cho đường tròn tâm O có dây AB = 16cm. Gọi M là trung điểm AB. Biết khoảng cách từ O đến AB bằng 6. Tính bán kính đường tròn.
A. 7cm
B. 8cm
C. 10cm
D. 12 cm
Vì M là trung điểm của AB nên ta có: 
Theo quan hệ vuông góc giữa đường kính và dây ta có;
Mà khoảng cách từ O đến AM bằng 6 cm nên OM = 6 cm
Áp dụng định lí pytago vào tam giác OAM vuông ta có:
OA2 = OM2 + AM2 = 62 + 82 = 100 nên OA = 10 cm
Suy ra: bán kính đường tròn đã cho là R = 10 cm.
Chọn đáp án C.
Câu 11: Cho đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt A, B. Biết khoảng cách từ điểm O đến đường thẳng d bằng 3cm và độ dài đoạn thẳng AB bằng 8cm. Bán kính của đường tròn (O) bằng:
A. 7cm
B. 11cm
C. 73cm
D. 5cm
Kẻ OH ⊥ AB. Khi đó H là trung điểm của AB (mối liên hệ giữa đường kính và dây cung) 
Áp dụng định lý Pytago cho ΔAOH vuông tại H ta có:
OA2 = AH2 + HO2 = 42 + 32 = 25 ⇒ R = OA = 5cm
Đáp án cần chọn là: D
Câu 12: Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2cm; IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:
A. 4cm
B. 1cm
C. 3cm
D. 2cm
Xét đường tròn tâm (O).
Kẻ OE ⊥ AB tại E suy ra E là trung điểm của AB, kẻ OF ⊥ CD tại F.
Vì dây AB = AC nên OE = OF (hai dây bằng nhau cách đều tâm)
Xét tứ giác OEIF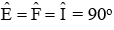 
nên OEIF là hình chữ nhật và OE = OF nên OEIF là hình vuông ⇒ OE = OF = EI
Mà AB = IA + IB = 6cm ⇒ EB = 3cm ⇒ EI = EB – IB = 1cm nên OE = OF = 1cm
Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 2cm
Đáp án cần chọn là: D
Câu 13: Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 6cm; IB = 3cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:
A. 4cm
B. 1cm
C. 3cm
D. 2cm
Xét đường tròn tâm (O)
Kẻ OE AB tại E suy ra E là trung điểm của AB, kẻ OF CD tại F.
Vì dây AB = AC nên OE = OF (hai dây bằng nhau cách đều tâm)
Xét tứ giác OEIF có 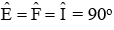nên OEIF là hình chữ nhật và OE = OF nên OEIF là hình vuông ⇒ OE = OF = EI
Mà AB = IA + IB = 9cm ⇒ EB = 4,5cm ⇒ EI = EB – IB = 1,5cm nên OE = OF = 1,5cm
Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 1,5 + 1,5 = 3cm
Đáp án cần chọn là: C
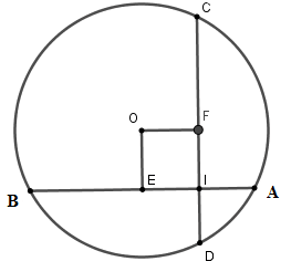
Câu 14: Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 16cm; CD = 12cm; MC = 2cm. Khoảng cách từ tâm O đến dây AB là?
A. 4cm
B. 5cm
C. 3cm
D. 2cm
Xét đường tròn tâm (O)
Kẻ OE ⊥ AB tại E suy ra E là trung điểm của AB, kẻ OF ⊥ CD tại F suy ra F là trung điểm CD
Xét tứ giác OEMF có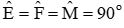 
nên OEIF là hình chữ nhật, suy ra FM = OE
Ta có CD = 12cm ⇒ FC = 6cm mà MC = 2cm ⇒ FM = FC – MC = 4cm nên
OE = 4cm
Vậy khoảng cách từ tâm O đến dây AB là 4cm
Đáp án cần chọn là: A
Câu 15: Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết CD = 8cm; MC = 1cm. Khoảng cách từ tâm O đến dây AB là?
A. 4cm
B. 5cm
C. 3cm
D. 2cm
Lời giải:
Kẻ OE ⊥ AB tại E suy ra E là trung điểm của AB, kẻ OF ⊥ CD tại F suy ra F là trung điểm CD
Xét tứ giác OEMF có 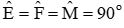nên OEIF là hình chữ nhật, suy ra FM = OE
Ta có CD = 8cm ⇒ FC = 4cm mà MC = 1cm ⇒ FM = FC – MC = 4 – 1 = 3cm
nên OE = FM = 3cm
Vậy khoảng cách từ tâm O đến dây AB là 3cm
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
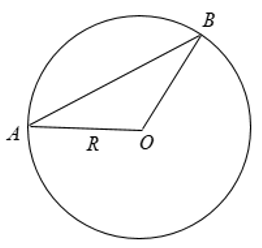
Câu 1: Gọi AB là một dây bất kỳ của đường tròn (O; R). Chứng minh rằng AB ≤ 2R
+ Trường hợp 1: AB là đường kính
⇒ AB = 2R
+ Trường hợp 2: AB không là đường kính
Xét tam giác AOB, áp dụng bất đẳng thức tam giác ta có:
AB < AO + OB = R + R = 2R
Vậy ta luôn có AB ≤ 2R
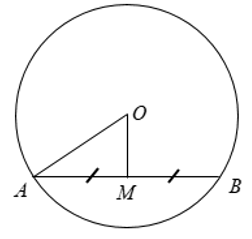
Câu 1: Cho hình vẽ sau, tính độ dài dây AB khi biết OA = 13cm; AM = MB; OM = 5cm.
Lời giải:
Áp dụng định lý: “ Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy “
Khi đó ta có: OM ⊥ AB.
Áp dụng định lý Py – ta – go ta có:
⇒ AB = 2.AM = 2.12 = 24 (cm)
III. Bài tập vận dụng
Câu 1: Cho tam giác ABC có đường cao là BD, CE. Chứng minh rằng B, D, C, E cùng một đường tròn và ED < BC .
Câu 2: Cho đường tròn tâm O đường kính AB, dây CD không cắt AB. Gọi H, K lần lượt là hình chiếu vuông góc của A, B lên CD. Chứng minh: CH = DK
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài tập Vị trí tương đối của đường thẳng và đường tròn
Bài tập Dấu hiệu nhận biết tiếp tuyến của đường tròn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9