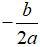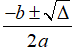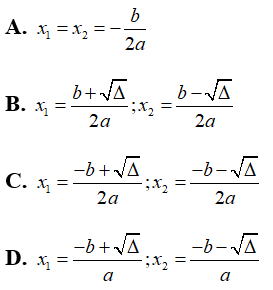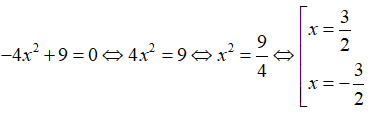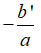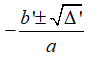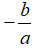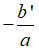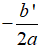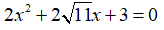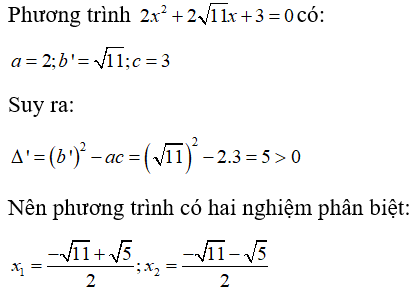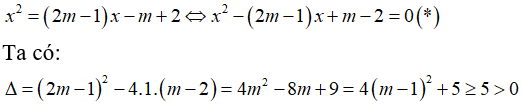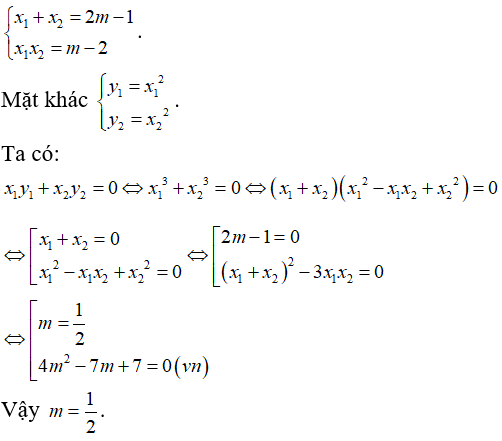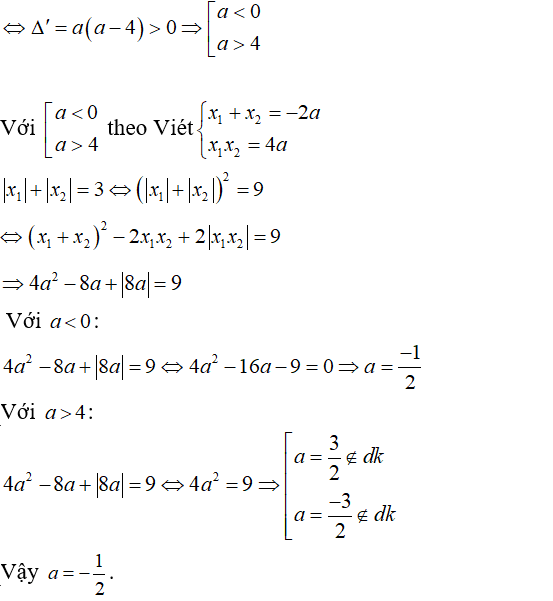50 Bài tập Ôn tập chương 4 Đại số Toán 9 mới nhất

 Bài tập Ôn tập chương 4 Đại số - Toán 9

I. Bài tập trắc nghiệm

Câu 1: Cho hàm số y = ax2 với a ≠ 0 . Kết luận nào sau đây là đúng:

A. Hàm số nghịch biến khi a > 0 và x > 0

B. Hàm số nghịch biến khi a < 0 và x < 0

C. Hàm số nghịch biến khi a > 0 và x < 0

D. Hàm số nghịch biến khi a > 0 và x = 0

Lời giải:

Cho hàm số • Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0 • Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0

Chọn đáp án C.

Câu 2: Kết luận nào sau đây sai khi nói về đồ thị hàm số y = ax2 với a ≠ 0

A. Đồ thị hàm số nhận trục tung làm trục đối xứng.

B. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị

C. Với a < 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị

D. Với a > 0 đồ thị nằm phía trên trục hoành và là O điểm thấp nhất của đồ thị

Lời giải:

Đồ thị hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol). • Nếu a < 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị • Nếu a > 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị

Chọn đáp án B.

Câu 3: Giá trị của hàm số y = f(x) = -7x2 tại x0 = -2 là:

A. 28

B. 12

C. 21

D. -28

Lời giải:

Thay x0 = -2 vào hàm số y = f(x) = -7x2 ta được: y = f(-2) = -7.(-2)2 = -28

Chọn đáp án D.

Câu 4: Cho hàm số y = f(x) = (-2m + 1)x2 . Tính giá trị của m để đồ thị đi qua điểm A(-2; 4)

A. m = 0

B. m = 1

C. m = 2

D. m = -2

Lời giải:

Thay tọa độ điểm A(-2; 4) vào hàm số y = f(x) = (-2m + 1)x2 ta được: (-2m + 1).(-2)2 = 4 ⇔ - 2m + 1 = 1 ⇔ m = 0 Vậy m = 0 là giá trị cần tìm.

Chọn đáp án A.

Câu 5: Cho hàm số y = f(x) = -2x2. Tổng các giá trị của a thỏa mãn f(a) = -8 + 4√3 là:

A. 1

B. 0

C. 10

D.

Lời giải:

Thay a vào hàm số y = f(x) = -2x2 ta được: 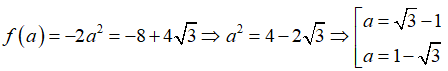 Tổng các giá trị của a là: √3 - 1 + 1 - √3 = 0

Chọn đáp án B.

Câu 6: Phương trình nào dưới đây là phương trình bậc hai một ẩn:

Lời giải:

Phương trình bậc hai một ẩn (hay gọi tắt là phương trình bậc hai) là phương trình có dạng: ax2 + bx + c = 0 (a ≠ 0) trong đó a, b, c là các số thực cho trước, x là ẩn số.

Chọn đáp án B.

Câu 7: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 - 4ac. Phương trình đã cho vô nghiệm khi:

A. Δ < 0

B. Δ = 0

C. Δ ≥ 0

D. Δ ≤ 0

Lời giải:

Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac

• TH1: Nếu thì phương trình vô nghiệm

• TH2: Nếu thì phương trình có nghiệm kép x1 = x2 = 

• TH3: Nếu thì phương trình có hai nghiệm phân biệt x1,2 = 

Chọn đáp án A.

Câu 8: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 - 4ac. Khi đó phương trình có hai nghiệm là:

Lời giải:

Xét phương trình bậc hai một ẩn và biệt thức

• TH1: Nếu thì phương trình vô nghiệm

• TH2: Nếu thì phương trình có nghiệm kép x1 = x2 = 

• TH3: Nếu thì phương trình có hai nghiệm phân biệt x1,2 = 

Chọn đáp án C.

Câu 9: Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6x2 - 7x = 0

Lời giải:

Ta có:

Chọn đáp án B.

Câu 10: Không dùng công thức nghiệm, tìm số nghiệm của phương trình -4x2 + 9 = 0

A. 0

B. 1

C. 3

D. 2

Lời giải:

Ta có:

Nên số nghiệm của phương trình là 2.

Chọn đáp án D.

Câu 11: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac. Phương trình đã cho có hai nghiệm phân biệt khi:

A. Δ' > 0

B. Δ' = 0

C. Δ' ≥ 0

D. Δ' ≤ 0

Lời giải:

Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac:

• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm

• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép x1 = x2 = 

• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt x1,2 = 

Chọn đáp án A.

Câu 12: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac. Nếu Δ' = 0 thì:

A. Phương trình có hai nghiệm phân biệt

B. Phương trình có nghiệm kép x1 = x2 = 

C. Phương trình có nghiệm kép x1 = x2 = 

D. Phương trình có nghiệm kép x1 = x2 = 

Lời giải:

Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac:

Nếu Δ' = 0 thì phương trình có nghiệm kép x1 = x2 = 

Chọn đáp án C.

Câu 13: Tính Δ' và tìm số nghiệm của phương trình 7x2 - 12x + 4 = 0

A. Δ' = 6 và phương trình có hai nghiệm phân biệt

B. Δ' = 8 và phương trình có hai nghiệm phân biệt

C. Δ' = 8 và phương trình có nghiệm kép

D. Δ' = 0 và phương trình có hai nghiệm phân biệt

Lời giải:

Phương trình 7x2 - 12x + 4 = 0 có a = 7; b' = -6; c = 4 suy ra:

Δ' = (b')2 - ac = (-6)2 - 4.7 = 8 > 0

Nên phương trình có hai nghiệm phân biệt.

Chọn đáp án B.

Câu 14: Tìm m để phương trình 2mx2 - (2m + 1)x - 3 = 0 có nghiệm là x = 2

Lời giải:

Chọn đáp án C.

Câu 15: Tính Δ' và tìm nghiệm của phương trình 

Lời giải:

Chọn đáp án D.

II. Bài tập tự luận có lời giải

Câu 1: Tìm hàm số y = ax2 biết đồ thị của nó đi qua điểm A(-1; 2) Với hàm số tìm được hãy tìm các điểm trên đồ thị có tung độ là 8.

Lời giải:

+ Ta có đồ thị hàm số y = ax2 đi qua điểm A(-1; 2) nên ta có:

2 = a.(-1)2 ⇔ a = 2

Vậy hàm số cần tìm là y = ax2

+ Các điểm trên đồ thị có tung độ là 8.

Gọi điểm cần tìm là M(x0; y0)

Ta có: y0 = 8 ⇒ 8 = 2.x02 ⇔ x02 = ±2

Vậy các điểm cần tìm trên đồ thị có tung độ là 8 là: M(-2; 8); M(2; 8)

Câu 2: Cho Parabol (P): y = x2 và đường thẳng d: (2m - 1)x - m + 2 (m là tham số)

a) Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt.

b) Tìm các giá trị của m để đường thẳng d luôn cắt (P) tại hai điểm phân biệt A(x1; y1), B(x2; y2) thỏa x1y1 + x2y2 .

Lời giải:

a) Phương trình hoành độ giao điểm

Do đó, phương trình (*) luôn có 2 nghiệm phân biệt với mọi m.

Vậy Parabol luông cắt đường thẳng tại hai điểm phân biệt.

b) Vì x1, x2 là nghiệm của phương trình (*) nên.

Câu 3: Cho parabol (P): y = x2 và đường thẳng (d): y = -2ax - 4a (với a là tham số )

a) Tìm tọa độ giao điểm của (d) và (P) khi a = - 1/2 .

b) Tìm tất cả các giá trị của a để đường thẳng (d) cắt (P) taị hai điểm phân biệt có hoành độ x1; x2 thỏa mãn |x1| + |x2| = 3 .

Lời giải:

a) Phương trình hoành độ (d) và (P) là x2 = -2ax - 4a

x2 + 2ax + 4a = 0

Khi a = - 1/2 thì phương trình trở thành x2 - x - 2 = 0

Có a - b + c = 0 nên phương trình có 2 nghiệm là x = -1; x = 2

* Với x = - 1 thì y = 1 ta được điểm A(-1; 1)

* Với x = 2 thì y = 4 ta được điểm B( 2; 4 ).

Vậy giao điểm cần tìm là: A(-1; 1); B(2; 4)

b) Phương trình hoành độ (d) và (P) là x2 + 2ax + 4a = 0 (*)

để đường thẳng (d) cắt (P) tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt

III. Bài tập vận dụng

Câu 1: Cho hai hàm số y = x2 và y = mx + 4, với m là tham số.

a) Khi m = 3 , tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị m , đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A1(x1; y1) và A2(x2; y2) Tìm tất cả các giá trị của m sao cho (y1)2 + (y2)2 = 72 .

Câu 2: Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án và hai điểm A, B thuộc (P) có hoành độ lần lượt là xA = -1, xB = 2

a) Tìm tọa độ của hai điểm A, B.

b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.

c) Tính khoảng cách từ điểm O (gốc tọa độ) tới đường thẳng (d) .

Câu 3: Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.

Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:

Bài tập Góc ở tâm, Số đo cung

Bài tập Liên hệ giữa cung và dây

Bài tập Góc nội tiếp

Bài tập Góc tạo bởi tia tiếp tuyến và dây cung

Bài tập Góc có đỉnh ở bên trong đường tròn, Góc có đỉnh ở bên ngoài đường tròn