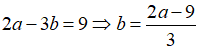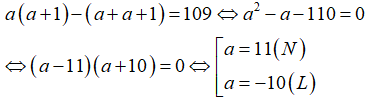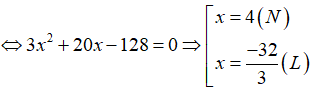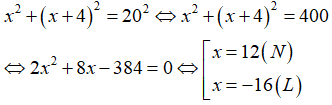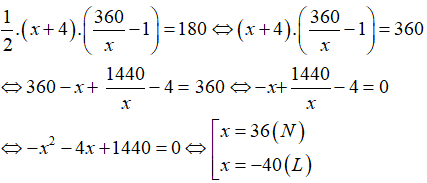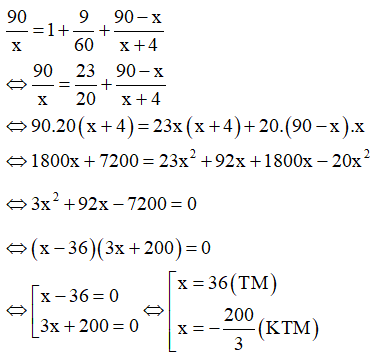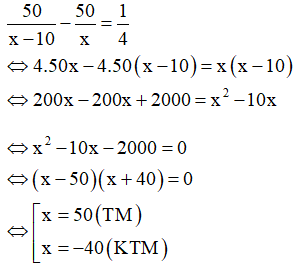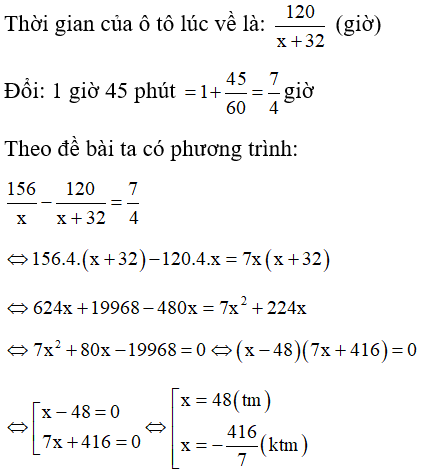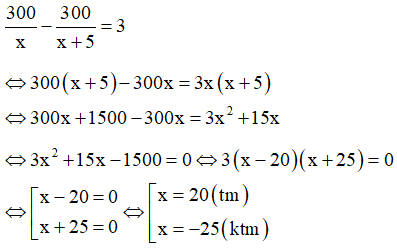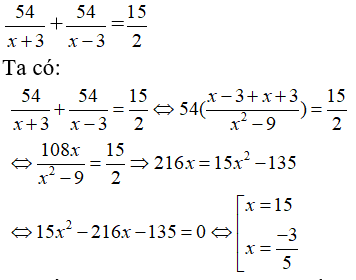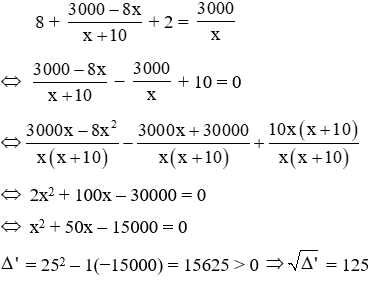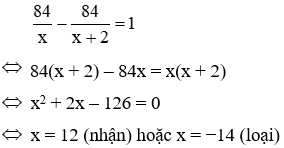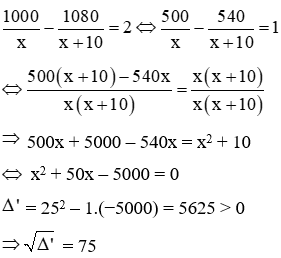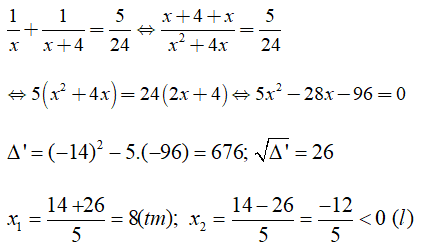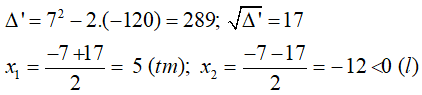50 Bài tập Giải bài toán bằng cách lập phương trình Toán 9 mới nhất
Với 50 Bài tập Giải bài toán bằng cách lập phương trình Toán lớp 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Giải bài toán bằng cách lập phương trình - Toán 9
I. Bài tập trắc nghiệm
Câu 1: Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.
A. 12
B. 13
C. 32
D. 33
Lời giải:
Gọi số thứ nhất là a; a ∈ N , số thứ hai là b; b ∈ N
Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
a2 – b2 = 119 hay
Chọn đáp án A.
Câu 2: Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm số bé hơn.
A. 12
B. 13
C. 32
D. 11
Lời giải:
Gọi số bé hơn là a; a ∈ N thì số lớn hơn là a + 1
Vì tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109 nên ta có phương trình:
Vậy số bé hơn là 11.
Chọn đáp án D.
Câu 3: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5cm thì được một hình chữ nhật mới có diện tích bằng 153 cm2. Tìm chu vi hình chữ nhật ban đầu.
A. 16
B. 32
C. 34
D. 36
Lời giải:
Gọi x là chiều rộng hình chữ nhật lúc đầu (x > 0) (cm)
Chiều dài hình chữ nhật lúc đầu: 3x (cm)
Chiều rộng hình chữ nhật lúc sau: x + 5 (cm)
Chiều dài hình chữ nhật lúc sau: 3x + 5 (cm)
Theo đề bài ta có phương trình: (x + 5)(3x + 5) = 153
Vậy chiều dài và chiều rộng hình chữ nhật ban đầu là: 12 cm và 4 cm
Suy ra chu vi hình chữ nhật ban đầu là: (12 + 4).2 = 32 (cm)
Chọn đáp án B.
Câu 4: Cho tam giác vuông có cạnh huyền bằng 20 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 4 cm. Một trong hai cạnh góc vuông của tam giác vuông có độ dài là:
A. 16
B. 15
C. 14
D. 13
Lời giải:
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm
Chọn đáp án A.
Câu 5: Một thửa ruộng hình tam giác có diện tích 180 cm2. Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm đi 1m thì diện tích không đổi.
A. 10
B. 35
C. 36
D. 18
Gọi độ dài cạnh đáy là x (cm) (x > 0)
Chiều cao của thửa ruộng có độ dài là: 360/x (cm)
Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:
Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm
Chọn đáp án C.
Câu 6: Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90 km trong một thời gian đã định. Sau khi đi được 1 giờ, ngườ đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng hẹn, người ấy phải tăng vận tốc thêm 4 km/h. Tính vận tốc lúc đầu của người đó.
A. 36 km / h
B. 40 km/ h
C. 45km/ h
D. 50km/ h
Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).
Thời giạn dự định người đó đi hết quãng đường là 90/x (h).
Quãng đường người đó đi được sau 1 giờ là x (km).
Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).
Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).
Thời gian người đó đi hết quãng đường còn lại là 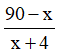
Theo đề bài ta có phương trình:
Vậy vận tốc lúc đầu của người đó là 36 km/h.
Chọn đáp án A.
Câu 7: Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến
B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc mỗi xe.
A. 40 và 30
B. 40 và 50
C. 50 và 60
D. 45 và 55
Gọi vận tốc của xe thứ nhất là x (km/h) (x > 10).
Vận tốc của xe thứ hai là x – 10 (km/h).
Thời gian xe thứ nhất đi từ A đến B là 50/x (h).
Thời gian xe thứ hai đi từ A đến B là 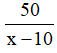
Vì xe thứ nhất đến B trước xe thứ hai 15 phút = 1/4 h nên ta có phương trình:
Vậy vận tốc của xe thứ nhất là 50 km/h, vận tốc của xe thứ hai là 40 km/h.
Chọn đáp án B.
Câu 8: Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36km so với lúc đi và vận tốc tăng so với lúc đi là 32km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.
A. 36 km/ h
B. 40km/h
C. 45km/ h
D. 48 km/ h
Gọi vận tốc của ô tô khi đi từ A đến B là x (km/h) (x > 0)
Thời gian ô tô đi từ A đến B là: 156/x (giờ)
Vận tốc của ô tô lúc về là: x + 32 (km) .
Vậy vận tốc của ô tô lúc đi từ A đến B là 48km/h
Chọn đáp án D.
Câu 9: Để phục vụ cho Festival Huế 2018, một cơ sở sản xuất nón lá dự kiến làm ra 300 chiếc nón lá trong một thời gian đã định. Do được bổ sung thêm nhân công nên mỗi ngày cơ sở đó làm ra được nhiều hơn 5 chiếc nón lá so với dự kiến ban đầu, vì vậy cơ sở sản xuất đã hoàn thành 300 chiếc nón lá sớm hơn 3 ngày so với thời gian đã định. Hỏi theo dự kiến ban đầu, mỗi ngày cơ sở đó làm được ra bao nhiêu chiếc nón lá? Biết rằng số chiếc nón lá làm ra mỗi ngày là bằng nhau và nguyên chiếc.
A. 10
B. 15
C. 20
D. 25
Gọi số chiếc nón lá mỗi ngày cơ sở đó làm được là x (chiếc)
Số ngày cơ sở đó dự kiến làm hết 300 chiếc nón lá là: 300/x (ngày)
Sau khi làm tăng thêm 5 chiếc nón lá một ngày thì thời gian cơ sở đó làm hết 300 chiếc nón lá là: 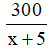
Theo đề bài ta có phương trình:
Vậy theo dự kiến, mỗi ngày cơ sở đó làm được 20 chiếc nón lá.
Chọn đáp án C.
Câu 10: Một ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút. Tính vận tốc thực của ca nô biết quãng đường sông AB dài 54 km và vận tốc dòng nước là 3 km/h.
Đổi 7 giờ 30 phút= 15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h; x > 3).
vận tốc của ca nô khi xuôi dòng sông từ A đến B là: x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là: x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là: 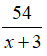
Thời gian của ca nô khi ngược dòng sông từ B về A là: 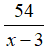
Do ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
Ta thấy chỉ có x = 15 thỏa mãn điều kiện x > 3.
Vậy vận tốc thực của ca nô là 15 (km/h).
Câu 11: Một công nhân dự định làm 120 sản phẩm trong một thời gian dự định. Sau khi làm được 2 giờ với năng suất dự kiến, người đó đã cải tiến các thao tác hợp lý hơn nên tăng năng suất thêm 3 sản phẩm mỗi giờ và vì vậy người đó hoàn thành kế hoạch sớm hơn dự định 1 giờ 36 phút. Hãy tính năng suất dự kiến.
A. 10
B. 14
C. 12
D. 18
Gọi năng suất dự định là x (0 < x < 20, sản phẩm/giờ)
Sản phẩm làm được sau 2 giờ là: 2x (sản phẩm)
Số sản phẩm còn lại là 120 – 2x (sản phẩm)
Năng suất sau khi cải tiến là x + 3 (sản phẩm/giờ)
Thời gian làm số sản phẩm còn lại là: 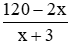
Do sau khi cải tiến người đó hoàn thành kế hoạch sớm hơn dự định 1 giờ 36 phút
Đổi 1 giờ 36 phút bằng 1,6 giờ
Vậy năng suất dự định của công nhân đó là 12 sản phẩm/giờ
Đáp án cần chọn là: C
Câu 12: Một nhóm thợ phải thực hiện kế hoạch sản xuất 3000 sản phẩm. Trong 8 ngày đầu, họ thực hiện đúng mức đề ra, những ngày còn lại họ vượt mức mỗi ngày 10 sản phẩm nên đã hoàn thành sớm hơn dự định 2 ngày. Hỏi theo kế hoạch cần sản xuất mỗi ngày bao nhiêu sản phẩm.
A. 100 sản phẩm
B. 200 sản phẩm
C. 300 sản phẩm
D. 400 sản phẩm
Gọi số sản phẩm nhóm thợ theo kế hoạch phải làm mỗi ngày là x (x ∈ N*)
+) Theo kế hoạch: Thời gian hoàn thành là 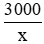
+) Thực tế:
Số sản phẩm làm trong 8 ngày là 8x (sản phẩm)
Số sản phẩm còn lại là 3000 – 8x (sản phẩm)
Mỗi ngày sau đó nhóm thợ làm được x + 10 (sản phẩm)
Thời gian hoàn thành 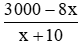
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
Phương trình có hai nghiệm phân biệt: x1 = − 25 – 125 = −150 (loại) và
x2 = −25 + 125 = 100 (tmđk)
Vậy theo kế hoạch, mỗi ngày cần làm 100 sản phẩm
Đáp án cần chọn là: A
Câu 13: Theo kế hoạch một người công nhân phải hoàn thành 84 sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật nên thực tế mỗi giờ người đó đã làm được nhiều hơn 2 sản phẩm so với số sản phẩm phải làm trong một giờ theo kế hoạch. Vì vậy người đó hoàn thành công việc sớm hơn dự định 1 giờ. Hỏi theo kế hoạch, mỗi giờ người công nhân phải làm bao nhiêu sản phẩm.
A. 16
B. 12
C. 14
D. 18
Gọi x là số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo kế hoạch (x ∈ N*, x < 84)
Số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo thực tế: x + 2
Thời gian mà công nhân hoàn thành theo kế hoạch: 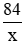
Thời gian mà công nhân hoàn thành theo thực tế: 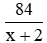
Người công nhân đó hoàn thành công việc sớm hơn dự định 1 giờ nên ta có phương trình:
Vậy theo kế hoạch mỗi giờ người công nhân phải làm 12 sản phẩm
Đáp án cần chọn là: B
Câu 14: Một đội sản xuất phải làm 1000 sản phẩm trong một thời gian quy định. Nhờ năng năng suất nên mỗi ngày đội làm thêm được 10 sản phẩm so với kế hoạch. Vì vậy, chẳng những đã làm vượt mức kế hoạch 80 sản phẩm mà còn hoàn thành sớm hơn 2 ngày so với quy định. Tính số sản phẩm mà đội phải làm trong 1 ngày theo kế hoạch.
A. 60 sản phẩm
B. 70 sản phẩm
C. 50 sản phẩm
D. 80 sản phẩm
Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ N*, x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 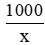
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 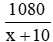
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
Phương trình có hai nghiệm phân biệt: x1 = − 25 – 75 = −100 (loại)
và x2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án cần chọn là: C
Câu 15: Một xưởng có hế hoạch in xong 6000 quyển sách giống nhau trong một thời gian quy định, biết số quyển sách in được trong một ngày là bằng nhau. Để hoàn thành sớm kế hoạch, mỗi ngày xưởng đã in nhiều hơn 300 quyển sách so với số quyển sách phải in trong kế hoạch, nên xưởng in xong 6000 quyển sách nói trên sớm hơn kế hoạch 1 ngày. Tính số quyển sách xưởng in được trong 1 ngày theo kế hoạch.
A. 1600
B. 3000
C. 1400
D. 1200
Gọi x (quyển sách) là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch (x ∈ N*)
Số ngày in theo kế hoạch: 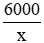
Số quyển sách xưởng in được thực tế trong mỗi ngày: x + 300 (quyển sách)
Số ngày in thực tế: 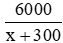
Vậy số quyển sách xưởng in được trong mỗi ngày theo kế hoạch là: 1200 (quyển sách)
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Cho một bể cạn (không có nước). Nếu hai vòi nước cùng được mở để chảy vào bể này thì sẽ đầy bể sau 4 giờ 48 phút. Nếu mở riêng từng vòi chảy vào bể thì thời gian vòi một chảy đầy bể sẽ ít hơn thời gian vòi hai chảy đầy bể là 4 giờ. Hỏi mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể?
Lời giải:
Đổi 4 giờ 48 phút = 24/5 (giờ)
Gọi thời gian vòi một chảy một mình đầy bể là x (giờ, x > 24/5)
Khi đó trong một giờ vòi một chảy được 1/x (phần bể)
Vòi hai chảy một mình đầy bể trong x + 4 (giờ) nên trong một giờ chảy được: 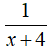
Tổng cộng trong một giờ hai vòi chảy được 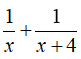
Sau 4 giờ 48 phút = 24/5 giờ hai vòi cùng chảy thì đầy bể nên trong một giờ chảy được 5/24 (phần bể) (4)
Từ (3) và (4) ta có phương trình
Vậy thời gian vòi một chảy một mình đầy bể là 8 giờ. Vòi hai chảy một mình đầy bể là 8 + 4 = 12 (giờ).
Câu 2: Một mảnh đất hình chữ nhật có độ dài đường chéo là 13m và chiều dài lớn hơn chiều rộng là 7m. Tính chiều dài và chiều rộng của mảnh đất đó.
Lời giải:
Gọi chiều rộng của mảnh đất hình chữ nhật là x (m, x > 0; x < 13)
Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)
Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:
x2 + (x + 7)2 = 132 ⇔ 2x2 + 14x - 120 = 0
Ta có:
Giải phương trình ta được x = 5 hoặc x = -12. Đối chiếu với điều kiện ta có chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.
III. Bài tập vận dụng
Câu 1: Một người dự định đi xe đạp từ địa điểm A tới địa điểm B cách nhau 36km trong một thời gian nhất định. Sau khi đi được nửa quãng đường, người đó dừng lại nghỉ 18 phút. Do đó để đến B đúng hạn, người đó đã tăng thêm vận tốc 2km trên quãng đường còn lại. Tính vận tốc ban đầu và thời gian thực tế xe lăn bánh trên đường.
Câu 2: Một ca nô đi xuôi dòng nước từ bến A đến bến B, cùng lúc đó một người đi bộ đi từ bến A dọc theo bờ sông về hướng B. Sau khi chạy được 24 km, ca nô quay trở lại và gặp người đi bộ tại địa điểm C cách bến A 18km. Tính vận tốc của ca nô khi nước yên lặng, biết vận tốc của người đi bộ và vận tốc dòng nước đều bằng 4km/h.
Xem thêm các bài Bài tập Toán lớp 9 hay, chi tiết khác:
Bài tập Ôn tập chương 4 Đại số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9