Nội dung bài viết

    Xem thêm

    Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo)

    Với giải bài tập Toán lớp 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo) chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.

    1 2,600 22/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo)

    Video giải Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo)

    Câu hỏi

    Câu hỏi 1 trang 13 Toán 8 Tập 1: Tính (a + b)(a + b)2 (với a, b là hai số tùy ý).

    Lời giải

    Ta có: (a + b)(a + b)2 = (a + b).(a2 + 2ab + b2)

    = a.(a2 + 2ab + b2) + b.(a2 + 2ab + b2)

    = a.a2 + a.2ab + a.b2 + b.a2 + b.2ab + b.b2

    = a3 + 2a2b + ab2 + ba2 + 2ab2 + b3

    = a3 + (2a2b + ba2) + (ab2 + 2ab2) + b3

    = a3 + 3a2b + 3ab2 + b3.

    Vậy (a + b)(a + b)2 = a3 + 3a2b + 3ab2 + b3.

    Câu hỏi 2 trang 13 Toán 8 Tập 1: Phát biểu hằng đẳng thức (4) bằng lời.

    Lời giải

    Lập phương của một tổng hai biểu thức bằng lập phương biểu thức thứ nhất cộng với ba lần tích của bình phương biểu thức thứ nhất với biểu thức thứ hai cộng với ba lần tích biểu thức thứ nhất với bình phương biểu thức thứ hai cộng với lập phương biểu thức thứ hai.

    Áp dụng trang 13 Toán 8 tập 1:

    a) Tính (x + 1)3.

    b) Tính (2x + y)3.

    Lời giải

    a) Ta có:

    (x + 1)3 = x3 + 3.x2.1 + 3.x.12 + 13

    = x3 + 3x2 + 3x + 1.

    Vậy (x + 1)3 = x3 + 3x2 + 3x + 1.

    b) Ta có:

    (2x + y)3 = (2x)3 + 3.(2x)2.y + 3.2x.y2 + y3

    = 8x3 + 3.4x2.y + 6xy2 + y3

    = 8x3 + 12x2y + 6xy2 + y3.

    Vậy (2x + y)3 = 8x3 + 12x2y + 6xy2 + y3.

    Câu hỏi 3 trang 13 Toán 8 Tập 1: Tính [a + (-b)]3 (với a, b là các số tùy ý).

    Lời giải

    Ta có:

    [a + (-b)]3 = a3 + 3a2.(-b) + 3a.(-b)2 + (-b)3

    = a3 – 3a2b + 3ab2 – b3.

    Vậy [a + (-b)]3 = a3 – 3a2b + 3ab2 – b3.

    Câu hỏi 4 trang 13 Toán 8 Tập 1: Phát biểu hằng đẳng thức số (5) bằng lời:

    Lời giải

    Lập phương của hiệu hai biểu thức bằng lập phương biểu thức thứ nhất trừ đi ba lần tích  bình phương biểu thức thứ nhất với biểu thức thứ hai cộng với ba lần tích của biểu thức thứ nhất với bình phương biểu thức thứ hai trừ đi lập phương biểu thức thứ hai.

    Áp dụng trang 13 và trang 14 Toán 8 Tập 1:

    a) Tính x−133.

    b) Tính (x – 2y)3.

    c) Trong các khẳng định sau, khẳng định nào đúng?

    1) (2x – 1)2 = (1 – 2x)2;

    2) (x – 1)3 = (1 – x)3;

    3) (x + 1)3 = (1 + x)3;

    4) x2 – 1 = 1 – x2;

    5) (x – 3)2 = x2 – 2x + 9;

    Em có nhận xét gì về mối quan hệ của (A – B)2 với (B – A)2 và (A – B)3 với (B – A)3.

    Lời giải

    a) Ta có:

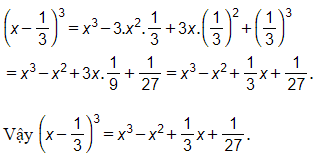
    Phát biểu hằng đẳng thức số (5) bằng lời (ảnh 1)

    b) Ta có: (x – 2y)3

    = x3 – 3.x2.(2y) + 3.x.(2y)2 + (2y)3

     = x3 – 6x2y + 3.x.4y2 + 8y3

    = x3 – 6x2y + 12xy2 + 8y3.

    Vậy (x – 2y)3 = x3 – 6x2y + 12xy2 - 8y3.

    c)

    1) Ta có: (2x – 1)2 = (2x)2 – 2.2x.1 + 12

    = 4x2 – 4x + 1.

    (1 – 2x)2 = 12 – 2.1.2x + (2x)2

    = 1 – 4x + 4x2 = 4x2 – 4x + 1.

    Suy ra (2x – 1)2 = (1 – 2x)2.

    Do đó phát biểu 1) đúng.

    2) Ta có: (x – 1)3 = x3 – 3.x2.1 + 3.x.12 – 13

    = x3 – 3x2 + 3x – 1.

    (1 – x)3 = 13 – 3.12.x + 3.1.x2 – x3

    = - x3 + 3x2 – 3x + 1.

    Suy ra (x – 1)3 ≠ (1 – x)3.

    Do đó phát biểu 2) sai.

    3) Ta có: (x + 1)3 = x3 + 3.x2.1 + 3.x.12 + 13

    = x3 + 3x2 + 3x + 1.

    (1 + x)3 = 13 + 3.12.x + 3.1.x2 + x3

    = x3 + 3x2 + 3x + 1.

    Suy ra (x + 1)3 = (1 + x)3.

    Do đó phát biểu 3) đúng.

    4) Ta có: x2 – 1 ≠ 1 – x2.

    Suy ra phát biểu 4) sai.

    5) Ta có: (x – 3)2 = x2 – 2x.3 + 32

    = x2 – 6x + 9 ≠ x2 – 2x + 9;

    Suy ra phát biểu 5) sai.

    Vậy có phát biểu 1) và 3) là phát biểu đúng.

    Nhận xét: Từ việc phân tích ví dụ c, ta có nhận xét sau:

    (A – B)2 = (B – A)2;

    (A – B)3 (B – A)3.

    Bài tập

    Bài 26 trang 14 Toán 8 Tập 1: Tính:

    a) (2x2 + 3y)3;

    b) 12x−33.

    Lời giải:

    a) Ta thấy rằng biểu thức này có dạng vế trái của hằng đẳng thức số (4) với A = 2x2, B = 3y.

    Áp dụng hằng đẳng thức số (4), ta có:

    (2x2 + 3y)3 = (2x2)3 + 3.(2x2)2.3y + 3.2x2.(3y)2 + (3y)3

    = 8x6 + 3.4x4.3y + 3.2x2.9y2 + 27y3

    = 8x6 + 36x4y + 54x2y2 + 27y3

    Vậy (2x2 + 3y)3 = 8x6 + 36x4y + 54x2y2 + 27y3.

    b) Ta thấy rằng biểu thức này có dạng vế trái của hằng đẳng thức số (5) với A=12x và B = 3.

    Áp dụng hằng đẳng thức số (5), ta có:

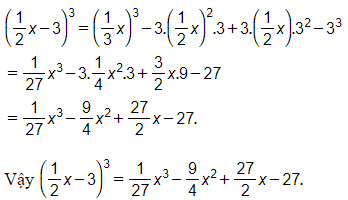
    Tính: (2x^2 + 3y)^3 (ảnh 1)

    Bài 27 trang 14 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:

    a) –x3 + 3x2 – 3x + 1

    b) 8 – 12x + 6x2 – x3

    Lời giải:

    a) –x3 + 3x2 – 3x + 1

    = (–x)3 + 3.(–x)2.1 + 3.(–x).1 + 13

    = (–x + 1)3 

    (Áp dụng HĐT (4) với A = –x và B = 1)

    b) 8 – 12x + 6x2 – x3

    = 23 – 3.22.x + 3.2.x2 – x3

    = (2 – x)3 

    (Áp dụng HĐT (5) với A = 2 và B = x)

    Bài 28 trang 14 Toán 8 Tập 1: Tính giá trị của biểu thức:

    a) x3 + 12x2 + 48x + 64 tại x = 6

    b) x3 – 6x2 + 12x – 8 tại x = 22

    Lời giải

    a) x3 + 12x2 + 48x + 64 = x3 + 3.x2.4 + 3.x.42 + 43 

    = (x + 4)3

    Tại x = 6, giá trị biểu thức bằng

    (6 + 4)3 = 103 = 1 000.

    b) x3 – 6x2 + 12x – 8 = x3 – 3.x2.2 + 3.x.22 – 23 

    = (x – 2)3

    Tại x = 22, giá trị biểu thức bằng

    (22 – 2)3 = 203 = 8000.

    Bài 29 trang 14 Toán 8 Tập 1: Đố. Đức tính đáng quý.

    Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tống hoặc một hiệu, rồi điền chữ dòng với biểu thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.

    x3 – 3x2 + 3x – 1

    16 + 8x + x2

    3x2 + 3x + 1 + x3

    1 – 2y + y2

    N

    U

    H

    Â

     

    (x – 1)3

    (x + 1)3

    (y – 1)2

    (x – 1)3

    (1 + x)3

    (1 – y)2

    (x + 4)2
                 

    Lời giải

    Ta có:

    N: x3 – 3x2 + 3x – 1

    = x3 – 3.x2.1 + 3.x.12 – 13 = (x – 1)3

    U: 16 + 8x + x2 = 42 + 2.4.x + x2 

    = (4 + x)2 = (x + 4)2

    H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1

    = (x + 1)3 = (1 + x)3

    Â: 1 – 2y + y2 = 12 – 2.1.y + y2 

    = (1 – y)2 = (y – 1)2

    Điền vào bảng như sau:

    (x – 1)3

    (x +1)3

    (y – 1)2

    (x – 1)3

    (1 + x)3

    (1 – y)2

    (x + 4)2

    N

    H

    Â

    N

    H

    Â

    U

    Vậy: Đức tính đáng quý là "NHÂN HẬU"

    Bài giảng Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo)

    Xem thêm lời giải bài tập Toán học lớp 8 hay, chi tiết khác:

    Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo)

    Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

    Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp sử dụng hằng đẳng thức

    Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử

    Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo)

    Trắc nghiệm Những hằng đẳng thức đáng nhớ (tiếp theo) có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,600 22/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: