Nội dung bài viết

    Xem thêm

    Toán 8 Bài 2: Hình thang

    Với giải bài tập Toán lớp 8 Bài 2: Hình thang chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.

    1 1,752 25/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 8 Bài 2: Hình thang

    Video giải Toán 8 Bài 2: Hình thang

    Câu hỏi

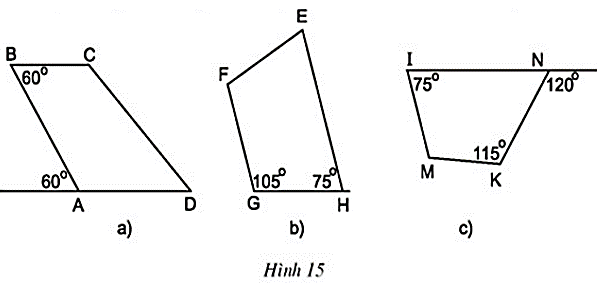
    Câu hỏi 1 trang 69 Toán 8 Tập 1: Cho hình 15.

    a) Tìm các tứ giác là hình thang.

    b) Có nhận xét gì về hai góc kề một cạnh bên của hình thang ?

    Tài liệu VietJack

    Lời giải

    a)

    +) Hình 15a)

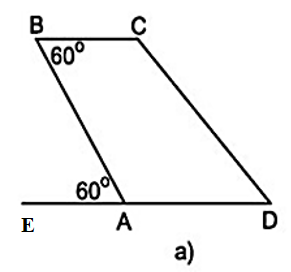
    Tài liệu VietJack

    Ta có: CBA^=BAE^=60°

    Mà hai góc ở vị trí so le trong

    ⇒BC∥AD

    Xét tứ giác ABCD có BC // AD

    ⇒Tứ giác ABCD là hình thang

    +) Hình 15b)

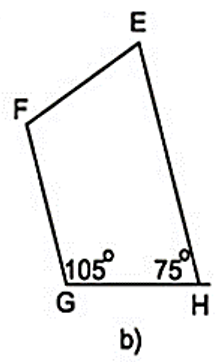
    Tài liệu VietJack

    Ta có: FGH^+EHG^=105°+75°=180°

    Mà hai góc ở vị trí trong cùng phía

    Suy ra: FG // EH

    Suy ra tứ giác EFGH là hình thang

    +) Hình 15c)

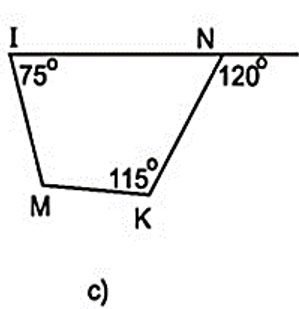
    Tài liệu VietJack

    Tứ giác IMKN không phải là hình thang.

    Vậy có tứ giác ABCD và tứ giác EFGH là hình thang.

    b) Do hình thang có hai cạnh đáy song song nên hai góc kề cạnh bên là hai góc ở vị trí trong cùng phía nên tổng hai góc này bằng 1800.

    Do đó ta rút ra nhận xét: Hai góc kề một cạnh bên của hình thang bù nhau.

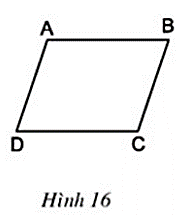
    Câu hỏi 2 trang 70 Toán 8 Tập 1: Hình thang ABCD có đáy AB, CD.

    a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.

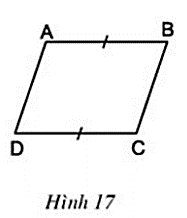
    b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.

    Tài liệu VietJackTài liệu VietJack

    Lời giải

    a)

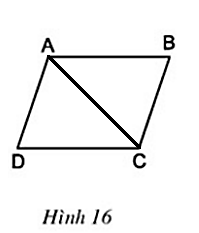
    Tài liệu VietJack

    Nối A với C

    Hình thang ABCD có đáy AB, CD

    ⇒ AB // CD

    ⇒BAC^=DCA^ (hai góc so le trong)

    Lại có: AD // BC

    ⇒DAC^=BCA^ (hai góc so le trong)

    Xét ΔABC và ΔCDA có:

    BAC^=DCA^ (cmt)

    AC chung

    DAC^=BCA^ (cmt)

    ⇒ ΔABC = ΔCDA (g.c.g)

    ⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)

    b)

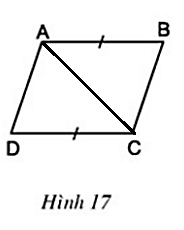
    Tài liệu VietJack

    Nối A với C

    Hình thang ABCD có đáy AB, CD

    ⇒ AB // CD

    ⇒BAC^=DCA^ (hai góc so le trong)

    Xét ΔABC và ΔCDA có:

    AC chung

    BAC^=DCA^ (cmt)

    AB = CD (gt)

    ⇒ ΔABC = ΔCDA (c.g.c)

    ⇒ AD = BC (hai cạnh tương ứng)

    ⇒ AD // BC (hai góc so le trong bằng nhau)

    Bài tập

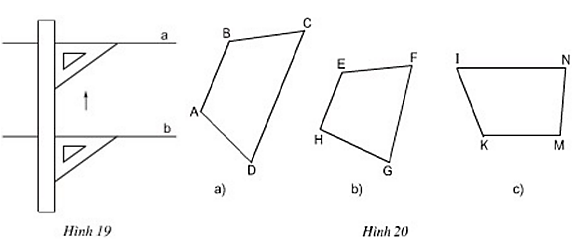
    Bài 6 trang 70 Toán 8 Tập 1: Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình 19). Trên hình 20, có những tứ giác là hình thang, có những tứ giác không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình 19, tứ giác nào là hình thang?

    Tài liệu VietJack

    Lời giải

    Đặt ê ke như hình vẽ để kiểm tra xem mỗi tứ giác có hay không hai cạnh song song.

    + Tứ giác ABCD có AB // CD nên là hình thang.

    + Tứ giác EFGH không có hai cạnh nào song song nên không phải hình thang.

    + Tứ giác KMNI có KM // IN nên là hình thang.

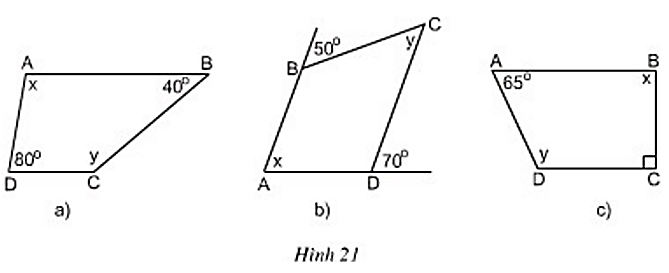
    Bài 7 trang 71 Toán 8 Tập 1: Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD.

    Tài liệu VietJack

    Lời giải

    Tứ giác ABCD là hình thang có đáy là AB và CD

    ⇒ AB // CD

    +) Hình 21a):

    Vì AB // CD ⇒A^+D^=180° (Hai góc trong cùng phía bù nhau)

    ⇒ x + 80º = 180º

    ⇒ x = 100º.

    Vì AB // CD

    ⇒B^+C^=180° (Hai góc trong cùng phía bù nhau)

    ⇒ 40º + y = 180º

    ⇒ y = 140º.

    Vậy x = 1000 và y = 1400.

    + Hình 21b):

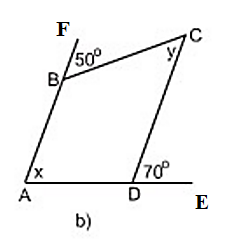
    Tài liệu VietJack

    Vì AB // CD

    ⇒A^=CDE^ (Hai góc đồng vị bằng nhau)

    ⇒ x = 70º

    Vì AB // CD

    ⇒DCB^=CBF^ (Hai góc so le trong bằng nhau)

    ⇒ y = 50º

    Vậy x = 700 và y = 500.

    +) Hình 21c):

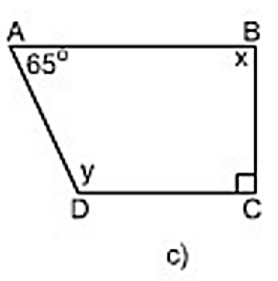
    Tài liệu VietJack

    Vì AB // CD ⇒ B^+C^=180° (Hai góc trong cùng phía bù nhau)

    hay x + 90º = 180º

    ⇒ x = 90º

    Vì AB // CD ⇒ A^+D^=180° (Hai góc trong cùng phía bù nhau)

    hay y + 65º = 180º

    ⇒ y = 115º.

    Vậy x = 900 và y = 1150.

    Bài 8 trang 71 Toán 8 Tập 1: Hình thang ABCD (AB // CD) có A^−D^=20°,B^=2C^.

    Tính các góc của hình thang.

    Lời giải

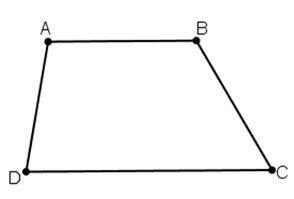
    Hình thang ABCD (AB // CD) có góc A - góc D = 20 độ (ảnh 1)

    Vì AB // CD ⇒A^+D^=180°(hai góc trong cùng phía)

    ⇒D^=180°−A^

    Thay D^=180°−A^ vào A^−D^=20°, ta được:

    A^−180°−A^=20°⇒A^−180°+A^=20°⇒2A^=20°+180°⇒2A^=200°⇒A^=200°:2=100°⇒D^=180°−100°=80°.

    Vì AB // CD ⇒B^+C^=180°(hai góc trong cùng phía)

    Thay B^=2C^ vào B^+C^=180°, ta được:

    2C^+C^=180°⇒3C^=180°⇒C^=180°:3=60°.⇒B^=2C^=2.60°=120°.

    Vậy A^=100°,D^=80°,C^=60°,B^=120°.

    Bài 9 trang 71 Toán 8 Tập 1: Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.

    Lời giải

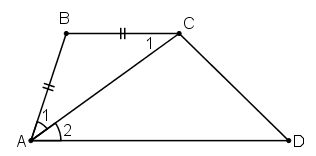
    Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A (ảnh 1)

    Để chứng minh tứ giác ABCD là hình thang ta chứng minh một cặp cạnh đối song song.

    Dựa vào hình vẽ, ta dự đoán: Phải chứng minh hai cạnh đối AD và BC song song.

    Để chứng minh một cặp cạnh song song thì sử dụng các cặp góc so le trong, đồng vị bằng nhau và cặp góc trong cùng phía bù nhau. Ở đây ta sẽ dùng cặp góc trong cùng phía, cụ thể là cặp góc C1^ và A2^

    Xét ΔABC có AB = BC

    ⇒ΔABC cân tại B

    ⇒A1^=C1^(hai góc ở đáy)

    Ta lại có: A1^=A2^(AC là phân giác của BAD^)

    ⇒A2^=C1^ (cùng bằng góc A1^)

    Mà hai góc này ở vị trí so le trong

    ⇒ AD // BC

    Vậy ABCD là hình thang (đpcm).

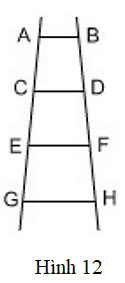
    Bài 10 trang 71 Toán 8 Tập 1: Đố. Hình 12 là hình vẽ một chiếc thang. Trên hình vẽ có bao nhiêu hình thang?

    Tài liệu VietJack

    Lời giải

    Có tất cả 6 hình thang, đó là:

    ABCD, CDFE, EFHG, ABFE, CDHG, ABHG

    Bài giảng Toán 8 Bài 2: Hình thang

    Xem thêm lời giải bài tập Toán học lớp 8 hay, chi tiết khác:

    Bài 3: Hình thang cân

    Bài 4: Đường trung bình của tam giác, của hình thang

    Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

    Bài 6: Đối xứng trục

    Bài 7: Hình bình hành

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Hình thang có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,752 25/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: