Nội dung bài viết

    Xem thêm

    Toán 8 Bài 1: Tứ giác

    Với giải bài tập Toán lớp 8 Bài 1: Tứ giác chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.

    1 2,742 25/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 8 Bài 1: Tứ giác

    Video giải Toán 8 Bài 1: Tứ giác

    Câu hỏi

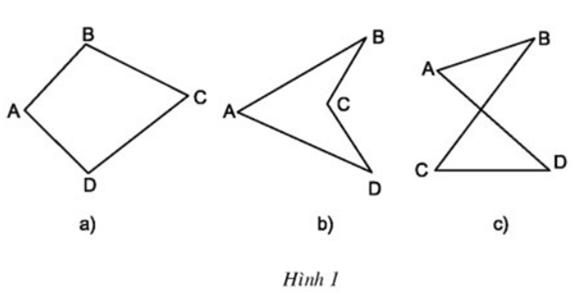
    Câu hỏi 1 trang 64 Toán 8 Tập 1: Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác?

    Tài liệu VietJack

    Lời giải

    Hình 1a) tứ giác ABCD luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

    Hình 1b) tứ giác ABCD nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

    Hình 1c) tứ giác ABCD nằm trên hai nửa mặt phẳng có bờ AD (hoặc bờ BC)

    Vậy chỉ có hình 1a) là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.

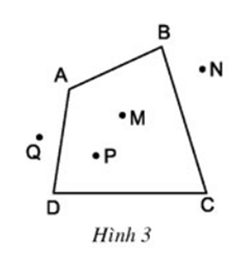
    Câu hỏi 2 trang 65 Toán 8 Tập 1: Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:

    Tài liệu VietJack

    a) Hai đỉnh kề nhau: A và B, …

    Hai đỉnh đối nhau: A và C, …

    b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …

    c) Hai cạnh kề nhau: AB và BC, …

    Hai cạnh đối nhau: AB và CD, …

    d) Góc: A^, …

    Hai góc đối nhau: A^ và C^, …

    e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …

    Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …

    Lời giải

    a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A

    Hai đỉnh đối nhau: A và C, B và D

    b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD

    c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB

    Hai cạnh đối nhau: AB và CD, AD và BC

    d) Góc: A^,B^,C^,D^.

    Hai góc đối nhau: A^ và C^, B^ và D^

    e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P

    Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q

    Câu hỏi 3 trang 65 Toán 8 Tập 1:

    a) Nhắc lại định lý về tổng ba góc của một tam giác

    b) Vẽ tứ giác ABCD tùy ý. Dựa vào định lý về tổng ba góc của một tam giác, hãy tính tổng A^+B^+C^+D^.

    Lời giải

    a) Trong một tam giác, tổng ba góc là 180o

    b)

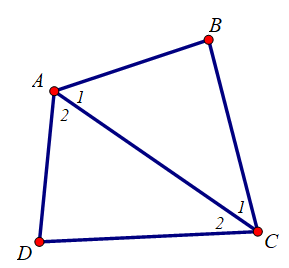
    Nhắc lại định lý về tổng ba góc của một tam giác (ảnh 1)

    Xét ΔABC có: A1^+B^+C1^=180°(Định lý tổng ba góc trong tam giác) (1)

    Xét ΔADC có: A2^+D^+C2^=180° (Định lý tổng ba góc trong tam giác) (2)

    Từ (1) và (2) suy ra: 

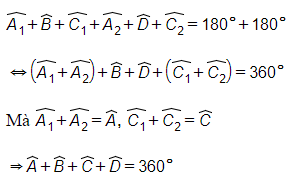
    Nhắc lại định lý về tổng ba góc của một tam giác (ảnh 1)

    Bài tập

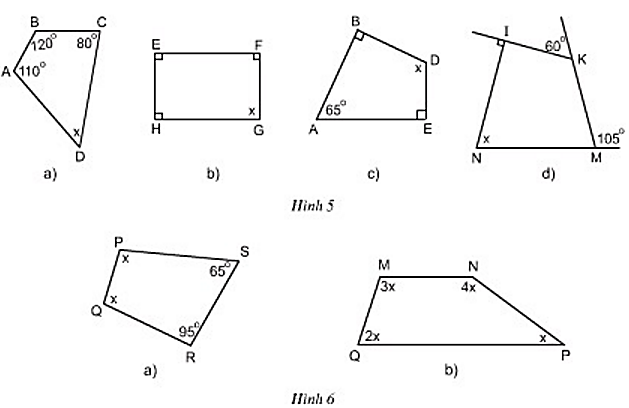
    Bài 1 trang 66 Toán 8 Tập 1: Tìm x ở hình 5, hình 6:

    Tài liệu VietJack

    Lời giải

    Ta có định lý: Tổng bốn góc trong một tứ giác bằng 360º.

    +) Hình 5a:

    Xét tứ giác ABCD, có:A^+B^+C^+D^=360°

    (Định lý tổng các góc của một tứ giác)

    ⇒ x + 110º + 120º + 80º = 360º

    ⇒ x = 360º – 110º – 120º – 80º

    ⇒ x = 50º.

    Vậy x = 50º.

    +) Hình 5b:

    Dựa vào hình vẽ ta có: E^=F^=H^=90°.

    Xét tứ giác EFGH ta có: 

    E^+F^+G^+H^=180° (Định lý tổng các góc của một tứ giác)

    ⇒ x + 90º + 90º + 90º = 360º

    ⇒ x = 360º – 90º – 90º – 90º = 90º.

    Vậy x = 90º.

    + Hình 5c:

    Dựa vào hình vẽ ta có: B^=E^=90°

    Xét tứ giác ABDE ta có:

    A^+B^+D^+E^=180°(Định lý tổng các góc của một tứ giác)

    ⇒ x + 90º + 65º + 90º = 360º

    ⇒ x = 360º – 90º – 65º – 90º = 115º

    Vậy x = 115º.

    + Hình 5d:

    kề bù với góc ⇒ IKM^=180°−60°=120°.

    KMN^ kề bù với góc ⇒KMN^=180°−105°=75°.

    NIK^ là góc vuông ⇒NIK^=90°

    Xét tứ giác IKMN, ta có:

    INM^+NMK^+MKI^+KIN^=360°(Định lý tổng bốn góc trong tứ giác)

    ⇒ x + 90º + 120º + 75º = 360º

    ⇒ x = 360º – 90º – 120º – 75º = 75º.

    Vậy x = 75º.

    + Hình 6a:

    Xét tứ giác PQRS, ta có:

    P^+Q^+S^+R^=180° (Định lý tổng bốn góc trong tứ giác)

    ⇒ x + x + 65º + 95º = 360º

    ⇒ 2x + 160º = 360º

    ⇒ 2x = 200º

    ⇒ x = 100º

    Vậy x = 100º.

    + Hình 6b:

    Xét tứ giác MNPQ ta có:

    M^+N^+P^+Q^=360° (Định lý tổng bốn góc trong tứ giác)

    ⇒ 3x + 4x + x + 2x = 360º

    ⇒ 10x = 360º

    ⇒ x = 36º.

    Vậy x = 36º.

    Bài 2 trang 66 Toán 8 Tập 1: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

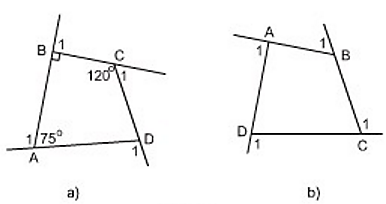
    a) Tính các góc ngoài của tứ giác ở hình 7a.

    b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): A1^+B1^+C1^+D1^=?

    c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

    Tài liệu VietJack

    Lời giải

    a) + Góc ngoài tại A là góc A1:

    A1^+BAD^=180°(hai góc kề bù)

    ⇒A1^+75°=180°⇒A1^=180°−75°⇒A1^=115°

    + Góc ngoài tại B là góc B1:

    B1^+ABC^=180°(hai góc kề bù)

    ⇒B1^+90°=180°⇒B1^=180°−90°⇒B1^=90°

    + Góc ngoài tại C là góc C1:

    C1^+BCD^=180°(hai góc kề bù)

    ⇒C1^+120°=180°⇒C1^=180°−120°⇒C1^=90°

    + Góc ngoài tại D là góc D1:

    Xét tứ giác ABCD, có:

    ABC^+BCD^+CDA^+DAB^=360° (Định lý tổng bốn góc trong một tứ giác)

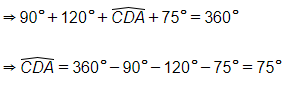
    Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác (ảnh 1)

    Ta có: CDA^+D1^=180° (hai góc kề bù)

    ⇒75°+D1^=180°⇒D1^=180°−75°=105°

    Vậy góc ngoài của tứ giác ABCD lần lượt là: A1^=115°, B1^=90°, C1^=90°, D1^=105°.

    b) Hình 7b:

    Ta có: A1^+BAD^=180° (hai góc kề bù)

    ⇒A1^=180°−BAD^

    B1^+ABC^=180° (hai góc kề bù)

    ⇒B1^=180°−ABC^

    C1^+BCD^=180°(hai góc kề bù)

    ⇒C1^=180°−BCD^

    D1^+CDA^=180°(hai góc kề bù)

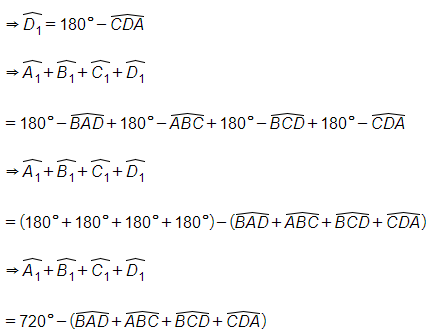
    Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác (ảnh 1)

    Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:

    BAD^+ABC^+BCD^+CDA^=360°⇒A1^+B1^+C1^+D1^=720°−360°=360°.

    c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.

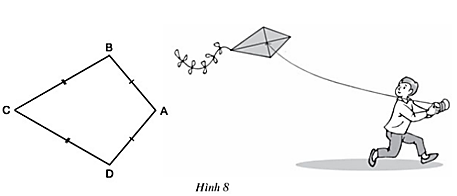
    Bài 3 trang 67 Toán 8 Tập 1: Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".

    a) Chứng minh rằng AC là đường trung trực của BD.

    b) Tính B^,D^ biết rằng A^=100°,C^=60°.

    Tài liệu VietJack

    Lời giải

    a) Ta có:

    AB = AD (gt) ⇒ A thuộc đường trung trực của BD

    CB = CD (gt) ⇒ C thuộc đường trung trực của BD

    Vậy AC là đường trung trực của BD

    b) Xét ΔABC và ΔADC có:

       AB = AD (gt)

       BC = DC (gt)

       AC cạnh chung

    ⇒ ΔABC = ΔADC (c.c.c)

    ⇒B^=D^ (2 góc tương ứng)

    Xét tứ giác ABCD, có: A^+B^+C^+D^=360° (định lý tổng bốn góc trong tứ giác)

    ⇒100°+B^+60°+D^=360°⇒B^+D^=360°−100°−60°⇒B^+D^=200°

    Mà B^=D^ (cmt)

    ⇒B^=D^=200°:2=100°

    Vậy B^=D^=100°.

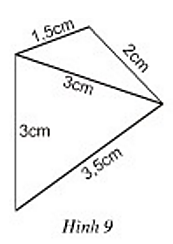
    Bài 4 trang 67 Toán 8 Tập 1: Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.

    Tài liệu VietJackTài liệu VietJack

    Lời giải

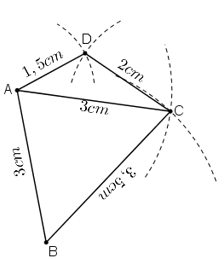
    - Cách vẽ hình 9:

    + Vẽ đoạn thẳng AB = 3cm

    + Quay cung tròn tâm A, bán kính 3cm, cung tròn tâm B bán kính 3,5cm. Hai cung tròn này cắt nhau tại C.

    + Quay cung tròn tâm C bán kính 2cm và cung tròn tâm A bán kính 1,5cm. Hai cung tròn này cắt nhau tại D.

    + Nối các đoạn BC, AC, CD, AD ta được hình cần vẽ.

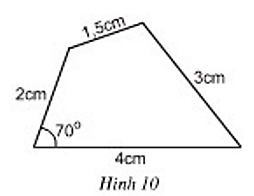
    Tài liệu VietJack

    - Cách vẽ hình 10:

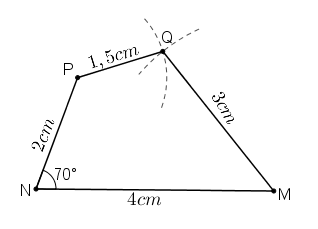
    + Vẽ đoạn thẳng MN = 4cm.

    + Dùng thước đo góc vẽ góc MNx^=70°. Trên tia Nx lấy điểm P sao cho NP = 2cm.

    + Vẽ cung tròn tâm P bán kính 1,5cm và cung tròn tâm M bán kính 3cm. Hai cung tròn này cắt nhau tại Q.

    + Nối PQ, MQ ta được hình cần vẽ.

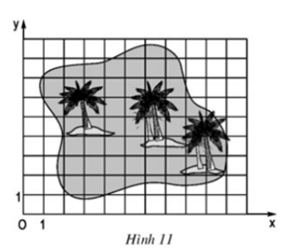
    Tài liệu VietJack

    Bài 5 trang 67 Toán 8 Tập 1: Đố. Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3;2), B(2;7), C(6;8), D(8;5).

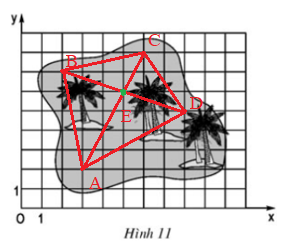
    Tài liệu VietJack

    Lời giải

    Tài liệu VietJack

    + Xác định các điểm A, B, C, D trong hệ trục tọa độ như trên hình vẽ.

    + Hai đường chéo của tứ giác là AC và BD.

    + Vị trí kho báu là giao điểm của AC và BD và là điểm E trên hình vẽ.

    + Nhìn trên hình vẽ thấy điểm E có tọa độ (5;6)

    Vậy vị trí tọa độ của kho báu là (5;6)

    Bài giảng Toán 8 Bài 1: Tứ giác

    Xem thêm lời giải bài tập Toán học lớp 8 hay, chi tiết khác:

    Bài 2: Hình thang

    Bài 3: Hình thang cân

    Bài 4: Đường trung bình của tam giác, của hình thang

    Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

    Bài 6: Đối xứng trục

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Tứ giác có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,742 25/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: