Nội dung bài viết

    Xem thêm

    Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước

    Với giải bài tập Toán lớp 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.

    1 1,365 26/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước

    Video giải Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước (P1)

    Video giải Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước (P2)

    Câu hỏi

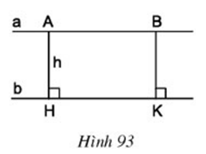
    Câu hỏi 1 trang 100 Toán 8 Tập 1: Cho hai đường thẳng song song a và b (h.93).

    Gọi A và B là hai điểm bất kì thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h.

    Tài liệu VietJack

    Lời giải

    Ta có: AH⊥bBK⊥b⇒AH//BK

    Vì a // b nên AB // HK

    ⇒ tứ giác ABKH là hình bình hành

    ⇒ AH = BK = h.

    Vậy BK = h.

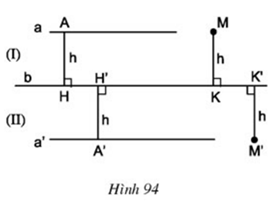
    Câu hỏi 2 trang 101 Toán 8 Tập 1: Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng M∈a,M'∈a'.

    Tài liệu VietJack

    Lời giải

    Xét tứ giác AMKH, có:

    AH⊥bMK⊥b⇒AH//MK

    AH = MK = h

    Suy tứ giác AMKH là hình bình hành

    ⇒AM // HK hay AM // b

    Mà đường thẳng a qua A cũng song song với b nên theo tiên đề Ơ – clit suy ra AM trùng đường thẳng a hay M thuộc a.

    Xét tứ giác A’M’K’H’, có:

    A'H'⊥bM'K'⊥b⇒A'H'//M'K'

    A’H’ = M’K’ = h

    Suy tứ giác A’M’K’H’ là hình bình hành

    ⇒A’M’ // H’K’ hay A’M’ // b

    Mà đường thẳng a’ qua A’ cũng song song với b nên theo tiên đề Ơ – clit suy ra A’M’ trùng đường thẳng a’ hay M’ thuộc a’.

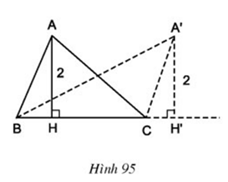
    Câu hỏi 3 trang 101 Toán 8 Tập 1: Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào?

    Tài liệu VietJack

    Lời giải

    Tam giác ABC có AH là đường cao và AH  = 2 cm nghĩa là điểm A cách đường thẳng BC một khoảng bằng 2.

    Tập hợp các điểm A cách đường thẳng BC một khoảng bằng 2 là đường thẳng song song với BC và cách BC một khoảng bằng 2cm.

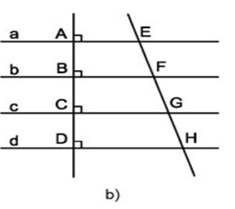
    Câu hỏi 4 trang 102 Toán 8 Tập 1: Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.

    Chứng minh rằng:

    a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.

    b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.

    Tài liệu VietJack

    Lời giải

    a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD

    ⇒ B là trung điểm của AC; C là trung điểm của BD

    Xét hình thang AEGC (AE // GC) có:

    B là trung điểm của AC  

    BF // AE // GC

    ⇒ F là trung điểm EG (định lí đường trung bình của hình thang)

    ⇒ EF = FG (1)

    Xét hình thang BFHD (BF // HD) có:

    C là trung điểm của BD 

    BF // GC // DH

    ⇒ G là trung điểm FH (định lí đường trung bình của hình thang)

    ⇒ GH = FG (2)

    Từ (1) và (2) suy ra EF = FG = GH.

    b) Ta có: EF = FG = GH

    ⇒ F là trung điểm của EG; G là trung điểm của FH

    Xét hình thang AEGC (AE // GC) có:

    F là trung điểm của EG

    BF // AE // GC

    ⇒ B là trung điểm AC (định lí đường trung bình của hình thang)

    ⇒ AB = BC (3)

    Xét hình thang BFHD (BF // HD) có:

    G là trung điểm của FH

    BF // GC // DH

    ⇒ C là trung điểm BD (định lí đường trung bình của hình thang)

    ⇒ BC = CD (4)

    Từ (3) và (4) suy ra AB = BC = CD.

    Vậy các đường thẳng a, b, c, d song song và cách đều nhau.

    Bài tập

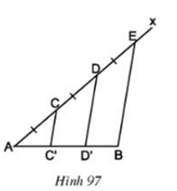
    Bài 67 trang 102 Toán 8 Tập 1: Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

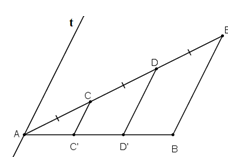
    Tài liệu VietJack

    Lời giải:

    Tài liệu VietJack

    Kẻ đường thẳng At // CC’ // DD’ // BE như hình vẽ.

    Ta có: AC = CD = DE

    ⇒ At, CC’, DD‘, BE là các đường thẳng song song cách đều

    ⇒ AC’ = C’D’ = D’B

    hay đoạn thẳng AB bị chia ra làm 3 phần bằng nhau.

    Bài 68 trang 102 Toán 8 Tập 1: Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?

    Lời giải

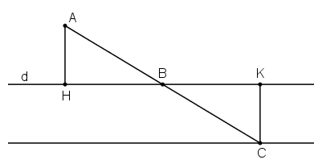
    Tài liệu VietJack

    Gọi H, K là hình chiếu của A và C trên đường thẳng d.

    ⇒ Khoảng cách từ A đến d bằng AH

    ⇒ AH = 2cm.

    Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:

    AHB^=CKB^=90°

    AB = BC (C đối xứng với A qua B)

    ABH^=CBK^ (2 góc đối đỉnh)

    ⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn)

    ⇒ CK = AH = 2cm (2 cạnh tương ứng).

    Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.

    Bài 69 trang 103 Toán 8 Tập 1: Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng:

    (1) Tập hợp các điểm cách A cố định một khoảng 3cm.

    (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định

    (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó

    (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm.

    (5) Là đường trung trực của đoạn thẳng AB.

    (6) là hai đường thẳng song song với a và cách a một khoảng 3cm.

    (7) là đường tròn tâm A bán kính 3cm.

    (8) là tia phân giác của góc xOy

    Lời giải

    Ghép các ý:

    (1) với (7)

    (2) với (5)

    (3) với (8)

    (4) với (6)

    Bài 70 trang 103 Toán 8 Tập 1: Cho góc vuông xOy, điểm A thuộc tia Oy sao cho OA = 2cm. Lấy B là một điểm bất kì thuộc tia Ox. Gọi C là trung điểm của AB. Khi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường nào?

    Lời giải

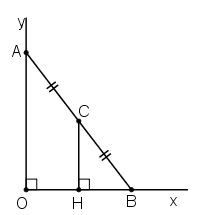
    Tài liệu VietJack

    - Cách 1:

    Kẻ CH ⊥ Ox

    Mà OA⊥Ox

    ⇒ CH // OA

    Xét tam giác AOB, ta có:

    CB = CA (gt) nên C là trung điểm AB

    CH // AO (cùng vuông góc Ox)

    ⇒ H là trung điểm của OB

    ⇒ HO = HB

    ⇒ CH là đường trung bình của tam giác AOB

    ⇒CH=AO2=22=1cm.

    Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên C di chuyển trên tia song song với Ox, cách Ox một khoảng bằng 1cm và nằm trong góc xOy.

    - Cách 2:

    Vì C là trung điểm của AB nên OC là trung tuyến ứng với cạnh huyền AB do đó OC = CA.

    Điểm C di chuyển trên đường trung trực của OA.

    Bài 71 trang 103 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.

    a) Chứng minh rằng ba điểm A, O, M thẳng hàng.

    b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?

    c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất?

    Lời giải:

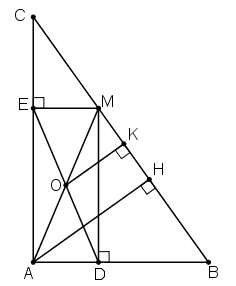
    Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì (ảnh 1)

    a) Tứ giác ADME có: EAD^=AEM^=ADM^=90°

    ⇒ ADME là hình chữ nhật

    O là trung điểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.

    Vậy A, O, M thẳng hàng.

    b) Kẻ AH ⊥ BC; OK ⊥ BC.

    Ta có OA = OM, OK // AH (cùng vuông góc BC)

    ⇒ MK = KH

    ⇒ OK là đường trung bình của ΔMAH

    ⇒OK=AH2

    ⇒ điểm O cách BC một khoảng cố định bằng AH2.

    ⇒ O nằm trên đường thẳng song song với BC các BC một khoảng bằng AH2.

    Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.

    Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.

    c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).

    Vậy AM nhỏ nhất khi M trùng H.

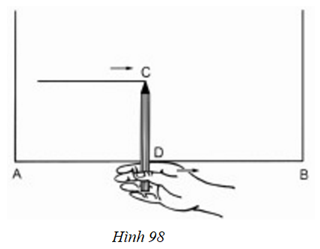
    Bài 72 trang 103 Toán 8 Tập 1: Đố. Để vạch một đường thẳng song song với mép gỗ AB và cách mép gỗ 10cm, bác thợ mộc đặt đoạn bút chì CD dài 10cm vuông góc với ngón tay trỏ lấy làm cữ (h.98), rồi đưa ngón trỏ chạy dọc theo mép gỗ AB. Căn cứ vào kiến thức nào mà ta kết luận rằng đầu chì C vạch nên đường thẳng song song với AB và cách AB là 10cm?

    Tài liệu VietJack

    Lời giải

    - Căn cứ vào tính chất đường thẳng song song với một đường thẳng cho trước.

    - Vì điểm C cách mép gỗ AB một khoảng không đổi bằng 10cm nên khi tay di chuyển thì đầu bút chì C vạch nên một đường thẳng song song với AB và cách AB một khoảng 10cm.

    Bài giảng Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước

    Xem thêm lời giải bài tập Toán học lớp 8 hay, chi tiết khác:

    Bài 11: Hình thoi

    Bài 12: Hình vuông

    Ôn tập chương 2

    Bài 1: Đa giác. Đa giác đều

    Bài 2: Diện tích hình chữ nhật

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,365 26/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: