Toán 8 Bài 3: Hình thang cân

Mục lục Giải Toán 8 Bài 3: Hình thang cân

Video giải Toán 8 Bài 3: Hình thang cân

Video giải Toán 8 Bài 3: Hình thang cân

Câu hỏi

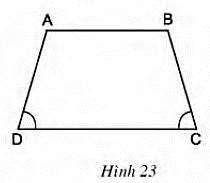
Câu hỏi 1 trang 72 Toán 8 Tập 1: Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt?

Lời giải

Hình thang ABCD trên hình 23 có hai góc kề cạnh đáy lớn bằng nhau

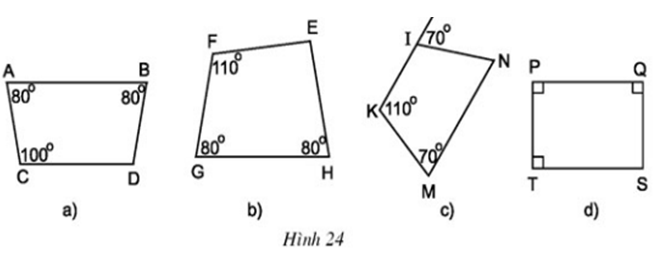
Câu hỏi 2 trang 72 Toán 8 Tập 1: Cho hình 24.

a) Tìm các hình thang cân.

b) Tính các góc còn lại của mỗi hình thang cân đó.

c) Có nhận xét gì về hai góc đối của hình thang cân ?

Lời giải

a)

+) Hình 24a) có: $\widehat{A}+\widehat{C}=80°+100°=180°$

Mà hai góc ở vị trí trong cùng phía nên AB//DC

Suy ra ABDC là hình thang.

Hình thang ABDC có $\widehat{A}=\widehat{B}=80°$

Suy ra ABDC là hình thang cân.

+) Hình 24b) tứ giác EFGH không là hình thang nên cũng không là hình thang cân.

+) Hình 24c) tứ giác MNIK có $\widehat{IKM}+\widehat{KMN}=110°+70°=180°$

Mà hai góc ở vị trí trong cùng phía nên MN // IK.

Suy ra MNIK là hình thang.

Ta có $\widehat{KIN}+70°=180°\Rightarrow \widehat{KIN}=180°-70°=110°$

$\Rightarrow \widehat{KIN}=\widehat{IKM}=110°.$

Suy ra MNIK là hình thang cân.

+) Hình 24d) tứ giác PQST có $\widehat{TPQ}+\widehat{PQS}=90°+90°=180°$

Mà hai góc ở vị trí trong cùng phía nên MN // IK.

Suy ra MNIK là hình thang.

Ta có $\widehat{KIN}+70°=180°$(hai góc kề bù)

$\Rightarrow \widehat{KIN}=180°-70°=110°$

$\Rightarrow \widehat{KIN}=\widehat{IKM}=110°.$

Suy ra MNIK là hình thang cân.

Các hình thang cân là : ABDC, IKMN, PQST

b)

Xét hình thang cân ABCD có AB // CD

$\Rightarrow \widehat{D}=\widehat{B}=100°$(hai góc kề một đáy bằng nhau)

Xét hình thang cân MNIK, có IK // MN:

$\Rightarrow \widehat{N}=\widehat{M}=70°$ (hai góc kề một đáy bằng nhau)

Xét hình thang cân PQST, có PQ // ST:

$\Rightarrow \widehat{S}=\widehat{T}=90°.$

c) Xét hình thang cân ABCD có:

$\widehat{A}+\widehat{C}=\widehat{B}+\widehat{D}=100°+80°=180°$

Xét hình thang cân MNIK có:

$\widehat{M}+\widehat{I}=\widehat{N}+\widehat{K}=110°+70°=180°$

Xét hình thang cân PQST có:

$\widehat{P}+\widehat{S}=\widehat{Q}+\widehat{T}=90°+90°=180°$

Nhận xét: Hai góc đối của hình thang cân bù nhau.

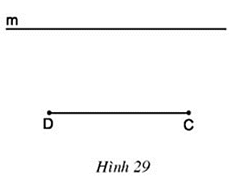
Câu hỏi 3 trang 74 Toán 8 Tập 1: Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc $\widehat{C}$ và $\widehat{D}$ của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.

Lời giải

Muốn xác định hai điểm A, B trên m ta lần lượt quay cung tròn tâm C bán kính R cắt đường thẳng m tại A và cung tròn tâm D bán kính R cắt đường thẳng m tại B.

Ta được hình thang ABCD.

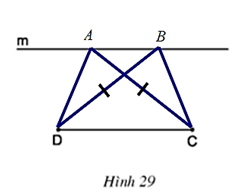
Sau khi tiến hàng đo, ta thấy hai góc C và D bằng nhau

Từ đó ta có dự đoán sau: Hình thang có hai đường chéo bằng nhau là hình thang cân.

Bài tập 

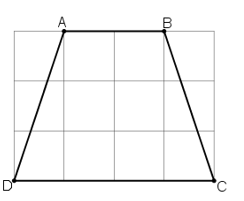
Bài 11 trang 74 Toán 8 Tập 1: Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).

Lời giải

(Mỗi ô vuông là 1cm).

Ta lấy điểm E như trên hình vẽ.

Quan sát vào hình vẽ ta thấy :

+ AB = 2cm

+ CD = 4cm.

+ Tính AD :

Xét tam giác vuông ADE có AE = 1cm, DE = 3cm:

AD² = AE² + DE² (Định lý Pytago)

AD² = 1² + 3² = 10

$\Rightarrow AD=\sqrt{10}cm.$

+ Tính BC :

ABCD là hình thang cân nên $AD=BC=\sqrt{10}cm$

Vậy các cạnh của hình thang lần lượt là: AB = 2cm, CD = 4cm, $AD=BC=\sqrt{10}cm$.

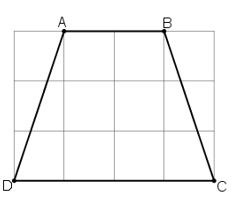
Bài 12 trang 74 Toán 8 Tập 1: Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.

Lời giải

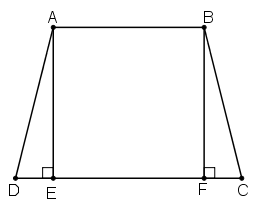
Vì hình thang ABCD cân nên ta có: AD = BC (hai cạnh bên bằng nhau)

Và $\widehat{C}=\widehat{D}$ (hai góc kề một đáy bằng nhau)

Xét $\Delta AED$ và $\Delta BFC$ có:

$\widehat{AED}=\widehat{BFC}=90°$

AD = BC (cmt)

$\widehat{C}=\widehat{D}$ (cmt)

⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)

⇒ DE = CF.

Bài 13 trang 74 Toán 8 Tập 1: Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.

Lời giải

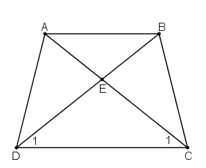
Do ABCD là hình thang cân nên:

AD = BC (hai cạnh bên bằng nhau)

AC = BD (hai đường chéo bằng nhau)

Xét $\Delta ADC$ và $\Delta BCD$, ta có:

AD = BC (cmt)

AC = BD (cmt)

DC cạnh chung

⇒ ΔADC = ΔBCD (c.c.c)

$\Rightarrow \widehat{C_1}=\widehat{D_1}$ (2 góc tương ứng)

⇒ ΔECD cân tại E

⇒ EC = ED.

Ta lại có:

AC – EC = EA

BD – ED = EB

Mà AC = BD và EC = ED

AC – EC = BD – ED hay EA = EB.

Vậy EA = EB, EC = ED.

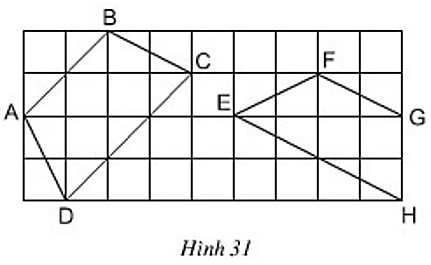
Bài 14 trang 75 Toán 8 Tập 1: Đố. Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?

Lời giải     

Ta quy ước mỗi ô vuông có cạnh 1cm.

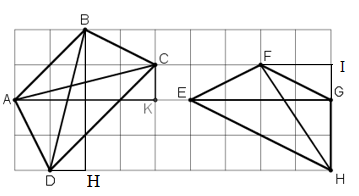
+ Xét tứ giác ABCD

Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.

Xét ΔACK vuông tại K, có AK = 4 cm, CK = 1cm:

AC² = AK² + KC² (định lý Py – ta – go)

AC² = 4² + 1² = 17

Xét ΔBHD vuông tại H, có BH = 4 cm, HD = 1cm:

BD² = BH² + HD² (định lý Py – ta – go)

BD² = 4² + 1² = 17

⇒ AC² = BD²

⇒ AC = BD

Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.

+ Xét tứ giác EFGH

FG // EH ⇒ Tứ giác EFGH là hình thang.

Lại có : EG = 4cm

Xét ΔFIH vuông tại I, có HI = 3 cm, IF = 2cm:

FH² = IH² + IF² (định lý Py – ta – go)

FH² = 3² + 2² = 13

$\begin{array}{l}\Rightarrow FH=\sqrt{13}cm.\\ \Rightarrow FH\ne EG\end{array}$

Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.

Bài 15 trang 75 Toán 8 Tập 1: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng góc $\widehat{A}=50°$.

Lời giải

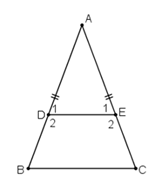
Xét tam giác ABC cân tại A có: $\widehat{B}=\widehat{C}=\frac{180°-\widehat{A}}{2}.$ (1)

Xét tam giác ADE có AD = AE nên tam giác ADE cân tại A

$\Rightarrow \widehat{ADE}=\widehat{AEC}=\frac{180°-\widehat{A}}{2}.$(2)

Từ (1) và (2) suy ra: $\widehat{ADE}=\widehat{B}$

Mà hai góc ở vị trí đồng vị nên DE // BC.

$\Rightarrow$DECB là hình thang

Mà $\widehat{B}=\widehat{C}$ là hai góc ở đáy

$\Rightarrow$DECB là hình thang cân.

b) Ta có: $\widehat{A}=50°$

$$\begin{gathered} \Rightarrow \widehat{B}=\widehat{C}=\frac{180°-\widehat{A}}{2} \\ =\frac{180°-50°}{2}=\frac{130°}{2}=65°. \end{gathered}$$

Vì DECB là hình thang cân có DE // BC

$\Rightarrow \widehat{BDE}+\widehat{B}=180°$(hai góc trong cùng phía bù nhau)

$\begin{array}{l}\Rightarrow \widehat{BDE}+65°=180°\\ \Rightarrow \widehat{BDE}=180°-65°=115°\end{array}$

Vì DECB là hình thang cân $\widehat{CED}=\widehat{BDE}=115°$(hai góc kề một đáy bằng nhau).

Vậy các góc của hình thang cân là: $\widehat{CED}=\widehat{BDE}=115°$ và $\widehat{B}=\widehat{C}=65°$.

Bài 16 trang 75 Toán 8 Tập 1: Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Lời giải

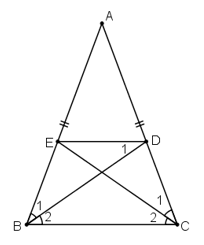
- Chứng minh tứ giác BCDE là hình thang cân:

Xét ΔABC cân tại A  $\Rightarrow \widehat{ABC}=\widehat{ACB}$ (hai góc ở đáy bằng nhau)

Ta có: $\widehat{B_1}=\widehat{B_2}=\frac{\widehat{ABC}}{2}$ (BD là phân giác $\widehat{ABC}$)

Ta có: $\widehat{C_1}=\widehat{C_2}=\frac{\widehat{ACB}}{2}$ (CE là phân giác $\widehat{ACB}$)

Mà $\widehat{ABC}=\widehat{ACB}$ (cmt)

$\Rightarrow \widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}.$

+ Xét ΔAEC và ΔADB có:

$\widehat{A}$ chung

AB = AC (gt)

$\widehat{B_1}=\widehat{C_1}$ (Cmt)

⇒ ΔAEC = ΔADB (g – c – g)

⇒ AE = AD (hai cạnh tương ứng)

Suy ra tam giác ADE cân tại A.

Xét tam giác ABC cân tại A có: $\widehat{B}=\widehat{C}=\frac{180°-\widehat{A}}{2}.$ (1)

Xét tam giác ADE có AD = AE nên tam giác ADE cân tại A

$\Rightarrow \widehat{ADE}=\widehat{AEC}=\frac{180°-\widehat{A}}{2}.$(2)

Từ (1) và (2) suy ra: $\widehat{ADE}=\widehat{B}$

Mà hai góc ở vị trí đồng vị nên DE // BC.

$\Rightarrow$DECB là hình thang

Mà $\widehat{B}=\widehat{C}$ là hai góc ở đáy

$\Rightarrow$DECB là hình thang cân.

- Chứng minh ED = EB.

Vì ED // BC  

$\Rightarrow \widehat{D_1}=\widehat{B_2}$(Hai góc so le trong)

Mà $\widehat{B_1}=\widehat{B_2}$

$\Rightarrow \widehat{D_1}=\widehat{B_1}$

⇒ ΔEDB cân tại E ⇒ ED = EB.

Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài 17 trang 75 Toán 8 Tập 1: Hình thang ABCD (AB // CD) có $\widehat{ACD}=\widehat{BDC}$. Chứng minh rằng ABCD là hình thang cân.

Lời giải

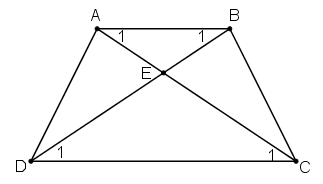
Gọi E là giao điểm của AC và BD.

Ta có: $\widehat{ACD}=\widehat{BDC}$

⇒ ΔEDC cân tại E ⇒ ED = EC (1)

Vì ABCD là hình thang có AB//CD:

$\Rightarrow \widehat{A_1}=\widehat{C_1}$ và $\widehat{B_1}=\widehat{D_1}$ (Các cặp góc so le trong)

Mà $\widehat{C_1}=\widehat{D_1}\Rightarrow \widehat{A_1}=\widehat{B_1}$

⇒ ΔEAB cân tại E ⇒ EA = EB (2)

Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.

Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.

Bài 18 trang 75 Toán 8 Tập 1: Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB//CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:

a) ΔBDE là tam giác cân.

b) ΔACD = ΔBDC

c) Hình thang ABCD là hình thang cân.

Lời giải

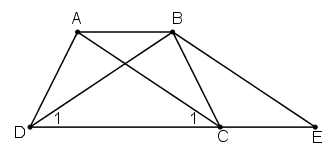
a)

Vì AB // CE $\Rightarrow \widehat{ABC}=\widehat{DCE}$ (hai góc so le trong)

Vì BE // AC $\Rightarrow \widehat{ACB}=\widehat{CBE}$ (hai góc so le trong)

Xét $\Delta ABC$ và $\Delta ECB$, có:

$\widehat{ABC}=\widehat{DCE}$ (cmt)

BC chung

$\widehat{ACB}=\widehat{CBE}$ (cmt)

$\Rightarrow \Delta ABC=\Delta ECB(g-c-g)$

$\Rightarrow$AC = BE (hai cạnh tương ứng)

Mà AC = BD nên BD = BE

Do đó tam giác BDE cân tại B.

b) Vì AC // BE nên $\widehat{E}=\widehat{C_1}$(hai góc đồng vị)

Tam giác BDE cân tại B $\Rightarrow \widehat{D_1}=\widehat{E}$ (hai góc ở đáy)

$\Rightarrow \widehat{C_1}=\widehat{D_1}\left(=\widehat{E}\right)$

Xét $\Delta ADC$ và $\Delta BCD$, có:

AC = BD (gt)

$\widehat{C_1}=\widehat{D_1}$(cmt)

CD chung

$\Rightarrow \Delta ADC=\Delta BCD\left(c-g-c\right)$

$\Rightarrow \widehat{ADC}=\widehat{BCD}$ (hai góc tương ứng)

Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

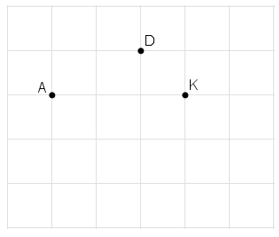
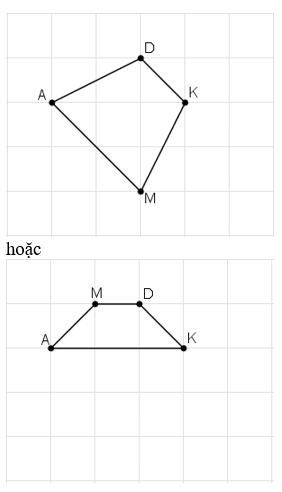
Bài 19 trang 75 Toán 8 Tập 1: Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M giao điểm của các dòng kẻ sao cho nó cùng với ba diểm đã cho là bốn đỉnh của một hình thang cân.

Lời giải

Ta có thể xác định hai điểm M thỏa mãn như dưới hình.

Bài giảng Toán 8 Bài 3: Hình thang cân

Xem thêm lời giải bài tập Toán học lớp 8 hay, chi tiết khác:

Bài 4: Đường trung bình của tam giác, của hình thang

Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

Bài 6: Đối xứng trục

Bài 7: Hình bình hành

Bài 8: Đối xứng tâm

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Hình thang cân có đáp án