Toán 8 Bài Ôn tập chương 2
Với giải bài tập Toán lớp 8 Bài Ôn tập chương 2 chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8.
Mục lục Giải Toán 8 Bài Ôn tập chương 2
Video giải Toán 8 Bài Ôn tập chương 2
Câu hỏi
Câu hỏi 1 trang 61 Toán 8 Tập 1: Định nghĩa phân thức đại số. Một đa thức có phải là một phân thức đại số không? Một số thực bất kì có phải là một phân thức đại số không ?
Lời giải
- Định nghĩa phân thức đại số:
Phân thức đại số (phân thức) là một biểu thức có dạng ABAB trong đó A, B là những đa thức và B là đa thức khác 0. A là tử thức, B là mẫu thức.
- Một đa thức được coi như một phân thức với mẫu thức bằng 1.
- Một số thực a bất kì cũng là một phân thức đại số vì chúng có thể viết được dưới dạng AB với A = a và B = 1.
Câu hỏi 2 trang 61 Toán 8 Tập 1: Định nghĩa hai phân thức đại số bằng nhau.
Lời giải
Hai phân thức AB và CD được gọi là bằng nhau nếu A.D = B.C.
Câu hỏi 3 trang 81 Toán 8 Tập 1: Phát biểu tính chất cơ bản của phân thức đại số.
Lời giải
Tính chất cơ bản của phân thức đại số:
- Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân thức mới bằng phân thức đã cho:
AB=A.MB.M (M là một đa thức khác 0)
Nếu chia cả tử và mẫu của một phân thức cho một nhân tử chung của chúng thì được một phân thức mới bằng phân thức đã cho:
AB=A.NB.N (N là một nhân tử chung của hai đa thức A và B)
Câu hỏi 4 trang 81 Toán 8 Tập 1: Nêu qui tắc rút gọn một phân thức đại số. Hãy rút gọn phân thức: 8x−48x3−1.
Lời giải
Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn:
8x−48x3−1=8x−4(2x)3−13=4(2x−1)(2x−1)(4x2−2x+1)=44x2−2x+1.
Câu hỏi 5 trang 81 Toán 8 Tập 1: Muốn qui đồng mẫu thức của nhiều phân thức có mẫu thức khác nhau làm thế nào?
Hãy qui đồng mẫu thức của hai phân thức: xx2+2x+1 và 35x2−5.
Lời giải
- Muốn qui đồng mẫu thức của nhiều phân thức ta có thể làm như sau:
+ Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung.
+ Tìm nhân tử phụ của mỗi mẫu thức.
+ Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
- Quy đồng mẫu hai phân thức trên:
Ta có: x2 + 2x + 1 = (x + 1)2 và 5x2 – 5 = 5(x2 – 1) = 5(x – 1)(x + 1)
MTC: 5(x – 1)(x + 1)2
Nhân tử phụ của phân thức thứ nhất là 5(x – 1):
xx2+2x+1=x(x+1)2=x.5(x−1)5(x−1)(x+1)2=5x2−5x5(x−1)(x+1)2.
Nhân tử phụ của phân thức thứ hai là x + 1:
35x2−5=35(x2−1)=35(x−1)(x+1)=3(x+1)5(x−1)(x+1)2=3x+35(x−1)(x+1)2.
Câu hỏi 6 trang 81 Toán 8 Tập 1: Phát biểu các qui tắc: Cộng hai phân thức cùng mẫu thức, cộng hai phân thức khác mẫu thức. Làm tính cộng: 3xx3−1+x−1x2+x+1.
Lời giải
- Qui tắc cộng hai phân thức cùng mẫu:
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức.
- Qui tắc cộng hai phân thức khác mẫu:
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
- Làm tính cộng:
3xx3−1+x−1x2+x+1=3x(x−1)(x2+x+1)+(x−1)2(x−1)(x2+x+1)=3x(x−1)(x2+x+1)+x2−2x+1(x−1)(x2+x+1)=3x+x2−2x+1(x−1)(x2+x+1)=x2+x+1(x−1)(x2+x+1)=1x−1.
Câu hỏi 7 trang 61 Toán 8 Tập 1: Hai phân thức như thế nào được gọi là hai phân thức đối nhau? Tìm phân thức đối của phân thức: x−15−2x.
Lời giải
- Hai phân thức được gọi là đối nhau nếu tổng của chúng bằng 0.
Phân thức đối của phân thức x−15−2x là phân thức −x−15−2x vì:
x−15−2x+(−x−15−2x)=x−15−2x+−x+15−2x=x−1−x+15−2x=0
Câu hỏi 8 trang 61 Toán 8 Tập 1: Phát biểu qui tắc trừ hai phân thức đại số.
Lời giải
Muốn trừ phân thức AB cho phân thức CD ta cộng phân thức AB cho phân thức đối của phân thức CD.
Câu hỏi 9 trang 81 Toán 8 Tập 1: Phát biểu qui tắc nhân hai phân thức đại số.
Lời giải
Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau.
Câu hỏi 10 trang 81 Toán 8 Tập 1: Cho phân thức: AB khác 0, viết phân thức nghịch đảo của nó.
Lời giải
Phân thức nghịch đảo của phân thức AB khác 0 là BA
Câu hỏi 11 trang 81 Toán 8 Tập 1: Phát biểu qui tắc chia hai phân thức đại số.
Lời giải
Muốn chia phân thức AB cho phân thức CD ta nhân phân thức AB với phân thức nghịch đảo của phân thức CD.
Câu hỏi 12 trang 81 Toán 8 Tập 1: Giả sử A(x)B(x) là một phân thức của biến x. Hãy nêu điều kiện của biến để giá trị của phân thức được xác định.
Lời giải
Phân thức được xác định khi biến x thỏa mãn B(x) ≠ 0.
Bài tập
Bài 57 trang 61 Toán 8 Tập 1: Chứng tỏ mỗi cặp phân thức sau bằng nhau:
Lời giải
a) Cách 1: Rút gọn biểu thức chưa tối giản:
Ta có: 3x+62x2+x−6=3(x+2)(2x−3)(x+2)=32x−3.
Vậy 32x−3=3x+62x2+x−6.
Cách 2: Quy đồng mẫu thức hai phân thức:
Ta có: 2x2 + x – 6 = (2x – 3)(x +2)
MTC: (2x – 3)(x +2)
Nhân tử phụ của phân thức thứ nhất là x + 2: 32x−3=3(x+2)(2x−3)(x+2)=3x+62x2+x−6.
Mẫu thức của phân thức thứ hai là MTC nên không phải quy đồng.
Vậy 32x−3=3x+62x2+x−6.
Cách 3: Sử dụng định nghĩa
Ta có:
3(2x2 + x – 6) = 3.2x2 + 3x – 3.6 = 6x2 + 3x – 18;
(2x – 3)(3x + 6) = 2x.3x + 2x.6 – 3.3x – 3.6
= 6x2 + 12x – 9x – 18 = 6x2 + 3x – 18.
Suy ra 3(2x2 + x – 6) = (2x – 3)(3x + 6).
Do đó 32x−3=3x+62x2+x−6.
Vậy 32x−3=3x+62x2+x−6.
b) 2x+4 và 2x2+6xx3+7x2+12x.
Cách 1: Rút gọn biểu thức chưa tối giản:
Ta có: 2x2+6xx3+7x2+12x=2x(x+3)x(x2+7x+12)
=2x(x+3)x(x+3)(x+4)=2x+4.
Vậy 2x+4=2x2+6xx3+7x2+12x.
Cách 2: Quy đồng mẫu thức hai phân thức:
Ta có:
x3 + 7x2 + 12x = x(x2 + 7x + 12) = x(x + 3)(x + 4).
MTC: x(x + 3)(x + 4).
Nhân tử phụ của phân thức thứ nhất là x(x + 3): 2x+4=2x(x+3)x(x+3)(x+4)=2x2+6xx3+7x2+12.
Mẫu thức của phân thức thứ hai là MTC nên không phải quy đồng.
Vậy 2x+4=2x2+6xx3+7x2+12x.
Cách 3: Sử dụng định nghĩa:
Ta có: 2(x3 + 7x2 + 12x) = 2x3 + 14x2 + 24x;
(x + 4)(2x2 + 6x) = x.2x2 + x.6x + 4.2x2 + 4.6x
= 2x3 + 6x2 + 8x2 + 24x = 2x3 + 14x2 + 24x;
Suy ra 2(x3 + 7x2 + 12x) = (x + 4)(2x2 + 6x).
Vậy 2x+4=2x2+6xx3+7x2+12x.
Bài 58 trang 62 Toán 8 Tập 1: Thực hiện các phép tính sau:
a)(2x+12x−1−2x−12x+1):4x10x−5;
c)1x−1−x3−xx2+1.(1x2−2x+1+11−x2).
Lời giải
a) (2x+12x−1−2x−12x+1):4x10x−5
=[(2x+1)2(2x−1)(2x+1)−(2x−1)2(2x−1)(2x+1)]:4x5(2x−1)=[(2x+1)2−(2x−1)2(2x−1)(2x+1)]:4x5(2x−1)=[(2x+1−2x+1)(2x+1+2x−1)(2x−1)(2x+1)]:4x5(2x−1)=[2.4x(2x−1)(2x+1)]:4x5(2x−1)=8x(2x−1)(2x+1).5(2x−1)4x=8x.5(2x−1)(2x−1)(2x+1).4x=102x+1.
b) (1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)−x(2−x)x(x+1)):(1x+x2x−2xx)=[1x(x+1)−2x−x2x(x+1)]:(x2−2x+1x)=[1−2x+x2x(x+1)]:(x2−2x+1x)=x2−2x+1x(x+1):x2−2x+1x=x2−2x+1x(x+1).xx2−2x+1=(x2−2x+1).xx(x+1).(x2−2x+1)=1x+1.
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
1x−1−x3−xx2+1.(1x2−2x+1−1x2−1)=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]=1x−1−x3−xx2+1.[x+1(x−1)2(x+1)−x−1(x−1)2(x+1)]=1x−1−x(x2−1)x2+1.[x+1−x+1(x−1)2(x+1)]=1x−1−x(x−1)(x+1)x2+1.2(x−1)2(x+1)=1x−1−2x(x2+1)(x−1)=x2+1(x−1)(x2+1)−2x(x2+1)(x−1)=x2+1−2x(x−1)(x2+1)=x2−2x+1(x−1)(x2+1)=(x−1)2(x−1)(x2+1)=x−1x2+1.
a) Cho biểu thức xPx+P−yPy−P. Thay P=xyx−y vào biểu thức đã cho rồi rút gọn biểu thức.
b) Cho biểu thức P2Q2P2−Q2. Thay P2Q2P2−Q2 và Q=2xyx2+y2 vào biểu thức đã cho rồi rút gọn biểu thức.
Lời giải
a) Thay P=xyx−y vào biểu thức ta được: x.xyx−yx+xyx−y−y.xyx−yy−xyx−y
Ta có:
x.xyx−yx+xyx−y−y.xyx−yy−xyx−y=x2yx−yx(x−y)x−y+xyx−y−xy2x−yy(x−y)x−y−xyx−y=x2yx−yx2−xy+xyx−y−xy2x−yxy−y2−xyx−y=x2yx−yx2x−y−xy2x−y−y2x−y=(x2yx−y:x2x−y)−(xy2x−y:−y2x−y)=(x2yx−y.x−yx2)−(xy2x−y.x−y−y2)=y−(−x)=y+x
b) Thay P=2xyx2−y2 và Q=2xyx2+y2 vào biểu thức trên ta được:
(2xyx2−y2)2.(2xyx2+y2)2(2xyx2−y2)2−(2xyx2+y2)2=(2xyx2−y2.2xyx2+y2)2(2xyx2−y2−2xyx2+y2)(2xyx2−y2+2xyx2+y2)=[2xy.2xy(x2−y2)(x2+y2)]2(2xyx2−y2−2xyx2+y2)(2xyx2−y2+2xyx2+y2)=[4x2y2x4−y4]2[2xy(x2+y2)−2xy(x2−y2)(x2−y2)(x2+y2)][2xy(x2+y2)+2xy(x2−y2)(x2−y2)(x2+y2)]=14x4y4(x4−y4)(2x3y+2xy3−2x3y+2xy3x4−y4)(2x3y+2xy3+2x3y−2xy3x4−y4)=16x4y4(x4−y4)(4xy3x4−y4)(4x3yx4−y4)=16x4y4(x4−y4)16x4y4(x4−y4)2=1
Bài 60 trang 62 Toán 8 Tập 1: Cho biểu thức: (x+12x−2+3x2−1−x+32x+2).4x2−45
a) Hãy tìm điều kiện của x để giá trị của biểu thức được xác định.
Lời giải
a) Cách 1: Biểu thức trên xác định khi tất cả các phân thức đều xác định
+ x+12x−2 xác định ⇔ 2x – 2 ≠ 0 ⇔ 2x ≠ 2 ⇔ x ≠ 1.
+ 3x2−1 xác định ⇔ x2 – 1 ≠ 0 ⇔ x2 ≠ 1 ⇔ x ≠ 1 và x ≠ -1.
+ x+32x+2 xác định ⇔ 2x + 2 ≠ 0 ⇔ 2x ≠ -2 ⇔ x ≠ -1
Vậy điều kiện xác định của biểu thức là x ≠ 1 và x ≠ -1.
Cách 2: Tìm mẫu chung: 2(x – 1)(x + 1)
Khi đó điều kiện của xác định của biểu thức là mẫu thức chung khác 0.
Suy ra: 2(x−1)(x+1)≠0⇔{x−1≠0x+1≠0⇔{x≠1x≠−1
Vậy điều kiện xác định của biểu thức là x ≠ 1 và x ≠ -1.
b) (x+12x−2+3x2−1−x+32x+2).4x2−45
=[(x+1).(x+1)2(x−1)(x+1)+3.22(x−1)(x+1)−(x+3)(x−1)2(x−1)(x+1)].4x2−45=[x2+2x+12(x−1)(x+1)+62(x−1)(x+1)−x2+2x−32(x−1)(x+1)].4(x−1)(x+1)5=[x2+2x+1+6−x2−2x+32(x−1)(x+1)].4(x−1)(x+1)5=102(x−1)(x+1).4(x−1)(x+1)5=10.4(x−1)(x+1)2.5(x−1)(x+1)=4
Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến.
Bài 61 trang 62 Toán 8 Tập 1: Tìm điều kiện của x để giá trị của biểu thức
(5x+2x2−10x+5x−2x2+10x).x2−100x2+4 được xác định. Tính giá trị của biểu thức tại x = 20 040.
Lời giải
+ Tìm điều kiện xác định:
Biểu thức xác định khi tất cả các phân thức đều xác định.
5x+2x2−10x xác định ⇔ x2 – 10x ≠ 0
⇔ x(x – 10) ≠ 0
⇔ x ≠ 0 và x – 10 ≠ 0
⇔ x ≠ 0 và x ≠ 10
5x−2x2+10x xác định ⇔ x2 + 10x ≠ 0
⇔ x(x + 10) ≠ 0
⇔ x ≠ 0 và x + 10 ≠ 0
⇔ x ≠ 0 và x ≠ -10
x2−100x2+4 luôn xác định vì x2 + 4 > 0 với mọi x∈ℝ.
Vậy điều kiện xác định của biểu thức là x ≠ 0, x ≠ 10 và x ≠ - 10.
+ Rút gọn biểu thức:
(5x+2x2−10x+5x−2x2+10x).x2−100x2+4=[(5x+2)(x+10)x(x−10)(x+10)+(5x−2)(x−10)x(x−10)(x+10)].x2−102x2+4=[5x2+52x+20x(x−10)(x+10)+5x2−52x+20x(x−10)(x+10)].(x−10)(x+10)x2+4=10x2+40x(x−10)(x+10).(x−10)(x+10)x2+4=10(x2+4)(x−10)(x+10)x(x−10)(x+10)(x2+4)=10x.
Thay x = 20040 vào biểu thức rút gọn, ta được: 1020 040=12 004.
Bài 62 trang 62 Toán 8 Tập 1: Tìm giá trị của x để biết giá trị của phân thức x2−10x+25x2−5x bằng 0.
Lời giải
+ Điều kiện xác định:
x2 – 5x ≠ 0 ⇔ x(x – 5) ≠ 0 ⇔ x ≠ 0 và x ≠ 5.
+ Ta có:
x2−10x+25x2−5x=0
⇒ x2 – 10x + 25 = 0
⇔ (x – 5)2 = 0
⇔ x – 5 = 0
⇔ x = 5 (Không thỏa mãn điều kiện xác định).
Vậy không có giá trị nào của x để giá trị phân thức trên bằng 0.
Bài 63 trang 62 Toán 8 Tập 1: Viết mỗi phân thức sau dưới dạng tổng của một đa thức và một phân thức với tử thức là một hằng số, rồi tìm các giá trị nguyên của x để giá trị của phân thức cũng là số nguyên:
Lời giải
a)3x2−4x−17x+2
=3x2+6x−10x−17x+2
(Tách -4x = 6x – 10x để nhóm với 3x2 xuất hiện x + 2)
=3x2+6x−10x−20+3x+2=3x(x+2)−10(x+2)+3x+2=3x(x+2)x+2−10(x+2)x+2+3x+2=3x−10+3x+2
Vì x∈ℤ để 3x−10+3x+2∈ℤ ⇔ x + 2 ∈ Ư(3) = {1; -1; 3; -3}
+ x + 2 = 1 ⇔ x = -1
+ x + 2 = -1 ⇔ x = -3
+ x + 2 = 3 ⇔ x = 1
+ x + 2 = -3 ⇔ x = -5
Vậy với x = 1; x = -1; x = -3 hoặc x = -5 thì phân thức có giá trị nguyên.
b) x2−x+2x−3
Có thể thực hiện phân tích tử thức như ý a) hoặc làm theo cách dưới đây:
Thực hiện chia x2 – x + 2 cho x – 3, ta được:
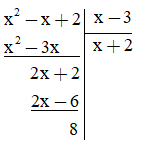
Khi đó ta có x2 – x + 2 = (x – 3)(x + 2) + 8
⇒x2−x+2x−3=(x−3)(x+2)+8x−3=(x−3)(x+2)x−3+8x−3=x+2+8x−3
Vì x∈ℤ nên để x2−x+2x−3∈ℤ thì 8x−3∈ℤ⇒ x – 3 ∈ Ư(8) = {-1; 1; 2; -2; 4; -4; 8; -8}.
+ x – 3 = 1 ⇔ x = 4
+ x – 3 = -1 ⇔ x = 2
+ x – 3 = 2 ⇔ x = 5
+ x – 3 = -2 ⇔ x = 1
+ x – 3 = 4 ⇔ x = 7
+ x – 3 = -4 ⇔ x = -1
+ x – 3 = 8 ⇔ x = 11
+ x – 3 = -8 ⇔ x = -5.
Vậy với x ∈ {-5; -1; 1; 2; 4; 5; 7; 11} thì giá trị phân thức là số nguyên.
Bài 64 trang 62 Toán 8 Tập 1: Tính giá trị của phân thức trong bài tập 62 tại x = 1,12 và làm tròn kết quả đến chữ số thập phân thức ba.
Lời giải
Điều kiện xác định: x ≠ 0 và x ≠ 5.
x2−10x+25x2−5x=x2−2.x.5+52x(x−5)=(x−5)2x(x−5)=x−5x.
Thay x = 1,12 vào biểu thức đa rút gọn, ta được:
1,12−51,12≈−3,464.
Xem thêm lời giải bài tập Toán học lớp 8 hay, chi tiết khác:
Bài 4: Đường trung bình của tam giác, của hình thang
Bài 5: Dựng hình bằng thước và compa. Dựng hình thang
Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
