Nội dung bài viết

    Xem thêm

    Giải Toán 8 trang 50 Kết nối tri thức

    Với giải bài tập Toán 8 trang 50 trong Bài 10: Tứ giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 trang 50.

    1 235 13/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 trang 50

    HĐ trang 50 Toán 8 Tập 1: Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng A^+B^+C^+D^ của tứ giác ABCD.

    HĐ trang 50 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

     

    Lời giải:

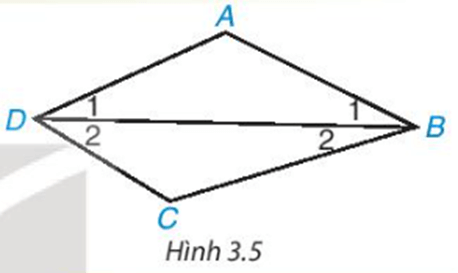
    Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:

    A^+B^1+D^1=180°;

    C^+B^2+D^2=180°.

    Khi đó, tứ giác ABCD có:

    A^+B^+C^+D^=A^+B^1+D^1+C^+B^2+D^2=180°+180°=360°.

    Vậy A^+B^+C^+D^=360° .

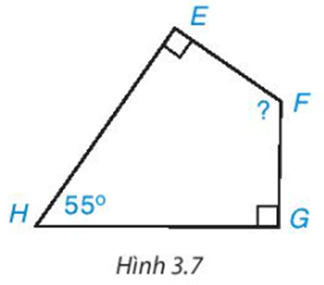
    Luyện tập 2 trang 50 Toán 8 Tập 1: Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F.

    Luyện tập 2 trang 50 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

     

    Lời giải:

    Xét tứ giác EFGH có:

    E^+F^+G^+H^=360° (định lí tổng các góc trong một tứ giác).

    Hay 90°+F^+90°+55°=360°

    Suy ra F^+235°=360°

    Do đó F^=360°−235°=125° .

    Vậy F^=125°.

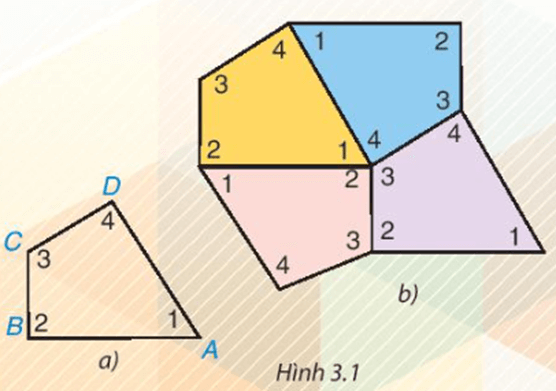
    Vận dụng trang 50 Toán 8 Tập 1: Giải bài toán mở đầu.

    Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.

    Vận dụng trang 50 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

    - Em có thể ghép bốn tứ giác khít nhau như vậy không?

    - Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

    Lời giải:

    - Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.

    Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.

    - Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.

    Khi đó: A^+B^+C^+D^=360° .

    Thử thách nhỏ trang 50 Toán 8 Tập 1: Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?

    Lời giải:

    • Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn 90o).

    Khi đó, tổng 4 góc nhỏ hơn: 4.90o = 360o (vô lí vì tổng 4 góc trong tứ giác bằng 360o).

    • Nếu tứ giác có 3 góc nhọn(nhỏ hơn 90o); 1 góc tù (góc lớn hơn 90o).

    Khi đó, tổng 3 góc nhọn nhỏ hơn: 3.90o = 270o;

    Số đo góc còn lại lớn hơn: 360o – 270o = 90o (thỏa mãn).

    Do đó,một tứ giác có thể có nhiều nhất 3 góc nhọn.

    • Nếu 4 góc tứ giác đều tù(mỗi góc lớn hơn 90o).

    Khi đó, tổng 4 góc lớn hơn: 4.90o = 360o (vô lí vì tổng 4 góc trong một tứ giác bằng 360o).

    • Nếu tứ giác có 3 góc tù và 1 góc nhọn.

    Tổng 3 góc tù lớn hơn: 3.90o = 270o;

    Số đo góc còn lại của tứ giác nhỏ hơn: 360o – 270o = 90o (thỏa mãn).

    Do đó,một tứ giác có thể có nhiều nhất 3 góc tù.

    Vậymột tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù.

    Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Giải Toán 8 trang 48

    Giải Toán 8 trang 49

    Giải Toán 8 trang 50

    Giải Toán 8 trang 51

    Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Mở đầu trang 48 Toán 8 Tập 1: Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a...

    Câu hỏi trang 49 Toán 8 Tập 1: Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho...

    Luyện tập 1 trang 49 Toán 8 Tập 1: Quan sát tứ giác ABCD trong Hình 3.4...

    HĐ trang 50 Toán 8 Tập 1: Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD...

    Luyện tập 2 trang 50 Toán 8 Tập 1: Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F...

    Vận dụng trang 50 Toán 8 Tập 1: Giải bài toán mở đầu. Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a...

    Thử thách nhỏ trang 50 Toán 8 Tập 1: Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao...

    Bài 3.1 trang 51 Toán 8 Tập 1: Tính góc chưa biết của các tứ giác trong Hình 3.8...

    Bài 3.2 trang 51 Toán 8 Tập 1: Tính góc chưa biết của tứ giác trong Hình 3.9. Biết rằng H^=E^+10° ...

    Bài 3.3 trang 51 Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”...

    Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài tập cuối chương 2

    Bài 11: Hình thang cân

    Luyện tập chung trang 56

    Bài 12: Hình bình hành

    Luyện tập chung trang 63

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 235 13/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: