Giải Toán 10 trang 45 Tập 2 Chân trời sáng tạo

Giải Toán 10 trang 45 Tập 2

Bài tập 2 trang 45 Toán lớp 10 Tập 2:  Chứng minh rằng:

a) $\overrightarrow{a}$  = (4; −6) và $\overrightarrow{b}$  = (−2; 3) là hai vectơ ngược hướng.

b) $\overrightarrow{a}$ = (−2; 3) và $\overrightarrow{b}$  = (−8; 12) là hai vectơ cùng hướng.

c)  $\overrightarrow{a}$ = (0; 4) và  $\overrightarrow{b}$ = (0; −4) là hai vectơ đối nhau.

Lời giải:

a) Ta có: (4; −6) = −2.(−2; 3) ⇒ $\overrightarrow{a}$   = −2 $\overrightarrow{b}$ ⇒  $\overrightarrow{a}$ và  $\overrightarrow{b}$ ngược hướng.

Vậy $\overrightarrow{a}$  = (4; −6) và  $\overrightarrow{b}$ = (−2; 3) là hai vectơ ngược hướng.

b) Ta có: (−8; 12) = 4(−2; 3) ⇒ $\overrightarrow{b}$ = 4$\overrightarrow{a}$

⇒ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.

Vậy $\overrightarrow{a}$ = (−2; 3) và  $\overrightarrow{b}$ = (−8; 12) là hai vectơ cùng hướng.

c) Ta có: (0; 4) = −1.(0; −4) ⇒ $\overrightarrow{a}$   = −$\overrightarrow{b}$

Mặt khác |$\overrightarrow{a}$ | = $\sqrt{0^2+4^2}$ = 4; | $\overrightarrow{b}$ | =  $\sqrt{0^2+{(-4)}^2}$ = 4.

Suy ra $\overrightarrow{a}$   = −$\overrightarrow{b}$  và |$\overrightarrow{a}$ | = | $\overrightarrow{b}$ | = 4. Do đó 2 vectơ đối nhau.

Vậy $\overrightarrow{a}$  = (0; 4) và $\overrightarrow{b}$  = (0; −4) là hai vectơ đối nhau.

Bài tập 3 trang 45 Toán lớp 10 Tập 2:  Tìm tọa độ các vectơ sau:

a) $\overrightarrow{a}$ = 2$\overrightarrow{i}$ +7$\overrightarrow{j}$ ;

b) $\overrightarrow{b}$ = − $\overrightarrow{i}$ + 3$\overrightarrow{j}$ ;

c) $\overrightarrow{c}$ = 4$\overrightarrow{i}$ ;

d) $\overrightarrow{d}$ = −9$\overrightarrow{j}$ .

Lời giải:

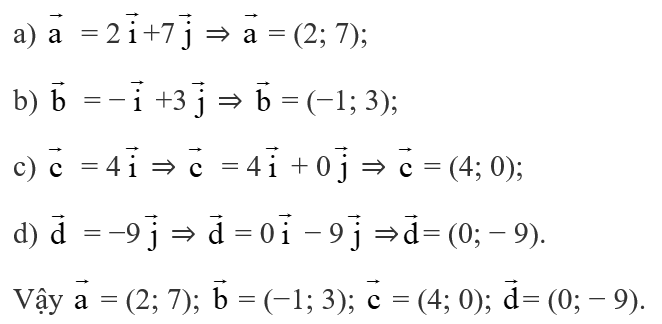
Bài tập 4 trang 45 Toán lớp 10 Tập 2:  Cho bốn điểm A(3; 5), B(4; 0), C(0; −3), D(2; 2). Trong các điểm đã cho, hãy tìm điểm:

a) Thuộc trục hoành;

b) Thuộc trục tung;

c) Thuộc đường phân giác của góc phần tư thứ nhất

Lời giải:

a) Điểm B(4; 0) có tung độ bằng 0 nên điểm B thuộc trục hoành.

b) Điểm C(0; −3) có hoành độ bằng 0 nên điểm C thuộc trục hoành.

c) Điểm D(2; 2) có hoành độ bằng tung độ nên điểm D thuộc đường phân giác của góc phần tư thứ nhất.

Vậy điểm B thuộc trục hoành, điểm C thuộc trục tung, điểm D thuộc đường phân giác của góc phần tư thứ nhất.

Bài tập 5 trang 45 Toán lớp 10 Tập 2:  Cho điểm M(x₀; y₀). Tìm tọa độ:

a) Điểm H là hình chiếu vuông góc của điểm M trên trục Ox;

b) Điểm M’ đối xứng với M qua trục Ox;

c) Điểm K là hình chiếu vuông góc của điểm M trên trục Oy;

d) Điểm M'' đối xứng với M qua trục Oy.

e) Điểm C đối xứng với điểm M qua gốc tọa độ.

Lời giải:

a)

a)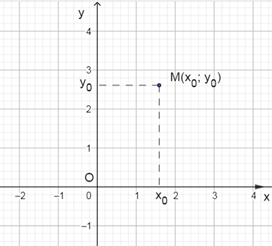

Do H là hình chiếu vuông góc của điểm M trên trục Ox nên điểm H có hoành độ bằng hoành độ của điểm M, và tung độ bằng 0.

⇒ H(x₀; 0).

Vậy điểm H là hình chiếu vuông góc của điểm M trên trục Ox thì H(x₀; 0).

b) M' đối xứng với M qua trục Ox ⇒ H là trung điểm của MM'

 $\left\{\begin{array}{l}{x}_H=\frac{x_M+x_{M\text{'}}}{2}\\ y_H=\frac{y_M+y_{M\text{'}}}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}{x}_0=\frac{x_0+x_{M\text{'}}}{2}\\ 0=\frac{y_0+y_{M\text{'}}}{2}\end{array}\right.$  ⇔ $\left\{\begin{array}{l}2x_0=x_0+x_{M\text{'}}\\ 0=y_0+y_{M\text{'}}\end{array}\right.$⇔ $\left\{\begin{array}{l}{x}_{M\text{'}}=x_0\\ y_{M\text{'}}=-y_0\end{array}\right.$

Vậy điểm M’ đối xứng với M qua trục Ox thì M’ có tọa độ là: M'(x₀; −y₀).

c) Do điểm K là hình chiếu vuông góc của điểm M trên trục Oy nên K có hoành độ bằng 0 và tung độ bằng tung độ của điểm M, tức là K(0; y₀)

Vậy điểm K là hình chiếu vuông góc của điểm M trên trục Oy thì K có tọa độ là: K(0; y₀).

d) M'' đối xứng với M qua trục Oy ⇒ K là trung điểm của MM''

 $\left\{\begin{array}{l}{x}_K=\frac{x_M+x_{M\text{'}\text{'}}}{2}\\ y_K=\frac{y_M+y_{M\text{'}\text{'}}}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}0=\frac{x_0+x_{M\text{'}\text{'}}}{2}\\ y_0=\frac{y_0+y_{M\text{'}\text{'}}}{2}\end{array}\right.$ ⇔ $\left\{\begin{array}{l}{x}_{M\text{'}\text{'}}=-x_0\\ y_{M\text{'}\text{'}}=y_0\end{array}\right.$

⇒ M''(−x₀; y₀).

Vậy điểm M'' đối xứng với M qua trục Oy thì M''(−x₀; y₀).

e) Vì C đối xứng với M qua gốc tọa độ O nên O là trung điểm của CM.

$\left\{\begin{array}{l}{x}_O=\frac{x_M+x_C}{2}\\ y_O=\frac{y_M+y_C}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}0=\frac{x_0+x_C}{2}\\ 0=\frac{y_0+y_C}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}{x}_C=-x_0\\ y_C=-y_0\end{array}\right.$

⇒ C(−x₀; −y₀).

Vậy điểm C đối xứng với điểm M qua gốc tọa độ thì C có tọa độ là: C(−x₀; −y₀).

Bài tập 6  trang 45 Toán lớp 10 Tập 2:  Cho ba điểm A(2; 2); B(3; 5), C(5; 5).

a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

b) Tìm tọa độ giao điểm hai đường chéo của hình bình hành.

c) Giải tam giác ABC.

Lời giải:

a) Xét D(x; y). Ta có: $\overrightarrow{AB}$ = (1; 3); $\overrightarrow{DC}$ = (5 − x; 5 − y)

ABCD là hình bình hành ⇔ $\overrightarrow{AB}$ = $\overrightarrow{DC}$

⇔ $\left\{\begin{array}{l}1=5-x\\ 3=5-y\end{array}\right.$ ⇔ $\left\{\begin{array}{l}x=4\\ y=2\end{array}\right.$

Vậy D(4; 2).

b) Gọi M là giao điểm hai đường chéo của hình bình hành ABCD.

Khi đó M là trung điểm của BD

⇒ $\left\{\begin{array}{l}{x}_M=\frac{3+4}{2}=\frac{7}{2}\\ y_M=\frac{5+2}{2}=\frac{7}{2}\end{array}\right.$ ⇒ $M\left(\frac{7}{2};\frac{7}{2}\right)$

Vậy $M\left(\frac{7}{2};\frac{7}{2}\right)$ .

Bài tập 7 trang 45 Toán lớp 10 Tập 2: Cho tam giác ABC có các điểm M(2; 2), N(3; 4), P(5; 3) lần lượt là trung điểm của các cạnh AB, BC và CA.

a) Tìm tọa độ các đỉnh của tam giác ABC.

b) Chứng minh rằng trọng tâm của tam giác ABC và MNP trùng nhau.

c) Giải tam giác ABC.

Lời giải:

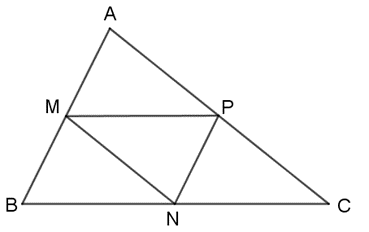
a) Ta có: $\overrightarrow{MP}$ = (3; 1); $\overrightarrow{BN}$ = (3 – x_B; 4 – y_B)

Có M là trung điểm cạnh AB, P là trung điểm cạnh AC nên MP là đường trung bình của tam giác ABC

⇒ MP // BC và MP = BN = $\frac{1}{2}$ BC ⇒ MPNB là hình bình hành.

Vậy A(4;1), B(0; 3), C(6; 5)

b) Gọi G là trọng tâm tam giác ABC, ta có: 

Vậy trọng tâm tam giác ABC trùng với trọng tâm tam giác MNP.

Bài tập 8 trang 45 Toán lớp 10 Tập 2:  Cho hai điểm A(1; 3), B(4; 2).

a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB

b) Tính chu vi tam giác OAB.

c) Chứng minh rằng OA vuông góc với AB và từ đó tính diện tích tam giác OAB.

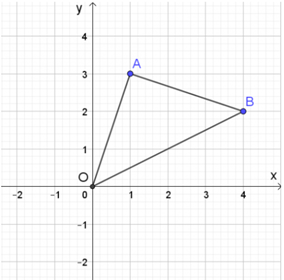
Lời giải: 

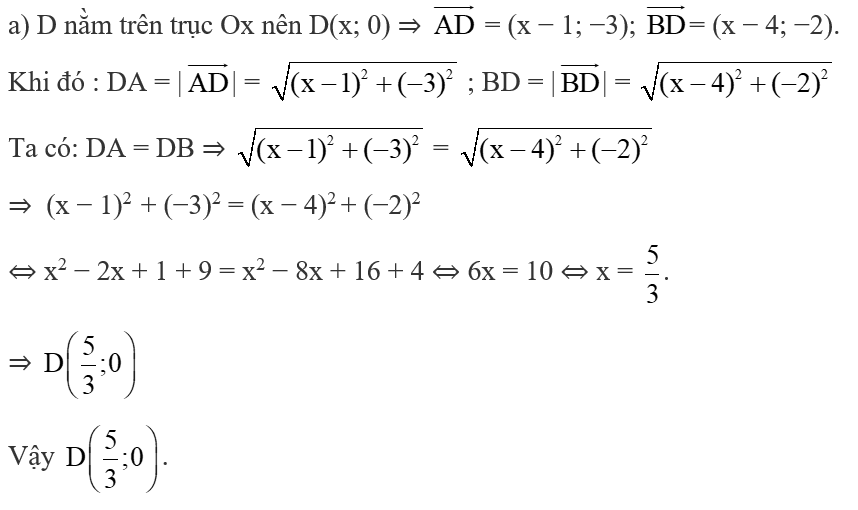
Bài tập 9 trang 45 Toán lớp 10 Tập 2:  Tính góc xen giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ trong các trường hợp sau:

a) $\overrightarrow{a}$ = (2; −3), $\overrightarrow{b}$ = (6; 4);

b) $\overrightarrow{a}$ = (3; 2); $\overrightarrow{b}$ = (5; −1);

c) $\overrightarrow{a}$ = (−2; $-2\sqrt{3}$ ), $\overrightarrow{b}$ = (3; $\sqrt{3}$ ).

Lời giải:

Bài tập 10 trang 45 Toán lớp 10 Tập 2:  Cho bốn điểm A(7; −3), B(8; 4), C(1; 5), D(0; −2). Chứng minh rằng tứ giác ABCD là hình vuông.

Lời giải:

Bài tập 11 trang 45 Toán lớp 10 Tập 2:  Một máy bay đang hạ cánh với vận tốc $\overrightarrow{v}$ = (−210; −42). Cho biết vận tốc của gió là $\overrightarrow{\text{w}}$ = (−12; −4) và một đơn vị trên hệ trục tọa độ tương ứng với 1 km. Tìm độ dài vectơ tổng hai vận tốc $\overrightarrow{v}$ và $\overrightarrow{\text{w}}$ .

Lời giải:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

Giải Toán 10 trang 38 Tập 2

Giải Toán 10 trang 39 Tập 2

Giải Toán 10 trang 40 Tập 2

Giải Toán 10 trang 41 Tập 2

Giải Toán 10 trang 42 Tập 2

Giải Toán 10 trang 43 Tập 2

Giải Toán 10 trang 44 Tập 2

Giải Toán 10 trang 45 Tập 2

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: 

Bài 2: Đường thẳng trong mặt phẳng tọa độ

Bài 3: Đường tròn trong mặt phẳng tọa độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố