Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Lấy điểm D trên cạnh BC sao cho BD = 2 cm

Lời giải Bài tập 13 trang 82 SBT Toán 8 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong sách bài tập Toán 8.

1 291 05/12/2023

Trang trước

Trang sau

Giải SBT Toán 8 (Kết nối tri thức) Bài tập ôn tập cuối năm

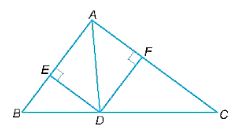
Bài tập 13 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Lấy điểm D trên cạnh BC sao cho BD = 2 cm. Lấy các điểm E, F trên các cạnh AB, AC sao cho DE, DF lần lượt vuông góc với AB, AC.

a) Chứng minh rằng ∆BDE ᔕ ∆DCF.

b) Tính độ dài đoạn thẳng AD.

Lời giải:

Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Lấy điểm

a) Xét tam giác ABC có:

AB² + AC² = BC² (do 3² + 4² = 5²).

Nên tam giác ABC vuông tại A (định lí Pythagore đảo).

Ta có DE, DF lần lượt vuông góc với AB, AC tại E và F.

Do đó, $\hat{D F C } = \hat{D F A} = \hat{D E A} = \hat{D E B} = 90 °$ .

Xét tứ giác AEDF có: $\hat{D F A} = \hat{D E A} = \hat{F A E} = 90 °$ .

Nên tứ giác AEDF là hình chữ nhật.

Do đó, $\hat{F D E} = 90 °$ .

Mà $\hat{C D F} + \hat{F D E} + \hat{E D B} = 180 °$ . Suy ra $\hat{C D F} + \hat{E D B} = 90 °$ .

Xét tam giác BDE và tam giác DCF có:

$\hat{D E B} = \hat{D F C} = 90 °$

$\hat{B} = \hat{F D C}$ $(= 90 ° - \hat{E D B})$

Do đó, ∆BDE ᔕ ∆DCF (g.g).

b) Tam giác ABC có: DE // AC (cùng vuông góc với AB).

Nên ∆BDE ᔕ ∆BCA.

Do đó, $\frac{E D}{A C} = \frac{E B}{A B} = \frac{B D}{B C}$ .

Suy ra $\frac{D E}{4} = \frac{E B}{3} = \frac{2}{5}$ .

Do đó, DE = $\frac{8}{5}$ cm, EB = $\frac{6}{5}$ cm.

Suy ra AE = AB – EB = 3 – $\frac{6}{5}$ $\frac{9}{5}$ cm.

Áp dụng định lí Pythagore vào tam giác AED vuông tại E có:

AD² = AE² + ED² = ${(\frac{9}{5})}^{2} + {(\frac{8}{5})}^{2} = \frac{29}{5}$ .

Suy ra $A D = \sqrt{\frac{29}{5}}$ cm.

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài tập 1 trang 81 SBT Toán lớp 8 Tập 2: Biết rằng hai đa thức A và B thỏa mãn các điều kiện sau:...

Bài tập 2 trang 81 SBT Toán lớp 8 Tập 2: Cho các đa thức:....

Bài tập 3 trang 81 SBT Toán lớp 8 Tập 2: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x....

Bài tập 4 trang 81 SBT Toán lớp 8 Tập 2: Phân tích các đa thức sau thành nhân tử:...

Bài tập 5 trang 81 SBT Toán lớp 8 Tập 2: Thực hiện các phép tính sau:....

Bài tập 6 trang 81 SBT Toán lớp 8 Tập 2: Cho phân thức đại số...

Bài tập 7 trang 81 SBT Toán lớp 8 Tập 2: Quãng đường AC gồm hai đoạn AB và BC. Đoạn BC dài hơn đoạn AB là 60 km...

Bài tập 8 trang 81 SBT Toán lớp 8 Tập 2: Cho hàm số y = (3m + 1)x – 2m....

Bài 9 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt...

Bài 10 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A, đường cao AH....

Bài tập 11 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC. Giả sử M là điểm trên cạnh AB...

Bài tập 12 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có đường cao AH....

Bài tập 13 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm...

Bài tập 14 trang 83 SBT Toán lớp 8 Tập 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy...

Bài tập 15 trang 83 SBT Toán lớp 8 Tập 2: Khảo sát trên 1 200 người trẻ tuổi ở Việt Nam...

Bài tập 16 trang 83 SBT Toán lớp 8 Tập 2: Một túi đựng 24 viên vi giống hệt nhau chỉ khác màu,...

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Chương 6: Phân thức đại số

Chương 7: Phương trình bậc nhất và hàm số bậc nhất

Chương 8: Mở đầu về tính xác suất của biến cố

Chương 9: Tam giác đồng dạng

Chương 10: Một số hình khối trong thực tiễn

1 291 05/12/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: