Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 8 Bài 39 (Kết nối tri thức): Hình chóp tứ giác đều

    Với giải sách bài tập Toán 8 Bài 39: Hình chóp tứ giác đều sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 39.

    1 543 05/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 39: Hình chóp tứ giác đều

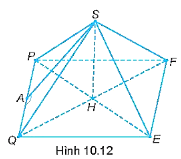
    Bài 10.8 trang 76 SBT Toán lớp 8 Tập 2: Hãy cho biết đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, một trung đoạn của hình chóp tứ giác đều S.PQEF trong Hình 10.12.

    Lời giải:

    Hãy cho biết đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, một trung đoạn của hình chóp

    Đỉnh: S.

    Các cạnh bên: SP, SQ, SE, SF.

    Các mặt bên: SPQ, SQE, SEF, SPF.

    Mặt đáy: PQEF.

    Đường cao: SH.

    Một trung đoạn: SA.

    Bài 10.9 trang 76 SBT Toán lớp 8 Tập 2: Kẻ bảng sau vào vở và điền vào ô còn trống.

    Đáy

    Mặt bên

    Số cạnh đáy

    Số cạnh bên

    Số mặt

    Hình chóp tam giác đều

    Tam giác đều

    Hình chóp tứ giác đều

    Tam giác cân

    Lời giải:

    Đáy

    Mặt bên

    Số cạnh đáy

    Số cạnh bên

    Số mặt

    Hình chóp tam giác đều

    Tam giác đều

    Tam giác cân

    3

    3

    4

    Hình chóp tứ giác đều

    Hình vuông

    Tam giác cân

    4

    4

    5

    Bài 10.10 trang 76 SBT Toán lớp 8 Tập 2: Cho hình chóp tứ giác đều S.HKIJ có cạnh bên SI = 10 cm, cạnh đáy HK = 8 cm. Hãy cho biết:

    a) Mặt bên và mặt đáy của hình chóp.

    b) Độ dài các cạnh bên và các cạnh đáy còn lại của hình chóp.

    Lời giải:

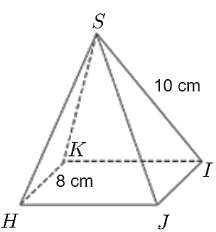
    Cho hình chóp tứ giác đều S.HKIJ có cạnh bên SI = 10 cm, cạnh đáy HK = 8 cm

    a) Các mặt bên của hình chóp: SHK, SHJ, SIJ, SKI.

    Mặt đáy của hình chóp: HKIJ.

    b) Các mặt bên của hình chóp tứ giác đều là các tam giác cân tại đỉnh nên các cạnh bên của hình chóp bằng nhau, do đó SK = SH = SJ = SI = 10 cm.

    Mặt đáy của hình chóp tứ giác đều là hình vuông nên KI = IJ = HJ = HK = 8 cm.

    Bài 10.11 trang 76 SBT Toán lớp 8 Tập 2: Cho hình chóp tứ giác đều D.ABCE có cạnh đáy bằng 6 cm, trung đoạn bằng 4 cm như Hình 10.13.

    a) Tính diện tích xung quanh của hình chóp.

    b) Tính diện tích toàn phần của hình chóp.

    Cho hình chóp tứ giác đều D.ABCE có cạnh đáy bằng 6 cm, trung đoạn bằng 4 cm

    Lời giải:

    a) Diện tích xung quanh của hình chóp tứ giác đều là:

    Sxq=p⋅d=12⋅4⋅6⋅4=48 (cm2).

    b) Diện tích mặt đáy là:

    Sđ = 62 = 36 (cm2).

    Bài 10.12 trang 77 SBT Toán lớp 8 Tập 2: Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều. Tính diện tích toàn phần của tứ giác đều tạo thành.

    Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều

    Lời giải:

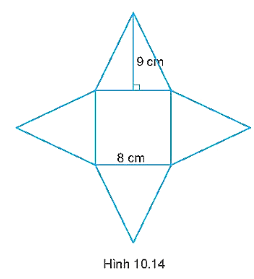
    Từ hình vẽ ta thấy hình chóp tứ giác đều được tạo thành cạnh đáy bằng 8 cm, trung đoạn bằng 9 cm.

    Diện tích xung quanh của hình chóp tứ giác đều là:

    Sxq=p⋅d=12⋅4⋅8⋅9=144(cm2).

    Diện tích mặt đáy là: Sđ = 82 = 64 (cm2).

    Diện tích toàn phần của hình chóp tứ giác đều là:

    Stp = Sxq + Sđ = 144 + 64 = 208 (cm2).

    Bài 10.13 trang 77 SBT Toán lớp 8 Tập 2: Bạn Thu dự định làm một chiếc đèn lồng có dạng là một hình chóp tứ giác đều cạnh đáy bằng 20 cm, chiều cao bằng 30 cm. Chiếc đèn lồng này có thể tích bằng bao nhiêu?

    Lời giải:

    Thể tích của chiếc đèn lồng là:

    V=13⋅S⋅h=13⋅202⋅30=4  000 (cm3).

    Bài 10.14 trang 77 SBT Toán lớp 8 Tập 2: Một hình chóp tứ giác đều có chiều cao bằng 12 cm, chu vi đáy bằng 32 cm. Thể tích của khối chóp này bằng bao nhiêu ?

    Lời giải:

    Mặt đáy của hình chóp tứ giác đều là hình vuông và có chu vi bằng 32 cm nên cạnh đáy của hình chóp tứ giác là: 32 : 4 = 8 (cm).

    Thể tích của hình chóp là:

    V=13S⋅h=13⋅82⋅12=256 (cm3).

    Diện tích toàn phần của hình chóp tứ giác đều là:

    Stp = Sđ + Sxq = 36 + 48 = 84 (cm2).

    Bài 10.15 trang 77 SBT Toán lớp 8 Tập 2: Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết 18,75≈4,3.

    Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15

    Lời giải:

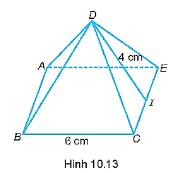
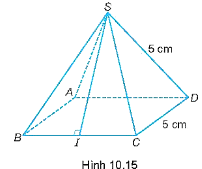
    Hình chóp tứ giác đều có mặt bên là các tam giác cân tại đỉnh và mặt đáy là hình vuông.

    Suy ra SC = SD = 5 cm; BC = CD = 5 cm.

    Tam giác SBC cân tại đỉnh S có SI là đường cao, đồng thời là trung tuyến hay I là trung điểm của BC, do đó IB = IC = BC2=52=2,5 (cm).

    Áp dụng định lý Pythagore vào tam giác SIC vuông tại I ta có:

    SI2 + IC2 = SC2

    Suy ra SI2 = SC2 – IC2 = 52 – (2,5)2 = 18,75.

    Do đó, SI = 18,75≈4,3 cm.

    Diện tích xung quanh của hình chóp là:

    Sxq=p⋅d≈12⋅4⋅5⋅4,3=43 (cm2).

    Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

    Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

    Bài 37: Hình đồng dạng

    Bài tập cuối chương 9

    Bài 38: Hình chóp tam giác đều

    Bài tập cuối chương 10

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 543 05/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: