Sách bài tập Toán 8 Bài 12 (Kết nối tri thức): Hình bình hành

Giải SBT Toán 8 Bài 12: Hình bình hành

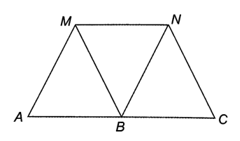
Bài 3.12 trang 37 SBT Toán 8 Tập 1: Xét hai hình bình hành MNBA và MNCB.

a) Chứng minh A, B, C là ba điểm thẳng hàng;

b) Chứng minh B là trung điểm của AC;

c) Hỏi tam giác MAB thoả mãn điều kiện gì để MNCA là một hình thang cân?

d) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thoả mãn điều kiện gì để MNDA là một hình thang cân?

Lời giải:

a) Do MNBA và MNCB là hình bình hành

Suy ra AB // MN, BC // MN nên theo tiên đề Euclid, hai đường thẳng AB và BC trùng nhau

Vậy ba điểm A, B, C thẳng hàng.

b) Do MNBA và MNCB là hình bình hành

Suy ra AB = MN, BC = MN

Mà A, B, C thẳng hàng nên B là trung điểm của AC.

c) Do MNCB là hình bình hành nên NC // MB, từ đó $\widehat{NCB}=\widehat{MBA}$ (hai góc đồng vị). Điều kiện để hình thang MNCA là hình thang cân là $\widehat{MAB}=\widehat{NCB}$ tức là $\widehat{MAB}=\widehat{MBA}.$

Vậy điều kiện để MNCA là hình thang cân là tam giác MAB cân tại M.

d)

Do MNDC là hình bình hành nên ND // MC, từ đó $\widehat{NDC}=\widehat{MCA}$ (hai góc đồng vị). Điều kiện để hình thang MNDA là hình thang cân là $\widehat{NDC}=\widehat{MCA}$.

Vậy điều kiện để MNDA là hình thang cân là $\widehat{MCA}=\widehat{MAC}$ tức là tam giác MAC cân tại M.

Do MB là đường trung tuyến của tam giác MAC nên điều kiện để tam giác MAC cân tại M là MB vuông góc với AC.

Vậy điều kiện để hình thang MNDA là hình thang cân đó là tam giác MAB vuông tại B.

Bài 3.13 trang 37 SBT Toán 8 Tập 1: Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó.

Lời giải:

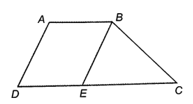
Xét hình thang ABCD với hai đáy AB và CD. Giả sử AB < CD.

Kẻ đường thẳng đi qua B song song với AD, cắt CD tại E.

Xét tứ giác ABED có: AB // DE và AD // BE

Do đó ABED là hình bình hành nên AB = DE và AD = BE.

Do AB < CD nên E nằm giữa C và D, do đó EC = DC – DE hay EC = DC ‒ AB. (1)

Trong tam giác BEC có: BE + BC > EC (bất đẳng thức trong tam giác)

Mà AD = BE nên AD + BC > EC (2)

Từ (1), (2) suy ra AD + BC > DC – AB.

Bài 3.14 trang 37 SBT Toán 8 Tập 1: Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều (Gợi ý: Chứng minh các tam giác AEF, DCF, BEC bằng nhau).

Lời giải:

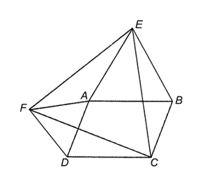
Do ABCD là hình bình hành nên AB // CD

Gọi $\widehat{BAD}=\alpha$

Vì AB // CD nên ta có $\widehat{BAD}+\widehat{ADC}=180°$

Suy ra $\widehat{ADC}=180°-\widehat{BAD}=180°-\alpha$

$\widehat{CDF}=\widehat{ADC}+\widehat{ADF}=180°-\alpha +60°=240°-\alpha$ (do ∆AFD nên $\widehat{ADF}=60°$) (1)

• Ta có: $\widehat{EAF}+\widehat{FAD}+\widehat{DAB}+\widehat{BAE}=360°$

Suy ra $\widehat{EAF}=360°-\widehat{FAD}-\widehat{DAB}-\widehat{BAE}$

Mà $\widehat{FAD}=\widehat{BAE}=60°$ (do ∆AFD và ∆ABE đều)

Suy ra $\widehat{EAF}=360°-60°-60°-\alpha =240°-\alpha \left(2\right)$

Từ (1) và (2) suy ra $\widehat{CDF}=\widehat{EAF}.$

Xét ∆AEF và ∆DCF có

AF = DF ( vì ∆ADF đều);

$\widehat{CDF}=\widehat{EAF}$ (chứng minh trên);

AE = DC (vì cùng bằng AB)

Do đó: ∆AEF =  ∆DCF (c.g.c)

Suy ra EF = CF (*)

• $\widehat{CBE}=\widehat{ABC}+\widehat{ABE}=\widehat{ABC}+60°$

Mà ABCD là hình bình hành nên $\widehat{ABC}=\widehat{ADC}=180°-\alpha$

Suy ra $\widehat{CBE}=180°-\alpha +60°=240°-\alpha$, mà $\widehat{CDF}=240°-\alpha$(chứng minh trên)

Suy ra $\widehat{CBE}=\widehat{CDF}.$

Xét ΔBCE và ΔDFC có:

BE = CD (vì cùng bằng AB);

$\widehat{CBE}=\widehat{CDF}$ (chứng minh trên);

BC = DF (vì cùng bằng AD)

Do đó ∆BCE = ∆DFC (c.g.c)

Suy ra CE = CF (**)

Từ (*) và (**) suy ra: EF = CF = CE

Vậy ∆ECF là tam giác đều.

Bài 3.15 trang 37 SBT Toán 8 Tập 1: Chứng minh rằng nếu hai góc kề của mỗi cạnh của một tứ giác đều là hai góc bù nhau thì tứ giác đó là một hình bình hành.

Lời giải:

Xét tứ giác ABCD có tính chất hai góc kề mỗi cạnh là hai góc bù nhau.

Vì $\widehat{A}+\widehat{B}=180°;\widehat{B}+\widehat{C}=180°$ nên $\widehat{A}=\widehat{C}$.

Vì $\widehat{B}+\widehat{C}=180°;\widehat{C}+\widehat{D}=180°$ nên $\widehat{B}=\widehat{D}$.

Vậy ABCD có mỗi cặp góc đối đều bằng nhau nên nó là một hình bình hành.

Bài 3.16 trang 37 SBT Toán 8 Tập 1: Cho hình thang ABCD với hai đáy AB, CD. Gọi K là trung điểm của BC. Lấy điểm A', D' sao cho K là trung điểm của AA' và DD'. Hỏi tứ giác AD'A'D là hình gì? Vì sao?

Lời giải:

Tứ giác AD'A'D có hai đường chéo AA', DD' cắt nhau tại trung điểm của mỗi đường nên là một hình bình hành.

Bài 3.17 trang 37 SBT Toán 8 Tập 1: Cho hai điểm phân biệt A, B nằm bên trong góc xOy (không bẹt). Tìm điểm D thuộc tia Ox, điểm E thuộc tia Oy sao cho ADBE là một hình bình hành.

Lời giải:

Gọi K là trung điểm của AB thì cần tìm D thuộc Ox, E thuộc Oy sao cho K là trung điểm của DE.

Lấy điểm M sao cho K là trung điểm của OM, kẻ các đường thẳng qua M song song với Ox, song song với Oy cắt Ox ở D, cắt Oy ở E cần tìm.

Thật vậy, nếu ME // OD và MD // OE thì ODME là hình bình hành

Mà K là trung điểm của OM nên K là trung điểm của DE

Lại có K là trung điểm của AB nên tứ giác ADBE có hai đường chéo DE, AB cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

Bài 3.18 trang 37 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho AE = CF; lấy các điểm G thuộc BC, H thuộc AD sao cho BG = DH. Chứng minh EGFH là một hình bình hành và các đường thẳng AC, BD, EF, GH đồng quy.

Lời giải:

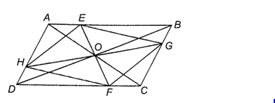
Do ABCD là hình bình hành nên $\widehat{BAD}=\widehat{BCD}$, AD = BC, AB = CD, $\widehat{ABC}=\widehat{ADC}$

• Ta có: AD = AH + DH, BC = BG + CG

Mà BG = DH, AD = BC nên AH = CG

Xét ∆AEH và ∆CFG có:

AH = CG, $\widehat{EAH}=\widehat{FCG}$(do $\widehat{BAD}=\widehat{BCD}$), AE = CF

Suy ra ∆AEH = ∆CFG (c.g.c) nên EH = FG.

Ta có: AB = AE + BE, CD = CF + DF

Mà AB = CD, AE = CF nên BE = DF

Xét ∆BEG và ∆DFH có:

BE = DF, $\widehat{EBG}=\widehat{HDF}$ (do $\widehat{ABC}=\widehat{ADC}$), BG = DH

Suy ra ∆BEG = ∆DFH (c.g.c) nên EG = FH.

Tứ giác EGFH có EH = FG, EG = FH nên là một hình bình hành.

• Do ABCD là hình bình hành nên khi ta gọi O là giao điểm của AC thì O là trung điểm của BD.

Vì tứ giác BEDF là hình bình hành (do EB = DF và EB // DF) nên hai đường chéo EF cắt nhau DB tại trung điểm O của BD.

Tương tự, GH đi qua trung điểm O của BD.

Vậy các đường thẳng AC, BD, EF, GH đồng quy.

Bài 3.19 trang 37 SBT Toán 8 Tập 1: Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.

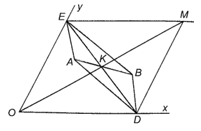
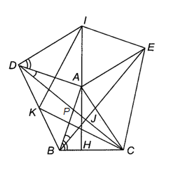
a) Chứng minh hai tam giác ABC và DAI bằng nhau.

b) Chứng minh đường thẳng AI vuông góc với BC.

c) Chứng minh đường thẳng BE vuông góc với đường thẳng CD.

d) Gọi K là trung điểm của BD, chứng minh KC = KI và KC vuông góc với KI. (Gợi ý: Chứng minh hai tam giác AKI và BKC bằng nhau).

Lời giải:

a) Hình bình hành AEID có $\widehat{ADI}+\widehat{DAE}=180°$(hai góc kề một cạnh của hình bình hành)

Ta có: $\widehat{DAE}+\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=360°$

Mà ∆ABD vuông tại A, ∆ACE vuông tại A, suy ra 

Suy ra $\widehat{BAC}+\widehat{DAE}=360°-90°-90°=180°$

Vậy $\widehat{ADI}=\widehat{BAC.}$

Do ∆ABD vuông cân tại A nên AD = AB

∆ACE vuông cân tại A nên AC = AE

Mà AEID là hình bình hành nên AE = DI, do đó DI = AC.

Xét ∆ADI và ∆BAC có

AD = AB, , DI = AC (chứng minh trên)

Suy ra ∆ADI = ∆BAC (c.g.c).

b) Giả sử AI cắt BC ở H .

Ta có: $\widehat{DAI}+\widehat{DAB}+\widehat{BAH}=180°$, mà $\widehat{DAB}=90°$(do ∆DAB vuông cân tại A)

Suy ra $\widehat{DAI}+\widehat{BAH}=90°$

Mà $\widehat{DAI}=\widehat{ABC}$(do ∆ADI = ∆BAC) nên $\widehat{ABH}+\widehat{BAH}=90°$

Trong ∆ABH có: $\widehat{ABH}+\widehat{BAH}+\widehat{AHB}=180°$

Suy ra $\widehat{AHB}=180°\left(\widehat{ABH}+\widehat{BAH}\right)=180°-90°=90°$ hay AI ⊥ BC.

c) Ta có $\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=\widehat{BAC}+90°$ và $\widehat{DAC}=\widehat{BAC}+\widehat{BAD}=\widehat{BAC}+90°$

Do đó $\widehat{BAE}=\widehat{DAC}$

Xét ∆BAE và ∆DAC có:

AB = AD; $\widehat{BAE}=\widehat{DAC}$; AC = AE

Do đó ∆BAE = ∆DAC (c.g.c)

Suy ra $\widehat{EBA}=\widehat{CDA}$

Gọi J là giao của DC và BE, ta có $\widehat{JBA}=\widehat{JDA}.$

Gọi P là giao điểm của AB và CD.

Tam giác ADP vuông tại A nên $\widehat{PDA}+\widehat{DPA}=90°$

Mà $\widehat{PDA}=\widehat{JBP}$ và $\widehat{DPA}=\widehat{BPJ}$ (đối đỉnh)

Do đó $\widehat{JBP}+\widehat{BPJ}=90°$, suy ra $\widehat{PJB}=90°$ hay CD vuông góc với BE.

d) Tam giác ABD vuông cân tại A nên AK vừa là đường trung tuyến, vừa là đường cao, đường phân giác. Do đó $\widehat{DAK}=\frac{1}{2}\widehat{BAD}=45°$

Khi đó $\widehat{ABK}=\widehat{BAK}=45°$ nên DABK vuông cân tại K, do đó KA = KB

Ta có: $\widehat{KAI}=\widehat{DAK}+\widehat{DAI}=45°+\widehat{DAI}=45°+\widehat{ABC}$

Mặt khác $\widehat{KBC}=\widehat{ABK}+\widehat{ABC}=45°+\widehat{ABC}$ (do DABD vuông cân tại A nên $\widehat{ABK}=45°)$

Do đó $\widehat{KAI}=\widehat{KBC}$.

Xét DAKI và ∆BKC có:

AK = BK, $\widehat{KAI}=\widehat{KBC}$, AI = BC (do ∆ADI = ∆BAC)

Suy ra ∆AKI = ∆BKC (c.g.c) nên KI = KC và 

Ta có: $\widehat{AKC}+\widehat{BKC}=90°$

Mà $\widehat{AKI}=\widehat{BKC}$ nên $\widehat{AKC}+\widehat{AKI}=90°$ hay $\widehat{IKC}=90°$ nên KI và KC vuông góc.

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác: 

Bài 11: Hình thang cân

Bài 13: Hình chữ nhật

Bài 14: Hình thoi và hình vuông

Bài tập cuối chương 3

Bài 15: Định lí Thalès trong tam giác