Sách bài tập Toán 8 (Kết nối tri thức) Bài tập cuối chương 7 trang 35

Giải SBT Toán 8 Bài tập cuối chương 7 trang 35

Câu 1 trang 35 SBT Toán 8 Tập 2: Phương trình nào sau đây là phương trình bậc nhất một ẩn ?

A. 0x + 1 = 0;

B. x – 1 = x + 2;

C. 3x² + 2 = 0;

D. –3x = 2.

Lời giải:

Đáp án đúng là: D

Đáp án A không phải phương trình bậc nhất một ẩn vì hệ số của x là 0.

Đáp án B không phải phương trình bậc nhất một ẩn vì:

x – 1 = x + 2

0 = 3

Đáp án C không phải phương trình bậc nhất một ẩn vì x có bậc là 2.

Đáp án D là phương trình bậc nhất một ẩn.

Câu 2 trang 35 SBT Toán 8 Tập 2: Tập nghiệm S của phương trình 3(x + 1) – (x – 2) = 7 – 2x là:

A. S = {0};

B. S = $\left\{\frac{1}{2}\right\}$;

C. S = ∅;

D. S = ℝ.

Lời giải:

Đáp án đúng là: B

Ta có:

3(x + 1) – (x – 2) = 7 – 2x

3x + 3 – x + 2 = 7 – 2x

3x – x + 2x = 7 – 3 – 2

4x = 2

x =$\frac{1}{2}$

Vậy tập nghiệm của phương trình là: S = $\left\{\frac{1}{2}\right\}$ .

Câu 3 trang 35 SBT Toán 8 Tập 2: Hàm số nào sau đây là hàm số bậc nhất ?

A. y = 0x + 3;

B. y = 2x² + 5;

C. y = –x;

D. y = 0.

Lời giải:

Đáp án đúng là: C

Hàm số y = 0x + 3 có hệ số của x là 0 nên không là hàm số bậc nhất.

Hàm số y = 2x² + 5 là không là hàm số bậc nhất vì bậc của x là 2.

Hàm số y = –x là hàm số bậc nhất.

Hàm số y = 0 là hàm số hằng.

Câu 4 trang 35 SBT Toán 8 Tập 2: Phương trình đường thẳng có hệ số góc –2 và đi qua điểm (1; 3) là

A. y = –2x + 3;

B. y = –2x + 1;

C. y = –2x + 4;

D. y = –2x + 5;

Lời giải:

Đáp án đúng là: D

Gọi phương trình đường thẳng cần tìm là: y = ax + b.

Phương trình đường thẳng có hệ số góc –2 nên a = –2.

Đường thẳng đi qua điểm (1; 3) nên ta có:

3 = –2 . 1 + b

3 = –2 + b

b = 5

Vậy phương trình đường thẳng cần tìm là: y = –2x + 5.

Câu 5 trang 35 SBT Toán 8 Tập 2: Hệ số góc của đường thẳng $y=\frac{1-4x}{2}$ là

A. –4.

B. 1.

C. $\frac{1}{2}$.

D. –2.

Lời giải:

Đáp án đúng là: D

Ta có $y=\frac{1-4x}{2}=\frac{1}{2}-\frac{4}{2}x=-2x+\frac{1}{2}$.

Do đó, hệ số góc là –2.

Câu 6 trang 35 SBT Toán 8 Tập 2: Giá trị m để đường thẳng y = (m – 1)x + 3 (m ≠ 1) song song với đường thẳng y = x là

A. m = 2;

B. m = 1;

C. m = 0;

D. Không có giá trị của m.

Lời giải:

Đáp án đúng là: A

Đường thẳng y = (m – 1)x + 3 (m ≠ 1) song song với y = x khi và chỉ khi:

m – 1 = 1

m = 2 (thỏa mãn).

Câu 7 trang 35 SBT Toán 8 Tập 2: Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y = –x + 2 và cắt trục tung tại điểm có tung độ bằng 1 là

A. y = x + 1;

B. y = –x + 1;

C. y = 1;

D. Không có hàm số nào.

Lời giải:

Đáp án đúng là: B

Gọi hàm số cần tìm là: y = ax + b (a ≠ 0).

Đồ thị hàm số là đường thẳng song song với đường thẳng y = –x + 2 nên a = –1 và b ≠ 2.

Đường thẳng cắt trục tung tại điểm có tung độ bằng 1 nên đi qua điểm (0; 1) nên ta có:

1 = –0 + b

b = 1 (thỏa mãn)

Vậy hàm số cần tìm là: y = –x + 1.

Câu 8 trang 35 SBT Toán 8 Tập 2: Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y = –2x và đi qua điểm A(1; –1) là

A. y = 2x + 1;

B. y = –2x + 1;

C. y = 1;

D. Không có hàm số nào.

Lời giải:

Đáp án đúng là: B

Gọi hàm số cần tìm là: y = ax + b (a ≠ 0).

Đồ thị hàm số là đường thẳng song song với đường thẳng y = –2x nên a = –2 và b ≠ 0.

Đường thẳng qua điểm (1; –1) nên ta có:

–1 = –2 . 1 + b

b = 1 (thỏa mãn)

Vậy hàm số cần tìm là: y = –2x + 1.

Câu 9 trang 35 SBT Toán 8 Tập 2: Giá trị m để phương trình (m – 2)x + 4 – m^2 = 0 có vô số nghiệm là

A. m ≠ 2;

B. m = –2;

C. m = 0;

D. m = 2.

Lời giải:

Đáp án đúng là: D

Ta có:

(m – 2)x + 4 – m² = 0

(m – 2)x = m² – 4

Để phương trình có vô số nghiệm thì m – 2 = m² – 4 = 0 hay m = 2.

Câu 10 trang 35 SBT Toán 8 Tập 2: Giá trị m để phương trình (m^2 – 9)x + 3 – m = 0 vô nghiệm là

A. m ≠ ±3;

B. m = 3;

C. m = –3;

D. m = 0.

Lời giải:

Đáp án đúng là: C

Ta có:

(m² – 9)x + 3 – m = 0

(m² – 9)x = m – 3

Để phương trình vô nghiệm thì m² – 9 = 0 và m – 3 ≠ 0

Suy ra: m = ±3 và m ≠ 3

Vậy m = –3.

BÀI TẬP

Câu 7.41 trang 36 SBT Toán 8 Tập 2: Giải các phương trình sau:

a) 5(x – 1) – (6 – 2x) = 8x – 3;

b) $\frac{2x-1}{3}-\frac{5-3x}{2}=\frac{x+7}{4}$.

Lời giải:

a)

5(x – 1) – (6 – 2x) = 8x – 3

5x – 5 – 6 + 2x = 8x – 3

7x – 11 = 8x – 3

–x = 8

x = –8

Vậy tập nghiệm của phương trình là S = {–8}.

b)

$\frac{2x-1}{3}-\frac{5-3x}{2}=\frac{x+7}{4}$

$\frac{4\left(2x-1\right)}{12}-\frac{6\left(5-3x\right)}{12}=\frac{3\left(x+7\right)}{12}$

4(2x – 1) – 6(5 – 3x) = 3(x + 7)

8x – 4 – 30 + 18x = 3x + 21

26x – 34 = 3x + 21

23x = 55

x =$\frac{55}{23}$

Vậy tập nghiệm của phương trình là S = $\left\{\frac{55}{23}\right\}$.

Câu 7.42 trang 36 SBT Toán 8 Tập 2: Với hãng taxi A, số tiền khách phải trả khi di chuyển trên quãng đường không quá 30 km được cho bởi công thức sau:

T (x) = 12x + 10 (nghìn đồng),

trong đó 0 ≤ x ≤ 30 là số ki lô mét mà khách hàng đã di chuyển.

a) Tính số tiền khách phải trả khi di chuyển 15 km.

b) Nếu một người khách phải trả số tiền là 250 nghìn đồng thì người đó đã di chuyển bao nhiêu ki lô mét ?

Lời giải:

a) Thay x = 15 vào T(x) ta được: T(15) = 12 . 15 + 10 = 190.

Vậy số tiền khách phải trả khi di chuyển 15 km là 190 nghìn đồng.

b) Nếu một người khách phải trả số tiền là 250 nghìn đồng thì T = 250, thay vào T(x) ta có:

12x + 10 = 250

12x = 240

x = 20 (thỏa mãn)

Vậy vị khách đó di chuyển 20 km.

Câu 7.43 trang 36 SBT Toán 8 Tập 2: Theo kế hoạch, hai tổ sản xuất phải làm 900 sản phẩm. Do cải tiến kĩ thuật nên tổ I vượt mức 15% và tổ II vượt mức 10% so với kế hoạch. Vì vậy hai tổ vượt mức được 110 sản phẩm. Hỏi mỗi tổ đã sản xuất được bao nhiêu sản phẩm ?

Lời giải:

Gọi x là số sản phẩm tổ I sản xuất theo kế hoạch. (x > 0, x ∈ ℕ, x < 900)

Và y là số sản phẩm tổ II sản xuất theo kế hoạch. (y > 0, y ∈ ℕ, y < 900)

Do hai tổ sản xuất phải làm 900 sản phẩm nên ta có:

x + y = 900, suy ra y = 900 – x.

Vì cải tiến kĩ thuật nên tổ I vượt mức 15%, do đó tổ I sản xuất được số sản phẩm là:

115%x = 1,15x (sản phẩm).

Vì cải tiến kĩ thuật nên tổ II vượt mức 10%, do đó tổ II sản xuất được số sản phẩm là:

110%y = 1,1(900 – x) (sản phẩm).

Vì hai tổ vượt mức được 110 sản phẩm nên ta có:

1,15x + 1,1.(900 – x) = 900 + 110

1,15x + 990 – 1,1x = 1 010

0,05x = 20

x = 400 (thỏa mãn)

Suy ra y = 900 – 400 = 500 (thỏa mãn).

Vậy tổ I sản xuất được: 1,15 . 400 = 460 sản phẩm;

tổ II sản xuất được 1,1 . 500 = 550 sản phẩm.

Câu 7.44 trang 36 SBT Toán 8 Tập 2: Hòa 400 gam dung dịch NaCl loại I với 600 gam dung dịch NaCl loại II được một dung dịch NaCl có nồng độ phần trăm 27%. Tính nồng độ phần trăm của mỗi dung dịch NaCl loại I và loại II, biết rằng nồng độ phần trăm dung dịch NaCl loại I ít hơn nồng độ phần trăm dung dịch NaCl loại II là 5%

Lời giải:

Gọi x (%) là nồng độ phần trăm dung dịch NaCl loại I (0 < x < 100).

Do nồng độ phần trăm dung dịch NaCl loại I ít hơn nồng độ phần trăm dung dịch NaCl loại II là 5% nên ta có nồng độ phần trăm dung dịch NaCl loại II là: x + 5 (%).

Tổng khối lượng NaCl trong cả hai loại dung dịch là:

$\frac{x}{100}.400+\left(\frac{x+5}{100}\right).600=10x+30$ (g).

Theo đề bài, do hòa 400 gam dung dịch NaCl loại I với 600 gam dung dịch NaCl loại II được một dung dịch NaCl có nồng độ phần trăm 27% nên ta có phương trình:

$\frac{10x+30}{400+600}=\frac{27}{100}$

$\frac{10x+30}{1000}=\frac{27}{100}$

$\frac{x+3}{100}=\frac{27}{100}$

x + 3 = 27

x = 24 (thỏa mãn)

Vậy nồng độ phần trăm của mỗi dung dịch NaCl loại I là 24% và loại II có nồng độ phần trăm là: 24 + 5 = 29%.

Câu 7.45 trang 36 SBT Toán 8 Tập 2: Trong mỗi học kì, điểm đánh giá môn Toán gồm 4 điểm thường xuyên tính hệ số 1, điểm thi giữa kì tính hệ số 2 và điểm thi cuối học kì tính hệ số 3. Bạn An được 4 điểm thường xuyên là 8; 9; 10; 10 và điểm giữa kì là 8,5. Biết rằng điểm trung bình môn Toán của bạn An là 9,0. Hỏi bạn An được mấy điểm thi cuối học kì ?

Lời giải:

Gọi x là điểm thi cuối học kì của An (0 < x < 10).

Do điểm trung bình môn Toán của An là 9,0 nên ta có:

(8 + 9 + 10 + 10 + 8,5 . 2 + x . 3) : 9 = 9,0

54 + 3x = 81

3x = 27

x = 9 (thỏa mãn)

Vậy bạn An được 9 điểm thi cuối học kì.

Câu 7.46 trang 36 SBT Toán 8 Tập 2: Cho hàm số $y=\left(2m-1\right)x+5\left(m\ne \frac{1}{2}\right)$

a) Tìm m để đồ thị hàm số song song với đường thẳng y = –3x.

b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a.

c) Tìm giao điểm A của đồ thị hàm số ở câu b và đồ thị của hàm số y = x + 5. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y = x + 5 với trục Ox.

a) Để đồ thị hàm số song song với đường thẳng y = –3x thì:

2m – 1 = –3

2m = –2

m = –1 (thỏa mãn).

Vậy m = – 1 thì thỏa mãn yêu cầu bài toán.

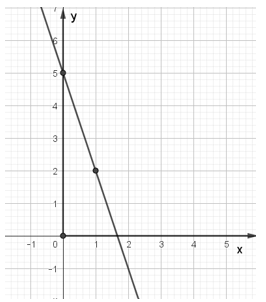
b) Với m = – 1, ta có hàm số y = –3x + 5.

Đồ thị hàm số y = –3x + 5 là đường thẳng đi qua các điểm (0; 5) và (1; 2).

Đồ thị hàm số như hình vẽ dưới:

c) Gọi tọa độ của điểm A(x₀; y₀)

Do A là giao điểm của y = –3x + 5 và y = x + 5 nên ta có:

–3x₀ + 5 = x₀ + 5

–4x₀ = 0

x₀ = 0

Suy ra y₀ = 0 + 5 = 5.

Do đó, điểm A(0; 5).

Gọi tọa độ của điểm B(x₁; y₁)

Do B là giao điểm của y = x + 5 với trục Ox nên ta có:

0 = x₁ + 5

x₁ = –5

Do đó, B(–5; 0).

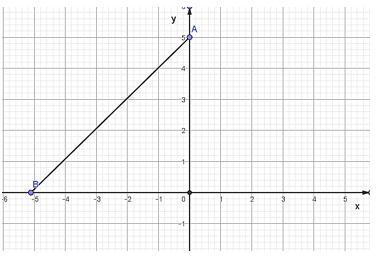
Biểu diễn các điểm A, B nên mặt phẳng Oxy ta có:

Dễ thấy: OA = 5; OB = 5.

Diện tích tam giác OAB vuông tại O là:$\frac{1}{2}\mathrm{.5.5}=\frac{25}{2}$.

Câu 7.47 trang 37 SBT Toán 8 Tập 2: Cho đường thẳng y = mx – 4 (m ≠ 0). Tìm m sao cho

a) Đường thẳng đã cho cắt đường thẳng y = –2x + 1 tại điểm có hoành độ bằng 2.

b) Đường thẳng đã cho cắt đường thẳng y = 3x – 2 tại điểm có tung độ bằng 4.

Lời giải:

a) Đường thẳng y = mx – 4 cắt đường thẳng y = –2x + 1 tại điểm có hoành độ bằng 2 nên ta có:

m . 2 – 4 = –2 . 2 + 1

2m – 4 = –3

2m = 1

m = $\frac{1}{2}$ (thỏa mãn).

Vậy m = $\frac{1}{2}$ .

b) Đường thẳng đã cho cắt đường thẳng y = 3x – 2 tại điểm có tung độ bằng 4 nên ta có hoành độ giao điểm thỏa mãn:

4 = 3x – 2

3x = 6

x = 2.

Do đó đường thẳng y = mx – 4 đi qua điểm (2; 4) nên ta có:

4 = m . 2 – 4

2m = 8

m = 4 (thỏa mãn).

Vậy m = 4.

Câu 7.48 trang 37 SBT Toán 8 Tập 2: Một công ty cho thuê thuyền du lịch tính phí thuê thuyền là 1 triệu đồng, ngoài ra tính phí sử dụng 500 nghìn đồng một giờ.

a) Viết công thức của hàm số biểu thị tổng chi phí y (nghìn đồng) để thuê một chiếc thuyền du lịch trong x (giờ).

b) Vẽ đồ thị của hàm số thu được ở câu a để tìm tổng chi phí cho một lần thuê trong 3 giờ.

c) Giao điểm của đồ thị với trục tung biểu thị điều gì ?

Lời giải:

a) 1 triệu đồng = 1 000 nghìn đồng.

Hàm số biểu thị tổng chi phí y (nghìn đồng) để thuê một chiếc thuyền du lịch trong x (giờ) là: y = 1 000 + 500x (nghìn đồng).

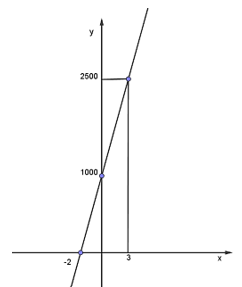
b) Đồ thị hàm số y = 1 000 + 500x đi qua hai điểm (–2; 0) và (0; 1 000) nên đồ thị hàm số như hình dưới.

Tổng chi phí cho một lần thuê trong x = 3 giờ tương ứng với điểm y = 2 500 nghìn đồng = 2 triệu 500 nghìn đồng.

c) Giao điểm của đồ thị với trục tung là điểm (0; 1 000). Giao điểm này biểu thị chi phí cố định khi thuê thuyền, dù không sử dụng giờ nào (tức là x = 0) vẫn phải trả phí 1 triệu đồng này, nếu đặt thuê.

Câu 7.49 trang 37 SBT Toán 8 Tập 2: Chị Lan vay mẹ 900 nghìn đồng và dự định trả cho mẹ 100 nghìn đồng mỗi tuần

a) Viết công thức của hàm số biểu thị số tiền y (nghìn đồng) mà chị Lan còn nợ mẹ sau x (tuần) vay.

b) Vẽ đồ thị của hàm số thu được ở câu a. Từ đó, tìm số tiền mà chị Lan nợ mẹ sau 4 tuần.

c) Giao điểm của đồ thị với trục hoành biểu thị điều gì ?

Lời giải:

a) Công thức của hàm số biểu thị số tiền y (nghìn đồng) mà chị Lan còn nợ mẹ sau x (tuần) vay là: y = 900 – 100x (nghìn đồng).

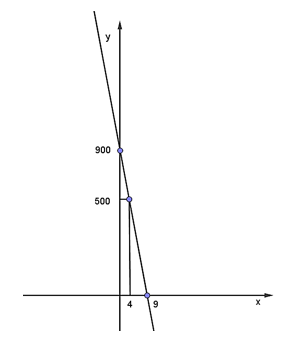
b) Đồ thị hàm số thu được ở câu a đi qua hai điểm (0; 900) và (9; 0) nên ta có đồ thị hàm số như hình dưới:

Số tiền mà Lan nợ mẹ sau 4 tuần, tức x = 4 là y = 900 – 100 . 4 = 500 (nghìn đồng).

c) Giao điểm của đồ thị với trục hoành là điểm (0; 9). Giao điểm này biểu thị số tuần cần thiết để Lan trả hết nợ cho mẹ (số tiền y Lan nợ mẹ lúc này bằng 0).

Câu 7.50 trang 37 SBT Toán 8 Tập 2: Giả sử rằng lượng cung S và lượng cầu D về áo phông tại một buổi biểu diễn được cho bởi các hàm số sau:

S(p) = –600 + 10p ; D(p) = 1 200 – 20p,

trong đó p (nghìn đồng) là giá của một chiếc áo phông.

a) Tìm mức giá cân bằng (tức là mức giá mà lượng cung bằng lượng cầu) của áo phông tại buổi biểu diễn này.

b) Vẽ đồ thị của hai hàm số S(p) và D(p) trên cùng một hệ trục tọa độ.

c) Từ kết quả câu b, xác định mức giá của áo phông mà lượng cung lớn hơn lượng cầu. Khi đó, điều gì sẽ xảy ra ?

Lời giải:

a) Mức giá khi lượng cung bằng lượng cầu là giá trị x₀ thỏa mãn:

–600 + 10x₀ = 1 200 – 20x₀

30x₀ = 1 800

x₀ = 60

Vậy mức giá cân bằng là 60 nghìn đồng.

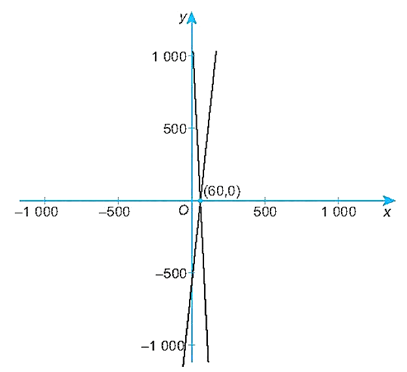
b) Đồ thị hàm số S(p) đi qua hai điểm (0; –600) và (60; 0).

Đồ thị hàm số D(p) đi qua hai điểm (0; 1 200) và (60; 0).

Đồ thị của hai hàm số được vẽ trong hình dưới:

c) Từ đồ thị trên, ta thấy khi giá của mỗi chiếc áo lớn hơn 60 nghìn đồng thì lượng cung lớn hơn lượng cầu. Khi đó sẽ có một lượng áo phông bị tồn kho (do không bán được).

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 29: Hệ số góc của đường thẳng

Bài 30: Kết quả có thể và kết quả thuận lợi

Bài 31: Cách tính xác suất của biến cố bằng tỉ số

Bài 32: Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng

Bài tập cuối chương 8 trang 46