Sách bài tập Toán 8 (Kết nối tri thức) Bài tập cuối chương 4

Giải SBT Toán 8 Bài tập cuối chương 4

A. Câu hỏi (Trắc nghiệm)

Câu 1 trang 53 SBT Toán 8 Tập 1: Cho tam giác ABC có BC = 13 cm. E và F lần lượt là trung điểm của AB, AC. Độ dài EF bằng:

A. 13 cm.

B. 26 cm.

C. 6,5 cm.

D. 3 cm.

Lời giải:

Đáp án đúng là: C

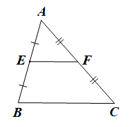
Trong ∆ABC có E và F lần lượt là trung điểm của AB, AC nên EF là đường trung bình của ∆ABC.

Suy ra $MN=\frac{1}{2}BC=\frac{1}{2}\cdot 13=\mathrm{6,5}$(cm) (tính chất đường trung bình của tam giác).

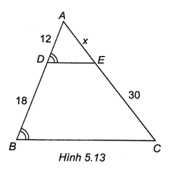
Câu 2 trang 53 SBT Toán 8 Tập 1: Độ dài x trong Hình 5.13 là

A. 20.

B. 50.

C. 12.

D. 30.

Lời giải:

Đáp án đúng là: A

Ta có $\widehat{ADE}=\widehat{ABC}$, mà hai góc này ở vị trí đồng vị nên DE // BC

Trong ∆ABC có DE // BC, theo Định lí Thalès ta có: $\frac{AD}{DB}=\frac{AE}{EC}$

Hay $\frac{12}{18}=\frac{AE}{30}$ nên $AE=\frac{12\cdot 30}{18}=20$

Vậy x = AE = 20.

Câu 3 trang 53 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại B. Hai trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GB, GC. Khẳng định nào đúng?

A. $MN=\frac{1}{2}AC.$

B. $BC=\frac{1}{2}IK.$

C. MN > IK.

D. MN = IK.

Lời giải:

Đáp án đúng là: D

Trong ∆ABC có M là trung điểm của BC, N là trung điểm của AC nên MN là đường trung bình của ∆ABC

Suy ra $MN=\frac{1}{2}AB$ (tính chất đường trung bình trong tam giác). (1)

Trong ∆BGC có I là trung điểm của BG, K là trung điểm của BC nên IK là đường trung bình của ∆BGC

Suy ra $IK=\frac{1}{2}BC$ (tính chất đường trung bình trong tam giác). (2)

Mà tam giác ABC cân tại B nên BA = BC (3)

Từ (1), (2), (3) suy ra MN = IK.

Câu 4 trang 53 SBT Toán 8 Tập 1: Cho hình thang ABCD (AB // DC), O là giao điểm của AC và BD. Xét các khẳng định sau:

$\left(1\right)\frac{OA}{OC}=\frac{OD}{OB};$

$\left(2\right)OA\cdot OD=OB\cdot OC;$

$\left(3\right)\frac{AO}{AC}=\frac{BO}{BD}.$

Số khẳng định đúng là:

A. 0.

B. 1.

C. 2.

D. 3.

Lời giải:

Đáp án đúng là: C

Qua O kẻ OM // AB // CD (M ∈ AD).

Xét DADC có OM // CD, theo định lí Thalès ta có $\frac{OA}{OC}=\frac{MA}{MD};\frac{AO}{AC}=\frac{AM}{AD}$

Xét DABD có OM // AB, theo định lí Thalès ta có $\frac{OB}{OD}=\frac{MA}{MD};\frac{BO}{BD}=\frac{AM}{AD}$

Suy ra $\frac{OA}{OC}=\frac{OB}{OD}=\frac{MA}{MD}\left(*\right)$ và $\frac{AO}{AC}=\frac{BO}{BD}=\frac{AM}{AD}$

Do đó khẳng định (1) là sai và khẳng định (3) là đúng.

Từ (*) suy ra OA.OD = OB.OC. Do đó khẳng định (2) đúng.

Vậy có 2 khẳng định đúng.

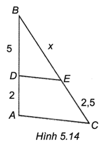
Câu 5 trang 53 SBT Toán 8 Tập 1: Cho Hình 5.14, biết DE // AC. Độ dài x là

A. 5.

B. 7.

C. 6,5.

D. 6,25.

Lời giải:

Đáp án đúng là: D

Xét ∆ABC có DE // AC, theo Định lí Thalès ta có $\frac{BD}{DA}=\frac{BE}{EC}$

Hay $\frac{5}{2}=\frac{BE}{\mathrm{2,5}}$, suy ra $BE=\frac{5\cdot \mathrm{2,5}}{2}=\mathrm{6,25.}$

Vậy x = 6,25.

Câu 6 trang 54 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Biết AG = 4 cm, độ dài của EI, DK là

A. EI = DK = 3 cm.

B. El = 3 cm; DK = 2 cm.

C. EI = DK = 2 cm.

D. EI = 1 cm; DK = 2 cm.

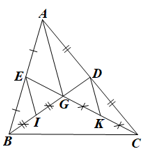
Lời giải:

Đáp án đúng là: C

Vì BD, CE là các đường trung tuyến của ∆ABC nên D là trung điểm của AC, E là trung điểm của AB.

• Trong ∆ABG có: E là trung điểm của AB, I là trung điểm của GB nên EI là đường trung bình của ∆ABG

Suy ra $EI=\frac{1}{2}AG$ (tính chất đường trung bình trong tam giác)

Do đó $EI=\frac{1}{2}\cdot 4=2$ (cm).

• Trong ∆ACG có: D là trung điểm của AC, K là trung điểm của GC nên DK là đường trung bình của ∆ACG

Suy ra $DK=\frac{1}{2}AG$ (tính chất đường trung bình trong tam giác)

Do đó $DK=\frac{1}{2}\cdot 4=2$ (cm).

Vậy EI = DK = 2 cm.

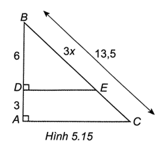
Câu 7 trang 54 SBT Toán 8 Tập 1: Cho Hình 5.15, biết ED ⊥ AB, AC ⊥ AB. Khi đó, x có giá trị là

Lời giải:

Đáp án đúng là: C

Ta có AB = AD + BD = 3 + 6 = 9

Do ED ⊥ AB, AC ⊥ AB nên DE // AC

Trong ∆ABC có DE // AC nên theo định lí Thalès ta có: $\frac{BD}{BA}=\frac{BE}{BC}$

Suy ra $BE=\frac{BD\cdot BC}{BA}=\frac{6\cdot \mathrm{13,5}}{9}=9$ hay 3x = 9

Vậy x = 9 : 3 = 3.

Câu 8 trang 54 SBT Toán 8 Tập 1: Cho ∆ABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Độ dài x bằng

A. 4.

B. 6.

C. 12.

D. 14.

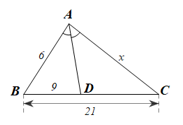
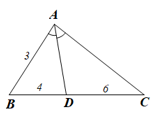
Lời giải:

Ta có: BC = BD + DC nên DC = BC ‒ BD = 21 ‒ 9 = 12.

Trong ∆ABC, AD là phân giác của $\widehat{BAC}$ nên $\frac{AB}{AC}=\frac{DB}{DC}$ (tính chất đường phân giác của tam giác)

Hay $\frac{6}{x}=\frac{9}{12}$, suy ra $x=\frac{6\cdot 12}{9}=8.$

Vậy không có phương án nào đúng do x = 8.

Câu 9 trang 54 SBT Toán 8 Tập 1: Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết AB = 3 cm, BD = 4 cm, CD = 6 cm. Độ dài AC bằng

A. 4 cm.

B. 5 cm.

C. 6 cm.

D. 4,5 cm.

Lời giải:

Đáp án đúng là: D

Trong ∆ABC có AD là phân giác của góc A nên $\frac{AB}{AC}=\frac{DB}{DC}$(tính chất đường phân giác của tam giác)

Hay $\frac{3}{AC}=\frac{4}{6}$, suy ra $AC=\frac{3\cdot 6}{4}=\mathrm{4,5}$(cm).

Câu 10 trang 54 SBT Toán 8 Tập 1: Cho ∆ABC đều, cạnh 3 cm; M, N lần lượt là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng

A. 8 cm.

B. 7,5 cm.

C. 6 cm.

D. 7 cm.

Lời giải:

Đáp án đúng là: B

Trong ∆ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của ∆ABC

Suy ra $MN=\frac{1}{2}BC$ (tính chất đường trung bình của tam giác)

Hay $MN=\frac{1}{2}\cdot 3=\mathrm{1,5}$(cm)

Do ∆ABC đều nên AB = AC

Lại có M, N lần lượt là trung điểm của AB và AC nên $BM=\frac{1}{2}AB=\frac{1}{2}AC=CN$

Hay $BM=CN=\frac{1}{2}\cdot 3=\mathrm{1,5}$ (cm).

Vậy chu vi của tứ giác BMNC là:

BM + MN + NC + BC = 1,5 + 1,5 + 1,5 + 3 = 7,5 (cm).

Câu 11 trang 54 SBT Toán 8 Tập 1: Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Gọi H, I, K lần lượt là trung điểm của AB, BC, AC. Chu vi của tứ giác AHIK bằng

A. 7 cm.

B. 14 cm.

C. 24 cm.

D. 12 cm.

Lời giải:

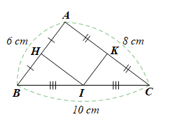
Đáp án đúng là: B

Ta có: BC² = 10² = 100, AB² + BC² = 6² + 8² = 36 + 64 = 100

Suy ra BC² = AB² + BC²

Do đó, ∆ABC vuông tại A (định lý Pythagore đảo).

Trong ∆ABC có:

• H, I lần lượt là trung điểm của AB và BC nên HI là đường trung bình của ∆ABC;

Suy ra HI // AC và $HI=\frac{1}{2}AC$(tính chất đường trung bình trong tam giác)

Hay $HI=\frac{1}{2}\cdot 8=4$(cm).

• I, K lần lượt là trung điểm của BC và AC nên IK là đường trung bình của ∆ABC

Suy ra IK // AB và $IK=\frac{1}{2}AB$(tính chất đường trung bình trong tam giác)

Hay $IK=\frac{1}{2}\cdot 6=3$(cm).

Ta có ∆ABC vuông tại A nên AB ⊥ AC, mà HI // AC nên AB ⊥ HI

Lại có IK // AB nên HI ⊥ IK tại I

Tứ giác AHIK có: $\widehat{HAK}=\widehat{IHA}=\widehat{IKA}=90°$ nên AHIK là hình chữ nhật.

Chu vi của tứ giác AHIK bằng: 2.(IH + IK) = 2.(4 + 3) = 14 (cm).

Câu 12 trang 54 SBT Toán 8 Tập 1: Cho hình thoi ABCD có M là trung điểm AD, đường chéo AC cắt BM tại điểm E. (H.5.16)

Tỉ số $\frac{EM}{EB}$ bằng

A. $\frac{1}{3}$.

B. 2.

C. $\frac{1}{2}$.

D. $\frac{2}{3}$.

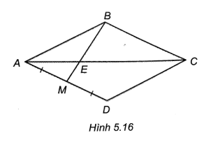
Lời giải:

Đáp án đúng là: C

Do ABCD là hình thoi nên AC là phân giác của góc A

Trong ∆ABM có AE là phân giác của góc $\widehat{BAM}$ nên $\frac{EM}{EB}=\frac{AM}{AB}$ (tính chất đường phân giác trong tam giác)

Mà M là trung điểm của AD nên $AM=\frac{1}{2}AD=\frac{1}{2}AB$ (do ABCD là hình thoi nên AB = AD)

Suy ra $\frac{EM}{EB}=\frac{\frac{1}{2}AB}{AB}=\frac{1}{2}$.

B. Bài tập

Bài 4.15 trang 55 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm I nằm trong tam giác. Lấy điểm D trên IA, qua D kẻ đường thẳng song song với AB, cắt IB tại E. Qua E kẻ đường thẳng song song với BC, cắt IC tại F. Chứng minh rằng: DF // AC.

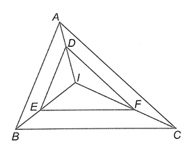
Lời giải:

Trong ∆AID có DE // AB suy ra $\frac{ID}{IA}=\frac{IE}{IB}$(định lí Thalès)

Trong ∆IBC có EF // BC suy ra $\frac{IE}{IB}=\frac{IF}{IC}$(định lí Thalès).

Suy ra $\frac{ID}{IA}=\frac{IF}{IC}$

Trong ∆AIC có $\frac{ID}{IA}=\frac{IF}{IC}$ nên DF // AC (định lí Thalès đảo).

Bài 4.16 trang 55 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh MI = IK = KN.

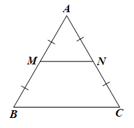
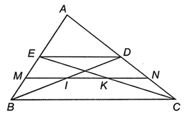
Lời giải:

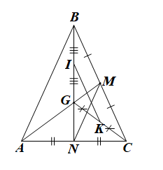
Trong ∆ABC có các đường trung tuyến BD, CE nên D là trung điểm của AC, E là trung điểm của AB nên ED là đường trung bình của ∆ABC

Suy ra $ED=\frac{1}{2}BC$ và ED // BC (tính chất đường trung bình của tam giác)

Ta có: E là trung điểm của AB nên $AE=EB=\frac{1}{2}AB$

Mà M là trung điểm của EB nên $EM=MB=\frac{1}{2}EB=\frac{1}{4}AB$ hay $\frac{MB}{AB}=\frac{1}{4}$

Tương tự, ta cũng có $NC=\frac{1}{4}AC$ hay $\frac{NC}{AC}=\frac{1}{4}$

Suy ra $\frac{MB}{AB}=\frac{NC}{AC}\left(=\frac{1}{4}\right)$

Xét DABC có $\frac{MB}{AB}=\frac{NC}{AC}$ nên MN // BC (định lí Thalès đảo)

Lại có ED // BC nên ED // MN // BC.

Xét DBDE có M là trung điểm của EB và MI // ED (do ED // MN)

Suy ra I là trung điểm của BD hay IB = ID

Khi đó MI là đường trung bình của DBDE nên $MI=\frac{1}{2}ED$.

Tương tự, trong DCDE ta cũng có $KN=\frac{1}{2}ED,$ trong DBCE có $MK=\frac{1}{2}BC$.

Ta có $IK=MK-MI=\frac{1}{2}BC-\frac{1}{2}ED=ED-\frac{1}{2}ED=\frac{1}{2}ED$.

Do đó $MI=IK=KN=\frac{1}{2}ED$.

Bài 4.17 trang 55 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh DE // BC.

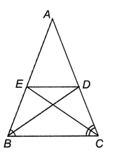
Lời giải:

Trong ∆ABC có BD là phân giác của $\widehat{ABC}$ nên $\frac{DA}{DC}=\frac{BA}{BC}$ (tính chất đường phân giác của tam giác). (1)

Trong ∆ABC có CE là phân giác của $\widehat{ACB}$ nên $\frac{EA}{EB}=\frac{CA}{CB}$(tính chất đường phân giác trong tam giác). (2)

Mà ∆ABC cân tại A nên AB = AC  (3)

Từ (1), (2), (3), suy ra: $\frac{DA}{DC}=\frac{EA}{EB}$.

Xét DABC có $\frac{DA}{DC}=\frac{EA}{EB}$, suy ra ED // BC (định lí Thales đảo).

Bài 4.18 trang 55 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, điểm E thuộc cạnh AB (E khác A và B), điểm F thuộc cạnh AD (F khác A và D). Đường thẳng qua D song song với EF cắt AC tại I. Đường thẳng qua B song song với EF cắt AC tại K.

a) Chứng minh rằng: AI = CK.

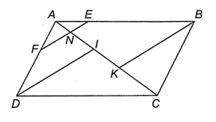
b) Gọi N là giao điểm của EF và AC. Chứng minh rằng: $\frac{AB}{AE}+\frac{AD}{AF}=\frac{AC}{AN}$.

Lời giải:

a) Ta có DI // EF và BK // EF nên EF // DI // BK

Do DI // BK nên $\widehat{CID}=\widehat{AKB}$(hai góc so le trong)

Mà $\widehat{AID}+\widehat{CID}=180°;\widehat{CKB}+\widehat{AKB}=180°$

Suy ra $\widehat{AID}=\widehat{CKB}$(1)

Do ABCD là hình bình hành nên AD = BC và AD // BC

Suy ra $\widehat{DAC}=\widehat{BCA}$(so le trong) hay $\widehat{DAI}=\widehat{BCK}$(2)

Xét DADI có $\widehat{AID}+\widehat{DAI}+\widehat{ADI}=180°$(3)

Xét DCBK có $\widehat{CKB}+\widehat{BCK}+\widehat{CBK}=180°$(4)

Từ (1), (2), (3) và (4) suy ra $\widehat{ADI}=\widehat{CBK}$

Xét DADI và DCBK có:

(cmt); AD = BC (cmt); (cmt)

Do đó DADI = DCBK (g.c.g)

Suy ra AI = CK (hai cạnh tương ứng).

b) Trong ∆ABK có NE // BK nên $\frac{AB}{AE}=\frac{AK}{AN}$(định lí Thalès).

Trong ∆ADI có FN // DI nên $\frac{AD}{AF}=\frac{AI}{AN}$(định lí Thalès),

Mà AI = CK (câu a) nên $\frac{AD}{AF}=\frac{CK}{AN}$

Suy ra $\frac{AB}{AE}+\frac{AD}{AF}=\frac{AK}{AN}+\frac{CK}{AN}=\frac{AK+CK}{AN}=\frac{AC}{AN}$

Bài 4.19 trang 55 SBT Toán 8 Tập 1: Cho góc xOy nhọn. Trên cạnh Ox lấy điểm N, trên cạnh Oy lấy điểm M. Gọi I là một điểm trên đoạn thẳng MN. Qua I kẻ đường thẳng song song với Ox cắt Oy tại A (A khác M và N) và đường thẳng song song với Oy cắt Ox ở B. Chứng minh rằng: $\frac{MA}{MO}+\frac{NB}{NO}=1.$

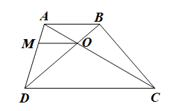
Lời giải:

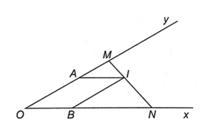
Xét ∆OMN có AI // ON nên $\frac{MA}{MO}=\frac{MI}{MN}$(định lí Thalès);

Và IB // MO nên $\frac{NB}{NO}=\frac{NI}{NM}$(định lí Thalès).

Suy ra $\frac{MA}{MO}+\frac{NB}{NO}=\frac{MI}{MN}+\frac{NI}{NM}=\frac{MI+NI}{MN}=\frac{MN}{MN}=1$.

Bài 4.20 trang 55 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, AC cắt BD tại O. Đường phân giác góc A cắt BD tại M, đường phân giác D cắt AC tại N. Chứng minh MN // AD.

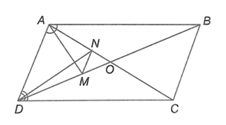
Lời giải:

Trong ∆ABD có: AM là phân giác của góc $\widehat{BAD}$ nên $\frac{AB}{AD}=\frac{MB}{MD}$(tính chất đường phân giác trong tam giác)

Tương tự: trong ∆ADC có DN là phân giác góc $\widehat{ADC}$ nên $\frac{DC}{DA}=\frac{NC}{NA}$

Mà AB = DC (do ABCD là hình bình hành) suy ra $\frac{MB}{MD}=\frac{NC}{NA}$.

Từ đó, ta có: $\frac{MB}{MD}+1=\frac{NC}{NA}+1$ hay $\frac{MB+MD}{MD}=\frac{NC+NA}{NA}$ 

Suy ra $\frac{BD}{MD}=\frac{AC}{NA}$(1)

Mà ABCD là hình bình hành nên 2 đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường, suy ra BD = 2DO, AC = 2AO (2)

Từ (1) và (2) suy ra $\frac{2DO}{DM}=\frac{2AO}{AN}$ hay $\frac{DO}{DM}=\frac{AO}{AN}$

Xét $∆$OAD có $\frac{DO}{DM}=\frac{AO}{AN}$ nên MN // AD (định lí Thalès đảo).

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác: 

Bài 17: Tính chất đường phân giác của tam giác

Bài 18: Thu thập và phân loại dữ liệu

Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

Bài tập cuối chương 5