Sách bài tập Toán 8 Bài 28 (Kết nối tri thức): Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Giải SBT Toán 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Bài tập 7.25 trang 30 SBT Toán 8 Tập 2: Cho hàm số y = (1 – 2m)x + 3.

a) Với những giá trị nào của m thì hàm số đã cho là hàm số bậc nhất ?

b) Tìm m, biết đồ thị hàm số đã cho đi qua điểm (–1; 4).

c) Với giá trị m tìm được ở câu b, hãy hoàn thành bảng giá trị sau vào vở:

Lời giải:

a) Để hàm số y = (1 – 2m)x + 3 là hàm số bậc nhất thì 1 – 2m ≠ 0 hay m ≠ $\frac{1}{2}$ .

b) Đồ thị hàm số đã cho đi qua điểm (–1; 4) nên ta có khi x = –1 thì y = 4.

Thay vào công thức hàm số ta có:

4 = (1 – 2m).(–1) + 3

4 = –1 + 2m + 3

2m = 2

m = 1.

Vậy m = 1.

c) Với m = 1 ta có công thức hàm số y = –x + 3.

Ta có:

Khi x = –2 thì y = –(–2) + 3 = 5;

Khi x = –1 thì y = –(–1) + 3 = 4;

Khi x = 0 thì y = –0 + 3 = 3;

Khi x = 1 thì y = –1 + 3 = 2;

Khi x = 2 thì y = –2 + 3 = 1.

Do đó, ta có bảng dưới đây

Bài tập 7.26 trang 30 SBT Toán 8 Tập 2: Vẽ đồ thị của các hàm số sau

a) y = 2x + 3;

b) y = –3x + 5;

c) y = $\frac{1}{2}$x;

d) y =$-\frac{3}{2}x$.

Lời giải:

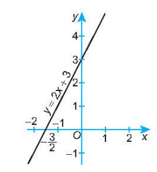
a) Khi x = 0 thì y = 3;

Khi x = thì y = 0.

Đồ thị của hàm số y = 2x + 3 là một đường thẳng đi qua hai điểm (0; 3) và .$\left(\frac{-3}{2};0\right)$

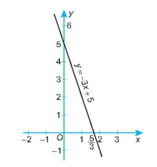
b) Khi x = 0 thì y = 5;

Khi x = thì y = 0.

Đồ thị của hàm số y = –3x + 5 là một đường thẳng đi qua hai điểm (0; 5) và $\left(\frac{5}{3};0\right)$

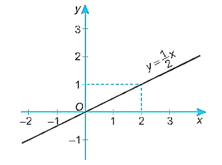
c) Khi x = 0 thì y = 0;

Khi x = 2 thì y = 1.

Đồ thị của hàm số y = $\frac{1}{2}$x là đường thẳng đi qua điểm (0; 0) và (2; 1).

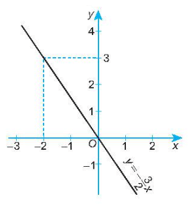
d) Khi x = 0 thì y = 0;

Khi x = – 2 thì y = 3.

Đồ thị của hàm số y = là đường thẳng đi qua hai điểm (0; 0) và (– 2; 3).

Bài tập 7.27 trang 30 SBT Toán 8 Tập 2: Cho ba đường thẳng

(d₁): y = –2x + 1 ; (d₂): y = x + 4 và (d₃): y = 2mx – 3 (m ≠ 0).

a) Tìm giao điểm của hai đường thẳng (d₁) và (d₂).

b) Xác định giá trị của m để ba đường thẳng đã cho đồng quy.

Lời giải:

a) Gọi I(x₀; y₀) là giao điểm của (d₁) và (d₂).

Khi đó, tọa độ điểm I thỏa mãn y₀ = –2x₀ + 1 và y₀ = x₀ + 4.

Suy ra –2x₀ + 1 = x₀ + 4

–3x₀ = 3

x₀ = –1

Do đó, y₀ = –1 + 4 = 3.

Vậy điểm I(–1; 3).

b)

Để ba đường thẳng đồng quy thì (d₃) phải đi qua I(–1; 3) tức là khi x = –1 thì y = 3. Thay vào công thức (d₃) ta có:

3 = 2m.(–1) – 3

–2m – 3 = 3

–2m = 6

m = –3

Vậy m = –3 thỏa mãn yêu cầu đề bài.

Bài tập 7.28 trang 30 SBT Toán 8 Tập 2: Một cửa hàng sửa chữa máy điều hòa không khí tính phí bao gồm 50 nghìn đồng cho một cuộc gọi dịch vụ và 80 nghìn đồng cho mỗi giờ nhân công. Viết hàm số biểu thị phí C (tính theo nghìn đồng) cho một cuộc gọi dịch vụ với x (giờ) lao động. Phí dịch vụ sẽ là bao nhiêu nếu có 3 giờ lao động.

Lời giải:

Với x (giờ) lao động thì phí là: 80x (nghìn đồng)

Do đó, phí C cho một cuộc gọi dịch vụ với x (giờ) lao động là: C = 50 + 80x.

Với 3 giờ lao động tức là x = 3 thì phí dịch vụ sẽ là: C = 50 + 80.3 = 290 (nghìn đồng).

Bài tập 7.29 trang 30 SBT Toán 8 Tập 2: Anh Nam đang tiết kiệm tiền để mua một chiếc máy tính mới với giá 15 triệu đồng. Anh Nam đã có 4,5 triệu đồng và dự định sẽ tiết kiệm 300 nghìn đồng mỗi tuần.

a) Viết hàm số y = f(x) biểu thị số tiền y (triệu đồng) mà anh Nam tiết kiệm được sau x (tuần).

b) Vẽ đồ thị của hàm số tìm được ở câu a. Từ đó xác định số tuần anh Nam sẽ tiết kiệm đủ tiền để mua chiếc máy tính đó.

Lời giải:

a)

Sau x (tuần) anh Nam tiết kiệm được số tiền là: 300x (nghìn đồng) = 0,3x (triệu đồng).

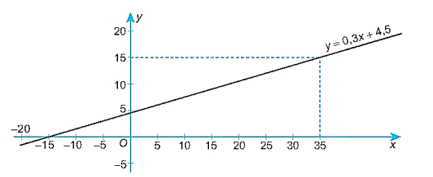
Hàm số y = f(x) biểu thị số tiền y (triệu đồng) mà anh Nam tiết kiệm được sau x (tuần) là y = 4,5 + 0,3x.

b)

Khi x = –15 thì y = 0.

Khi x = 0 thì y = 4,5.

Khi x = 35 thì y = 15.

Đồ thị hàm số y = 4,5 + 0,3x đi qua các điểm (–15; 0) ; (0; 4,5) ; (35; 15).

Từ đồ thị, ta thấy để anh Nam có đủ tiền tức là y = 15 khi đó x = 35.

Vậy anh Nam cần 35 tuần để tiết kiệm đủ tiền để mua chiếc máy tính đó.

Bài tập 7.30 trang 30 SBT Toán 8 Tập 2: Hải lí (còn gọi là dặm biển) là một đơn vị chiều dài hàng hải và 1 hải lí bằng 1,852 km

a) Viết công thức biểu thị y (km) theo x (hải lí). Giá trị âm của x có ý nghĩa gì trong tình huống này không ? Giải thích.

b) Vẽ đồ thị của hàm số y = f(x) nhận được ở câu a.

c) Một hành trình đi biển dài 350 hải lí. Hỏi hành trình đó dài bao nhiêu kilômét ?

Lời giải:

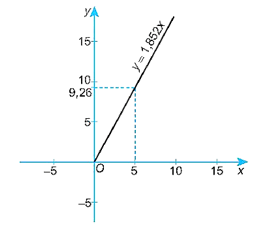
a) Vì 1 hải lí bằng 1,852 km nên ta có: y = 1,852x.

Giá trị âm của x trong trường hợp này không có ý nghĩa, vì chiều dài là một đại lượng không âm.

b)

Ta có:

Khi x = 0 thì y = 0.

Khi x = 5 thì y = 9,26.

Đồ thị của hàm số y = 1,852x (với x không âm) là một phần đường thẳng như hình bên, đi qua các điểm (0; 0) và (5; 9,26).

c) Một hành trình đi biển dài 350 hải lí. Tức là x = 350. Khi đó, hành trình dài số km là: y = 1,852 . 350 = 648,2 (km).

Bài tập 7.31 trang 31 SBT Toán 8 Tập 2: Một công ty cho thuê ô tô tính phí bao gồm 1,5 triệu đồng/ngày và 10 nghìn đồng cho mỗi kilômét di chuyển.

a) Viết hàm số bậc nhất biểu thị chi phí thuê xe mỗi ngày C (đơn vị nghìn đồng) theo x (km) đã di chuyển trong ngày.

b) Chi phí thuê xe trong ngày là bao nhiêu nếu trong ngày đó xe di chuyển quãng đường tổng cộng dài 180 km ?

Lời giải:

a)

1,5 triệu đồng = 1 500 nghìn đồng

Do thuê ô tô tính phí 1,5 triệu đồng/ngày và 10 nghìn đồng cho mỗi kilômét di chuyển nên hàm số biểu thị chi phí thuê xe mỗi ngày là: C = 1 500 + 10x (nghìn đồng).

b)

Chi phí thuê xe trong ngày nếu trong ngày đó xe di chuyển quãng đường tổng cộng dài 180 km là: C = 1500 + 10 . 180 = 3 300 (nghìn đồng).

Vậy C = 3,3 triệu đồng.

Bài tập 7.32 trang 31 SBT Toán 8 Tập 2: Giá trị sổ sách là giá trị của tài sản mà một công ty sử dụng để tạo ra bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm đi một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt vào tài sản. Giả sử rằng một công ty vận tải vừa mua một số ô tô mới với giá là 640 triệu đồng một chiếc. Công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe sẽ giảm giá 640 : 8 = 80 (triệu đồng).

a) Tìm hàm số bậc nhất biểu thị giá trị sổ sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó.

b) Vẽ đồ thị của hàm số bậc nhất tìm được ở câu a.

c) Giá trị sổ sách của mỗi chiếc xe sau 3 năm là bao nhiêu ?

d) Khi nào giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng ?

Lời giải:

a) Vì công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe sẽ giảm giá 640 : 8 = 80 (triệu đồng) nên ta có sau x năm thì mỗi chiếc xe giảm 80x (triệu đồng).

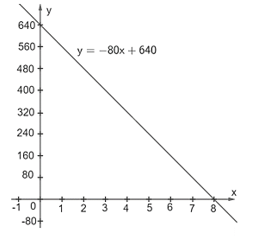
Hàm số bậc nhất biểu thị giá trị sổ sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó là: V = 640 – 80x = –80x + 640 (triệu đồng).

b) Hàm số V = –80x + 640 đi qua các điểm (0; 640) và (8; 0).

Đồ thị hàm số như hình dưới đây.

Chú ý: Vì số lớn nên ta chia khoảng cách giữa 2 trục Ox và Oy là khác nhau.

c) Giá trị sổ sách của mỗi chiếc xe sau x = 3 (năm) là:

V = –80.3 + 640 = 400 (triệu đồng).

d)

Để giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng thì:

V = 160

Hay:

–80x + 640 = 160

–80x = –480

x = 6

Vậy sau 6 năm thì giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng.

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 29: Hệ số góc của đường thẳng

Bài tập cuối chương 7 trang 35

Bài 30: Kết quả có thể và kết quả thuận lợi

Bài 31: Cách tính xác suất của biến cố bằng tỉ số

Bài 32: Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng