Sách bài tập Toán 8 (Kết nối tri thức): Bài tập cuối chương 9

Giải SBT Toán 8 Bài tập cuối chương 9

A. Trắc nghiệm

Câu 1 trang 68 SBT Toán lớp 8 Tập 2: Câu nào sau đây là sai ?

A. Hai tam giác có các cặp cạnh tương ứng tỉ lệ thì có các cặp góc tương ứng bằng nhau.

B. Hai tam giác có hai cặp góc tương ứng bằng nhau thì có cặp cạnh tương ứng tỉ lệ.

C. Hai tam giác có một cặp góc tương ứng bằng nhau và hai cặp cạnh tương ứng tỉ lệ thì đồng dạng với nhau.

D. Hai tam giác cùng đồng dạng với một tam giác theo cùng một tỉ số đồng dạng thì bằng nhau.

Lời giải:

Đáp án đúng là: C

Đáp án C sai vì hai tam giác đồng dạng khi có hai cặp cạnh tương ứng tỉ lệ và một cặp góc tạo bởi hai cạnh tương ứng bằng nhau thì đồng dạng với nhau.

Câu 2 trang 68 SBT Toán lớp 8 Tập 2: Bộ ba số đo nào dưới đây không là độ dài ba cạnh của một tam giác vuông ?

A. $\sqrt{2}$ cm, $\sqrt{2}$ cm, 2 cm.

B. 1 cm, 1 cm, $\frac{1}{\sqrt{2}}$ cm.

C. 2 cm, 4 cm, $\sqrt{20}$ cm.

D. 3 cm, 4 cm, 5 cm.

Lời giải:

Đáp án đúng là: B

Vì 1² + 1² = 2 ≠ ${\left(\frac{1}{\sqrt{2}}\right)}^2$ nên bộ ba số 1 cm, 1 cm, $\frac{1}{\sqrt{2}}$cm không là độ dài ba cạnh của một tam giác vuông

B. Bài tập

Bài 9.61 trang 68 SBT Toán lớp 8 Tập 2: Cho ∆ABC ᔕ ∆MNP với $\widehat{A}=60°$,$\widehat{N}=40°$ . Hãy tính số đo các góc còn lại của hai tam giác ABC và MNP.

Lời giải:

Vì ∆ABC ᔕ ∆MNP nên ta có:

$\widehat{A}=\widehat{M}=60°$;

$\widehat{B}=\widehat{N}=40°$;

$\widehat{C}=\widehat{P}$

Tam giác ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ nên $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-60°-40°=80°$ .

Suy ra: $\widehat{P}=\widehat{C}=80°$

Bài 9.62 trang 68 SBT Toán lớp 8 Tập 2: Cho ∆ABC ᔕ ∆MNP với AB = 5 cm, AC = 6 cm, BC = 7 cm. Biết rằng tam giác MNP có chu vi bằng 36 cm, hãy tính độ dài các cạnh của tam giác MNP và tỉ số đồng dạng của tam giác ABC với tam giác MNP.

Lời giải:

Chu vi tam giác ABC là: AB + BC + AC = 5 + 6 + 7 = 18 (cm).

Chu vi tam giác MNP bằng 36 cm nên ta có: MN + NP + MP = 36.

Vì ∆ABC ᔕ ∆MNP nên $\frac{BC}{NP}=\frac{AC}{MP}=\frac{AB}{MN}$ .

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{BC}{NP}=\frac{AC}{MP}=\frac{AB}{MN}=\frac{AB+BC+AC}{MN+MP+NP}=\frac{18}{36}=\frac{1}{2}$.

Do đó, ta có:

NP = 2BC = 2 . 7 = 14 cm.

MP = 2AC = 2 . 6 = 12 cm.

MN = 2AB = 2 . 5 = 10 cm.

Vậy ∆ABC ᔕ ∆MNP với tỉ số đồng dạng bằng $\frac{1}{2}$ .

Bài 9.63 trang 68 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có AB = $\sqrt{15}$ cm và AC = 2BC. Tìm độ dài hai cạnh AC, BC sao cho ABC là một tam giác vuông.

Lời giải:

Vì AC = 2BC > BC nên BC không thể là cạnh huyền nếu tam giác ABC vuông hay tam giác ABC không thể vuông tại A.

TH1: Tam giác ABC vuông tại B.

Áp dụng định lý Pythagore ta có:

AB² + BC² = AC²

Suy ra:

15 + BC² = 4BC²

3BC² = 15

BC² = 5

BC = $\sqrt{5}$ (cm)

Do đó, AC = 2$\sqrt{5}$ (cm).

Ngược lại, nếu AB = $\sqrt{15}$ cm; BC = $\sqrt{5}$ cm; AC = 2$\sqrt{5}$ cm thì AB² + BC² = AC² nên theo định lí đảo của định lí Pythagore thì tam giác ABC vuông tại B.

TH2: Tam giác ABC vuông tại C.

Áp dụng định lý Pythagore ta có:

AC² + BC² = AB²

4BC² + BC² = 15

5BC² = 15

BC² = 3

BC = $\sqrt{3}$ (cm)

Do đó, AC = 2$\sqrt{3}$ (cm).

Ngược lại, nếu AB = $\sqrt{15}$ cm; BC = $\sqrt{3}$ cm; AC = 2$\sqrt{3}$ cm thì AC² + BC² = AB² nên theo định lí đảo của định lí Pythagore thì tam giác ABC vuông tại C.

Vậy để tam giác ABC vuông thì hoặc BC = $\sqrt{5}$ cm; AC = 2$\sqrt{5}$ cm hoặc BC = $\sqrt{3}$ cm; AC = 2$\sqrt{3}$ cm.

Bài 9.64 trang 68 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB > AC. Lấy điểm D trên cạnh AB sao cho AC = AD. Qua D kẻ đường thẳng song song với BC và cắt AC tại E. Qua E kẻ đường thẳng song song với CD và cắt AB tại F. Chứng minh rằng:

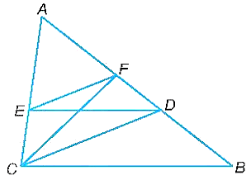
a) AD² = AF . AB.

b) ∆ACF ᔕ ∆ABC.

Chú ý: Đề trong sách cho D thuộc cạnh BC là sai, cần sửa như trên.

Lời giải:

a)

Tam giác ABC có: DE song song với BC nên ∆ADE ᔕ ∆ABC.

Do đó, $\frac{AD}{AB}=\frac{AE}{AC}$ hay AD = $\frac{AB\cdot AE}{AC}$ (1).

Tam giác ADC có: FE song song với DC nên ∆AFE ᔕ ∆ADC.

Do đó, $\frac{AF}{AD}=\frac{AE}{AC}$ , hay AD = $\frac{AF\cdot AC}{AE}$ (2).

Từ (1) và (2) ta có: $A{D}^2=\frac{AB\cdot AE}{AC}\cdot \frac{AF\cdot AC}{AE}=AB\cdot AF$ .

b) Theo câu a có $\frac{AF}{AD}=\frac{AE}{AC}$ và AD = AC (gt), suy ra AE = AF.

Lại có $\frac{AD}{AB}=\frac{AE}{AC}$ nên $\frac{AC}{AB}=\frac{AE}{AD}=\frac{AE}{AC}=\frac{AF}{AC}$ (do AC = AD và AE = AF).

Xét tam giác ACF và tam giác ABC có:

$\widehat{A}$ chung

$\frac{AC}{AB}=\frac{AF}{AC}$ (chứng minh trên)

Do đó, ∆ACF ᔕ ∆ABC (c.g.c).

Bài 9.65 trang 69 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A (AC > AB), có AD là đường phân giác của góc A (D thuộc BC). Qua D vẽ đường thẳng vuông góc với BC cắt cạnh AC tại E và cắt tia BA tại F. Chứng minh rằng:

a) ∆BDF ᔕ ∆EDC;

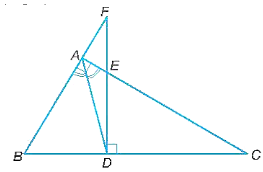
b) BD = DE.

Lời giải:

a)

Tam giác FBD và tam giác CED cùng vuông tại D có:

$\widehat{F}=\widehat{C}\left(=90°-\widehat{B}\right)$.

Do đó, ∆BDF ᔕ ∆EDC (góc nhọn).

b)

Tam giác ABC vuông tại A và tam giác DEC vuông tại D có:

$\widehat{C}$ chung

Do đó, ∆ABC ᔕ ∆DEC (góc nhọn). Suy ra $\frac{AB}{DE}=\frac{AC}{DC}$ .

Vì AD là phân giác của góc BAC trong tam giác ABC nên $\frac{BD}{DC}=\frac{AB}{AC}$ .

Suy ra $\frac{AC}{DC}=\frac{AB}{BD}$ .

Do đó $\frac{AB}{DE}=\frac{AB}{BD}$ . Suy ra BD = DE.

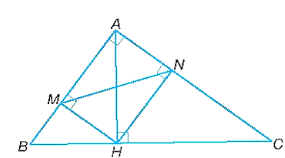
Bài 9.66 trang 69 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH.

a) Biết AB = 3 cm, AC = 4 cm, hãy tính độ dài các đoạn thẳng AH, BH, CH.

b) Gọi M, N lần lượt là chân các đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng ∆HMN ᔕ ∆ABC.

Lời giải:

a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 3² + 4² = 25 nên BC = 5 cm.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AC}{HC}=\frac{BC}{AC}$ nên $CH=\frac{C{A}^2}{CB}=\frac{4^2}{5}=\frac{16}{5}$ (cm).

Do đó, BH = BC – CH = 5 – $\frac{16}{5}$ = $\frac{9}{5}$ (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên $\frac{AB}{HA}=\frac{BC}{AC}$

Do đó, $AH=\frac{AB\cdot AC}{BC}=\frac{3\cdot 4}{5}=\frac{12}{5}$ (cm).

b)

Vì HM vuông góc AB, suy ra $\widehat{HMA}=90°$ .

HN vuông góc với AC, suy ra $\widehat{HNA}=90°$ .

Tứ giác ANHM có: $\widehat{HMA}=\widehat{NAM}=\widehat{HNA}=90{°}_{}$ nên tứ giác ANHM là hình chữ nhật.

Do đó, $\widehat{NHM}=90°$ .

Gọi D là giao điểm của hai đường chéo trong hình chữ nhật NHMA nên DH = DM. Do đó, tam giác DHM cân tại D.

Suy ra: $\widehat{DHM}=\widehat{DMH}$

Lại có: $\widehat{DHM}=\widehat{B}\left(=90°-\widehat{MHB}\right)$ nên $\widehat{DMH}=\widehat{B}$ .

Xét tam giác HMN vuông tại H và tam giác ABC vuông tại A có:

$\widehat{NMH}=\widehat{B}$ (do $\widehat{DMH}=\widehat{B}$ )

Do đó, ∆HMN ᔕ ∆ABC (góc nhọn).

Bài 9.67 trang 69 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:

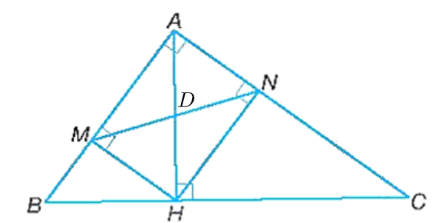
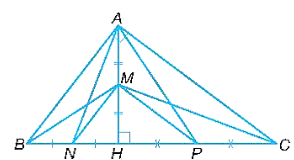
a) ∆MNP ᔕ ∆ABC và tìm tỉ số đồng dạng.

b) ∆ABN ᔕ ∆CAM và ∆ACP ᔕ ∆BAM.

c) AN ⊥ CM và AP ⊥ BM.

Lời giải:

a) Tam giác CAH có P, M lần lượt là trung điểm của CH, AH nên MP là đường trung bình của tam giác ACH, suy ra $\frac{MP}{AC}=\frac{1}{2}$ .

Tam giác BAH có N, M lần lượt là trung điểm của BH, AH nên MN là đường trung bình của tam giác ABH, suy ra $\frac{MN}{AB}=\frac{1}{2}$ .

Ta có $\frac{PN}{CB}=\frac{PH+HN}{CH+HB}=\frac{PH+HN}{2\left(PH+HN\right)}=\frac{1}{2}$ (do N, P lần lượt là trung điểm của HB, HC).

Tam giác MNP và tam giác ABC có:

$\frac{MP}{AC}=\frac{PN}{CB}=\frac{MN}{AB}=\frac{1}{2}$.

Nên ∆MNP ᔕ ∆ABC (c.c.c) với tỉ số đồng dạng bằng $\frac{1}{2}$ .

b)

Tam giác ABH vuông tại H và tam giác HAC vuông tại H có: $\widehat{ABH}=\widehat{CAH}\left(=90°-\widehat{ACH}\right)$

Do đó, ∆HBA ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AB}{AC}=\frac{BH}{AH}=\frac{2BN}{2MA}=\frac{BN}{MA}$ .

Tam giác ABN và tam giác CAM có:

$\widehat{ABN}=\widehat{CAM}$ (cmt)

$\frac{AB}{AC}=\frac{BN}{MA}$ (cmt)

Do đó, ∆ABN ᔕ ∆CAM (c.g.c).

Vì ∆HBA ᔕ ∆HAC (cmt). Suy ra $\frac{AB}{AC}=\frac{AH}{CH}=\frac{2AM}{2CP}=\frac{AM}{CP}$ .

Xét tam giác ACP và tam giác BAM có:

$\widehat{ACP}=\widehat{MAB}\left(=90°-\widehat{CAH}\right)$ (cmt)

Do đó, ∆ACP ᔕ ∆BAM (c.g.c).

c)

+ Vì MN là đường trung bình trong tam giác AHB nên MN song song với AB.

Mà AB vuông góc với AC nên MN vuông góc với AC.

Trong tam giác CAN có MN vuông góc với AC nên MN là đường cao trong tam giác CAN, mà AH là đường cao trong tam giác CAN và M là giao điểm của MN và AH nên M là trực tâm của tam giác CAN. Vậy CM vuông góc với AN.

+ Vì MP là đường trung bình trong tam giác CAH nên MP song song với AC.

Mà AB vuông góc với AC nên MP vuông góc với AB.

Trong tam giác PAB có MP vuông góc với AB nên MP là đường cao trong tam giác PAB, mà AH là đường cao trong tam giác PAB và M là giao điểm của MP và AH nên M là trực tâm của tam giác PAB. Vậy AP vuông góc với BM.

Bài 9.68 trang 69 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB. Chứng minh rằng ∆CAM ᔕ ∆CBN và ∆CHM ᔕ ∆CAN.

Lời giải:

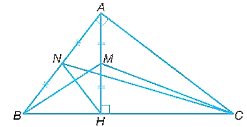
Tam giác ABC vuông tại A và tam giác HAC vuông tại H có: chung.

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{BC}{CA}=\frac{AB}{HA}=\frac{2BN}{2AM}=\frac{BN}{AM}$ (do M, N lần lượt là trung điểm của AH, AB).

Hay $\frac{AC}{CB}=\frac{AM}{BN}$ .

Xét tam giác CAM và tam giác CNB có:

$\widehat{CAM}=\widehat{CBN}\left(=90°-\widehat{BAH}\right)$

$\frac{AC}{CB}=\frac{AM}{BN}$ (cmt)

Do đó, ∆CAM ᔕ ∆CBN (c.g.c).

Vì ∆ABC ᔕ ∆HAC nên ta có: $\frac{AC}{HC}=\frac{AB}{AH}=\frac{2AN}{2HM}=\frac{AN}{HM}$ hay $\frac{HC}{AC}=\frac{HM}{AN}$ .

Xét tam giác CHM vuông tại H và tam giác CAN vuông tại A có:

$\frac{HC}{AC}=\frac{HM}{AN}$ (cmt)

Do đó, ∆CHM ᔕ ∆CAN (hai cạnh góc vuông).

Bài 9.69 trang 69 SBT Toán lớp 8 Tập 2: Vẽ lại Hình 9.18 vào vở và vẽ tứ giác A'B'C'D' là hình đồng dạng phối cảnh của tứ giác ABCD theo tỉ số đồng dạng và tâm phối cảnh là điểm O.

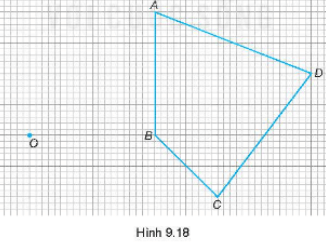
Lời giải:

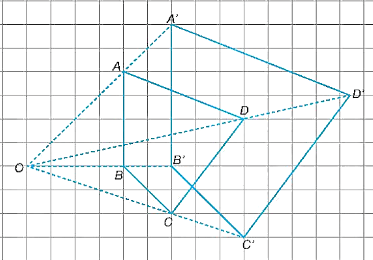
Trên các tia OA, OB, OC, OD lần lượt lấy các điểm A', B', C', D' sao cho

$OA\text{'}=\frac{3}{2}OA;OB\text{'}=\frac{3}{2}OB;OC\text{'}=\frac{3}{2}OC;OD\text{'}=\frac{3}{2}OD$.

Vẽ các đoạn thẳng A'B', C'D', B'C', D'A' ta được tứ giác A'B'C'D' là hình đồng dạng phối cảnh của tứ giác ABCD với tâm phối cảnh là O và tỉ số đồng dạng là $\frac{3}{2}$ .

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Bài 38: Hình chóp tam giác đều

Bài 39: Hình chóp tứ giác đều

Bài tập cuối chương 10