Sách bài tập Toán 8 Bài 36 (Kết nối tri thức): Các trường hợp đồng dạng của hai tam giác vuông

Giải SBT Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 9.42 trang 62 SBT Toán lớp 8 Tập 2: Những điều kiện nào dưới đây kéo theo hai tam giác vuông đồng dạng.

(1) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia.

(2) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia.

(3) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.

(4) Một góc nhọn của tam giác này phụ với một góc nhọn của tam giác kia.

(5) Một cạnh huyền của tam giác này bằng một cạnh huyền của tam giác kia.

(6) Một cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với một cạnh góc vuông và cạnh huyền của tam giác kia.

Lời giải:

Các điều kiện (1), (3), (4), (6) kéo theo hai tam giác vuông đồng dạng.

Giải thích: Các điều kiện (1), (3), (6) là theo các trường hợp bằng nhau của hai tam giác vuông. Điều kiện (4) suy ra một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia (do cùng có tổng với góc nhọn còn lại bằng 90°), vậy quay trở về giống với điều kiện (1).

Bài 9.43 trang 62 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông cân tại A và tam giác MNP có MN = MP = 4 cm và NP = $4\sqrt{2}$ cm. Chứng minh rằng ∆ABC ᔕ ∆MNP.

Lời giải:

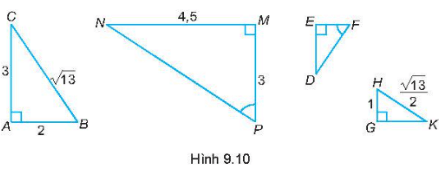
Tam giác ABC vuông cân tại A nên .

Vì MN² + MP² = NP² (do 4² + 4² = ${\left(4\sqrt{2}\right)}^2$)

Nên tam giác MNP vuông tại M (theo định lí Pythagore đảo).

Mà MN = MP = 4 cm nên tam giác MNP vuông cân tại M.

Do đó, $\widehat{N}=45°$ .

Xét tam giác ABC vuông ở A và tam giác MNP vuông ở M có:

$\widehat{B}=\widehat{N}=45°$

Do đó, ∆ABC ᔕ ∆MNP (hai góc nhọn bằng nhau).

Bài 9.44 trang 63 SBT Toán lớp 8 Tập 2: Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng ?

Lời giải:

+) Tam giác ABC vuông ở A và tam giác MPN vuông ở M có:

$\frac{AB}{MP}=\frac{AC}{NM}$$\left(\frac{2}{3}=\frac{3}{4,5}\right)$

Do đó, ∆ABC ᔕ ∆MPN (cặp cạnh góc vuông tỉ lệ).

+) Tam giác MNP vuông tại M và tam giác EDF vuông tại E có:

Do đó, ∆MNP ᔕ ∆EDF (hai góc nhọn bằng nhau).

+) Tam giác ABC vuông ở A và tam giác GHK vuông ở G có:

$\frac{AB}{GH}=\frac{BC}{HK}$$\left(\frac{2}{1}=\frac{\sqrt{13}}{\frac{\sqrt{13}}{2}}\right)$

Do đó, ∆ABC ᔕ ∆GHK (ch – cgv).

Bài 9.45 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:

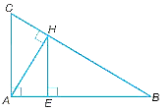
a) ∆ABC ᔕ ∆HAC và CA² = CH . CB.

b) $\frac{AH}{BC}=\frac{HE}{AB}$ .

Lời giải:

a) Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AC}{HC}=\frac{BC}{AC}$ nên AC² = CH . BC.

b)

Vì HE vuông góc với AB (E thuộc AB) nên $\widehat{AEH}=90°$ .

Ta có $\widehat{HAE}+\widehat{CAH}=\widehat{CAB}=90°$ và $\widehat{C}+\widehat{CAH}=90°$ (do tam giác CAH vuông tại H).

Do đó, $\widehat{HAE}=\widehat{C}$ (cùng phụ với góc CAH).

Tam giác AHE vuông ở E và tam giác CBA vuông ở A có:

$\widehat{HAE}=\widehat{C}$

Do đó, ∆AHE ᔕ ∆CBA (hai góc nhọn bằng nhau).

Suy ra: $\frac{AH}{BC}=\frac{HE}{AB}$ .

Bài 9.46 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Lời giải:

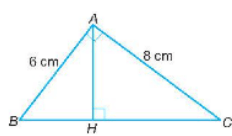
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 6² + 8² = 100

Nên BC = 10 cm.

Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

$\widehat{C}$ chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AC}{HC}=\frac{BC}{AC}$ nên CH = $\frac{C{A}^2}{CB}=\frac{8^2}{10}=\frac{32}{5}=6,4$ (cm).

Do đó, BH = BC – CH = 10 – 6,4 = 3,6 (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên $\frac{AB}{HA}=\frac{BC}{AC}$ .

Do đó, AH = $\frac{AB\cdot AC}{BC}=\frac{6\cdot 8}{10}=4,8$ (cm).

Bài 9.47 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:

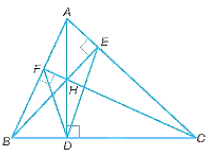
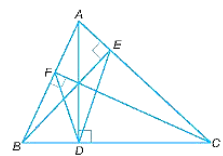
a) HA . HD = HB . HE = HC . HF;

b) ∆AFC ᔕ ∆AEB và AF . AB = AE . AC;

c) ∆BDF ᔕ ∆EDC và DA là tia phân giác của góc EDF.

Lời giải:

a)

Vì AD, BE, CF là các đường cao của tam giác ABC nên AD vuông góc với BC, BE vuông góc với AC, CF vuông góc với AB.

Tam giác AHE vuông ở H và tam giác BHD vuông ở D có:

$\widehat{AHE}=\widehat{BHD}$ (hai góc đối đỉnh)

Do đó, ∆AHE ᔕ ∆BHD (góc nhọn).

Suy ra $\frac{AH}{BH}=\frac{HE}{HD}$ nên HA . HD = HB . HE (1).

Tam giác HBF vuông ở F và tam giác HCE vuông ở E có:

$\widehat{BHF}=\widehat{EHC}$ (hai góc đối đỉnh)

Do đó, ∆HBF ᔕ ∆HCE (góc nhọn).

Suy ra $\frac{HB}{HC}=\frac{HF}{HE}$ nên HB . HE = HC . HF (2).

Từ (1) và (2) ta có: HA . HD = HB . HE = HC . HF.

b)

Tam giác AFC vuông ở F và tam giác AEB vuông ở E có:

$\widehat{BAC}$ chung.c

Do đó, ∆AFC ᔕ ∆AEB (góc nhọn)

Suy ra $\frac{AF}{AE}=\frac{AC}{AB}$ nên AF . AB = AE . AC.

c)

Vì HA . HD = HB . HE nên $\frac{HA}{HE}=\frac{HB}{HD}$

Tam giác HAB và tam giác HED có:

$\frac{HA}{HE}=\frac{HB}{HD}$ (cmt)

$\widehat{AHB}=\widehat{EHD}$ (hai góc đối đỉnh)

Do đó, ∆AHB ᔕ ∆EHD (c.g.c).

Suy ra $\widehat{HAB}=\widehat{HED}$ .

Mà $\widehat{HAB}+\widehat{FBD}=\widehat{HED}+\widehat{DEC}$ (= $90°$ ).

Do đó, $\widehat{FBD}=\widehat{DEC}$.

Chứng minh tương tự ta có: $\widehat{BFD}=\widehat{ECD}$ .

Tam giác BDF và tam giác EDC có:

$\widehat{FBD}=\widehat{DEC}$ (cmt)

$\widehat{BFD}=\widehat{ECD}$ (cmt)

Do đó, ∆BDF ᔕ ∆EDC (g.g).

Suy ra: $\widehat{BDF}=\widehat{EDC}$ .

Mà $\widehat{BDF}+\widehat{FDH}=\widehat{EDC}+\widehat{HDE}\left(=90°\right)$ .

Do đó, $\widehat{FDH}=\widehat{HDE}$ hay $\widehat{FDA}=\widehat{ADE}$ .

Vậy DA là tia phân giác của góc EDF.

Bài 9.48 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:

a) ∆BDF ᔕ ∆BAC và ∆CDE ᔕ ∆CAB;

b) BF . BA + CE . CA = BC².

Lời giải:

Vì AD, BE, CF là các đường cao của tam giác ABC nên AD vuông góc với BC, BE vuông góc với AC, CF vuông góc với AB.

Tam giác BDA vuông ở D và tam giác BFC vuông ở F có:

$\widehat{ABC}$ chung.

Do đó, ∆BDA ᔕ ∆BFC (góc nhọn). Suy ra $\frac{BD}{BF}=\frac{BA}{BC}$ .

Suy ra $\frac{BD}{BA}=\frac{BF}{BC}$ .

Xét tam giác BDF và tam giác BAC có:

$\frac{BD}{BA}=\frac{BF}{BC}$

$\widehat{ABC}$ chung

Do đó, ∆BDF ᔕ ∆BAC (c.g.c).

Tam giác CDA vuông ở D và tam giác CEB vuông ở E có:

$\widehat{ACB}$ chung

Do đó, ∆CDA ᔕ ∆CEB (góc nhọn).

Nên $\frac{CD}{CE}=\frac{CA}{BC}$ .

Suy ra $\frac{CD}{CA}=\frac{CE}{BC}$ .

Tam giác CDE và tam giác CAB có: $\frac{CD}{CA}=\frac{CE}{BC}$

$\widehat{ACB}$ chung

Do đó, ∆CDE ᔕ ∆CAB (c.g.c).

b)

Theo chứng minh phần a ta có:

$\frac{BD}{BA}=\frac{BF}{BC}$ nên BF . BA = BD . BC;

$\frac{CD}{CA}=\frac{CE}{BC}$ nên CE . CA = CD . BC.

Suy ra BF . BA + CE . CA = BD . BC + CD . BC = BC.(BD + CD) = BC . BC = BC².

Vậy BF . BA + CE . CA = BC².

Bài 9.49 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC (M nằm giữa C và H). Kẻ đường thẳng qua M vuông góc với BC lần lượt cắt AC và tia đối của tia AB tại N và P. Chứng minh rằng:

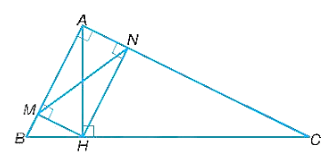
a) ∆ANP ᔕ ∆HBA và ∆MCN ᔕ ∆MPB;

b) $\frac{MB}{MC}\cdot \frac{NC}{NA}\cdot \frac{PA}{PB}=1$

Lời giải:

a) Vì tam giác ABC vuông tại A nên $\widehat{BAC}=90°$ .

Mà $\widehat{BAC}+\widehat{PAN}=180°$ (hai góc kề bù)

Do đó, $\widehat{PAN}=90°$ .

Vì MN vuông góc với BC, AH vuông góc với BC nên MN song song với AH hay MP song song với AH.

Do đó, $\widehat{P}=\widehat{HAB}$ (hai góc đồng vị).

Tam giác ANP vuông tại A và tam giác HBA vuông tại H có:

$\widehat{P}=\widehat{HAB}$ (cmt)

Do đó, ∆ANP ᔕ ∆HBA (hai góc nhọn bằng nhau).

Tam giác MCN vuông tại M và tam giác MPB vuông tại M có:

$\widehat{C}=\widehat{P}$ (cùng phụ với góc B).

Do đó, ∆MCN ᔕ ∆MPB (hai góc nhọn bằng nhau).

b)

Ta có: $\frac{MB}{MC}\cdot \frac{NC}{NA}\cdot \frac{PA}{PB}=\frac{MB}{PB}\cdot \frac{NC}{NA}\cdot \frac{PA}{MC}$ .

Tam giác PMB có: PM song song với AH nên theo định lí Thalès ta có:

$\frac{MB}{MH}=\frac{PB}{PA}$ hay $\frac{MB}{PB}=\frac{MH}{PA}$ .

Tam giác AHC có: MN song song với AH nên theo định lí Thales ta có:

$\frac{NC}{NA}=\frac{MC}{MH}$.

Do đó, $\frac{MB}{MC}\cdot \frac{NC}{NA}\cdot \frac{PA}{PB}=\frac{MB}{PB}\cdot \frac{NC}{NA}\cdot \frac{PA}{MC}$$=\frac{MH}{PA}\cdot \frac{MC}{MH}\cdot \frac{PA}{MC}=1$ .

Bài 9.50 trang 64 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD như Hình 9.11. Biết rằng $\widehat{BAD}=\widehat{BDC}=90°$ , AD = 4 cm, BD = 6 cm và BC = 9 cm. Chứng minh rằng BC // AD.

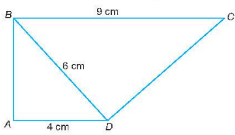
Lời giải:

Tam giác ABD vuông ở A và tam giác DCB vuông ở D (do $\widehat{BAD}=\widehat{BDC}=90°$ ) có:

$\frac{AD}{BD}=\frac{BD}{BC}\left(\frac{4}{6}=\frac{6}{9}\right)$

Do đó, ∆ABD ᔕ ∆DCB (ch – cgv).

Suy ra $\widehat{BDA}=\widehat{DBC}$ .

Mà hai góc này ở vị trí so le trong nên BC // AD.

Bài 9.51 trang 64 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:

a) AM . AB = AH² và AM . AB = AN . AC.

b) ∆AMN ᔕ ∆ACB.

Lời giải:

a) Tam giác AMH vuông ở M và tam giác AHB vuông ở H có:

$\widehat{HAB}$ chung

Do đó, ∆AMH ᔕ ∆AHB (góc nhọn).

Suy ra $\frac{AM}{AH}=\frac{AH}{AB}$ nên AM . AB = AH² (1).

Tam giác ANH vuông ở N và tam giác AHC vuông ở H có:

$\widehat{HAC}$ chung

Do đó, ∆ANH ᔕ ∆AHC (góc nhọn).

Suy ra $\frac{AN}{AH}=\frac{AH}{AC}$ nên AN . AC = AH² (2).

Từ (1) và (2) ta có: AM . AB = AN . AC.

b) Theo phần a ta có: AM . AB = AN . AC nên $\frac{AM}{AC}=\frac{AN}{AB}$ .

Tam giác AMN và tam giác ACB có:

$\widehat{BAC}$ chung $\frac{AM}{AC}=\frac{AN}{AB}$

Do đó, ∆AMN ᔕ ∆ACB (c.g.c).

Bài 9.52 trang 64 SBT Toán lớp 8 Tập 2: Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'. Chứng minh rằng:

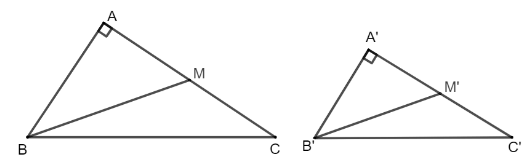
a) BC² + 3BA² = 4BM² và B'C'² + 3B'A'² = 4B'M'²;

b) Nếu $\frac{BC}{BM}=\frac{B\text{'}C\text{'}}{B\text{'}M\text{'}}$ thì ∆ABC ᔕ ∆A'B'C'.

Lời giải:

a) Vì M là trung điểm của AC nên AC = 2AM. Suy ra AC² = (2AM)² = 4AM².

Áp dụng định lý Pythagore cho tam giác ABC vuông tại A có:

BC² = AB² + AC².

Áp dụng định lý Pythagore cho tam giác ABM vuông tại A có:

BM² = AB² + AM².

Do đó, 4BM² = 4(AB² + AM²) = 4AB² + 4AM² = 4AB² + AC²

= 3AB² + (AB² + AC²) = 3AB² + BC².

Vậy BC² + 3BA² = 4BM².

Vì M' là trung điểm của A'C' nên A'C' = 2A'M'. Suy ra A'C'² = (2A'M')² = 4A'M'².

Áp dụng định lí Pythagore cho tam giác A'B'C' vuông tại A' có:

B'C'² = A'B'² + A'C'².

Áp dụng định lý Pythagore cho tam giác A'B'M' vuông tại A' có:

B'M'² = A'B'² + A'M'².

Do đó, 4B'M'² = 4(A'B'² + A'M'²) = 4A'B'² + 4A'M'² = 4A'B'² + A'C'²

= 3A'B'² + (A'B'² + A'C'²) = 3A'B'² + B'C'².

Vậy B'C'² + 3B'A'² = 4B'M'².

b) Giả sử $\frac{BC}{BM}=\frac{B\text{'}C\text{'}}{B\text{'}M\text{'}}$ . Suy ra $\frac{B{C}^2}{B{M}^2}=\frac{B\text{'}C{\text{'}}^2}{B\text{'}M{\text{'}}^2}$ (1).

Theo phần a ta có: BC² + 3BA² = 4BM², chia cả 2 vế cho BM², ta được:

$\frac{B{C}^2}{B{M}^2}+3\frac{B{A}^2}{B{M}^2}=4$.

Tương tự, ta có $\frac{B\text{'}C{\text{'}}^2}{B\text{'}M{\text{'}}^2}+3\frac{B\text{'}A{\text{'}}^2}{B\text{'}M{\text{'}}^2}=4$ .

Do đó, $\frac{B{C}^2}{B{M}^2}+3\frac{B{A}^2}{B{M}^2}=\frac{B\text{'}C{\text{'}}^2}{B\text{'}M{\text{'}}^2}+3\frac{B\text{'}A{\text{'}}^2}{B\text{'}M{\text{'}}^2}\left(=4\right)$ (2).

Từ (1) và (2), suy ra: $\frac{B{A}^2}{B{M}^2}=\frac{B\text{'}A{\text{'}}^2}{B\text{'}M{\text{'}}^2}$ hay $\frac{BA}{BM}=\frac{B\text{'}A\text{'}}{B\text{'}M\text{'}}$ .

Do đó, $\frac{BC}{B\text{'}C\text{'}}=\frac{BM}{B\text{'}M\text{'}}=\frac{BA}{B\text{'}A\text{'}}$.

Hai tam giác ABC vuông tại A và A'B'C' vuông tại A' có $\frac{BC}{B\text{'}C\text{'}}=\frac{BA}{B\text{'}A\text{'}}$ .

Vậy ∆ABC ᔕ ∆A'B'C' (ch – cgv).

Bài 9.53 trang 64 SBT Toán lớp 8 Tập 2: Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.

a) Chứng minh rằng CM ⊥ DN.

b) Biết AB = 4 cm, hãy tính diện tích tam giác ONC.

Lời giải:

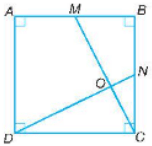
a) Vì ABCD là hình vuông nên AB = BC = CD = DA;

và $\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90°$ .

Vì M là trung điểm của AB nên AM = MB = $\frac{1}{2}$ AB.

Vì N là trung điểm của BC nên NB = NC = $\frac{1}{2}$ BC.

Mà AB = BC nên AM = MB = NB = NC.

Xét tam giác CBM vuông ở B và tam giác DCN vuông ở C có:

MB = NC (cmt)

BC = CD (cmt)

Do đó, tam giác CBM và tam giác DCN bằng nhau (hai cạnh góc vuông).

Suy ra $\widehat{BMC}=\widehat{DNC}$ .

Mà $\widehat{BMC}+\widehat{MCB}=90°$ nên $\widehat{DNC}+\widehat{MCB}=90°$ .

Tam giác CON có:

$\widehat{ONC}+\widehat{OCN}=90°$ (do $\widehat{DNC}+\widehat{MCB}=90°$ ).

Nên $\widehat{NOC}=90°$ .

Do đó, CM vuông góc với DN tại O.

b) Ta có BC = CD = DA = AB = 4 cm; NC = $\frac{1}{2}$ BC = $\frac{1}{2}$ CD = 2 cm hay CD = 2NC.

Áp dụng định lý Pythagore vào tam giác CND vuông tại C ta có:

ND² = NC² + CD² = NC² + (2NC)² = 5NC².

Do đó, $\frac{N{C}^2}{N{D}^2}=\frac{1}{5}$ . Suy ra $\frac{NC}{ND}=\frac{1}{\sqrt{5}}$ .

Xét tam giác NOC vuông tại O và tam giác CND vuông tại C có:

$\widehat{ONC}$ chung

Do đó, ∆ONC ᔕ ∆CND (góc nhọn).

Suy ra $\frac{ON}{CN}=\frac{OC}{CD}=\frac{NC}{ND}=\frac{1}{\sqrt{5}}$ . Do đó, OC = $\frac{1}{\sqrt{5}}$ CD; ON = CN.

Vậy diện tích tam giác ONC là:

$S=\frac{1}{2}OC\cdot ON=\frac{1}{2}.\frac{1}{\sqrt{5}}CD\cdot \frac{1}{\sqrt{5}}CN=\frac{1}{10}\cdot 4\cdot 2=0,8$ (cm²).

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 37: Hình đồng dạng

Bài tập cuối chương 9

Bài 38: Hình chóp tam giác đều

Bài 39: Hình chóp tứ giác đều

Bài tập cuối chương 10