Nội dung bài viết

    Xem thêm

    Bài 6 trang 76 Toán 7 Tập 2 | Chân trời sáng tạo Giải Toán lớp 7

    Lời giải Bài 6 trang 76 Toán 7 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 505 28/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 Chân trời sáng tạo Bài 7: Tính chất ba đường trung tuyến của tam giác 

    Bài 6 trang 76 Toán 7 Tập 2:

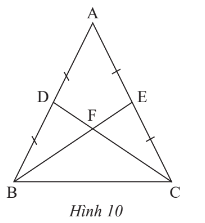
    Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.

    Giải Toán 7 Bài 7 (Chân trời sáng tạo): Tính chất ba đường trung tuyến của tam giác (ảnh 1) 

    Lời giải:

    Ta có BE và CD là hai đường trung tuyến của tam giác ABC nên E và D lần lượt là trung điểm của AC, AB.

    Suy ra AE = 12AC; AD = 12AB.

    Mà AB = AC (do ∆ABC cân tại A) nên AE = AD.

    Xét ∆ABE và ∆ACD có:

    AB = AC (chứng minh trên);

    A^ là góc chung;

    AE = AD (chứng minh trên).

    Do đó ∆ABE = ∆ACD (c.g.c).

    Suy ra BE = CD (hai cạnh tương ứng).

    Ta có F là giao điểm hai đường trung tuyến BE và CD trong ∆ABC nên F là trọng tâm của ∆ABC.

    Do đó DF = 13CD = 13BE = 13. 9 = 3 (cm).

    Vậy DF = 3 cm.

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Khởi động trang 73 Toán 7 Tập 2: Đặt đầu bút chì ở điểm nào của tam giác thì ta có thể giữ tấm bìa thăng bằng...

    Khám phá 1 trang 73 Toán 7 Tập 2: Vẽ tam giác ABC, xác định trung điểm D của cạnh BC và vẽ đoạn thẳng nối hai điểm A và D...

    Thực hành 1 trang 73 Toán 7 Tập 2: Em hãy vẽ tiếp các đường trung tuyến còn lại của tam giác ABC (Hình 1)...

    Vận dụng 1 trang 73 Toán 7 Tập 2: a) Vẽ đường trung tuyến DH của tam giác DEF (Hình 2).b) Vẽ đường trung tuyến MK của tam giác vuông MNP (Hình 3)...

    Khám phá 2 trang 74 Toán 7 Tập 2: a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này...

    Thực hành 2 trang 75 Toán 7 Tập 2: Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM...

    Vận dụng 2 trang 75 Toán 7 Tập 2: Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD...

    Bài 1 trang 75 Toán 7 Tập 2: Quan sát Hình 8. Thay  bằng số thích hợp.EG = EM; GM = EM; GM = EG...

    Bài 2 trang 75 Toán 7 Tập 2: Quan sát Hình 9.a) Biết AM = 15 cm, tính AG. b) Biết GN = 6 cm, tính CN...

    Bài 3 trang 75 Toán 7 Tập 2: Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG...

    Bài 4 trang 75 Toán 7 Tập 2: Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.a) Chứng minh rằng BM = CN...

    Bài 5 trang 76 Toán 7 Tập 2: Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân...

    Bài 6 trang 76 Toán 7 Tập 2: Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm...

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 6: Tính chất ba đường trung trực của tam giác

    Bài 7: Tính chất ba đường trung tuyến của tam giác

    Bài 8: Tính chất ba đường cao của tam giác

    Bài 9: Tính chất ba đường phân giác của tam giác

    Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 505 28/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: