Nội dung bài viết

    Xem thêm

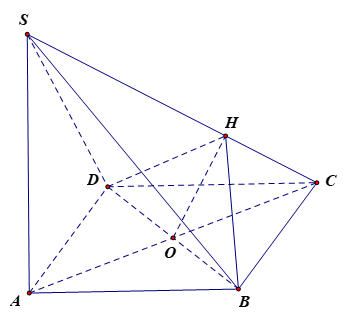
    Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng a, góc BAD bằng 60 độ

    Lời giải Bài 7.21 trang 34 SBT Toán 11 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 9,433 10/12/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 25: Hai mặt phẳng vuông góc

    Bài 7.21 trang 34 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng a, góc BAD bằng 60°. Kẻ OH vuông góc với SC tại H. Biết SA ⊥ (ABCD) và SA = a62 . Chứng minh rằng:

    a) (SBD) ⊥ (SAC);

    b) (SBC)⊥ (BDH);

    c) (SBC) ⊥ (SCD).

    Lời giải:

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng a

    a) Ta có SA ⊥ (ABCD) nên SA ⊥ BD mà BD ⊥ AC (do ABCD là hình thoi).

    Do đó BD ⊥ (SAC) mà BD ⊂ (SBD) nên (SBD) ⊥ (SAC).

    b) Vì BD ⊥ (SAC) nên BD ⊥ SC, mà SC ⊥ OH nên SC ⊥ (BDH).

    Vì SC ⊂ (SBC) nên (SBC)⊥ (BDH).

    c) Ta có tam giác ABD có AB = AD = a và BAD^ = 60o nên tam giác ABD đều.

    Suy ra BD = AB = AD = a.

    Vì ABCD là hình thoi nên AC là tia phân giác của BAD^ mà BAD^ = 60o nên DAO^ = 30o.

    Xét tam giác ADO vuông tại O, có AO = AD . cos30° = a32 . Do đó AC = a3.

    Xét tam giác SAC vuông tại A, có SC = SA2+AC2=6a24+3a2=3a22 .

    Vì ∆CHO đồng dạng ∆CAS (g.g) nên HOAS=COCS⇒CO.ASCS=a2=BD2 .

    Do đó, tam giác BDH vuông tại H, suy ra BHD^ = 90o.

    Mà BH ⊥ SC, DH ⊥ SC (do SC ⊥ (BDH)) và (SBC) ∩ (SCD) = SC,

    BH ⊂ (SBC), DH ⊂ (SCD).

    Do đó góc giữa hai mặt phẳng (SBC) và (SCD) là góc giữa hai đường thẳng BH và DH. Mà (DH, BH) = BHD^ = 90o.

    Vậy (SBC) ⊥ (SCD).

    *Phương pháp giải:

    - Định lí 1.

    Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

    *Lý thuyết:

    1. Định nghĩa.

    Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông.

    Nếu hai mặt phẳng (α) và (β) vuông góc với nhau ta kí hiệu: (α)⊥(β).

    2. Các định lí.

    - Định lí 1.

    Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

    - Hệ quả 1.

    Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.

    - Hệ quả 2.

    Cho hai mặt phẳng (α) và (β) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng (α) ta dựng một đường thẳng vuông góc với mặt phẳng (β) thì đường thẳng này nằm trong mặt phẳng (α).

    Xem thêm

    Chuyên đề Hai mặt phẳng vuông góc () - Toán 1

    TOP 40 câu Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án ) – Toán 11

    Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

    Bài 7.19 trang 34 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD có độ dài các cạnh bằng a. Gọi M là trung điểm của CD...

    Bài 7.20 trang 34 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AC = BC, AD = BD. Gọi M là trung điểm của AB....

    Bài 7.21 trang 34 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O,...

    Bài 7.22 trang 34 SBT Toán 11 Tập 2: Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a. Tính côsin góc giữa hai mặt phẳng sau:...

    Bài 7.23 trang 34 SBT Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a....

    Bài 7.24 trang 34 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,...

    Bài 7.25 trang 35 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD...

    Bài 7.26 trang 35 SBT Toán 11 Tập 2: Một viên bi được thả lăn trên một mặt phẳng nằm nghiêng...

    Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

    Bài 26: Khoảng cách

    Bài 27: Thể tích

    Bài tập cuối chương 7

    Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập

    Bài 29: Công thức cộng xác suất

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 9,433 10/12/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: