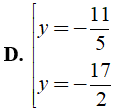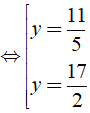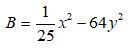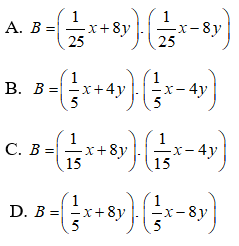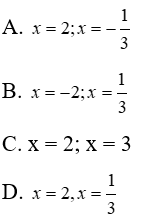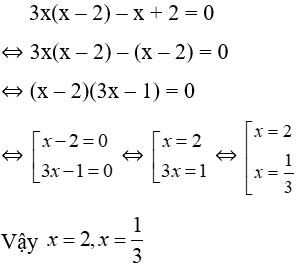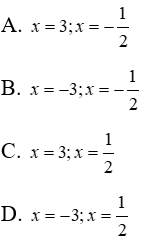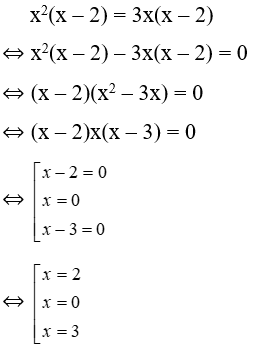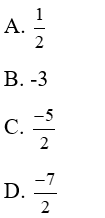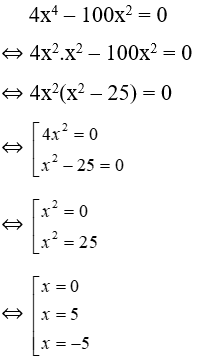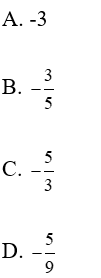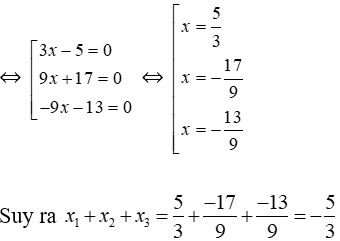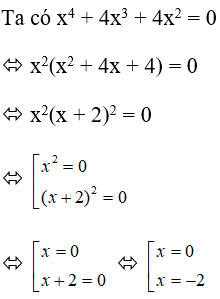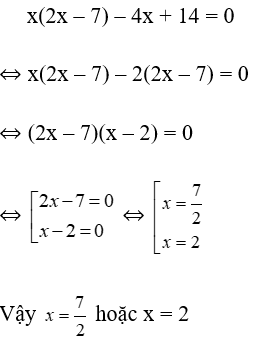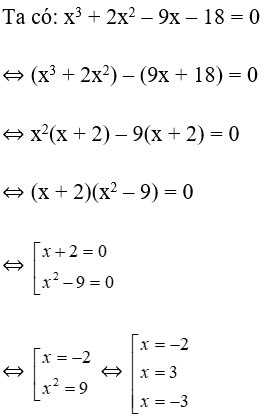50 Bài tập Phân tích đa thức thành nhân tử Toán 8 mới nhất

Bài tập Phân tích đa thức thành nhân tử 

I. Bài tập trắc nghiệm

Bài 1: Đa thức 4x( 2y - z ) + 7y( z - 2y ) được phân tích thành nhân tử là ?

A. ( 2y + z )( 4x + 7y )

B. ( 2y - z )( 4x - 7y )

C. ( 2y + z )( 4x - 7y )

D. ( 2y - z )( 4x + 7y )

Lời giải:

Ta có 4x( 2y - z ) + 7y( z - 2y ) = 4x( 2y - z ) - 7y( 2y - z ) = ( 2y - z )( 4x - 7y ).

Chọn đáp án B.

Bài 2: Đa thức x³( x² - 1 ) - ( x² - 1 ) được phân tích thành nhân tử là ?

A. ( x - 1 )²( x + 1 )( x² + x + 1 )

B. ( x³ - 1 )( x² - 1 )

C. ( x - 1 )( x + 1 )( x² + x + 1 )

D. ( x - 1 )²( x + 1 )( x² + x + 1 )

Lời giải:

Ta có x³( x² - 1 ) - ( x² - 1 ) = ( x² - 1 )( x³ - 1 ) = ( x - 1 )( x + 1 )( x - 1 )( x² + x + 1 )

= ( x - 1 )²( x + 1 )( x² + x + 1 )

Chọn đáp án D.

Sai lầm: Nhiều em học sinh mắc phải sai lầm là nhóm nhân tử ( x² - 1 )( x³ - 1 ) mà không nhận ra trong hai đa thức ( x² - 1 ) và ( x³ - 1 ) có nhân tử chung là ( x - 1 ) để đặt làm nhân tử chung. Dẫn đến nhiều em sẽ chọn đáp án B.

Bài 3: Tìm giá trị y thỏa mãn 49( y - 4 )² - 9( y + 2 )² = 0 ?

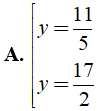
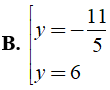
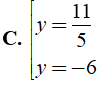
Lời giải:

Ta có 49( y - 4 )² - 9( y + 2 )² = 0

⇔ 49( y² - 8y + 16 ) - 9( y² + 4y + 4 ) = 0

⇔ 49y² - 392y + 784 - 9y² - 36y - 36 = 0

⇔ 40y² - 428y + 748 = 0 ⇔ 4(10y² - 107y + 187 ) = 0

⇔ 4[( 10y² - 22y ) - ( 85y - 187 ) ] = 0 ⇔ 4[ 2y( 5y - 11 ) - 17( 5y - 11 ) ] = 0

⇔ 4( 5y - 11 )( 2y - 17 ) = 0

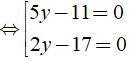
Chọn đáp án A.

Bài 4: Tính giá trị của biểu thức A = x² - y² + 2y - 1 với x=3 và y=1.

A. A = - 9.

B. A = 0.

C. A = 9.

D. A = - 1.

Lời giải:

Ta có A = x² - y² + 2y - 1 = x² - ( y2 - 2y + 1 )

= x² - ( y - 1 )2 

= ( x - y + 1 )( x + y - 1 ) (hằng đẳng thức a² - b² = ( a - b )( a + b ).

Khi đó với x = 3 và y = 1, ta có A = ( 3 - 1 + 1 )( 3 + 1 - 1 ) = 3.3 = 9.

Chọn đáp án C.

Bài 5: Phân tích đa thức thành nhân tử: x³ + x² + y³ + xy

A. (x + y).(x² - xy + y² + x)

B. (x - y).(x² + xy + y² - x)

C. (x + y).(x² + xy + y² - x)

D. (x - y).(x² + xy - y² + x)

Lời giải:

Ta có: x³ + x² + y³ + xy

= (x³ + y³) + (x² + xy)

= (x + y). (x² – xy + y²) + x.(x + y)

= (x + y). (x² - xy + y² + x)

Chọn đáp án A

Bài 6: Phân tích đa thức thành nhân tử: x³ – 9x + 2x²y + xy²

A. x. (x - y + 3).(x + y - 3)

B. x. (x + y + 3).(x + y - 3)

C. x. (x - y + 3).(x - y - 1)

D. x. (x + y + 1).(x - y - 3)

Lời giải:

Ta có: x³ – 9x + 2x²y + xy²

= x.(x² – 9 + 2xy + y²)

= x.[(x² + 2xy + y²) – 9]

= x.[(x + y)² – 32]

= x.(x + y + 3).(x + y - 3)

Chọn đáp án B

Bài 7: Phân tích đa thức thành nhân tử: x⁵ + 4x

A. x.(x² + 2 ).(x² - 2).

B. x.(x² + 2 + x).(x² + 2- x).

C. x.(x² + 2 + 2x).(x² + 2 - 2x).

D. x.(x⁴ + 4)

Lời giải:

Ta có:x⁵ + 4x = x.(x⁴ + 4)

= x.[(x⁴ + 4x² + 4) - 4x²].

= x.[(x² + 2)² - (2x)²].

= x.(x² + 2 + 2x).(x² + 2 - 2x).

Chọn đáp án C

Bài 8: Phân tích đa thức thành nhân tử A = x² – 5x + 4

A. (x - 4).(x - 1)

B. (x – 4).(x + 1)

C. (x + 4).(x + 1)

D. Đáp án khác

Lời giải:

Ta có:A = x² – 5x + 4

= x² – x - 4x + 4A

= (x² – x ) – (4x – 4)A

= x(x – 1) - 4(x – 1)A

= (x - 4). (x – 1)

Chọn đáp án A

Bài 9: Phân tích đa thức thành nhân tử:

Lời giải:

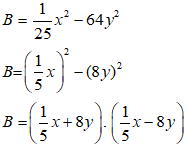Chọn đáp án D

Bài 10: Phân tích đa thức thành nhân tử: 2x²y + 2x + 4xy + x² + 2y + 1

A. (x + 1)². (2y + 1).

B. (x - 1)². (2y - 1).

C. (x² + x + 1). (2y + 1).

D. Đáp án khác

Lời giải:

Ta có:

2x²y + 2x + 4xy + x² + 2y + 1

= (2x²y + 4xy + 2y ) + (x² + 2x + 1 )

= 2y.(x² + 2x + 1) + (x² + 2x + 1)

= 2y(x + 1)² + (x + 1)²

= (x + 1)². (2y + 1).

Chọn đáp án A

Bài tập Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Bài 11: Tìm nhân tử chung của biểu thức 5x²(5 – 2x) + 4x – 10 có thể là

A. 5 – 2x    

B. 5 + 2x    

C. 4x – 10  

D. 4x + 10

Lời giải:

Ta có 5x²(5 – 2x) + 4x – 10

= 5x²(5 – 2x) – 2(-2x + 5)                                     

= 5x²(5 – 2x) – 2(5 – 2x)

Nhân tử chung là 5 – 2x

Đáp án cần chọn là: A

Bài 12: Nhân tử chung của biểu thức 30(4 – 2x)² + 3x – 6 có thể là

A. x + 2      

B. 3(x – 2)  

C. (x – 2)²   

D. (x + 2)²

Lời giải:

Ta có:

30(4 – 2x)² + 3x – 6

= 30(2x – 4)² + 3(x – 2)

= 30.2²(x – 2) + 3(x – 2)

= 120(x – 2)² + 3(x – 2)

= 3(x – 2)(40(x – 2) + 1) = 3(x – 2)(40x – 79)

Nhân tử chung có thể là 3(x – 2)

Đáp án cần chọn là: B

Bài 13: Tìm giá trị x thỏa mãn 3x(x – 2) – x + 2 = 0

Lời giải:

Ta có:

Đáp án cần chọn là: D

Bài 14: Tìm giá trị x thỏa mãn 2x(x – 3) – (3 – x) = 0

Lời giải:

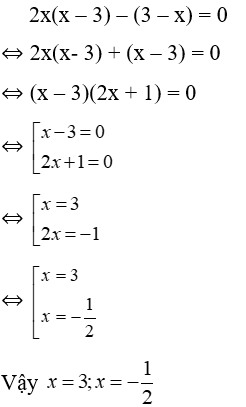
Bài 15: Có bao nhiêu giá trị x thỏa mãn 5(2x – 5) = x(2x – 5)

A. 1            

B. 2            

C. 3            

D. 0

Lời giải:

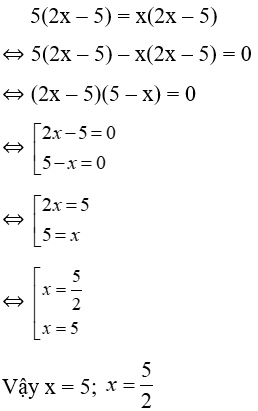
Bài 16: Có bao nhiêu giá trị x thỏa mãn x²(x – 2) = 3x(x – 2)

A. 1            

B. 2            

C. 3            

D. 0

Lời giải:

Ta có:

Vậy có 3 giá trị x thỏa mãn điều kiện đề bài x = 2; x = 0; x = 3.

Đáp án cần chọn là: C

Bài 17: Cho x₁ và x₂ là hai giá trị thỏa mãn x(5 – 10x) – 3(10x – 5) = 0. Khi đo x₁ + x₂ bằng

Lời giải:

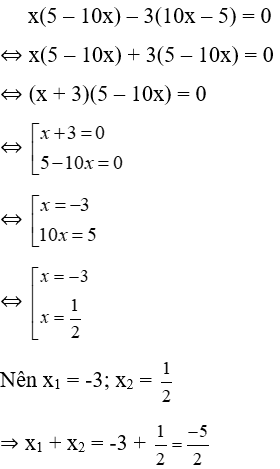
Bài 18: Cho x₁ và x₂ (x₁ > x₂) là hai giá trị thỏa mãn x(3x – 1) – 5(1 – 3x) = 0. Khi đó 3x₁ – x₂ bằng:

A. -4          

B. 4            

C. 6             

D. -6

Lời giải:

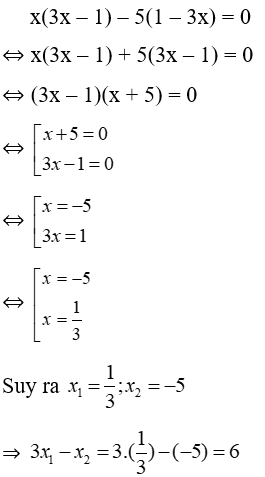
Bài 19: Cho x₀ là giá trị lớn nhất thỏa mãn 4x⁴ – 100x² = 0. Chọn câu đúng.

A. x₀ < 2     

B. x₀ < 0     

C.x₀ > 3      

D. 1 < x₀ < 5

Lời giải:

Ta có:

Do đó x0 = 5 ⇒ x0 > 3

Đáp án cần chọn là: C

Bài 20: Cho x₀ là giá trị lớn nhất thỏa mãn 25x⁴ – x² = 0. Chọn câu đúng.

A. x₀ < 1     

B. x₀ = 0     

C. x₀ > 3     

D. 1 < x₀ < 2

Lời giải:

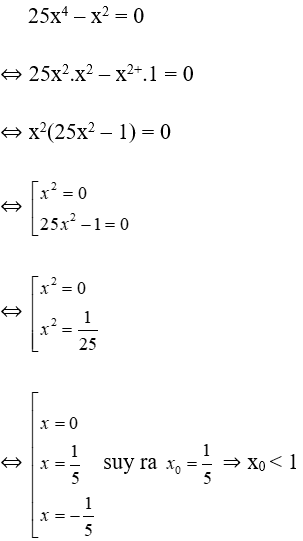
Bài 21: Gọi x₁; x₂; x₃ là các giá trị thỏa mãn 4(3x – 5)² – 9(9x² – 25)² = 0. Khi đó x₁ + x₂ + x₃ bằng

Lời giải:

Ta có 4(3x – 5)² – 9(9x2 – 25)² = 0

⇔ 4(3x – 5)² – 9[(3x)2 – 52]² = 0

⇔ 4(3x – 5)² – 9[(3x – 5)(3x + 5)]² = 0

⇔ 4(3x – 5)² – 9(3x – 5)2(3x + 5)² = 0

⇔ (3x – 5)²[4 – 9(3x + 5)²] = 0

⇔ (3x – 5)²[4 – (3(3x + 5))²] = 0

⇔ (3x – 5)²(22 – (9x + 15)²) = 0

⇔ (3x – 5)²(2 + 9x + 15)(2 – 9x – 15) = 0

⇔ (3x – 5)²(9x + 17)(-9x – 13) = 0

Đáp án cần chọn là: C

Bài 22: Cho các phương trình (x + 2)³ + (x – 3)³ = 0 (1) ; (x² + x – 1)² + 4x² + 4x = 0 (2). Chọn câu đúng

A. Phương trình (1) có hai nghiệm, phương trình (2) vô nghiệm

B. Phương trình (1) có 1 nghiệm, phương trình (2) có 2 nghiệm

C. Phương trình (1) vô nghiệm, phương trình (2) vô nghiệm

D. Phương trình (1) có 1 nghiệm, phương trình (2) vô nghiêm

Lời giải:

Xét phương trình (1) ta có:

 

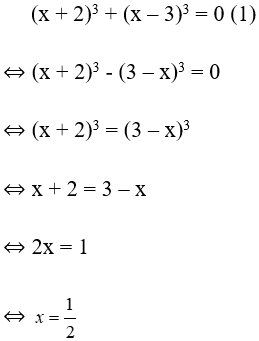
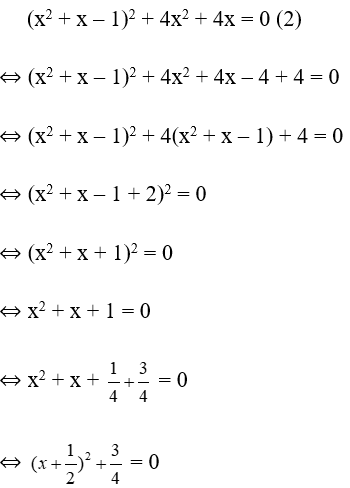
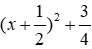Vì  > 0, Ɐx nên phương trình (2) vô nghiệm

Bài 23: Cho x + n = 2(y – m), khi đó giá trị của biểu thức A = x² – 4xy + 4y² – 4m² – 4mn – n² bằng

A. A = 1     

B. A = 0     

C. A = 2     

D. Chưa đủ dữ kiện để tính

Lời giải:

Ta có:

A = x² – 4xy + 4y² – 4m² – 4mn – n²

= x² – 2x.2y + (2y)² – (4m² + 4mn + n²)

= (x – 2y)² – (2m + n)²

= (x – 2y + 2m + n)(x – 2y – 2m – n)

Ta có:

x + n = 2(y – m) ⇔ x + n = 2y – 2m

⇔ x + n = 2y – 2m

⇔ x – 2y +n + 2m = 0

Thay x – 2y + n + 2m = 0 vào A ta được

A = 0.(x – 2y – 2m – n) = 0

Vậy A = 0

Đáp án cần chọn là: B

Bài 24: Cho x – 4 = -2y. Khi đó giá trị của biểu thức M = (x + 2y – 3)² – 4(x + 2y – 3) + 4 bằng

A. M = 0    

B. M = -1   

C. M = 1     

D. Đáp án khác

Lời giải:

Ta có: M = (x + 2y – 3)² – 4(x + 2y – 3) + 4         

= (x + 2y – 3)² – 2(x + 2y – 3).2 + 22         

= (x + 2y – 3 – 2)² = (x + 2y – 5)²

Ta có: x – 4 = -2y ⇔ x + 2y = 4

Thay x + 2y = 4 vào M ta được:

M = (4 – 5)² = (-1)²

Vậy M = 1

Đáp án cần chọn là: C

Bài 25: Cho 9a² – (a – 3b)² = (m.a + n.b)(4a – 3b) với m, n Є R. Khi đó, giá trị của m và n là

A. m = -2; n = -3

B. m = 3; n = 2

C. m = 3; n = -4

D. m = 2; n = 3

Lời giải:

Ta có: 9a² – (a – 3b)² = (3a)² – (a – 3b)² 

= (3a + a – 3b)(3a – a + 3b)                            

= (4a – 3b)(2a + 2b)

Suy ra m = 2; n = 3

Đáp án cần chọn là: D

Bài 26: Đa thức 4b²c² – (c² + b² – a²)² được phân tích thành

A. (b + c + a)(b + c – a)(a + b – c)(a – b + c)

B. (b + c + a)(b – c – a)(a + b – c)(a – b + c)

C. (b + c + a)(b + c – a)(a + b – c)²

D. (b + c + a)(b + c – a)(a + b – c)(a – b – c)

Lời giải:

Ta có 4b²c² – (c² + b² – a²)²         

= (2bc)² – (c2 + b2 – a2)²         

= (2bc + c² + b² – a²)(2bc – c² – b² + a²)         

= [(b + c)² – a²][a² – (b² – 2bc + c²)]         

= [(b + c)² – a²][a² – (b – c)²]         

= (b + c + a)(b + c – a)(a + b – c)(a – b + c)

Đáp án cần chọn là: A

Bài 27: Đa thức x⁶ – y⁶ được phân tích thành

A. (x + y)²(x² – xy + y²)(x² + xy + y²)

B. (x + y)(x² – 2xy + y²)(x – y)(x² + 2xy + y²)

C. (x + y)(x² – xy + y²)(x – y)(x² + xy + y²)

D. (x + y)(x² + 2xy + y²)(y – x)(x² + xy + y²)

Lời giải:

Ta có

x⁶ – y⁶ = (x³)² – (y³)² = (x³ + y³)(x³ – y³)

= (x + y)(x² – xy + y²)(x – y)(x² + xy + y²)

Đáp án cần chọn là: C

Bài 28: Tính giá trị biểu thức P = x³ – 3x² + 3x với x = 101

A. 100³+ 1  

B. 100³ – 1 

C. 100³       

D. 101³

Lời giải:

Ta có

P = x³ – 3x² + 3x – 1 + 1 = (x – 1)³ + 1

Thay x = 101 vào P ta được:

P = (101 – 1)³ + 1 = 1003 + 1

Đáp án cần chọn là: A

Bài 29: Hiệu bình phương các số lẻ liên tiếp thì luôn chia hết cho

A. 8            

B. 9            

C. 10          

D. Cả A, B, C đều sai

Lời giải:

Gọi hai số lẻ liên tiếp là 2k – 1; 2k + 1 (k Є N*)

Theo bài ra ta có:

(2k + 1)² – (2k – 1)² 

= 4k² + 4k + 1 – 4k² + 4k – 1 = 8k ⁝ 8

Đáp án cần chọn là: A

Bài 30: Có bao nhiêu cặp số nguyên (x; y) thỏa mãn x² + 102 = y²

A. 0            

B. 1            

C. 2            

D. 3

Lời giải:

Ta có x² + 102 = y² 

⇔ y² – x² = 102

Nhận thấy hiệu hai bình phương là một số chẵn nên x, y cùng là số chẵn hoặc cùng là số lẻ

Suy ra y – x; y + x luôn là số chẵn

Lại có y² – x² = 102 ⇔ (y – x)(y + x) = 102

Mà (y – x) và (y + x) cùng là số chẵn.

Suy ra (y – x)(y + x) chia hết cho 4 mà 102 không chia hết cho 4 nên không tồn tại cặp số x; y thỏa mãn đề bài

Đáp án cần chọn là: A

Bài 31: Cho ax² – 5x² – ax + 5x + a – 5 = (a + m)(x² – x + n) với với m, n Є R. Tìm m và n

A. m = 5; n = -1

B. m = -5; n = -1

C. m = 5; n = 1

D. m = -5; n = 1

Lời giải:Ta có

ax² – 5x² – ax + 5x + a – 5

= x²(a – 5) – x(a – 5) + a – 5

= (a – 5)(x² – x + 1)

Suy ra m = -5; n = 1

Đáp án cần chọn là: D

Bài 32: Cho x² – 4y² – 2x – 4y = (x + 2y)(x – 2y + m) với m Є R. Chọn câu đúng

A. m < 0     

B. 1 < m < 3

C. 2 < m < 4

D. m > 4

Lời giải:

Ta có x² – 4y² – 2x – 4y

= (x² – 4y²) – (2x + 4y)

= (x – 2y)(x + 2y) – 2(x + 2y)

= (x + 2y)(x – 2y – 2)

Suy ra m = -2

Đáp án cần chọn là: A

Bài 33: Cho x² – 4xy + 4y² – 4 = (x – my + 2)(x – 2y – 2) với m Є R. Chọn câu đúng

A. m < 0     

B. 1 < m < 3

C. 2 < m < 4

D. m > 4

Lời giải:

Ta có

x² – 4xy + 4y² – 4 = (x² – 2.x.2y + (2y)²) – 4

= (x – 2y)² – 22 = (x – 2y – 2)(x – 2y + 2)

Suy ra m = 2

Đáp án cần chọn là: B

Bài 34: Tìm x biết x⁴ + 4x³ + 4x² = 0

A. x = 2; x = -2

B. x = 0; x = 2

C. x = 0; x = -2

D. x = -2

Lời giải:

Vậy x = 0; x = -2

Đáp án cần chọn là: C

Bài 35: Tìm giá trị của x thỏa mãn x(2x – 7) – 4x + 14 = 0

Lời giải:

Đáp án cần chọn là: C

Bài 36: Có bao nhiêu giá trị của x thỏa mãn x³ + 2x² – 9x – 18 = 0

A. 1           

 B. 2            

C. 0            

D. 3

Lời giải:

Vậy x = -2; x = 3; x =-3

Đáp án cần chọn là: D

Bài 37: Có bao nhiêu giá trị của x thỏa mãn x(x – 1)(x + 1) + x2 – 1 = 0

A. 1           

B. 2           

C. 0           

D. 3

Lời giải:

Ta có:x(x – 1)(x + 1) + x² – 1 = 0

⇔ x(x – 1)(x + 1) + (x2 – 1) = 0

⇔ x(x – 1)(x + 1) + (x – 1)(x + 1) = 0

⇔ (x + 1)(x – 1)(x + 1) = 0

⇔ (x + 1)²(x – 1) = 0

Vậy x = 1; x = -1

Đáp án cần chọn là: B

Bài 38: Cho |x| < 2. Khi đó khẳng định nào sau đây là đúng khi nói về giá trị của biểu thức A = x⁴ + 2x³ – 8x – 16.

A. A > 1     

B. A > 0     

C. A < 0     

D. A ≥ 1

Lời giải:

Ta có A = x⁴ + 2x³ – 8x – 16

= (x⁴ – 16) + (2x³ – 8x)

= (x² – 4)(x² + 4) + 2x(x² – 4)

= (x² – 4)(x² + 2x + 4)

Ta có x² + 2x + 4 = x² + 2x + 1 + 3 = (x + 1)² + 3 ≥ 3 > 0, Ɐx

Mà |x| < 2 ⇔ x² < 4 ⇔ x² – 4 < 0

Suy ra A = (x² – 4)(x² + 2x + 4) < 0 khi |x| < 2

Đáp án cần chọn là: C

Bài 39: Cho x = 10 – y. Khi đó khẳng định nào sau đây là đúng khi nói về giá trị của biểu thức N = x³ + 3x²y + 3xy² + y³ + x² + 2xy + y²

A. N > 1200

B. N < 1000

C. N < 0     

D. N > 1000

Lời giải:

Ta có N = x³ + 3x²y + 3xy² + y³ + x² + 2xy + y²

= (x³ + 3x²y + 3xy² + y³) + (x² + 2xy + y²)

= (x + y)³ + (x + y)² = (x + y)²(x + y + 1)

Từ đề bài x = 10 – y ⇔ x + y = 10.

Thay x + y = 10 vào N = (x + y)²(x + y + 1) ta được

N = 102(10 + 1) = 1100

Suy ra N > 1000 khi x = 10 – y

Đáp án cần chọn là: D

Bài 40: Cho ab³c² – a²b²c³ – a²bc³ = abc²(b + c)(…) Biểu thức thích hợp điền vào dấu … là

A. b – a      

B. a – b      

C. a + b      

D. -a – b

Lời giải:

Ta có ab³c² – a²b²c³ – a²bc³

= abc²(b² – ab + bc – ac)

= abc²[(b² – ab) + (bc – ac)]

= abc²[b(b – a) + c(b – a)]

= abc²(b + c)(b – a)

Vậy ta cần điền b – a

Đáp án cần chọn là: A

II. Bài tập tự luận

Bài 1: Phân tích các đa thức sau thành nhân tử:

a) 3x – 6y;

b) $\frac{2}{5}$ x² + 5x³ + x²y;

Lời giải:a) 3x – 6y = 3 . x – 3 . 2y = 3(x – 2y)

b) $\frac{2}{5}$ x² + 5x³ + x²y = x²($\frac{2}{5}$+ 5x + y)

Bài 2: Tính giá trị biểu thức:

a) 15 . 91,5 + 150 . 0,85;

b) x(x – 1) – y(1 – x) tại x = 2001 và y = 1999.

Lời giải:

a) 15 . 91,5 + 150 . 0,85

= 15 . 91,5 + 15 . 8,5

= 15(91,5 + 8,5)

= 15 . 100 = 1500

b) x(x – 1) – y(1 – x)

= x(x – 1) – y[-(x – 1)]

= x(x – 1) + y(x – 1)

= (x – 1)(x + y)

Tại x = 2001, y = 1999 ta được:

(2001 – 1)(2001 + 1999) = 2000 . 4000

= 8000000

Bài 3: Tìm x, biết:

a) 5x(x -2000) – x + 2000 = 0;

b) x³ – 13x = 0

Lời giải:

a) 5x(x -2000) – x + 2000

= 05x(x -2000) – (x – 2000)

= 0(x – 2000)(5x – 1) = 0

Hoặc 5x – 1 = 0 => 5x = 1 => x =1/5

Vậy x = $\frac{1}{5}$; x = 2000

b) x³ – 13x = 0x(x² – 13) = 0

Hoặc x = 0

Hoặc x² – 13 = 0 => x² = 13 => x = ±$\sqrt{13}$

Vậy x = 0; x = ±$\sqrt{13}$

Bài 4: Tính nhanh:

a, 85.12,7 + 5.3.12,7

b, 52.143 – 52.39 – 8.26

Lời giải:

a, 85.12,7 + 5.3.12,7

= 12,7.(85 + 5.3)

= 12,7.100 = 1270

b, 52.143 – 52.39 – 8.26

= 52.143 – 52.39 – 52.4

= 52.(143 – 39 – 4)

= 52.100 = 5200

Bài 5: Phân tích thành nhân tử:

a, 5x – 20y

b, 5x(x – 1) – 3x(x – 1)

c, x(x + y) – 5x – 5y

Lời giải:

a, 5x – 20y = 5x – 5.4y = 5(x – 4y)

b, 5x(x – 1) – 3x(x – 1) = x(x – 1)(5 – 3) = 2x(x – 1)

c, x(x + y) – 5x – 5y = x(x + y) – 5(x + y) = (x + y)(x – 5)

Bài 6: Tính giá trị của các biểu thức sau:

a, x² + xy + x tại x = 77 và y = 22

b, x(x – y) + y(y – x) tại x= 53 và y =3

Lời giải:

a, Ta có: x² + xy + x = x(x + y + 1)

Thay x = 77, y = 22 vào biểu thức, ta được:

x(x + y + 1) = 77.(77 + 22 + 1) = 77.100 = 7700

b, Ta có: x(x – y) + y(y – x) = x(x – y) – y(x – y) = (x – y)(x – y) = (x – y)²

Thay x = 53, y = 3 vào biểu thức ta được:

(x – y)² = (53 – 3)² = 50² = 2500

Bài 7: Tìm x biết:

a, x + 5x² = 0

b, x + 1 = (x + 1)²

Lời giải:

a, Ta có: x + 5x² = 0

⇔ x(1 + 5x) = 0

⇔ x = 0 hoặc 1 + 5x = 01 + 5x = 0

⇒ x = - 1/5 . Vậy x = 0 hoặc x = - 1/5

b, Ta có: x + 1 = (x + 1)²

⇔ (x + 1)² – (x + 1) = 0

⇔ (x + 1)[(x + 1) – 1] = 0

⇔ (x + 1).x = 0⇔ x = 0 hoặc x + 1 = 0x + 1 = 0 ⇒ x = -1.

Vậy x = 0 hoặc x = -1.

Bài 8: Chứng minh rằng: n² (n + 1) + 2n(n + 1) luôn chia hết cho 6 với mọi số nguyên n.

Lời giải:

Ta có n² (n + 1) + 2n(n + 1)

= n(n + 1)(n + 2)

Vì n và n + 1 là 2 số nguyên liên tiếp nên (n + 1) ⋮ 2n, n + 1,

n + 2 là 3 số nguyên liên tiếp, nên n(n + 1)(n + 2) ⋮ 3 mà ƯCLN (2;3) = 1

vậy n(n + 1)(n + 2) ⋮ (2.3) = 6

Bài 9: Phân tích các đa thức sau thành nhân tử:

a) 14x²y – 21xy² + 28x²y²;

b) $\frac{2}{5}$x(y – 1) – $\frac{2}{5}$y(y – 1);

c) 10x(x – y) – 8y(y – x).

Lời giải:

a) 14x²y – 21xy² + 28x²y² 

= 7xy . 2x – 7xy . 3y + 7xy . 4xy

= 7xy(2x – 3y + 4xy)

b) $\frac{2}{5}$ x(y – 1) – $\frac{2}{5}$y(y – 1)

= $\frac{2}{5}$(y – 1)(x – y)

c) 10x(x – y) – 8y(y – x)

=10x(x – y) – 8y[-(x – y)]

= 10x(x – y) + 8y(x – y)

= 2(x – y)(5x + 4y)

Bài 10: Chứng minh rằng 55^{n + 1} – 55ⁿ chia hết cho 54 (với n là số tự nhiên)

Lời giải: 55^{n + 1} – 55ⁿ chia hết cho 54 (n ∈ N)

Ta có 55^{n + 1} – 55ⁿ = 55ⁿ . 55 – 55ⁿ= 55ⁿ (55 – 1)= 55ⁿ . 54

Vì 54 chia hết cho 54 nên 55n . 54 luôn chia hết cho 54 với n là số tự nhiên.

Vậy 55^{n + 1} – 55ⁿ chia hết cho 54.

III. Bài tập vận dụng

Bài 1: Thực hiện phép chia đa thức sau đây bằng cách phân tích đa thức bị chia thành nhân tử:

a) (x5+ x3+ x2 + 1):(x3 + 1)

b) (x2-5x + 6):(x - 3)

Bài 2: Phân tích các đa thức sau thành nhân tử:

a, 

b, 

Bài 3: Tính giá trị của biểu thức dưới đây, biết : x²  - x - 6 = 0A = x⁴ + 2x³ + 2x² + 2x +1

Bài 4: Tìm x biết:

a, 

b, 

Bài 5: Chứng minh rằng nếu a² + b² = 2ab thì a = b.

Bài 6: Phân tích đa thức x² + x – 6 thành nhân tử ta được kết quả là?

Bài 7: phân tích đa thức thành nhân tử :

a) a²– b² – 2x(a – b)

b) a² – b² – 2x(a + b)

Bài 8: Tìm giá trị lớn nhất của biểu thức :

a) A = -4x² – 12x

b) B = 3 – 4x – x²

c) C = x²  + 2y² + 2xy – 2y

d) D = 2x – 2 – 3x²

Bài 9: Tìm giá trị nhỏ nhất của biểu thức:

a) A = x² – x + 1                                                 

b) B = 4x² + y² – 4x – 2y + 3                                    

c) C = x² + 5x + 8

d) C = x² + x + 1                                                      

e) D = 2x² + 8x + 9